پایستگی انرژی — به زبان ساده

پیش‌تر در بلاگ فرادرس قضیه کار و انرژی را توضیح دادیم. جالب است بدانید قضیه کار و انرژی یکی از حالات خاص قانونی کلی‌تر تحت عنوان قانون پایستگی انرژی است. در این مطلب قصد داریم تا این قانون را به زبان ساده توضیح دهیم.

تعریف قانون پایستگی انرژی

در فیزیک اصطلاح پایستگی به شرایطی اطلاق دارد که در آن یک کمیت با گذشت زمان ثابت بماند. برای نمونه وقتی می‌گوییم جرم پایسته است، یعنی این که با گذشت زمان تغییر نمی‌کند.

در فیزیک کمیت‌های پایسته‌ی بسیاری وجود دارند. در اغلب موارد می‌توان از ثابت بودن این کمیت‌ها به‌ منظور پیش‌بینی رخداد‌های فیزیکی استفاده کرد. در فیزیک سه کمیت اصلی وجود دارد که مقدار آن‌ها با گذشت زمان ثابت است. این کمیت‌ها،‌ انرژی، تکانه و تکانه زاویه‌ای هستند. شکل‌های مختلفی از انرژی هم‌چون انرژی پتانسیل، الکتریکی، گرانشی و گرمایی وجود دارد، اما حاصل جمع آن‌ها مقداری ثابت است. قانون پایستگی انرژی از دو اصل مهم که در ادامه آمده پیروی می‌کند:

فیلم آموزش فیزیک پایه دهم – فیزیک 1

کلیک کنید

• قانون پایستگی انرژی فقط می‌تواند به سیستم‌هایی اطلاق شود که نسبت به محیط اطرافشان ایزوله هستند. برای نمونه توپی که روی سطحی دارای اصطکاک حرکت می‌کند، از قانون پایستگی انرژی پیروی نمی‌کند، چرا که توپ نسبت به سطح ایزوله نشده است. در حقیقت سطحِ مذکور روی توپ کار انجام داده و از آن انرژی می‌گیرد؛ بنابراین انرژی توپ با زمان تغییر کرده و ثابت نخواهد بود.
• انرژی کل یک سیستم ثابت بوده ولی هریک از بخش‌های انرژی هم‌چون انرژی گرانشی، پتانسیل یا حرارتی می‌توانند تغییر کنند.

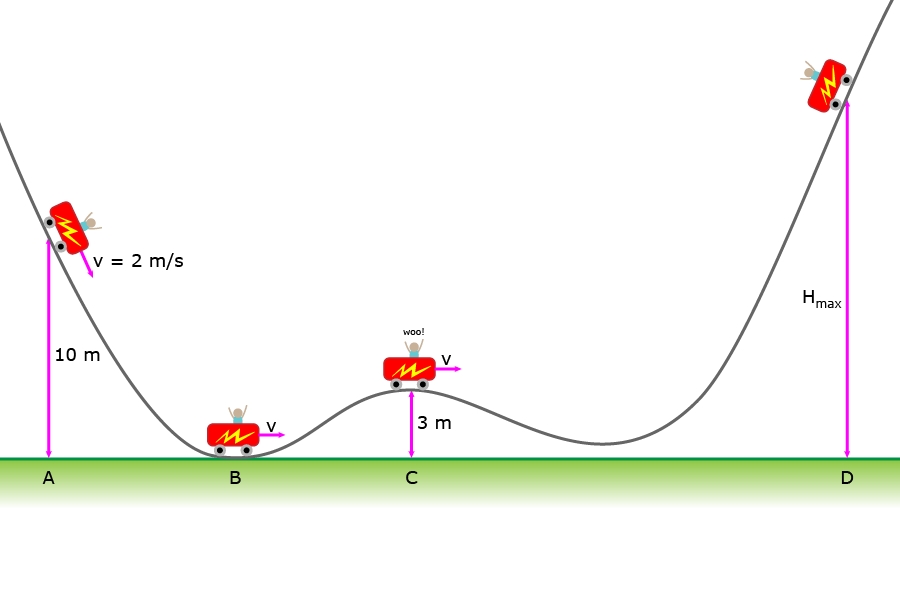
برای نمونه در انیمیشن زیر اگر خودرو را برابر با سیستم در نظر بگیرید، می‌بینید که انرژی کل آن (ستون زرد رنگ) همواره ثابت بوده و تنها انرژی‌های جنبشی (ستون سبز) و پتانسیل در طول مسیر حرکت به هم تبدیل می‌شوند. توجه داشته باشید که ماشین خاموش بوده و رها شده است.

در اکثر مسائل فیزیک که با آن‌ها مواجه خواهید شد، احتمالا بیشتر با انرژی‌های پتانسیل گرانشی، انرژی جنبشی، انرژی ذخیره شده در فنر و انرژی حرارتی مواجه خواهید شد. معمولا به‌منظور حل مسائل مربوط به پایستگی انرژی، انرژی کل سیستم را در حالت ابتدایی و انتهایی یک رخ داد نوشته و با برابر قرار دادن این دو حالت یک کمیت مجهول (مثلا سرعت) بدست می‌آید.

برای نمونه فرض کنید جرمی به فنر متصل شده و در حالت فشرده شده نگه داشته شده است. بدیهی است که قبل از رها کردن جرم، سیستم تنها دارای انرژی پتانسیل است. پس از رها کردن جرم، انرژی پتانسیل ذخیره شده در فنر به انرژی جنبشی تبدیل می‌شود. در نتیجه با برابر قرار دادن انرژی جنبشی و پتانسیل، سرعت جرم در نتیجه کشیده شدن فنر بدست خواهد آمد.

در حالت کلی،‌ مجموع انرژی جنبشی، پتانسیل و کششی یک سیستم جرم و فنر در حالت ابتدا و انتهاییش برابر است با:

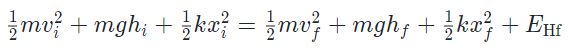
منظور از سیستم چیست؟

در فیزیک، سیستم به مجموعه‌ای از اشیاء گفته می‌شود که اثرات فیزیکی همچون نیرو روی آن‌ها بررسی می‌شود. برای نمونه اگر هدف مدل‌سازی حرکت یک جسم است، در این صورت بایستی خود جسم به عنوان سیستم در نظر گرفته شود.

در عمل، به‌ منظور بررسی یک سیستم بایستی تعدادی از تاثیرات وارد شده به آن نادیده گرفته شوند. معمولا هنگام تعریف سیستم، با استفاده از یک منحنی سیستم انتخاب شده نسبت به محیط اطرافش جدا می‌شود. به اجزائی که در بیرون از منحنی قرار می‌گیرند، محیط گفته می‌شود. توجه داشته باشید که با انتخاب مناسب سیستم و محیط می‌توان محاسبات را راحت‌تر انجام داد.

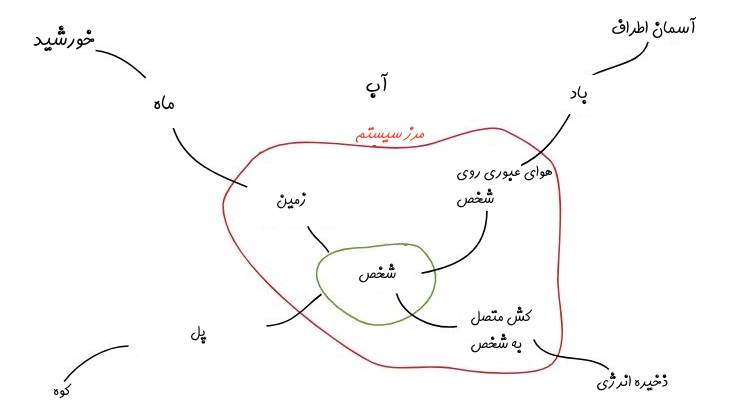
شخصی را تصور کنید که ورزش بانجی جامپینگ را انجام می‌دهد. اگر این شخص از یک پل به پایین بپرد، در پایین‌ترین حالت، سیستم از شخص، زمین و کِش متصل شده به پای شخص تشکیل شده است. اگر بخواهیم مسئله را با دقتی بیشتر حل کنیم، بایستی هوا را نیز به عنوان بخشی از سیستم در نظر بگیریم. در شکل زیر سیستم و محیط اطراف از یکدیگر جدا شده‌اند.

انرژی مکانیکی چیست؟

به مجموع انرژی جنبشی و پتانسیل یک سیستم، انرژی مکانیکی گفته می‌شود. بنابراین انرژی مکانیکی را می‌توان به صورت زیر بیان کرد:

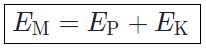
البته به شکلی کلی‌تر می‌توان گفت که حاصل جمع انرژیِ نیرو‌های پایستار برابر با انرژی مکانیکی در نظر گرفته می‌شود. از معروف‌ترین نیرو‌های پایستار، نیرو‌ی گرانش و کشش فنر هستند. نیرو‌های اصطکاکی نیز جزء نیرو‌های غیرپایا در نظر گرفته می‌شوند. توجه داشته باشید که به نیرویی، پایا گفته می‌شود که انرژی منتقل شده در نتیجه نیروی مذکور، وابسته به مسیر نباشد.

کاربرد پایستگی انرژی

زمانی که انرژی یک سیستم پایسته باشد، می‌توان مجموع انرژی آن را در قالب تعدادی پارامتر نوشته و انرژیِ کل را بر حسب دامنه‌های مختلف بیان کرد. در این صورت با برابر فرض شدن انرژی کل در حالت ابتدایی و انتهایی حرکت یک جسم،‌ می‌توان کمیتی خاص را بدست آورد.

مثال ۱

فرض کنید گلف‌ بازی در ماه ضربه‌ای به توپ گلف وارد می‌کند. فرض کنید شتاب گرانشی در ماه برابر با $$1.625 \enspace \frac {m}{s^2}$$ بوده و توپ با زاویه ۴۵ درجه و سرعت اولیه‌ی $$28.28 \enspace \frac { m }{ s }$$ به حرکت در آید. در این صورت بیشترین ارتفاعی که توپ تجربه می‌کند، چقدر خواهد بود؟

فیلم آموزش فیزیک پایه 1 – جامع و کاربردی در فرادرس

کلیک کنید

شاید با توجه به این‌که حرکت توپ در ماه در نظر گرفته شده‌،‌ استفاده از قانون پایستگی بسیار مناسب باشد، چرا که اثرات اصطکاکی نیز وجود ندارد. توپی که در ارتفاع h از سطح ماه قرار گرفته و سرعتش v باشد، انرژیش با استفاده از رابطه زیر بدست می‌آید.

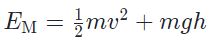
حال رابطه فوق را در دو حالت می‌نویسیم. وضعیت i، ابتدای حرکت توپ در نظر گرفته می‌شود. از طرفی وضعیت f نیز زمانی است که توپ در بیشترین ارتفاعش قرار گرفته است. در حقیقت در ابتدای حرکت، انرژی پتانسیل توپ برابر با صفر بوده و انرژی توپ فقط از نوع جنبشی است. این در حالی است که در بیشترین ارتفاع، توپ تنها سرعت افقی داشته و انرژی در نتیجه حرکت عمودی ندارد. توجه داشته باشید که با توجه به مفاهیم حرکت پرتابی سرعت افقی جسم در طول حرکت ثابت بوده و اندازه آن برابر است با:

$$\large V _ x = V \enspace Cos ( \theta ) = 28.28 \enspace Cos (45) = 20 \enspace m/s$$

بنابراین انرژی جسم در بیشترین ارتفاع فقط ناشی از حرکت در راستای افق است. با نوشتن قانون پایستگی انرژی داریم:

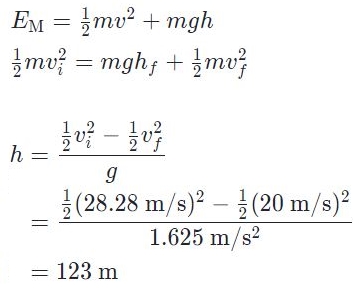
مثال ۲

تصور کنید سنگی از پلی به ارتفاع ۲۰ متر با سرعت اولیه‌ی ۱۵ متر بر ثانیه به سمت پایین پرتاب می‌شود. با صرف نظر کردن از اثرات اصطکاک هوا، سرعت سنگ را در لحظه برخورد به زمین بدست آورید.

با برابر قرار دادن انرژی سنگ در لحظه پرتاب و در لحظه برخورد آن به زمین داریم:

$$\large K _ i + U _ i = K _ f + U _ f$$

بدیهی است که در لحظه برخورد سنگ به زمین، انرژی پتانسیل سنگ برابر با صفر است. نهایتا رابطه فوق به صورت زیر بازنویسی می‌شود:

$$\large \frac { 1 } { 2 } m v_i^2 + mgh {_ i} = \frac { 1 } { 2 } m v_f^2 + mgh {_ f}$$
$$\rightarrow \enspace v _ f = \sqrt { 2 g h + v _ i ^2 }$$

با جایگذاری مقادیر در رابطه فوق، اندازه سرعت در لحظه برخورد برابر می‌شود با:

$$\rightarrow \enspace v _ f = \sqrt { 2( 9.8) (20) + (15) ^2 }=24.8 \enspace m/s$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس دبیرستان
• مجموعه آموزش‌های ریاضی و فیزیک
• تُندی و سرعت — به زبان ساده
• قضیه کار و انرژی -- به زبان ساده
• انبساط گرمایی — به زبان ساده