نظریه اندازه در ریاضیات – مفاهیم و کاربردها
در ریاضیات، «اندازه» (Measure) روی یک «مجموعه» (Set)، یک روش برای نسبت دادن یک عدد به هر یک از زیرمجموعههای آن است. این عدد میتواند به عنوان «اندازه» (Size) چنین مجموعههایی به کار رود. به این ترتیب، اندازه، میتواند درست به مانند طول، سطح و حجم در نظر گرفته شود. همین امر باعث میشود که نظریه اندازه در ریاضیات به شکل کاربردی در همه شاخههای دیگر علوم نیز به کار گرفته شود.


در این نوشتار با توجه به اهمیت نظریه اندازه در ریاضیات، به معرفی اصطلاحات مطرح شده در این نظریه میپردازیم و با برخی از اندازههای معروف در نظریه اندازه در ریاضیات آشنا خواهیم شد.
نظریه اندازه در ریاضیات
همانطور که اشاره شد، در نظریه اندازه به هر زیرمجموعه از یک فضا، مقداری عدد نسبت داده میشود. از اندازههای معروف در نظریه مجموعهها، میتوان به «اندازه لبگ» (Lebesgue Measure) در «فضای اقلیدسی» (Euclidean Space) اشاره کرد.
در اندازه لبگ، طول (یا فاصله اقلیدسی) در مجموعه اعداد حقیقی، به صورت طول فاصله در نظر گرفته میشود. بنابراین اگر زیر مجموعه از اعداد حقیقی به شکل یک بازه در نظر گرفته شود، اندازه لبگ برای این زیرمجموعه به صورت در خواهد آمد.
با توجه به این موضوع میتوان اندازهها روی مجموعه را به صورت یک تابع در نظر گرفت که دامنه آن زیرمجموعههای بوده و برد یا مجموعه مقادیر آن را اعداد نامنفی محسوب کرد.
از خصوصیات جالبی که باید برای چنین تابعی فرض کرد، خاصیت جمعی (Additive) بودن آن است. با توجه به این موضوع میتوانیم مجموعهها را با توجه به اندازه مورد نظر، به ترتیب از کوچک به بزرگ بچینیم. این موضوع درست به مانند اعداد اصلی در مجموعه اعداد است که بزرگی هر مجموعه را با توجه به اعداد آن در نظر میگرفت. با اضافه کردن اعضای جدید، اندازه مجموعه نیز بزرگتر میشود. چنین مفهومی اندازههای شمارشی (Counting Measure) را پدید میآورد.
موضوع وجود خاصیت جمعی و اندازه شمارشی در ادامه مطلب مورد بحث قرار خواهد گرفت.
نظریه اندازه در میانه قرن ۱۹ و ۲۰ توسط ریاضیدانهایی مانند «امیل بورل» (Emile Borel)، «هنری لبگ» (Henri Lebesgue)، «جان رادون» (John Radon) و «مارسی فرچه» (Maurcie Frechet) صورت گرفت.
از مهمترین کاربردهای نظریه اندازه (Measure Theory) به «انتگرال لبگ» (Lebesgue Integral) و تبیین اصول ریاضی برای تابع احتمال که به اصول احتمال کولموگروف (Kolmogrove Axioms of {probability) معروف است، میتوان اشاره کرد.
انتگرال گیری میتواند به عنوان یک اندازه روی فضا حالت تعمیم یافته انتگرال در فضای اقلیدسی باشد. در نتیجه توسعه انتگرال لبگ روی فضای اقلیدسی میتواند اندازههای دیگری روی فضاهای غیراقلیدسی نیز پدید آورد. برای مثال «انتگرال ریمان» (Reimann Integral) یا تابع احتمال میتواند اندازههایی باشند که در چنین فضاهایی مورد نظر هستند.
نکته: تفاوت اصلی بین انتگرال ریمان و تابع احتمال آن است که مجموعه (یا انتگرال) روی مجموعه برای تابع احتمال برابر با ۱ خواهد بود. بنابراین تابع احتمال حالت نرمال یا استاندارد شده به صورت یک اندازه است که توسط انتگرال ریمان تعیین شده است.
تعریف اندازه در ریاضیات
قبل از آنکه به تعریف اندازه در ریاضیات بپردازیم، با یک اصطلاح مهم آشنا میشویم. «سیگما-میدان» (Sigma Field) یا «سیگما جبر» (-algebra)، به میدان خاصی از یک مجموعه اشاره میکند.
گردایه که براساس زیر مجموعههای یک مجموعه مانند ایجاد شود و در همه شرطهای زیر صدق کند، «سیگما-میدان» () یا «سیگما-جبر» () گفته میشود.
- مجموعه تهی () و باید در F باشند. به این معنی که
- اگر در باشد باید مکمل نیز در وجود داشته باشد. $$ E \in F \rightarrpw E' \in F $$
- اگر در باشند، دنبالهای از مجموعهها دو به دو جدا از هم باشند، آنگاه اجتماع این مجموعهها، نیز در است.
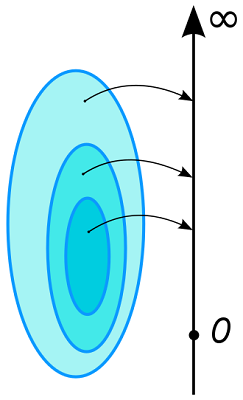
فرض کنید یک مجموعه و نیز یک سیگما-میدان باشد. تابع از به مجموعه اعداد حقیقی توسعه یافته، یک اندازه است، اگر در شرایط زیر صادق باشد.
- نامنفی بودن (Non-Negativity): برای همه مجموعههای بر این اساس خواهد بود.
- اندازه مجموعه تهی (Null Empty Set): برای مجموعه تهی، مقدار اندازه صفر است. یعنی .
- جمعپذیری شمارشپذیر (Countable Additivity): برای همه گردایههای شمارشپذیر به طور دو به دو مجزا هستند روی هستند رابطه زیر برقرار است.
چنین وضعیتی باید به شکلی باشد که حداقل یکی از ها دارای اندازه متناهی باشد. در این صورت به طور خودکار مجموعه تهی اندازه صفر خواهد داشت، زیرا طبق اصل جمعبذیری شمارشپذیر، داریم:
طرف راست این تساوی فقط زمانی همگرا است که .
اگر از اصول گفته شده، فقط دو اصل دوم و سوم، برقرار باشند و حداکثر یا حداقل مقدار برابر با یا باشد، آنگاه را اندازه علامتدار (Signed Measure) مینامند.

فضای اندازهپذیر
دوتایی را یک فضای اندازهپذیر (Measurable Space) مینامند. به این ترتیب هر عنصر یا اعضای یک مجموعه اندازهپذیر (measurable Set) خواهد بود.
به این ترتیب اگر و دو فضای اندازهپذیر باشند، آنگاه تابعی از به ، اندازهپذیر است اگر برای هر مجموعه -اندازهپذیر مثال ، تصویر معکوس آن یک مجموعه -اندازهپذیر باشد.
همچنین میتوان نشان داد که ترکیب دو اندازه، میتواند یک اندازه جدید پدید آورد.
سه تایی یک «فضای اندازه» (Measure Space) نامیده میشود. اندازه احتمال (Probability Measure) هم یک اندازه است که مقدار کل اندازه برایش برابر با ۱ است. در نتیجه داریم:
به همین ترتیب فضای احتمال، شامل یک فضای اندازه و تابع یا اندازه احتمال خواهد بود.
مثالهایی از اندازههای معروف
در این قسمت به بعضی از فضاهای اندازه اشاره خواهیم کرد که کاربردهایی در «نظریه احتمال» (Probability Theory) و دیگر قسمتهای ریاضیات دارند.
- اندازه شمارشی (Counting Measure)، اندازهای است که روی مجموعههای شمارشپذیر تعریف شده و به هر مجموعه، تعداد اعضای آن را نسبت میدهد. به این ترتیب برابر با تعداد اعضای مجموعه است.
- اندازه لبگ (Lebesgue Measure) که روی مجموعه اعداد حقیقی تعریف شده که به صورت فاصلههای باز یا بسته تعریف میشوند. برای مثال اندازه لبگ برای بازه برابر است با ۱. .
- اندازه هاسدورف (Hausdorff Measure)، که مانند اندازه لبگ بوده ولی روی مجموعههایی با ابعاد غیر صحیح مانند فراکتالها (Fractal Sets) اعمال میشود.
- اندازه احتمال (Probability Measure) که فقط مقادیر در بازه صفر تا یک را اختیار میکند و برای مجموعه مقداری برابر با یک دارد. چنین اندازهای در اصول احتمال صدق میکند.
- اندازه دیراک ( Dirac Measure) که با نماد نشان داده میشود نیز یک اندازه است بطوری که بطوری که همان تابع نشانگر است. در این حالت مقدار این اندازه برای یک مجموعه برابر با ۱ خواهد بود اگر این مجموعه شامل نقطه باشد، در غیر این صورت مقدار اندازه برای چنین مجموعهای برابر با صفر است.
خصوصیات اندازه
فرض کنید که یک اندازه است. در این صورت خواص زیر، برای آن در نظر گرفته میشود.
یکنوای اندازه
همانطور که قبلا نیز اشاره شد، به وسیله اندازهها، میتوانیم مجموعهها را دارای ترتیب کنیم. این ویژگی اندازهها به یکنوایی (Monotonicity) معروف است.
دو مجموعه - اندازهپذیر و را در نظر بگیرید، بطوری که . در این صورت خواهیم داشت .
زیر جمعپذیری شمارشپذیر
برای هر دنباله شمارشپذیر از زیرمجموعههای که -اندازهپذیر باشند، خاصیت زیرجمعپذیری (Subaddivity) وجود دارد. به این معنی که برای چنین دنبالهای خواهیم داشت:
به این موضوع توجه داشته باشید که در این رابطه، احتیاجی به جدا از هم بودن هر یک از مجموعههای نیست و در این رابطه ضرورتی وجود ندارد.
پیوستگی از پایین
در اینجا هم دنبالهای شمارشپذیر از زیرمجموعههای -اندازهپذیر را در نظر داشته باشید. این دنباله یک دنباله صعودی است به این معنی که برای هر داریم . با توجه به این اطلاعات رابطه زیر نیز برای اندازه اجتماع نامتناهی ولی شمارشپذیر آنها برقرار است. این خاصیت در نظریه اندازه «پیوستگی از پایین» (Continuity from below) نامیده میشود.
پیوستگی از بالا
این بار یک دنباله نزولی از زیرمجموعههای را در نظر بگیرید که در آن برای هر رابطه برقرار است. با این فرض، اشتراک چنین دنبالهای نیز -اندازهپذیر خواهد بود. به علاوه در صورتی که حداقل یکی از ها دارای اندازه متناهی باشد رابطه زیر برقرار است. به این ترتیب اندازه اشتراک چنین دنبالهای برابر است با حد اندازه زمانی که به سمت بینهایت برود.
چنین خاصیتی در نظریه اندازه به پیوستگی از پایین (Continuity from above) اندازه مشهور است.
نکته: باید توجه داشت که در نظریه اندازه این خاصیت برای زمانی که حداقل یکی از ها اندازه متناهی نداشته باشد، برقرار نیست. برای مثال، فرض کنید که به ازاء هر مجموعه به صورت تعریف شده باشد. در این صورت همه اعضای این دنباله دارای اندازه لبگ نامتناهی هستند ولی اشتراک آنها، تهی است که اندازهای برابر با صفر دارد.
اندازههای سیگما-متناهی
فضای اندازه را متناهی گویند اگر یک عدد حقیقی متناهی (مقداری به جز ) باشد. اندازههای متناهی غیر صفر را میتوان مترادف با «اندازه احتمال» (Probability Measure) در نظر گفت زیرا برای چنین اندازهای میتوان مقدار احتمال را برای یک پیشامد مثل به صورت فرض کرد.
اندازه را سیگما-متناهی گویند اگر بتوان را به صورت اجتماع شمارشپذیری از مجموعههای اندازهپذیر در آورد که هر یک دارای اندازهای متناهی باشند. به بیان دیگر یک مجموعه از فضای اندازه را با اندازه سیگما-متناهی گوییم اگر بتوان آن را به صورتی نوشت که به شکل اجتماعی شمارشپذیر از مجموعههایی با اندازه متناهی درآید.
برای مثال مجموعه اعداد حقیقی و اندازه لبگ را در نظر بگیرید. با تعریف ارائه شده، اندازه لبگ یک اندازه سیگما متناهی خواهد بود. مثلا فاصلههای بسته را با فرض کنید. چنین مجموعه یا فاصلههایی، شمارشپذیر بوده و هر یک دارای اندازه لبگ برابر با ۱ هستند ولی میتوان مجموعه اعداد حقیقی را براساس اجتماع شمارشپذیر از چنین مجموعههایی ایجاد کرد.
در عوض اندازه شمارشی (Counting Measure) یک اندازه سیگما-متناهی روی اعداد حقیقی در نظریه اندازه نیست. زیرا نمیتوان براساس اجتماع شمارشپذیری از مجموعههای با اندازه متناهی، مجموعه اعداد حقیقی را ساخت.
مجموعه با اندازه صفر و اندازه کامل
یک مجموعه اندازهپذیر را یک مجموعه صفر (Null Set) مینامیم اگر اندازه آن برابر با صفر باشد. در این صورت اگر یک مجموعه -اندازهپذیر باشد، انگاه یک مجموعه صفر است اگر . زیرمجموعه یک مجموعه صفر را یک مجموعه خرد یا ناچیز (negligible) مینامند.
هر چند ممکن است زیرمجموعههای خرد یک مجموعه اندازهپذیر، خود دارای اندازه نباشند ولی در صورت اندازهپذیر بودن چنین زیرمجموعههای، به طور خودکار اندازه آنها صفر خواهد بود.
اگر همه زیرمجموعههای ناچیز یک فضای اندازه، اندازهپذیر باشند (واضح است که اندازه آنها نیز صفر هستند) آن اندازه را کامل (Complete) میگویند. به این ترتیب اندازه لبگ در مجموعه اعداد حقیقی، یک اندازه کامل خواهد بود.
خلاصه و جمعبندی
در این نوشتار با نظریه اندازه در ریاضیات آشنا شدیم. همچنین خصوصیات و اصطلاحاتی که برای مجموعههای اندازهپذیر وجود دارد نیز مورد بحث قرار گرفت. با توجه به نزدیکی نظریه احتمال و نظریه اندازه، این حوزه از ریاضیات بخصوص برای کسانی که با آمار و احتمالات سروکار دارند، جالب بوده و مبانی نظریه احتمال را برایشان بوسیله نظریه اندازه در ریاضیات روشنتر میکند.
اگر مطلب بالا برایتان مفید بوده است، آموزشها و نوشتارهای دیگر مجله فرادرس که ادامه قابل مشاهده هستند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- آموزش مبانی آنالیز حقیقی
- مجموعه آموزشهای آمار و احتمالات
- فضای متریک و نامساوی مثلثی — به زبان ساده
- آزمایش تصادفی، پیشامد و تابع احتمال
- قضیه مقدار میانی (Intermediate Value Theorem) — به زبان ساده
^^













متاسفانه اساتید در زمان توضیح مجموعه های اندازه پذیر بدون مقدمه و بدون انگیزه تعریف شروع میکنن تعریف موضوع و سپس بعد چن جلسه تاریخ ازمون اعلام میکنن. به نظر من این متد خیلی دیگه اثری نداره و باعث میشه دانشجو دنبال تحقیق نره و موضوع براش گیج کننده باشه و احساس میکنه حتما به اجبار هم شده مطااب فقط حفظ کنه نه مفهومی یاد بگیره.