مکان هندسی — به زبان ساده

شاید تابحال با خود فکر کرده باشید که چگونه می‌توان مفاهیمی هندسی همچون بیضی، دایره، هذلولی یا حتی خط را تعریف کرد. معمولا این اشکال از نقاطی تشکیل شده‌اند که دارای ویژگی یا ویژگی‌هایی مشابه‌اند. به این نقاط با ویژگی مشابه، مکان هندسی گفته می‌شود. در این مطلب قصد داریم تا مکان هندسی را توضیح داده و مثال‌هایی نیز از آن ارائه دهیم.

مکان هندسی چیست؟

مکان هندسی، به مجموعه نقاطی از فضا گفته می‌شود که دارای یک یا چند ویژگی مشترک باشند. تا آغاز قرن بیستم، یک شکل هندسی به عنوان مجموعه نقاطی از یک صفحه شناخته نمی‌شد. بلکه هریک از اشکال به عنوان مفهومی مجزا تلقی می‌شدند که ممکن بود نقاطِ صفحه روی آن قرار بگیرند. برای نمونه، دایره را می‌توان به عنوان منحنی در نظر گرفت که فاصله نقاط آن از یک نقطه ثابت که همان مرکز است، برابر با عدد ثابتی باشد.

فیلم آموزش هندسه پایه دهم – هندسه 1 در فرادرس

کلیک کنید

در ریاضیات مدرن، مفاهیم مشابهی در مورد اشکال پیچیده‌تر هندسی نیز به کار می‌رود. برخلاف تعریف مبتنی بر مکان هندسی، روش کلاسیک، از بیان مجموعه‌ای از بینهایت نقطه جلوگیری می‌کرد. این جلوگیری منجر به دست نیافتن به خودِ مفهوم بینهایت توسط ریاضیدانان کلاسیک نیز می‌شد.

مثال‌هایی در صفحه تخت

بسیاری از مفاهیم هندسی در فضای دوبعدی را می‌توان با استفاده از مکان هندسی نقاط تعریف کرد. در ادامه چند مورد از مهم‌ترین این تعاریف ارائه شده‌اند.

۱. مجموعه نقاطی از صفحه که فاصله آن‌ها از دو نقطه ثابت، مقداری برابر باشد، نشان‌دهنده خطی عمود بر خط متصل‌کننده دو نقطه است. برای بدست آوردن این مکان هندسی کافی است دو دایره به مراکز هریک از این نقاط رسم کرده و آن‌ها را با هم قطع دهید. در این صورت با اتصالِ خطِ اتصال نقاط مشترک، مکان هندسی بیان‌شده بدست خواهد آمد. در انیمیشنی که در ادامه آمده، نحوه ترسیم این خط ارائه شده است.

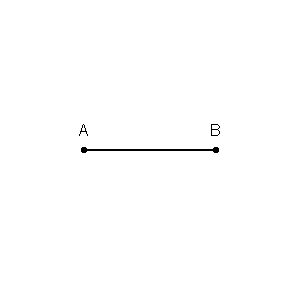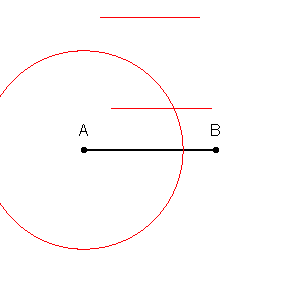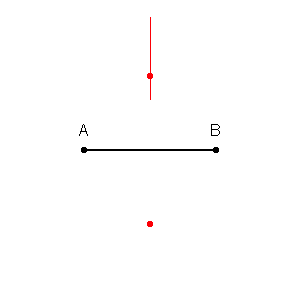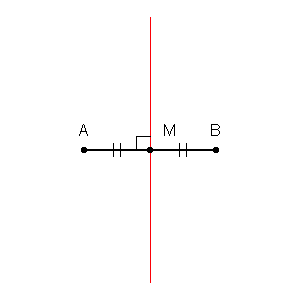
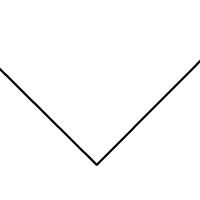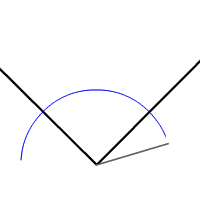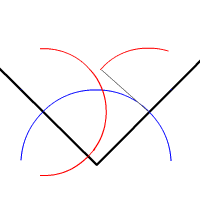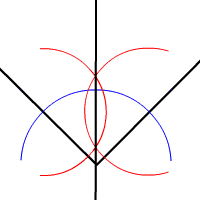
۲. مجموعه نقاطی از صفحه که فاصله آن‌ها از دو خط مقداری برابر باشند، یک نیمساز را تشکیل می‌دهند. برای بدست آوردن این نیم‌ساز نیز کافی است تا در ابتدا دایره‌ای به مرکز تقاطع دو خط ترسیم کرده و دوباره دو دایره به مراکز تقاطع دایره‌ اول با خطوط رسم کنید. در مرحله آخر نیز با ترسیم خط میان محل تقاطع دو دایره، مکان هندسی نقاط یا همان نیمساز بدست می‌آید. در انیمیشن زیر نحوه ترسیم نیم‌ساز نشان داده شده است.

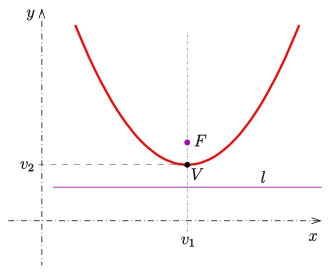
۳. سهمی، به مجموعه نقاطی از صفحه گفته می‌شود که فاصله آن از یک خط و یک نقطه برابر باشد. در شکل زیر مسیر یک سهمی نشان داده شده است.

۴. به مجموعه نقاطی از صفحه که فاصله آن‌ها از یک نقطه ثابت، برابر باشند، دایره گفته می‌شود. البته پیش‌تر، در مطلبی مجزا در مورد نحوه بدست آوردن معادله دایره نیز صحبت کردیم که مطالعه آن برایتان خالی از لطف نخواهد بود.

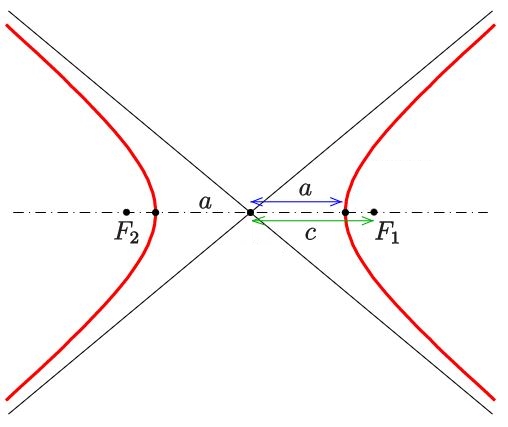
۵. هذلولی به مجموعه نقاطی از صفحه اطلاق می‌شود که اختلاف فاصله آن‌ها از دو نقطه، برابر با مقداری ثابت باشد. دو نقطه مذکور را کانون هذلولی می‌نامند. در شکل زیر یک هذلولی به همراه کانون‌هایش نشان داده شده است.

۶. بیضی به مجموعه نقاطی اشاره می‌کند که مجموعِ فاصله آن‌ها از دو نقطه ثابت، عددِ ثابتی باشد. در حقیقت دایره، بیضی‌ای است که این حاصل جمعِ فاصله نقاط روی آن از دو نقطه قرار گرفته روی هم (مرکز دایره)، برابر با قطر است. در شکل زیر سه بیضی و کانون‌های آن‌ها نشان داده شده‌اند.

در دیگر شاخه‌های ریاضی (و حتی دیگر علوم) نیز مکان‌های هندسی قابل تعریف هستند. برای نمونه مجموعه مندلبرو، مفهومی است که با استفاده از مکان هندسی در دینامیک مختلط تعریف می‌شود.

توجه داشته باشید که تعریف ارائه شده برای هر شکل هندسی را می‌توان با نوشتن شکل ریاضیاتی مکان هندسی تعریف کرد. در این رابطه در ادامه دو مثال ذکر شده است.

مثال ۱

مکان هندسی نقاط $$P$$ را بیابید. فرض کنید نسبت فاصله این نقطه، نسبت به دو نقطه $$A = ( - 1 , 0 )  ,  B = ( 0 , 2 )$$ برابر با $$k = d _ 1 / d _ 2 = 3$$ است.

فیلم آموزش ریاضی و آمار 1 – پایه دهم علوم انسانی در فرادرس

کلیک کنید

با استفاده از تعریف داریم:

$$\large | P A | = 3 | P B |$$

بدیهی است که فاصله نقطه‌ $$P = ( x , y )$$ با نقطه‌ای هم‌چون $$( x _ 0 , y _ 0 )$$ برابر است با:

$$\large l = \sqrt { \left( ( x - x _ 0 ) ^ 2 + ( y - y _ 0 ) ^ 2 \right )}$$

بنابراین کافی است رابطه فوق را برای دو نقطه $$A$$ و $$B$$ بیان کرده و با برابر قرار دادن آن‌ها، نهایتا معادله نقاط $$P$$ بدست خواهند آمد. نهایتا معادله نقاط $$P$$ برابر می‌شوند با:

$$| P A | = 3 | P B |$$ $${ \displaystyle \Rightarrow | P A | ^ { 2 } = 9 | P B | ^ {2 } }$$ $${ \displaystyle \Rightarrow 8 ( x ^ { 2} + y ^ { 2 } ) - 2 x -36 y + 3 5 = 0 }$$ $${\displaystyle \Rightarrow \left ( x - { \frac { 1 } { 8 } } \right ) ^ { 2 } + \left ( y - { \frac { 9 } { 4 } } \right ) ^ { 2 } = { \frac { 4 5 } { 6 4 } } }$$

بدیهی است رابطه فوق، نشان‌دهنده دایره‌ای به شعاع $$\frac { 4 5 } { 6 4 }$$، با مرکزِ $$( \frac { 1 } { 8 } , \frac { 9 } { 4 } )$$ است. در شکل زیر نقاطِ $$P , B , A$$ و هم‌چنین مکان هندسی مذکور نشان داده شده‌اند.

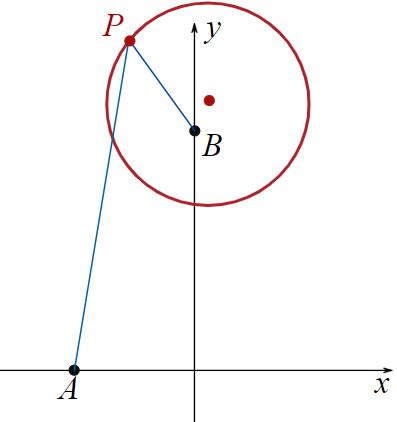
مثال ۲

خطِ $$A B$$ را به طول $$c$$ در نظر بگیرید. مکان هندسی نقاط $$C$$ را به شکلی بیابید که میانه ترسیم شده از $$A$$ و $$C$$، به یکدیگر عمود باشند.

فیلم آموزش هندسه ۲ – پایه یازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

به منظور بدست آوردن معادله مکان هندسی، در ابتدا باید تصویری از سوال بیان شده را در ذهن داشته باشید. در شکل زیر مثلث ناشی از یکی از نقاط فرضیِ $$C$$ نشان داده شده است.

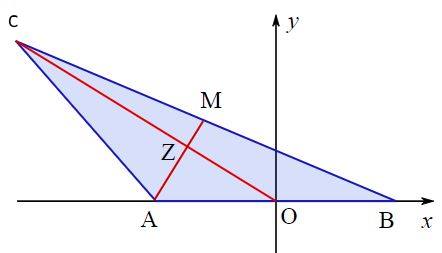
با توجه به این‌ که خط $$A B$$ ثابت فرض شده، محور $$x y$$ به نحوی در نظر گرفته شده که مختصات $$A$$ و $$C$$ به صورت زیر باشند.

$$A ( − \frac { C } { 2 } , 0 ) \ \ , \ \ B ( \frac { C } { 2 } , 0 )$$

با فرض این‌که مختصاتِ $$C = ( x , y )$$ باشد، در این صورت مختصات مرکزِ $$B C$$ برابر است با:

$$\large M ( ( 2 x + c ) / 4 ,   y / 2 )$$

از طرفی دیگر شیب میانه ترسیم شده از $$C$$ نیز برابر با $$\frac { y } { x }$$ است. هم‌چنین شیب خط $$A M$$ برابر است با:

$$\large M ( \frac { 2 x + c } { 4} , \frac { y } { 2 } )$$

با توجه به عمود بودن دو خط، باید حاصل‌ضرب شیب آن‌ها را برابر با $$- 1$$ قرار داد. بنابراین معادله مکان هندسی مذکور به شکل زیر بدست می‌آید.

$${ \displaystyle \large { \frac { y } { x} } \cdot { \frac { 2 y } { 2 x + 3 c } } = - 1 }$$ $${ \displaystyle \large 2 y ^ { 2 } + 2 x ^ { 2 } + 3 c x = 0 }$$ $${ \displaystyle \large x ^ { 2 } + y ^ { 2 } + ( \frac { 3 c } { 2 } ) x = 0 }$$ $${ \displaystyle \large ( x + \frac { 3 c } { 4 } ) ^ { 2 } + y ^{ 2 } =\frac { 9 c ^ { 2 } } { 16 } }$$

رابطه فوق نیز نشان‌دهنده معادله یک دایره است. در شکل زیر این دایره نشان داده شده است.

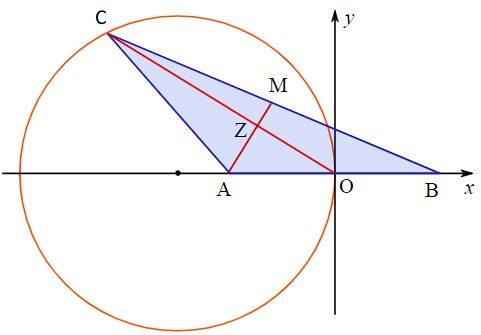
در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی و هندسه، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند: