معادله دیفرانسیل تصادفی – به زبان ساده
«معادله دیفرانسیل تصادفی» (Stochastic Differential Equation) که به اختصار (SDE) نامیده میشود، یک معادله دیفرانسیل است که یک یا چند جمله آن فرآیند تصادفی هستند. این امر باعث میشود که پاسخهای معادله دیفرانسیل تبدیل به یک فرآیند تصادفی شوند. در نتیجه هرچند روشهای حل مشابه معادله دیفرانسیل معمولی است و تفاوتهایی نیز وجود دارد. در این نوشتار به مبانی معادلات دیفرانسیل تصادفی پرداختهایم و قضیه و شرایط مربوط به وجود پاسخ و یکتا بودن چنین معادلاتی را بررسی کردهایم.
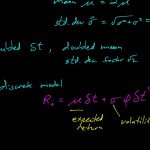
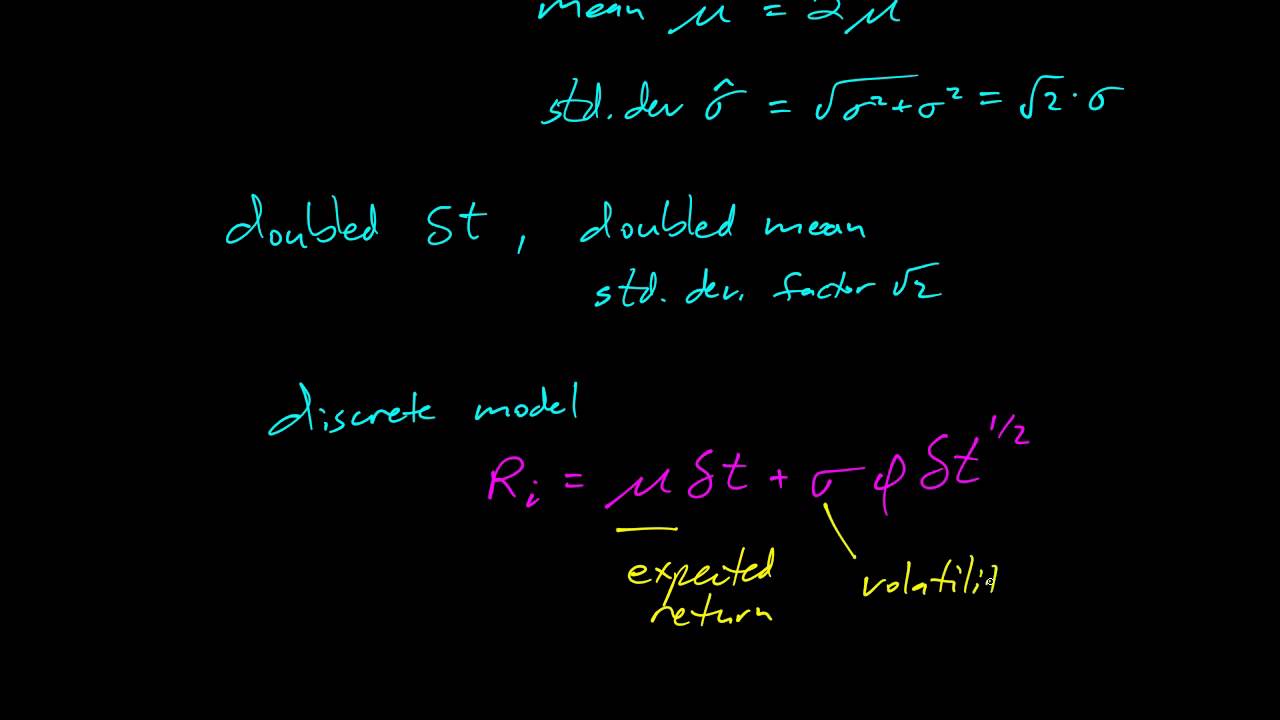
برای آشنایی بیشتر با مفاهیم مربوط به فرآیندهای تصادفی و متغیرهای تصادفی بهتر است مطالب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و فرایند تصادفی (Random Process) — مفاهیم اولیه را مطالعه کنید. همچنین خواندن نوشتارهای معادلات دیفرانسیل — به زبان ساده و معادلات دیفرانسیل مرتبه اول — روشهای حل به زبان ساده نیز خالی از لطف نیست.
معادلات دیفرانسیل تصادفی
معادلات دیفرانسیل تصادفی برای مدلسازی بسیاری از پدیدهها مانند نوسانات قیمت سهام، تغییرات سیستمهای فیزیک در اثر دما و ... به کار میروند.
به طور کل میتوان SDE را یک معادله در نظر گرفت که به همراه یک متغیر تصادفی (مثل نوفه سفید) ارائه شده است. به این ترتیب معادلات دیفرانسیل تصادفی در توصیف حرکت براونی (Brownian Motion) یا فرآیند وینر (Weiner Process) کاربرد خواهد داشت. بعلاوه، فرآیندهای پرش (Jump Processes) نیز میتواند توسط معادلات دیفرانسیل بیان شوند.
پیشزمینه معادلات دیفرانسیل تصادفی
یکی از اولین فعالیتها در بازنویسی معادلات دیفرانسیل به شکل تصادفی، به معادلات حرکت براونی در مقاله مشهور «آلبرت اینشتین» (Albert Einstein) فیزیکدان و ریاضیدان آلمانی بر میگردد.
در همان زمان نیز «ماریان سمولوچوسکی» (Marian Smoluchowski) نیز به بررسی معادلات دیفرانسیل تصادفی برای توصیف و تشکیل مبانی فیزیک آماری پرداخت.
البته شاید بتوان اولین جرقههای ظهور معادلات دیفرانسیل تصادفی را به «لوئیس بچلر» (Loius Bacheller) نسبت داد که در پایاننامه خود به نام «نظریه خیال» به معادلات دیفرانسیل تصادفی یا همان SDE اشاره کرد.
براساس کارهایی که او انجام داد، «پاول لنگوین» (Paul Langavin) مبانی ریاضیاتی وسیعتری برای معادلات دیفرانسیل تصادفی ارائه کرد. این کارها در ادامه توسط «ایتو» (ito) و «استراتونویچ» (Stratonovich) پیگری شد و شاخه جدیدی از ریاضیات به نام معادلات دیفرانسیل تصادفی، پدید آمد.

اصطلاحات و مفاهیم اولیه معادلات دیفرانسیل تصادفی
یکی از معمولترین معادلات دیفرانسیل تصادفی (SDE)، معادله دیفرانسیل معمولی است که در یک طرف تساوی در این معادله، رابطهای برحسب یک نوفه سفید (متغیر تصادفی با توزیع نرمال با میانگین صفر و واریانس ۱) قرار گرفته است.
در اکثر اوقات SDEها براساس یک معادله تفاضلی تصادفی برحسب زمان پیوسته و کراندار در نظر گرفته میشود. البته این نوع معرفی معادلات دیفرانسیل، شاید مناسب نباشد و باید به شکلی واضحتر آن را توصیف و ارائه داد.
معروفترین و البته مناسبترین تفسیر معادلات دیفرانسیل تصادفی توسط «ایتو» (ito) و «استراتونویچ» (Stratonovich) ارائه شده است، که از آن برای بیان ریاضیات مالی استفاده میشود. شیوه دیگر توسط استراتونویچ ارائه شده است که به موضوع تغییر شکل و «ناریختی» (diffeomorphisms) در ریاضیات میپردازد. از ویژگیهای این روش میتوان به پیوسته و محدود بودن زمان در معادلات دیفرانسیل تفاضلی مربوط به روشهای سمولوچوسکی یا معادله Fokker-Planck در فیزیک اشاره کرد. چنین معادلاتی توصیفگر رابطه تغییرات سیستمهای فیزیکی با زمان و ارتباط آن با عوامل تصادفی است که رابطه فیزیکی «فوکر-پلانک» (Fokker-Planck) را تعمیم میدهد.
حساب دیفرانسیل تصادفی
بی شبک، ریاضیاتی که برای توصیف فرآیند وینر و حرکت براونی لازم است بسیار پیچیده و مشکل است. «فرآیند وینر» (Weiner Process) «تقریبا مطمئن» (Almost Surely) در هیچ نقطهای مشتقپذیر نیست. به همین دلیل برای توصیف آن احتیاج به ریاضیات خاصی است که توسط معادلات دیفرانسیل تصادفی، صورت میگیرد.
حساب دیفرانسیل تصادفی به دو بخش یا دو رویکرد، تفکیک میشود. روش اول براساس دیدگاه «ایتو» (it) ایجاد شده که به آن «حساب دیفرانسیل ایتو» (it Stochastic Calculus) گفته میشود. از طرفی در روش دوم از ایدههای استراتونوویچ الهام گرفته و با نام «حساب دیفرانسیل تصادفی استراتونوویچ» (Stratonovich stochastic calculus) از آن یاد میشود.
هر یک از این نگرشها، دارای مزایا و معایبی هستند که کاربرد آنها را در حوزههای خاصی محدود میکند. البته روشهایی برای تبدیل بیان معادلات دیفرانسیل تصادفی با دیدگاه ito به Stratonovich وجود دارد که کار را برای مقایسه سادهتر میکند.
راه حلهای عددی
حل عددی معادلات دیفرانسیل تصادفی و به ویژه معادلات دیفرانسیل جزئی تصادفی (Partial Stochastic Differential Equation) یا به طور خلاصه PSDE، یک زمینه نسبتا جدید است. تقریباً همه الگوریتمهایی که برای حل معادلات دیفرانسیل عادی استفاده میشوند، برای SDE بسیار ضعیف عمل کرده و میزان همگرایی ضعیفی دارند. به این معنی که به کارگیری این روشها باعث پاسخهای یکسانی نخواهند شد. برای مطالعه بیشتر در این زمینه بهتر است كتاب درسی «كلوئدن و پلاتن» (Kloeden & Platen) مربوط به سال 1995 را که با نام «روشهای عددی برای حل معادلات دیفرانسیل تصادفی» (Numerical Solution of Stochastic Differential Equations) منتشر شده است، مطالعه کنید. تکنیکهای ارائه شده در این موارد اغلب روشهای «اویلر-ماریوما» (Euler-Maruyama Method) یا «مایلشتاین» (Milstien Method) و «رانگ-کوتا» (Runge-Kutta) هستند.
کاربردهای معادلات دیفرانسیل تصادفی در فیزیک
در فیزیک، SDE به طور گستردهای به کار گرفته میشود. از دینامیک ذرهای تا دینامیک سیارهای، فضای معادلات دیفرانسیل تصادفی نقش داشته و به خصوص برای سیستمهای پویا (Dynamic System) به منظور در نظر گرفتن آشفتگی در چنین سیستمهایی مورد استفاده قرار میگیرند.
به این ترتیب، SDE را میتوان تعمیم نظریه سیستمهای پویا در نظر گرفت که در آنها، نوفه یا نویزها (Noise) نیز در مدل محسوب میشوند. این موضوع از این نظر اهمیت دارد که سیستمهای واقعی را نمیتوان به صورت مجزا از محیط پیرامونشان در نظر گرفت. در نتیجه عوامل تصادفی در تغییرات آنها نقش داشته و معادلات دیفرانسیل تصادفی یا SDE به خوبی از عهده برآورد و مشخص کردن اثر عوامل تصادفی روی سیستمهای پویا و تعیین رفتار آنها برمیآید.
روش و تکنیکهای استانداردی برای تبدیل معادلات دیفرانسیل مرتبه بالا به چندین معادله دیفرانسیل مرتبه اول وجود دارد. آنچه که در رابطه زیر میبینید، فرم عمومی از SDEها است.
رابطه ۱: فرم معادله دیفرانسیل تصادفی در فیزیک
که در آن ، موقعیت سیستم در فضای حالت است. از طرفی نیز یک «منیفلد دیفرانسیلپذیر» (Differentiable Manifold) در نظر گرفته شده. همچنین نیز میدان بردار جریان است که قواعد تغییرات را مشخص میکند. هم سیستم جفت شده با نویز سفید در نظر گرفته شده است..
اگر یک فضای خطی و ها نیز ثابت باشند، سیستم وابسته به نویزها در رابطه ۱، جمعی خواهد بود. در غیر اینصورت رابطه ۱ به صورت ضربی نوشته میشود. با در نظر گرفتن ثابت بودن توزیع نویزها، SDE دارای یک پاسخ یکتا نسبت به شرایط اولیه است.
کاربردهای معادلات دیفرانسیل تصادفی در احتمالات و ریاضیات مالی
نمادهای مورد استفاده برای SDE در تئوری احتمال (و در بسیاری از کاربردهای تئوری احتمال، به عنوان مثال ریاضیات مالی) کمی با فیزیک متفاوت است. این نمادگذاری، باعث میشود که ماهیت عملکرد تصادفی زمان نسبت به فرمولهای فیزیکی صریحتر بیان شود. به تعبیر دقیق ریاضی، را نمیتوان به عنوان یک تابع معمولی در نظر گرفت، بلکه باید آن را یک تابع عمومی و تعمیم یافته محسوب کرد.
اجازه دهید برای روشنتر شدن موضوع از زبان ریاضی استفاده کنیم. البته بیان ریاضیاتی از نقطه نظر فیزیکی، شفافتر و واضحتر رابطه دیفرانسیل تصادفی را نشان میدهد.
فرم عمومی برای SDE به شکل زیر در نظر گرفته میشود.
رابطه ۲: معادله دیفرانسیل تصادفی برای فرآیندهای تصادفی
در اینجا بیانگر یک فرآیند وینر (حرکت براونی استاندارد) است. این شکل از معادله دیفرانسیل به کمک رابطه انتگرالی زیر بهتر مشخص میشود.
رابطه ۳: معادله دیفرانسیل تصادفی برحسب انتگرال برای فرآیندهای تصادفی
رابطه ۳، به خوبی حالت عمومی رفتار فرآیند تصادفی وابسته به زمان پیوسته (Continuous Stochastic Process) برای را نشان میدهد. مشخص است که این رابطه برحسب جمع «انتگرال لبگ» (Lebesgue Integral) و «انتگرال ایتو» (ito Integral) نوشته شده است.
به طور شهودی میتوان معادله دیفرانسیل تصادفی را در حوزه احتمال تغییرات در بازه کوتاهی از زمان در نظر گرفت که در آن این تغییرات دارای توزیع نرمال با میانگین و واریانس است. از طرفی آینده این فرآیند به گذشته آن وابسته نیست. این خاصیت به عنوان ویژگی عدم حافظه (Memoryless) شناخته میشود. همانطور که میدانید، در فرآیند یا «زنجیره مارکفی» (Markov Chain)، چنین ویژگی وجود دارد.
این امر به این علت است که میزان افزایش یا تغییرات در فرآیند حرکت براونی استاندارد، مستقل و دارای توزیع نرمال است. تابع نیز به «ضریب نفوذ» (Drift Coefficient) شناخته میشود، در حالیکه را به نام «ضریب پراکنش» (Diffusion Coefficient) میشناسیم. بنابراین فرآیند تصادفی را براساس این دو پارامتر شناخته و میدانیم که در خاصیت و ویژگی مارکفی صدق میکند.
در این حالت، دو تعریف متفاوت از پاسخ معادله SDE ارائه شده است که به آنها «پاسخ قوی» (Strong Solution) و «پاسخ ضعیف» (Weak Solution) گفته میشود. هر دو این پاسخها وابسته به وجود انتگرالهای مربوطه هستند و را فرآیندی میشناسند که جوابهای رابطه 2 را مشخص میکند.
تفاوت این پاسخها به فضای احتمالی () متفاوتی که هر یک از پاسخها از آن حاصل میشوند بر میگردد. پاسخ ضعیف شامل اندازهها و تابع توزیع و فرآیند تصادفی است که در معادله انتگرالی رابطه 3 صدق میکند. در عوض پاسخ قوی برحسب رابطه 2 نوشته شده و به فضای احتمال و تابع توزیع متغیر تصادفی تکیه دارد.
به عنوان یک مثال مهم در این زمینه میتوان به «حرکت براونی هندسی» (Geometric Brownian Motion) اشاره کرد. در این حالت دیفرانسیل به شکل زیر نوشته میشود.
رابطه ۴: معادله دیفرانسیل تصادفی برای حرکت براونی هندسی
رابطه ۴، میتواند به عنوان معادله تغییرات پویا قیمت یک سهم در ریاضیات مالی نظر گرفته شود.
وجود و یکتا بودن پاسخهای معادله دیفرانسیل تصادفی
همانطور که برای معادلات دیفرانسیل عادی و جزئی قطعی (Deterministic) و غیر تصادفی، وجود پاسخ و یکتایی آن مهم است، این امر برای معادلات دیفرانسیل تصادفی نیز اهمیت دارد. به همین علت به دنبال روشها یا قضیههایی هستیم که بواسطه آن وجود پاسخ و همچنین منحصر به فرد بودن آن را مشخص کند.
آنچه که در ادامه خواهد آمد، بخشی از قضیه وجود و یکتایی معادله دیفرانسیل تصادفی در فضای اقلیدسی بُعدی یعنی است که توسط یک حرکت براونی مانند در فضای بُعدی ایجاد شده است. اثبات مربوطه را میتوانید در (+) مشاهده کنید.
قضیه وجود و یکتایی پاسخ معادله دیفرانسیل تصادفی
فرض کنید و داشته باشیم:
که در آنها و «توابع اندازهپذیر» (Measurable Function) هستند. رابطهای که برای این اندازهها میتوان در نظر گرفت برحسب ثابتهای و به شکل زیر است.
رابطه بالا برای هر و هر در فضای اقلیدسی () صادق است به شرطی که در رابطه زیر صدق کند.
فرض کنید یک متغیر تصادفی است که از سیگما میدان تولید شده توسط مستقل است. توجه داشته باشید که در آن در نظر گرفته شده. از طرفی گشتاور دوم (Second moment) متغیر تصادفی نیز موجود و متناهی است.
معادله دیفرانسیل تصادفی / مسئله مقدار اولیه (differential equation/initial value problem) که به شکل زیر نوشته شده باشد، بطور تقریبا مطمئن (Almost Surley) دارای جواب منحصر به فرد برحسب زمان (پیوسته) خواهد بود.
$$ \large \mathrm{d} X_{t} = \mu (X_{t}, t) \, \mathrm{d} t + \sigma (X_{t}, t) \, \mathrm{d} B_{t} \mbox{ for } t \in [0, T];\\ \large {\displaystyle X_{0}=Z;} $$
توجه داشته باشید که دراین حالت تحت فیلتر که براساس و تولید شده، قرار گرفته است. مشخص است که بوده و داریم:
بعضی از معادلات دیفرانسیل تصادفی صریح قابل حل
معادله دیفرانسیل تصادفی خطی زیر شکل کلی برای چنین حالتی را نشان میدهد.
که در آن داریم:
معادله دیفرانسیل تصادفی کاهشی (Reducible SDE):
در ادامه دو حالت برای معادله دیفرانسیل کاهشی را مشاهده خواهید کرد.
حالت اول
که در آن تابع یک تابع دیفرانسیلپذیر بوده و در نتیجه تشکیل یک معادله دیفرانسیل تصادفی برحسب رابطه «استراتونویچ» (Stratonovich) به شکل زیر میدهد.
پاسخهای عمومی این معادله به صورت زیر هستند.
بطوری که در آن به شکل زیر بدست میآید.
رابطه 5: تابع
حالت دوم
معادله دیفرانسیل زیر را در نظر بگیرید.
در این جا باز هم تابع یک تابع دیفرانسیلپذیر بوده و یک معادله دیفرانسیل تصادفی برحسب رابطه «استراتونویچ» (Stratonovich) در نظر گرفته میشود. فرم این معادله را در ادامه مشاهده میکنید.
با اندکی تغییرات رابطه بالا را به شکل زیر میتوان به صورت کاهشی یا مرتبه کمتر، نمایش داد.
واضح است که در رابطه اخیر، بوده و در آن براساس رابطه 5، بدست خواهد آمد. در این حالت، پاسخ معادله دیفرانسیل تصادفی، مطابق با که در زیر معرفی شده، خواهد بود.
خلاصه و جمعبندی
در این نوشتار با مفهوم معادلات دیفرانسیل تصادفی آشنا شده و مبانی آن را فرا گرفتیم. در همین راستا با توجه به تصادفی بودن پاسخها، چنین معادلاتی مرتبط با فرآیندهای تصادفی نیز خواهند بود. در نتیجه تغییرات فرآیند در واحد زمان را توسط این معادلات مدلسازی کرده و حل میکنند. در بسیاری از فرآیندهای مالی که جنبه تصادفی دارد، معادلات دیفرانسیل تصادفی برای حل مشکلات و ایجاد مدلهای احتمالی به کار گرفته میشوند.












