مدار منطقی چیست؟ – مفاهیم پایه به زبان ساده
«مدار منطقی» (Logic Circuit) نوعی مدار الکترونیکی است که بر پایه جبر بولی و منطق دوتایی یا باینری کار میکند، به این صورت که دو بازه مختلف از کمیتی مانند ولتاژ برای تعیین مقادیر بولی درست یا نادرست تعریف میشود. به این ترتیب ورودیهای مدار منطقی به شکل صفر یا یک است. این ورودیها توسط مهمترین اجزای سازنده مدارهای منطقی یعنی «گیتهای منطقی» (Logic Gates) دریافت شده و پس از انجام یک عمل منطقی، خروجی به شکل صفر یا یک ارسال میشود. در این نوشته از مجله فرادرس کاملا توضیح میدهیم که یک مدار منطقی چیست و چگونه کار میکند.
- یاد میگیرید چرا جبر بولی و منطق باینری بنیان مدار منطقی هستند.
- میآموزید گیتهای منطقی چه نقشی در ساخت و عملکرد مدار دارند.
- تفاوت مدارهای ترکیبی و ترتیبی و کاربرد هر یک را یاد میگیرید.
- با انواع گیت منطقی و روش پیادهسازی مدارهای پایه آشنا میشوید.
- با اصول و کاربردهای قضایای دمورگان در سادهسازی مدار آشنا میشوید.
- خواهید توانست مسائل تحلیلی مدار منطقی را به صورت عملی حل کنید.


ابتدا در مورد جبر بولی، سیگنال دیجیتال و تفاوت آن با سیگنال آنالوگ توضیحاتی بهصورت مختصر ارائه میشود. در بخش بعد یاد میگیرید انواع مدار منطقی چیست و مدارهای ترکیبی و مدار حالت چه تفاوتی با هم دارند. همچنین چند نمونه مدار حالت مانند فلیپفلاپ و رجیستر نیز معرفی میشوند. سپس انواع گیتهای منطقی را به همراه جدول صحت یا درستی و نحوه عملکرد آنها کاملا توضیح میدهیم. همچنین برخی قوانین حاکم بر ترکیب گیتهای منطقی مانند «قوانین دمورگان» را بررسی میکنیم. در ادامه چند مثال و تمرین در همین زمینه قرار داده شده است که با بررسی آنها میتوانید کاملا به مبحث گیتهای منطقی مسلط شوید. در آخرین بخشها نیز به توضیح مشخصه گذار یک گیت منطقی و علت کاربرد مقاومتهای پولآپ و پولداون در مدار منطقی خواهیم پرداخت.
مدار منطقی چیست؟
مدار منطقی نوعی مدار الکترونیکی است که در آن یک سری عملیات منطقی روی یک یا چند ورودی دوتایی، دو حالته یا باینری اجرا میشود تا یک خروجی دو حالته تولید شود. عملکرد این مدارها بر پایه جبر بولی است و مهمترین اجزای آنها، دروازهها یا گیتهای منطقی هستند. دو نوع مدار منطقی داریم، مدار ترکیبی و مدار حالت. در مدارهای ترکیبی خروجی فقط به ورودی در همان لحظه وابسته است، اما در مدارهای حالت یا مدارهای منطقی ترتیبی، خروجی به تاریخچه ورودیها وابسته است. در واقع مدار حالت دارای حافظه است.

مدارهای منطقی که بهصورت مدارهای دیجیتالی هم نامگذاری میشوند، جهت انجام محاسبات پیچیده در سیستمهای دیجیتالی مانند کامپیوترها و ماشینحسابها بکار میروند. در کامپیوترها عموما گیتهای منطقی ترکیبی بهصورت زنجیرهای در کنار هم قرار میگیرند، به این شکل که خروجی از یک گیت گرفته شده و بهعنوان ورودی برای گیت دیگر استفاده میشود. چنین فرآیندی یک مدار منطقی میسازد. مدارهای منطقی شامل ترکیبی از چند گیت منطقی باعث شدهاند کامپیوترها در مقایسه با زمانی که فقط از یک گیت ساخته میشدند، حالا قادر به انجام عملیات پیچیدهتری باشند. در بخشهای بعد انواع گیتهای منطقی را با جزئیات کامل معرفی خواهیم کرد.
عملکرد مدارهای منطقی بسیار شبیه به توابع یا روشهای برنامه نویسی است. در یک مدار منطقی سیگنالهای دیجیتال بهعنوان ورودی دریافت میشوند، اطلاعات آنها در فرمت دیجیتالی پردازش میشود و خروجیهای دیجیتالی نیز تولید میشود. برای اینکه مفهوم و روش کار مدارهای منطقی را بهتر درک کنید، توضیحات خود را با مثال ادامه میدهیم و از کوچکترین مدار منطقی شروع میکنیم.
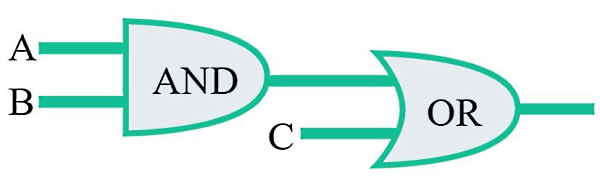
کوچکترین مدار منطقی زنجیرهای است از دو گیت منطقی مانند مداری بهصورت بالا. در این تصویر ابتدا ورودیهای A و B وارد یک گیت منطقی به نام گیت AND میشوند، سپس خروجی این گیت با ورودی C ترکیب شده و وارد گیت دیگری به نام OR شدهاند. در مدارهای منطقی با توجه به اینکه کدام ورودی متناظر با مقادیر عددی صفر یا یک است، نتایج جالبی خواهیم داشت. برای نمونه، فرض کنید در شکل بالا تمام ورودیها یک یا «درست» در نظر گرفته شوند:
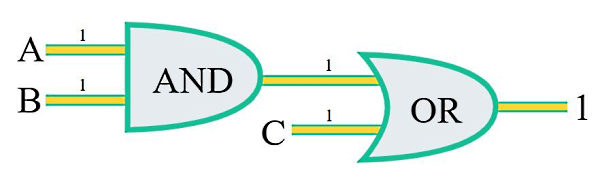
در این صورت خروجی نهایی هم با توجه به نوع عمل منطقی انجام شده روی این ورودیها توسط گیتهای AND و OR برابر با یک است. حالا اگر A و B را روی «نادرست» یا صفر تنظیم کنیم و C را به همان شکل قبل نگه داریم، چه میشود؟
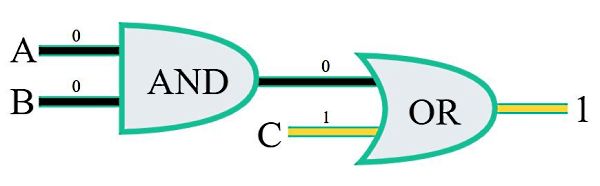
در این شرایط باز هم خروجی نهایی مدار منطقی بالا یک خواهد شد. علت این است که در مرحله آخر گیت OR داریم. گیت OR فقط به یک ورودی «درست» یا یک نیاز دارد تا خروجی یک به ما دهد. در بخشهای بعد توضیح میدهیم که چگونه میتوانیم تشخیص دهیم برای ورودیهای مختلف، خروجی هر نوع گیت منطقی چیست.
جبر بولی چیست؟
گفتیم مدارهای منطقی بر پایه جبر بولی یا منطق دیجیتال کار میکنند. بنابراین در این بخش بهصورت مختصر توضیح میدهیم که جبر بولی و تاثیر آن در یک مدار منطقی چیست. مبنای جبر بولی این است که مقادیر میتوانند دو حالت درست یا نادرست داشته باشند. این دو حالت اغلب با یک و صفر نمایش داده میشود.
برای مثال، وضعیت روشن یا خاموش بودن بلوتوث گوشی در نوار بالای صفحه آن، حاوی اطلاعات باینری است، بلوتوث یا روشن / یک است و یا خاموش / صفر است. اما در همین محیط، کادر نشاندهنده زمان و ساعت در صفحه گوشی نمیتواند چنین اطلاعاتی به ما بدهد. بنابراین مقدار یک داده باینری همواره باید متناظر با یکی از مقادیر صفر یا یک باشد. به این ترتیب یک مدار منطقی باینری هم به مدار منطقیای گفته میشود که روی اعداد دو حالتی یا دوتایی عمل منطقی اجرا میکند. به هر کدام از این اعداد یک بیت گفته میشود. در واقع در مورد مدارهای منطقی باینری از اعداد باینری یا دو حالتی بهعنوان ورودی و خروجی استفاده میشود.
چگونه مدار منطقی را با فرادرس بهتر یاد بگیریم؟
مدار منطقی یکی از دروس مهم دوره کارشناسی در رشتههای مهندسی برق و مهندسی کامپیوتر محسوب میشود. در ادامه این بخش مجموعهای از فیلمهای آموزشی تهیه شده در مجموعه فرادرس را برای شما در نظر گرفتهایم که میتوانید با مشاهده آنها به مباحثی نظیر مدار منطقی و سیستمهای دیجیتال مسلط شوید:
- فیلم آموزش مدار منطقی – مرور و حل مساله فرادرس
- فیلم آموزش مدار منطقی – مرور و تست فرادرس
- فیلم آموزش مدار منطقی – مرور و حل تست کنکور ارشد فرادرس
- فیلم آموزش مدارهای منطقی یا سیستم های دیجیتال فرادرس
- فیلم آموزش فلیپ فلاپ تی T – مدار منطقی ترتیبی سنکرون فرادرس
سیگنال دیجیتال چیست و چه تفاوتی با سیگنال آنالوگ دارد؟
اولین قدم برای اینکه بهتر متوجه شویم یک مدار منطقی چیست و چگونه کار میکند، آشنایی با مفهوم سیگنالهای دیجیتال و آنالوگ است. در حالت کلی اطلاعات موردنظر ما به دو شکل ذخیره میشوند:
- «آنالوگ» (Analogue)
- «دیجیتال» (Digital)
اطلاعات دیجیتالی از یک مجموعه مقادیر یا ارقام مشخص ساخته میشوند، در حالی که اطلاعات آنالوگ از احتمالاتی ساخته میشوند که محدود به یک بازه خاصی هستند. به عبارت دیگر، یک سیگنال دیجیتال فقط میتواند یکی از دو حالت ممکن ON یا OFF را داشته باشد. حالت OFF را منطق صفر یا صفر منطقی و حالت ON را منطق یک یا یک منطقی هم مینامند. این حالتها در مدارهای الکتریکی توسط مقادیر ولتاژ نمایش داده میشوند.
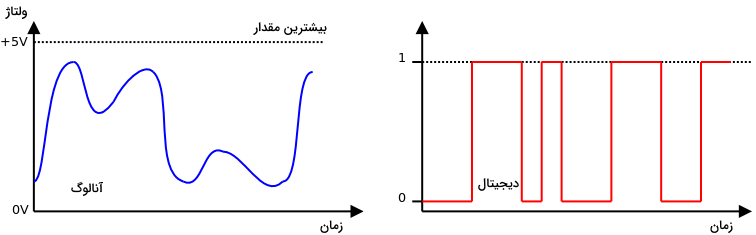
برای مثال نمودارهای بالا را در نظر بگیرید. در این شکل یک منطقی معادل است با ولتاژهایی که معمولا شامل مقادیر مساوی یا بالاتر از میشوند، در حالی که ولتاژ صفر بهعنوان یک منطقی در نظر گرفته میشود. البته این اعداد قانون نیستند و باید ببینیم منبع ولتاژ در مدار چگونه است. برای مثال اگر مدار ما با منبعی به اندازه تغذیه شود، در این صورت منطق یک به هر ولتاژ بالاتر از و منطق صفر به هر ولتاژی زیر مقداری مانند (بسته به اینکه از چه قطعاتی در مدار استفاده شده است) ممکن است تعلق بگیرد. در این مثال مقادیر ولتاژ بین و تعریف نشدهاند، یعنی نه صفر منطقی هستند و نه یک منطقی. پس مقادیری که تعیینکننده صفر و یک منطقی در مدار است، لزوما برای تمام مدارها یکسان نیست.
در مقابل تعریف سیگنال دیجیتال، یک سیگنال آنالوگ میتواند هر مقداری بین دو حد مشخص را بپذیرد. برای مثال اگر مداری توسط یک باتری کار کند، سیگنال آنالوگ میتواند هر مقداری بین صفر تا داشته باشد. یا زمانی که یک مدار با منبع تغذیهای با ولتاژ کار میکند، سیگنال آنالوگ میتواند بین مقادیر و قرار بگیرد. بنابراین مقادیر عددی متناظر با سیگنال آنالوگ میتوانند اعداد منفی هم باشند، برخلاف دیجیتال که فقط اعداد مثبت صفر یا یک است. مدارهای منطقی ممکن است از اجزای مختلفی تشکیل شوند، اما مهمترین جزء یک مدار منطقی، گیتها یا دروازههای منطقی هستند که موضوع بخشهای بعدی است.
انواع مدار منطقی چیست؟
در بخش قبل متوجه شدیم که منظور از دیجیتالی بودن ورودیها و خروجیها در یک مدار منطقی چیست. از آنچه تا اینجا گفتهایم میتوان به این نتیجه رسید که مدارهای منطقی مدارهایی هستند که در آنها خروجی به ورودی وابسته است. همین نکته مبنای تقسیمبندی مدارهای منطقی به دو گروه زیر است:
- مدارهای ترکیبی
- مدارهای ترتیبی یا مدار حالت
در مدارهای ترکیبی، ترکیبی از ورودیها در همان لحظه تعیینکننده این است که خروجی چه خواهد بود، یعنی مدارهای ترکیبی حافظه ندارند. بنابراین اگر ورودی تغییر کند، خروجی نیز «فورا» عوض میشود. اما در مدارهای منطقی ترتیبی اینکه ورودیهای قبلی چه بودهاند نیز مهم است. به عبارت دیگر، مدارهای حالت دارای حافظه هستند و خروجی آنها به ورودیهای لحظات قبل هم بستگی دارد.
بنابراین در مدارهای ترتیبی اگر ورودی تغییر کند، خروجی بلافاصله در همان لحظه تغییر نمیکند. خروجی چنین مداری بستگی دارد به حالت ورودیها و اینکه ورودیها در چند لحظه قبل چطور تغییر کردهاند. ما در این نوشته بیشتر به مدارهای منطقی ترکیبی شامل چندین گیت منطقی پرداختیم. اما در جدول زیر میتوانید بهطور خلاصه مشاهده کنید که انواع دیگر مدارهای منطقی چیست و چه مثالهایی دارد:
| انواع مدارهای منطقی | |
| مدار ترکیبی | مدار ترتیبی یا مدار حالت |
| خروجی فقط به ورودی در همان لحظه وابسته است. | خروجی به ورودی در همان لحظه و لحظات قبلتر وابسته است. |
| مدارهای منطقی شامل چندین گیت منطقی | فلیپفلاپها |
| نیم جمعکننده و تمام جمعکننده | شیفترجیسترها |
| عملگرهای منطقی مانند مالتیپلکسرها | شمارندهها |
اگر تمایل دارید در مورد منطق ترکیبی اطلاعات دقیقتری کسب کنید، پیشنهاد ما این است که به مطلب «آموزش منطق ترکیبی – مجموعه مقالات جامع وبلاگ فرادرس» مراجعه کنید. در این نوشته مجموعه مطالب منتشر شده از مجله فرادرس که شامل مباحثی مانند مالتیپلکسرها، انکدرها، دیکدرها و جمعکنندههای باینری است، گردآوری شده است. در ادامه راجعبه مدارهای حالت فلیپفلاپ، رجیستر و شمارنده بیشتر توضیح میدهیم.
فلیپفلاپ چیست؟
ابتدا میخواهیم ببینیم «فلیپفلاپ» (Flip-Flop) بهعنوان یک مدارهای حالت از انواع مدار منطقی چیست و چه ویژگیهایی دارد. فیلپفلاپ یک مدار الکترونیکی دیجیتالی یا نوعی مدار منطقی است که در مجموع دارای چهار ورودی و خروجی است. فلیپفلاپها قطعات اصلی ابزارهای الکترونیکی با قابلیت ذخیرهسازی مانند حافظهها محسوب میشوند. علت استفاده از این قطعات در حافظهها این است که این نوع مدار حالت تمایل دارد حالت را حفظ کند، مگر اینکه ورودی بر اساس تغییر حالت تنظیم شود.
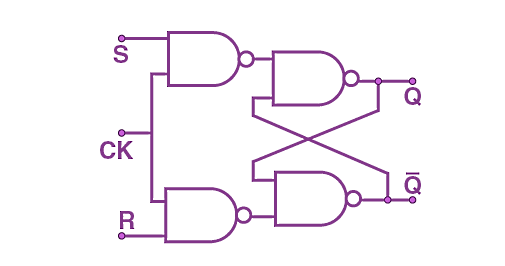
همانطور که مشاهده میکنید یک فلیپفلاپ از چهار گیت منطقی ساخته میشود. انواع فیلپفلاپ عبارت است از:
با رعایت قوانین مشخصی این امکان وجود دارد که بتوانیم انواع فلیپفلاپ را به هم تبدیل کنیم. شکل بالا مدار سادهترین فلیپفلاپ یعنی فلیپفلاپ S - R را نشان میدهد که برای آن جدول صحت مشخصی هم داریم. S - R در این نوع فلیپفلاپ به معنای تنظیم کردن و مجددا تنظیم کردن (Set-Reset) است، در نتیجه دو ورودی S و R و دو خروجی Q و Q بار در این نوع فلیپفلاپ خواهیم داشت (Q بار با Q برابر نیست).
روش کار این فلیپفلاپ به این صورت است که وقتی S یا ورودی Set روشن میشود، خروجی Q برابر است با یک در حالی که با روشن شدن R یا ورودی Reset، خروجی Q برابر با صفر میشود. همچنین اگر هر دوی S و R برابر با صفر باشند، فلیپفلاپ آخرین حالت خود را حفط خواهد کرد. همچنین نکته مهم در مورد فلیپفلاپ این است که از این نوع مدار حالت برای ذخیرهسازی یک تک بیت یعنی صفر یا یک استفاده میشود. بنابراین اگر بخواهیم بیتهای بیشتری از دادهها را ذخیره کنیم، نیاز داریم از چند فلیپفلاپ استفاده کنیم.
رجیستر چیست؟
رجیسترها گروهی از فلیپفلاپها هستند که برای ذخیرهسازی چند بیت از دادهها بهصورت سری به هم متصل شدهاند. با توجه به اینکه گفتیم فلیپفلاپ اطلاعات را فقط در یک بیت ذخیره میکند، اگر بخواهیم چند بیت داده را ذخیره کنیم باید از مدار حالتی به نام رجیستر استفاده کنیم. به این ترتیب، انتقال داده از یک فلیپفلاپ به فلیپفلاپ دیگر «شیفت رجیستر» (Shift Register) نامیده میشود.
شمارنده چیست؟
تا اینجا یاد گرفتیم که نوع ترتیبی یک مدار منطقی چیست و با انواع مدارهای منطقی ترتیبی یا مدار حالت مانند فلیپفلاپ و رجیستر آشنا شدیم. اگر مدار منطقی ما متشکل از چند فلیپفلاپ متصل شده بهصورت سری باشد که برای شمارش تعداد ورودیها بکار میروند، در این صورت این مدار حالت شمارنده یا Counter نام دارد. بر اساس نوع فیلپفلاپی که در شمارنده استفاده شده است، میتوانیم شمارندهها را به دو گروه «سنکرون» (Synchronous) و «آسنکرون» (Asynchronous) تقسیمبندی کنیم.
گیت منطقی چیست؟
در بخشهای قبل تا حدی یاد گرفتیم که تعریف مدار منطقی چیست. در این بخش میخواهیم به معرفی واحد سازنده این مدارها، یعنی گیت منطقی بپردازیم. عملکرد گیت منطقی بر مبنای جبر بولی است و از مهمترین مفاهیم در الکترونیک بهشمار میرود. گیتهایی که در ادامه معرفی میشوند اغلب در مداریی مانند ترموستاتهای ایمنی، قفلهای دکمهای، سیستمهای آبیاری خودکار، دزدگیرهای نورفعال و بسیاری از وسایل الکترونیکی دیگر بکار میروند.
گیتهای منطقی پس از دریافت یک یا چند ورودی دو حالته یا باینری، عملیات پردازش روی آنها انجام داده و یک خروجی دو حالته یا باینری را بر اساس عمل منطقی که برای آنها تعریف شده است، تولید میکنند. بنابراین این اجزا مولفه ضروری مدارهای دیجیتالی هستند. گیتهای منطقی استاندارد عبارتاند از:
- گیت OR
- گیت AND
- گیت NOT

هر کدام از این گیتها یک عمل منطقی خاصی را انجام میدهند. برای مثال، در جدول زیر عملیات منطقی خاص گیت منطقی AND نمایش داده شده است. همچنین مشخص شده است که ورودیهای ممکن و خروجی نهایی این گیت در مدار منطقی چیست.
| ورودی A | ورودی B | خروجی (A AND B) |
به چنین جدولی جدول درستی یا جدول صحت گیت منطقی گفته میشود. استفاده از این جداول یک روش مرسوم و جامع است برای نشان دادن این موضوع که چگونه ورودیهای دو حالتی میتوانند روی خروجی یک گیت منطقی و در نتیجه روی کل مدار منطقی تاثیرگذار باشند. در مطالعه جداول درستی برای یک مدار منطقی یا در مورد یک گیت منطقی، هر ستون از جدول نشاندهنده یک ورودی یا خروجی است. همچنین هر ردیف توصیف کننده یک حالت از ورودیهای ممکن است که با خروجی مناسب متناظر شده است. اهمیت جداول صحت در دنیای الکترونیک دیجیتال به دلایل زیر است:
- این جداول میتوانند عملکرد یک گیت منطقی را در تمام حالتها نشان داده و اعتبار ببخشند.
- آنها میتوانند خلاصهای از تمام حالتهای ممکن برای یک سیستم دیجیتالی را ارائه دهند.
- در طراحی مدارهای منطقی بسیار مفیداند، چون دید کلی از نحوه عملکرد مدار ارائه میدهند.
برای اینکه جدول صحت را برای یک گیت منطقی رسم کنیم، کافی است مراحل زیر را قدم به قدم اجرا کنیم:
- تعداد ستونها با تعداد ورودیهای مدار منطقی برابر است. همچنین یک ستون در انتهای جدول برای تک خروجی گیت در نظر میگیریم.
- تعداد ردیفهای این جدول باید برابر با باشد که در آن n تعداد ورودیها است. برای مثال اگر دو ورودی داریم، ردیف خواهیم داشت.
- داخل جدول را با حالتهای مختلفی که برای ورودیها ممکن است داشته باشیم، پر میکنیم.
- خروجی بر اساس عملکرد منطقی گیت تعیین میشود که در سلول مربوط به هر ترکیب از ورودیها درج خواهد شد.
عمل منطقی گیتهای مختلف با هم متفاوت است. در کابرد، اغلب گیتهای منطقی را در کنار هم و بهصورت ترکیبی میبینید. برای مثال گیت XOR، گیت NAND، گیت NOR، گیت EXOR و گیت XNOR از جمله گیتهایی هستند که بر اساس گیتهای استاندارد که بالاتر معرفی کردیم، ساخته میشوند. بنابراین یکی از مزایای گیتهای منطقی این است که میتوانیم بسته به عملکرد موردانتظار خود، ترکیبات مختلفی از آنها در مدار داشته باشیم. هیچ محدودیتی برای تعداد گیتهای مورد استفاده در مدار وجود ندارد، بهجز ابعاد و فضای قطعهای که مدار را برای آن طراحی میکنیم.
انواع گیتهای منطقی
در این بخش عمل منطقی مختص هر کدام از گیتهای منطقی را به همراه جدول صحت، عبارت بولی، نماد و ورودیها و خروجی نهایی هر گیت کاملا توضیح میدهیم تا بهتر متوجه شوید تفاوت بین گیتهای مختلف در یک مدار منطقی چیست. اما پیش از پرداختن به معرفی انواع گیتهای منطقی، اگر به درس مدار منطقی تسلط کافی ندارید و میخواهید مباحث مربوطه را به صورت کامل و با جزئیات و مثالهای تئوری و عملی، فرا بگیرید، پیشنهاد ما این است که فیلم آموزش مدار منطقی – مرور و حل مساله فرادرس را مشاهده کنید. لینک این دوره آموزشی در ادامه برای شما قرار داده شده است:
گیت OR
ابتدا میخواهیم ببینیم که گیت پایه OR برای انجام چه نوع عملی طراحی شده است و کاربرد آن در یک مدار منطقی چیست. یک گیت OR دو ورودی دارد و بر این اساس کار میکند که اگر یک یا هر دو ورودی آن یک باشد، خروجی هم یک خواهد بود. شکل زیر نماد این گیت را نشان میدهد. در سمت چپ تصویر دو ورودی با حروف A و B مشخص شدهاند. در سمت راست تصویر عبارت بولی متناظر با این عمل منطقی نشان داده شده است.
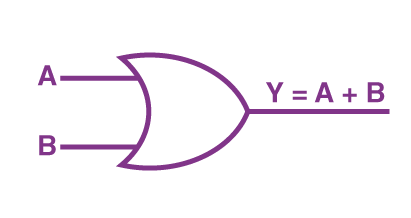
با اینکه عبارت بولی گیت OR بهصورت نوشته میشود، اما نحوه خواندن آن به این شکل است: Y مساوی است با A یا B. در ادامه جدول درستی این گیت را مشاهده میکنید:
| ورودی A | ورودی B | خروجی (A OR B) |
گیت AND
دومین گیت استانداردی که در این بخش با آن آشنا میشویم تا بهتر متوجه شویم نحوه عملکرد یک مدار منطقی چیست، گیت AND است. خروجی گیت AND فقط و فقط در حالتی یک میشود که هر دو ورودی آن یک باشد. در غیر این صورت برای بقیه حالتها همواره خروجی AND برابر با صفر است. برای مثال اگر دو ورودی این گیت را برابر با A و B در نظر بگیریم، حالتی که در آن خروجی یک داریم، به شکل زیر است:
A = ۱ و B = ۱
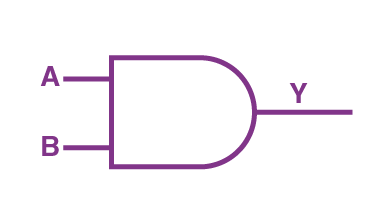
اما در بقیه حالتها شامل موارد زیر خروجی همواره صفر است:
A = ۱ و B = ۰
A = ۰ و B = ۱
A = ۰ و B = ۰
این توضیحات در جدول درستی این گیت که بالاتر معرفی شد، خلاصه شدهاند. عبارت بولی متناظر با عملکرد این گیت به شکل است که در تصویر بالا درج نشده است.
گیت NOT
بر خلاف دو گیت قبل که دارای دو ورودی بودند، گیت NOT فقط یک ورودی دارد. در نتیجه فقط یک تک مقدار را تبدیل میکند. این گیت منطقی تک مقداری ورودی را معکوس میکند، به این معنا که اگر یک بگیرد، صفر تحویل میدهد و اگر صفر بگیرد، یک را بهعنوان خروجی خواهد داد. عبارت بولی متناظر برای گیت NOT بهصورت نوشته میشود و نحوه خواندن آن به این شکل است: Y برابر با A نیست. در ادامه جدول درستی این گیت را نیز میتوانید مشاهده کنید:
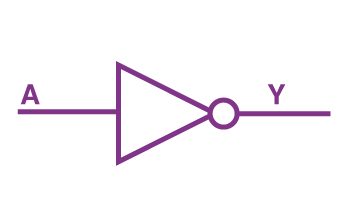
| ورودی A | خروجی Y |
گیت NAND
گفتیم ترکیبات مختلفی از سه گیت بالا منجر به تولید گیتهای منطقی با عملیات جدید خواهند شد. یکی از این گیتهای ترکیبی، گیت NAND است که از ترکیب دو گیت AND و NOT ساخته میشود. این گیت خروجی برابر با صفر ارسال میکند، اگر هر دو ورودی آن یک باشد، اما در مابقی حالتها خروجی آن همواره برابر با یک است. همانطور که در تصویر زیر مشاهده میکنید، علامت دایره کوچک در بخش خروجی نشاندهنده اضافه شدن گیت NOT به AND است:
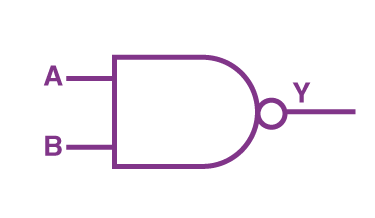
تصویر زیر نشان میدهد که چگونه گیتهای AND و NOT برای ساخت یک گیت NAND با هم ترکیب میشوند. همانطور که مشاهده میکنید، خروجی حاصل از AND بهعنوان ورودی NOT در نظر گرفته میشود:
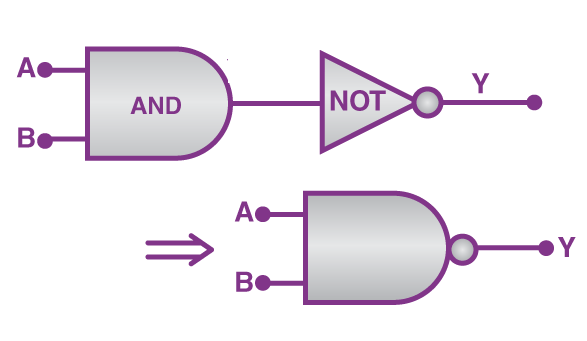
همچنین عبارت بولی معادل با این گیت به شکل نمایش داده میشود. جدول درستی گیت NAND در ادامه آورده شده است:
| ورودی A | ورودی B | خروجی Y |
همچنین میتوانیم بهجای این جدول ابتدا جدول درستی گیت AND را در نظر بگیریم:
| ورودی A | ورودی B | |
سپس مقادیر خروجی آن را معکوس کنیم (با قرار دادن علامت بار که عملکرد منطقی گیت NOT محسوب میشود) تا خروجی NAND حاصل شود. مشاهده میکنید که خروجیهای جدول زیر با خروجی جدول درستی گیت NAND در بالا یکسان است:
گیت NOR
تا اینجا آموختیم که سه گیت اصلی در یک مدار منطقی چیست و با یک گیت ترکیبی نیز آشنا شدیم. دومین گیت ترکیبی در این بخش گیت NOR است که از ترکیب گیتهای OR و NOT ساخته میشود. عملکرد منطقی این گیت به این شکل است که فقط در حالتی که هر دو ورودی برابر با صفر باشند، خروجی یک داریم. در بقیه حالتها خروجی همیشه صفر است.
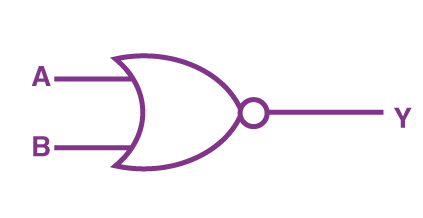
عبارت بولی متناظر با گیت NOR بهصورت است و جدول درستی آن به شرح زیر نوشته میشود:
| ورودی A | ورودی B | خروجی Y |
همچنین در شکل زیر مشخص است که گیتهای OR و NOT برای ساخت گیت NOR چگونه با هم ترکیب میشوند. باز هم گیتی که دو ورودی میپذیرد یعنی OR، ابتدا قرار میگیرد و خروجی آن به گیت NOT ارسال میشود:
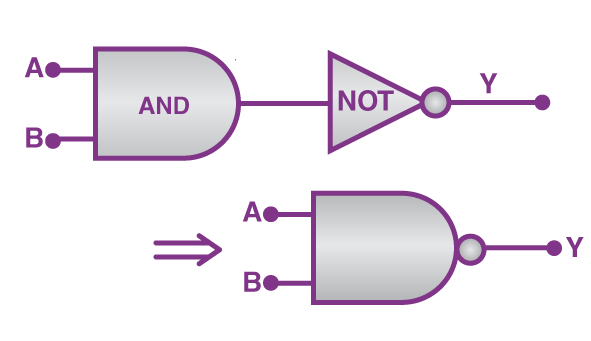
اگر بخواهیم از جدول درستی OR به خروجی جدول بالا در ستون آخر برسیم، کافی است خروجیهای گیت OR را به شکل زیر معکوس کنیم:
گیت XOR
گیت ترکیبی بعدی گیت XOR یا گیت OR حذفی (Exclusive-OR gate) است. خروجی یک گیت XOR با دو ورودی تنها زمانی حالت یک میپذیرد که دو ورودی مشابه هم نباشند، یعنی اگر ورودی A برابر است با یک، ورودی B باید صفر باشد و برعکس. بنابراین در حالتی که هر دو ورودی مشابه هم هستند، خروجی گیت XOR برابر با صفر خواهد شد. حتی اگر بالاترین مقادیر ورودی یعنی یک را داشته باشیم، باز هم در صورت مشابه بودن هر دو ورودی، خروجی صفر است.
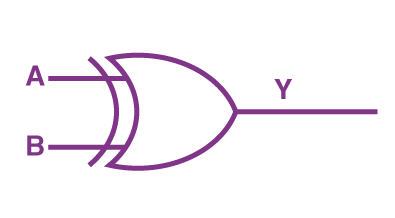
عبارت بولی توصیفکننده عملکرد این گیت معادل است با یا و جدول درستی آن بهصورت زیر است:
| ورودی A | ورودی B | خروجی Y |
برخلاف دو گیت ترکیبی قبل، گیت XOR ترکیبی از سه گیت منطقی زیر است:
XOR = NOT + AND + OR
پس همانطور که در شکل زیر میبینید، نحوه اتصال این گیتها برای ساخت XOR در مقایسه با دو گیت ترکیبی قبل، پیچیدهتر خواهد بود. ابتدا دو ورودی A و B هر کدام به دو گیت NOT (که تک ورودی است) وارد میشوند. معکوس این مقادیر، همراه با ورودی دیگر به دو گیت AND ارسال میشوند. در نهایت خروجیهای حاصل از دو گیت AND به یک گیت OR ارسال میشود. بنابراین در این فرآیند از دو گیت NOT و دو گیت AND استفاده شد، در حالی که فقط یک گیت OR در انتها بکار رفته است. گیت XOR نهایی در تصویر زیر نشان داده نشده است، اما نماد آن در بالا نمایش داده شده است.
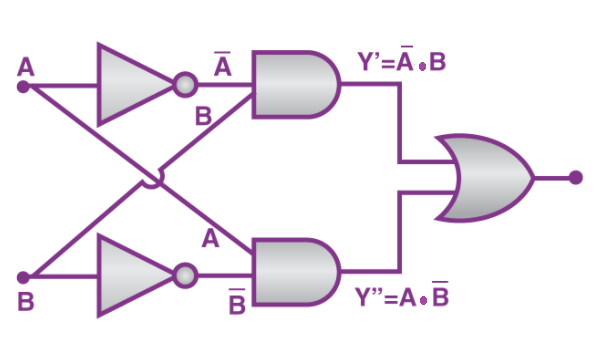
گیت XNOR
در آخرین قسمت از این بخش، عملکرد و مشخصات گیت XNOR یا گیت NOR حذفی (Exclusive-NOR Gate) را توضیح میدهیم تا معرفی انواع گیتها در بخش گیت منطقی چیست و چه انواعی دارد، تکمیل شود . برای این گیت زمانی خروجی یک ارسال میشود که هر دو ورودی یکسان باشند، یعنی هر دو ورودی برابر با یک یا صفر باشند. بنابراین در حالتهایی که ورودیهای یکسان نداریم، مثلا صفر و یک، خروجی گیت XNOR برابر با صفر است.
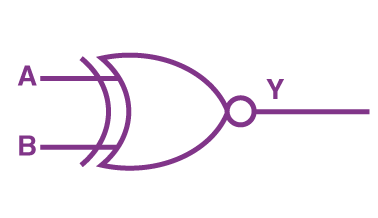
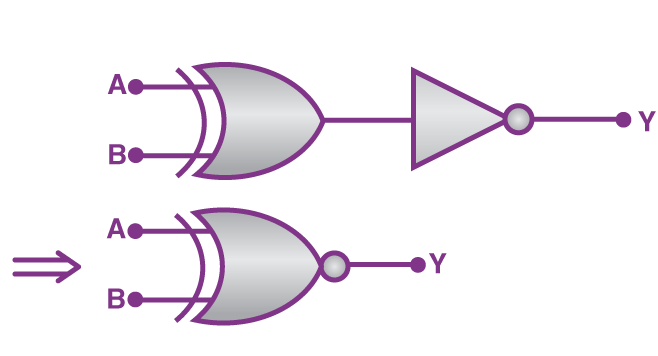
مشاهده میکنید که نماد گیت XNOR کاملا مشابه نماد گیت NOR است، با این تفاوت که در ابتدای آن یک خط منحنی شکل داریم. این خط نشاندهنده حذفی بودن گیت است که در مورد نماد گیت XOR نیز رسم میشود. عبارت بولی توصیفکننده این گیت بهصورت است و جدول درستی آن شامل اطلاعات زیر خواهد بود:
| ورودی A | ورودی B | خروجی Y |
این گیت ترکیبی از یک گیت ترکیبی دیگر یعنی XOR و گیت NOT است. نحوه ترکیب این دو گیت بهصورت زیر است:
قضایای دمورگان
در بخش قبل کاملا یاد گرفتیم که انواع گیت منطقی چیست و بر مبنای چه عمل منطقی طراحی شدهاند. قضایای دمورگان از جمله مهمترین و پرکاربردترین ابزارهای جبر بولی هستند که توسط فردی به نام «آگوستوس دمورگان» (Augustus De Morgan) برای اولین بار مطرح شدند. در ادامه این دو قضیه را توضیح میدهیم.
قضیه اول
اولین قضیه دمورگان توصیفکننده تساوی مهمی است که با عبارت بولی زیر نشان داده میشود:
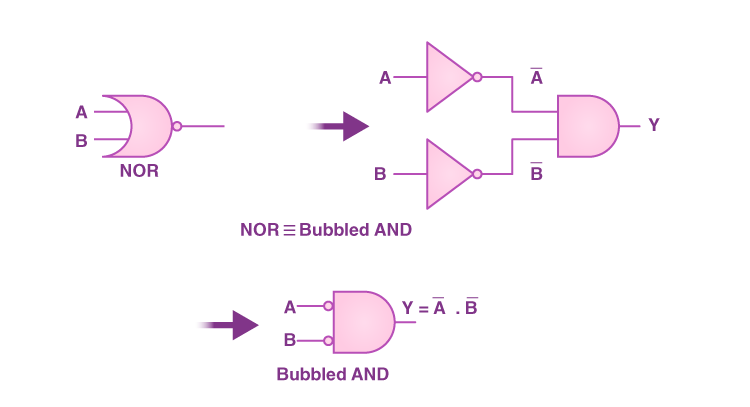
سمت چپ این تساوی بیانگر عبارت بولی متناظر با گیت منطقی NAND با دو ورودی A و B است و سمت راست آن، نمایشدهنده گیت ORای است که معکوس شده است. در بخش قبل گفتیم عبارت بولی گیت OR به شکل است. در نتیجه وقتی عبارتی بهصورت داریم، میتوانیم نتیجهگیری کنیم که این نمایش همان معکوس گیت OR یا Bubbled OR است. پس اولین قضیه دمورگان بیان میکند که عملکرد گیت NAND روی دو ورودی A و B با عملکرد یک گیت معکوس OR روی این دو ورودی معادل است:
NAND = Bubbled OR
تصویر زیر همین توضیحات را روی شکل نشان میدهد. همچنین در ادامه جدولی آورده شده است که درستی اولین قضیه دمورگان را تایید میکند. اگر دقت کنید ستونهای سوم و ششم از سمت راست با هم برابر شدهاند:
| ورودی A | ورودی B | ||||
قضیه دوم
در دومین قضیه دمورگان تساوی دیگری به شکل زیر معرفی میشود:
سمت چپ این تساوی نمایش دهنده گیت NOR با دو ورودی A و B است. این گیت با یک گیت AND معکوس یا Bubbled AND معادل شده است. بنابراین قضیه دوم دمورگان بیان میکند که عملکرد گیت NOR روی دو ورودی A و B معادل است با عملکرد گیت معکوس AND روی همین دو ورودی:
NOR = Bubbled AND
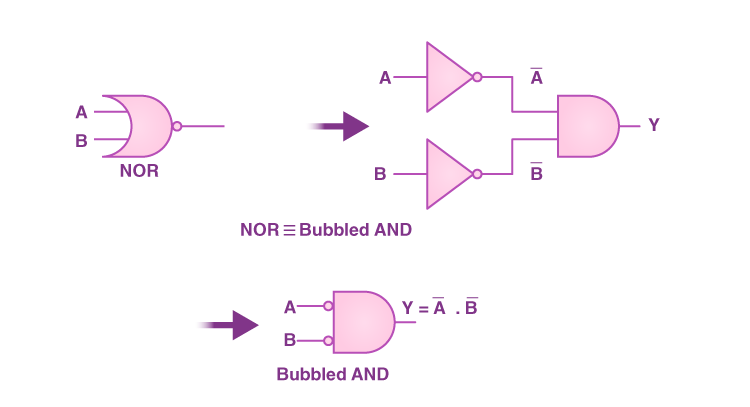
مشاهده میکنید که در جدول زیر مقادیر خروجی حاصل از گیت NOR در سومین ستون از سمت راست با خروجیهای گیت AND معکوس در ششمین ستون کاملا یکسان است. در بخش بعد با حل چند مثال بهتر متوجه خواهید شد که روشهای مختلف ترکیب انواع گیتهای منطقی در یک مدار منطقی چیست.
| ورودی A | ورودی B | ||||
حل مثال و تمرین در مورد گیتهای منطقی
پس از اینکه کاملا یاد گرفتیم مدار منطقی چیست، گیتهای منطقی چه انواعی دارند و چه عملکردی روی ورودیهای داده شده پیاده میکنند، در این بخش با حل چند مثال به شما کمک میکنیم تا یادگیری خود را در این زمینه تکمیل کنید. همچنین در انتهای این قسمت دو تمرین نیز برای شما در نظر گرفته شده است تا با پاسخدهی به آنها مهارت خود را در زمینه تشخیص عملکرد گیتهای منطقی محک بزنید.
مثال ۱
در مدار منطقی زیر، اگر ورودیهای A و B روی یک و ورودی C روی صفر تنظیم شوند، خروجی نهایی کدام است؟
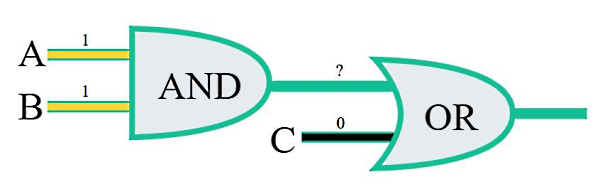
پاسخ
با توجه به اینکه هر دو ورودی گیت AND برابر با یک است، خروجی آن هم یک میشود. این خروجی بهعنوان یکی از ورودیهای گیت OR همراه با ورودی C که روی صفر تنظیم شده است، در نظر گرفته میشوند. خروجی گیت OR در این حالت برابر است با یک، چون حداقل یکی از ورودیهای آن یک است.
مثال ۲
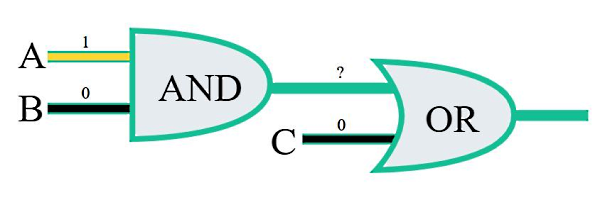
در شکل زیر، خروجی مدار منطقی چیست؟
پاسخ
در این مدار منطقی، ورودی A روی یک تنظیم شده است، در حالی که B متناظر است با صفر. در نتیجه خروجی گیت AND برابر میشود با صفر، چرا که یکی از ورودیهای آن صفر است. بنابراین هر دو ورودی برای گیت OR برابر با صفر خواهد شد و خروجی این گیت نیز صفر میشود، چون هیچ کدام از ورودیهای آن یک نیست.
مثال ۳
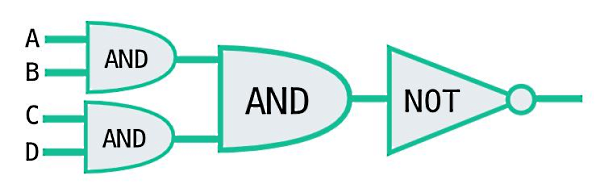
یک مدار منطقی با چهار گیت داریم که در آن خروجی دو گیت AND ابتدایی به گیت AND سوم ارسال میشود. همچنین در انتها یک گیت NOT داریم که خروجی AND به آن وارد میشود. اگر بدانیم خروجی نهایی این مدار صفر است، ورودیهای A و B و C و D چه مقادیری ممکن است داشته باشند؟
پاسخ
میدانیم اگر ورودی گیت NOT برابر با صفر باشد، خروجی آن یک و اگر ورودی آن یک باشد، خروجی صفر است. چون خروجی نهایی ما در این سوال صفر شده است، پس ورودی NOT حتما برابر است با یک. در نتیجه خروجی سومین گیت AND هم برابر است با یک. خروجی AND وقتی یک میشود که هر دو ورودی آن یک باشد. پس خروجی دو گیت دیگر AND هم برابر است با یک. به همین ترتیب ورودیهای هر دو گیت AND در ابتدای مدار باید برابر با یک باشد. بنابراین ورودیهای مدار منطقی ما عبارتاند از:
A = B = C = D = ۱
مثال ۴
نمودار زیر یک مدار منطقی را که متشکل است از سه گیت نشان میدهد، به این صورت که دو خروجی حاصل از دو گیت AND به یک گیت OR ارسال میشوند. بنابراین این مدار شامل چهار ورودی است (A,B,C,D)، که هر دو عدد ورودی برای یک گیت AND تنظیم شده است. اگر خروجی نهایی این مدار یک شود، حالتهای ممکن برای ورودیهای A و B و C و D چیست؟
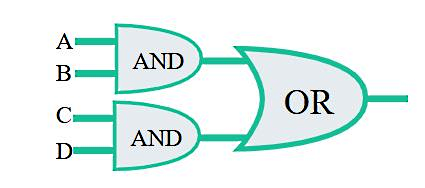
پاسخ
خروجی نهایی از گیت OR حاصل شده است و میدانیم در دو حالت ممکن است خروجی OR برابر با یک شود:
- اگر هر دو ورودی آن یک باشد.
- اگر حداقل یکی از دو ورودی آن یک باشد (بالا یک و پایین صفر یا بالا صفر و پایین یک)
ابتدا حالت اول را در نظر میگیریم. یک شدن هر دو ورودی OR میتواند به این معنا باشد که خروجی هر دو گیت AND برابر با یک شده است. برای اینکه خروجی یک گیت AND مساوی با یک شود، باید هر دو ورودی آن یک باشد. پس در این حالت لازم است داشته باشیم:
A = B = C = D = ۱
حالا میرویم سراغ حالت دوم. فرض کنید خروجی گیت AND بالا برابر با یک و خروجی گیت AND پایین برابر با ۰ است. در این صورت برای گیت AND بالایی ورودیها باید حتما به شکل A = B = ۱ باشند. این در حالی است که برای گیت AND پایینی، یکی از حالتهای زیر ممکن است:
C = ۱ و D = ۰
C = ۰ و D = ۱
بنابراین یکی از دو حالت زیر ممکن است:
A = B = C = 1 و D = 0
A = B = D = 1 و C = 0
همچنین در حالت دوم ممکن است خروجی گیت AND بالا صفر باشد، اما گیت پایین خروجی یک دهد. در این حالت در مورد گیت AND پایین حتما دو ورودی برابر است با یک، یعنی داریم:
C = D = ۱
اما در مورد گیت بالایی با خروجی صفر، یکی از دو حالت زیر را خواهیم داشت:
B = ۱ و A = ۰
A = ۱ و B = ۰
بنابراین ورودیهای ممکن برای این حالت به شکل زیر است:
B = C = D = ۱ و A = ۰
A = C = D = ۱ و B = ۰
در مجموع لیست زیر نشان میدهد ورودیهای ممکن برای این مدار منطقی با خروجی نهایی یک کداماند:
A = B = C = D = ۱
A = B = C = ۱ و D = ۰
A = B = D = ۱ و C = ۰
B = C = D = ۱ و A = ۰
A = C = D = ۱ و B = ۰
مثال ۵
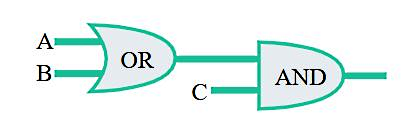
یک مدار منطقی داریم که در آن خروجی گیت OR معادل است با یکی از ورودیهای گیت AND. این مدار سه ورودی با نام A و B و C دارد. اگر بدانیم خروجی نهایی آن و ورودی C برابر با یک است، ورودیهای A و B چه مقادیری میتوانند داشته باشند؟
پاسخ
با توجه به اینکه خروجی نهایی گیت AND برابر با یک شده است و میدانیم یکی از ورودیهای این گیت یعنی C برابر با یک است، در نتیجه باید ورودی دیگر این گیت هم یک باشد. این ورودی معادل است با خروجی گیت OR. پس تا اینجا به این نتیجه رسیدیم که خروجی OR برابر است با یک. برای اینکه چنین خروجی از OR بگیریم، ممکن است یکی از سه حالت زیر اتفاق بیفتد:
- A = B = ۱
- A = ۱ و B = ۰
- A = ۰ و B = ۱
تمرین ۱
تمرین ۲
مشخصه گذار یک گیت منطقی چیست؟
پس از اینکه در بخش گذشته یاد گرفتیم انواع مدار منطقی چیست، در این بخش به پاسخ دادن به این سوال میپردازیم که در یک گیت منطقی دقیقا در چه زمانی صفر به یک تبدیل میشود؟ یا دقیقا در چه ولتاژی یک مدار منطقی تصمیم میگیرد که ورودی دیگر صفر نباشد و یک باشد؟ برای اینکه بتوانیم به این سوالات پاسخ دهیم، بهتر است با مفهومی به نام مشخصه گذار یک گیت منطقی آشنا شویم.
عموما برای تست کردن مدار منطقی به شیوهای امن و کمخطر، از مقادیر صفر ولتاژ بهعنوان صفر دیجیتال استفاده میکنیم. اما برای مثال، در مورد یک مدار منطقی نوعی به شکل زیر که با یک منبع تغذیه میشود، عموما ولتاژهای زیر معادل صفر و هر مقدار بالای معادل با یک در نظر گرفته میشود. این مدار را میتوانیم بهعنوان مداری برای بررسی نقطه دقیق گذار از صفر به یک در یک گیت منطقی در نظر بگیریم.
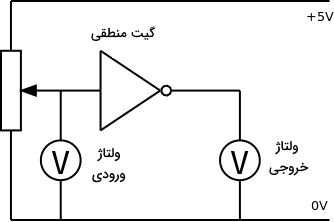
در این مدار، پتانسیومتر ولتاژ ورودی متغیری را به مدار میدهد که این ولتاژ توسط ولتمتر و بهعنوان ورودی اندازهگیری میشود. ولتمتر دوم نیز ولتاژ خروجی از گیت منطقی را اندازه میگیرد. نموداری که بر اساس مدار بالا میتوان رسم کرد و نشاندهنده تغییرات ولتاژ خروجی با ولتاژ ورودی است، مشخصه گذار گیت منطقی نام دارد. این نمودار نشان میدهد که ولتاژهای ورودی و خروجی چه ارتباطی با هم دارند. با توجه به مدار بالا، انتظار داریم نمودار ما مشخصه نوعی یک گیت منطقی NOT را نمایش دهد. بنابراین مشخصه گذار برای گیتهای مختلف متفاوت است و هر گیت منطقی مشخصه گذار خودش را دارد.
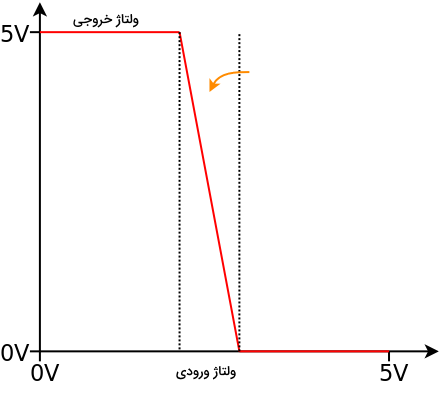
طبق فرضیاتی که در ابتدای بخش در نظر گرفتیم، میخواهیم مشخصه گذار گیت منطقی NOT به شکل بالا را تحلیل کنیم. گفتیم با توجه به منبع تغذیه در این مدار، دو بازه مختلف را برای ورودی تعریف میکنیم:
- ولتاژ ورودی زیر معادل است با صفر.
- ولتاژ ورودی بالای معادل است با یک.
در حالت اول، یعنی زمانی که ولتاژ ورودی زیر است، ورودی گیت NOT معادل است با صفر. میدانیم عمل منطقی گیت NOT روی هر ورودی، معکوس کردن آن است. پس خروجی گیت NOT در بازه ولتاژ ورودی زیر برابر است با یک. وقتی که ولتاژ بین و قرار دارد، خروجی تعریف مشخصی نخواهد داشت، یعنی خروجی برای این بازه نه صفر منطقی است و نه یک منطقی. اما برای ولتاژهای ورودی بالاتر از ، خروجی قطعا متناظر است با صفر. در این بازه ورودی گیت NOT معادل است با یک که در نتیجه عمل معکوس کردن، خروجی صفر ارسال خواهد شد.
مسیر یادگیری الکترونیک با فرادرس
همانطور که اشاره کردیم، کاربرد مدارهای منطقی در ساخت قطعات الکترونیکی است. بنابراین در این بخش قصد داریم چند فیلم آموزشی با موضوع الکترونیک به شما معرفی کنیم. مشاهده این دورههای آموزشی به شما کمک میکند درک عمیقتری نسبت به مدارهای الکترونیکی بهدست بیاورید. یادگیری این مباحث به شما کمک میکند تا بهتر متوجه شوید که تفاوت انواع مدارهای الکترونیکی با مدار منطقی چیست.
- فیلم آموزش مدارهای الکتریکی ۱ فرادرس
- فیلم آموزش مدارهای الکتریکی ۲ فرادرس
- فیلم آموزش الکترونیک ۱ فرادرس
- فیلم آموزش الکترونیک ۲ فرادرس
- فیلم آموزش مبانی الکترونیک دیجیتال ۱ فرادرس
مقاومتهای پول آپ و پول داون
در بخشهای قبل توضیح دادیم که معنای دیجیتال یا باینری بودن ورودیها و خروجیها در یک مدار منطقی چیست. در این بخش قصد داریم ببینیم ورودیها چگونه به یک مدار منطقی ارسال میشوند. اگر ورودی که به یک مدار منطقی داده میشود، خروجی مدار منطقی دیگری باشد، مشکلی نخواهیم داشت. چون این ورودی حتما به فرمت دیجیتالی یعنی صفر یا یک منطقی است. اما اگر بخواهیم از کلید یا Switch بهعنوان ورودی استفاده کنیم، ابتدا باید مطمئن شویم که تمام سیمها بهخوبی متصل شدهاند.
علت این است که از نظر فنی سیمهایی که بهدرستی متصل نشدهاند یا قطع هستند، ورودیهایی به نام شناور یا floating ایجاد میکنند. شناور نوعی ورودی است که به هیچ جای مشخصی متصل نباشد و هیچ منطق صفر یا یکی ندارد. به همین منظور از مقاومتهای پولآپ و پولداون (Pull-up and Pull-down Resistors) در مدار منطقی استفاده میشود. استفاده از مقاومتهای پولآپ و پولداون به ما اطمینان میدهد که ورودی مدار منطقی ما حتما به چیزی متصل است و شناوری نداریم. عموما اندازه این مقاومتها برابر است با اما مقادیر این مقاومتها در بازه تا میتواند قرار بگیرد.
شکلهای زیر نحوه کاربرد مقاومتهای پولآپ و پولداون را در مدار منطقی را نشان میدهند. برای مثال در اولین تصویر بخشی از یک مدار نشان داده شده است که در آن زمانی که کلید فشار داده نشده است، مدار منطقی از طریق مقاومت به ولتاژ صفر متصل است. در این حالت ورودی مدار منطقی معادل است با صفر. اما اگر کلید فشار داده شود، مدار منطقی مستقیما به پایانه مثبت منبع متصل میشود. در این صورت ورودی مدار یک است.
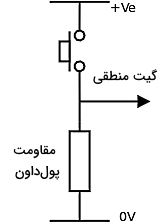
لزوم استفاده از مقاومت پولداون در این بخش از مدار این نکته است که با فشار دادن کلید، پایانه مثبت منبع تغذیه مستقیما به ولتاژ صفر وصل نمیشود و در نتیجه اتصال کوتاه نخواهیم داشت. به همین ترتیب در شکل بعد، اگر کلید را فشار ندهیم، مدار منطقی ما از طریق مقاومت پولآپ به پایانه مثبت منبع وصل میشود. در نتیجه ورودی آن یک است.
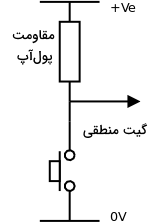
اما با فشار دادن کلید، مدار منطقی ما مستقیما به ولتاژ صفر متصل میشود. در نتیجه ورودی مدار منطقی میشود صفر. در اینجا هم ضرورت استفاده از مقاومت پولآپ در جلوگیری از اتصال کوتاه شدن است. چون با فشار دادن کلید و نبود این مقاومت، پایانه مثبت منبع به ولتاژ صفر وصل شده و اتصال کوتاه خواهیم داشت.
جمعبندی
در این مطلب از مجله فرادرس آموختیم مدار منطقی چیست، بر چه مبنایی کار میکند و چه انواعی دارد. اصول کار یک مدار منطقی بر پایه جبر بولی و منطق دوتایی یا باینری است، یعنی ورودیها و خروجیها در این نوع مدارهای دیجیتالی فقط میتوانند یکی از دو مقدار صفر یا یک را بپذیرند. همچنین یاد گرفتیم واحد اصلی سازنده یک مدار منطقی، گیت منطقی نام دارد. گیتهای منطقی پایه عبارتاند از گیت OR، گیت AND و گیت NOT. سایر گیتها از ترکیب این گیتهای استاندارد ساخته میشوند. در حالت کلی خروجی مدار منطقی به ورودی آن بستگی دارد. اگر مدار منطقی از نوع مدار منطقی ترکیبی باشد، خروجی فقط به ورودی در همان لحظه وابسته است. اما اگر مدار منطقی از نوع ترتیبی یا مدار حالت باشد، تاریخچه ورودیها مهم است.












