مجموعه توانی چیست؟ — از صفر تا صد

در ریاضیات، مجموعه توانی (Power Set) برای یک مجموعه مانند $$S$$ شامل همه زیر مجموعه‌های آن است. البته از آنجایی که خود $$S$$ و مجموعه تهی، زیر مجموعه‌های ذاتی $$S$$ محسوب می‌شوند، آن‌ها را هم در مجموعه توانی منظور می‌کنند. مجموعه توانی نقش مهمی در ریاضیات و بخصوص نظریه مجموعه (Set Theory) و آنالیز ریاضی دارد. به همین دلیل در این نوشتار به مجموعه توانی و خصوصیات آن پرداخته‌ایم. هر چند مفهوم مجموعه توانی، ساده به نظر می‌رسد، ولی یکی از مفاهیم پایه برای مجموعه‌ها است.

به منظور آشنایی بیشتر با مجموعه‌ها و خصوصیات آن‌ها بهتر است به عنوان مقدمه نوشتارهای دیگر مجله فرادرس با موضوع مرتبط با مجموعه توانی را بخوانید. در این میان خواندن مطالب مجموعه متناهی و نامتناهی — تعاریف و خصوصیات و عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده توصیه می‌شود. همچنین مطالعه نوشتارهای مجموعه ها در ریاضیات – مفاهیم پایه و اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده نیز خالی از لطف نیست.

مجموعه توانی

همانطور که در ابتدای متن بیان شد، «مجموعه توانی» (Power Set) یک مجموعه است که اعضای آن باز هم مجموعه هستند، بطوری که هر عضوی، یک زیر مجموعه از مجموعه اصلی است. بنابراین اگر $$S$$ را یک مجموعه در نظر بگیریم و مجموعه توانی آن را به صورت $$P(S)$$‌ مشخص کنیم، می‌توان گفت که $$P(S)$$ از همه زیرمجموعه‌های ممکن مجموعه $$S$$ تشکیل شده است. این موضوع را به بیان ریاضی به صورت زیر نشان می‌دهیم.

$$\large P(S) = \{ A , A \subset S \}$$

فیلم آموزش آمار و احتمال – پایه یازدهم در فرادرس

کلیک کنید

به این ترتیب، هر عضوی از مجموعه توانی $$P(S)$$ یکی از زیرمجموعه‌های $$S$$ است.

نکته: $$A$$ را زیر مجموعه $$B$$ می‌نامند اگر هر عضوی از $$A$$ در $$B$$ وجود داشته باشد. بنا بر تعریف ارائه شده، مشخص است که هر مجموعه‌ای، زیر مجموعه خودش هست. از طرفی با کمک گزاره‌های شرطی و استلزام منطقی واضح است که مجموعه تهی ($$\emptyset$$) نیز زیر مجموعه هر مجموعه‌ای است.

با توجه به نکته گفته شده، دو مجموعه $$S$$ و تهی اعضای بدیهی مجموعه توانی هستند. به عنوان مثال اگر مجموعه $$S$$ را به همراه اعضایش مانند رابطه زیر تعریف کنیم:

$$\large S = \{x,y,z\}$$

آنگاه همه زیرمجموعه‌های ممکن آن به شکل زیر نوشته خواهند شد.

• مجموعه تهی ($$\emptyset$$)
• زیرمجموعه‌های تک عضوی ($$\{x\} , \{y\}, \{z\}$$).
• زیرمجموعه‌های دو عضوی ($$\{x,y\} , \{x,z\} , \{y,z\}$$).
• زیرمجموعه‌های سه عضوی ($$\{x,y,z\}$$ که همان مجموعه $$S$$ محسوب می‌شود.

در این صورت رابطه زیر برقرار خواهد بود.

$$\large P(S) = \{ \{\} , \{x\}, \{y\}, \{z\} , \{x,y\} , \{x,z\}, \{y,z\} , \{x,y,z\}\}$$

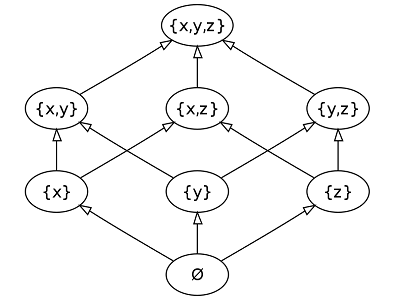
در تصویر زیر اعضای مجموعه توانی را به ترتیب تعداد اعضا مشخص کرده‌ایم. در بالای نمودار، مجموعه $$S$$ و در انتها یا پایین نمودار نیز $$\emptyset$$ دیده می‌شود. مجموعه‌های پایینی در این نمودار با اجتماع با یکدیگر، مجموعه‌های بالایی را می‌سازند. جهت فلش‌ها گویای این مسئله است.

خصوصیات مجموعه توانی

اگر مجموعه $$S$$، یک «مجموعه متناهی» (Finite Set) باشد و تعداد اعضای آن را $$n$$ بنامیم، آنگاه تعداد اعضای مجموعه توانی $$S$$ که با $$|P(S)|$$ نشان داده می‌شود و برابر است با:

$$\large |S| = n , \rightarrow |P(S) |= 2^{n}$$

فیلم آموزش ریاضیات گسسته – پایه دوازدهم در فرادرس

کلیک کنید

این امر را به صورت گزاره زیر می‌توان توجیه و بیان کرد.

ابتدا همه عناصر $$S$$ را به شکل دلخواهی مرتب می‌کنیم. هر زیر مجموعه‌ای از $$S$$ را براساس عناصر مجموعه $$\{\gamma_1,\gamma_2,\ldots,\gamma_n\}$$ می‌نویسیم که در آن $$\gamma_i$$ مقدار صفر یا یک را می‌گیرد. توجه دارید که برای $$1 \leq i \leq n$$ مقدار یک را به $$\gamma_i$$ نسبت می‌دهیم اگر عضو $$i$$ام از مجموعه مرتب شده در زیرمجموعه مورد نظر حضور داشته باشد. در غیر اینصورت، مقدار صفر را برایش در نظر می‌گیریم. از آنجایی که تعداد حالت‌هایی که می‌توان چنین مجموعه‌ای را ساخت برابر با $$2^n$$‌ است، تعداد اعضای مجموعه توانی $$S$$ نیز برابر با $$2^n$$ خواهد بود.

نکته: از آنجایی که مجموعه تهی یکی از زیرمجموعه‌های $$S$$ در نظر گرفته شده، تعداد زیرمجموعه‌های غیر تهی $$S$$ را $$2^n - 1$$ محاسبه می‌کنند.

«عناصر قطری کانتور» (Cantor's Diagonal Argument) نشان می‌دهد که مجموعه توانی یک مجموعه (چه متناهی یا نامتناهی) دارای عدد اصلی یا کاردینالتی بزرگتر از خود مجموعه است. به شکل ساده‌تر می‌توان این گزاره را نشانگر بزرگتر بودن مجموعه توانی از خود مجموعه دانست.

همچنین «قضیه کانتور» (Cantor Theorem) نشان می‌دهد که مجموعه توانی یک مجموعه شمارش‌پذیر نامتناهی، مجموعه‌ای نامتناهی ولی شمارش‌ناپذیر است. بنابراین مجموعه توانی مجموعه اعداد طبیعی (Natural Numbers)، دارای یک رابطه یک به یک و پوشا ( one-to-one correspondence) با مجموعه اعداد حقیقی (Real Numbers) است.

مجموعه توانی برای مجموعه $$S$$ به همراه اجتماع (Union) و اشتراک (Intersection) و متمم‌گیری (Complement)، می‌تواند یک الگو برای جبر بول (Boolean Algebra) ایجاد کند.

مجموعه توانی برای مجموعه $$S$$، یک «گروه آبلی» (Abelian Group) است زمانی که عملگر را به صورت تفاضل متقارن (symmetric difference) در نظر بگیریم. به این ترتیب مجموعه تهی، عضو خنثی و هر مجموعه نیز معکوس خودش خواهد بود. همچنین عملگر اشتراک نیز باعث بوجود آمدن خاصیت جمع‌پذیری با پخشی خواهد شد. به این ترتیب، به کمک خاصیت پخشی، می‌توان نشان داد که مجموعه توانی به همراه عملگرهای یاد شده، تشکیل یک «حلقه بولی» (Boolean Ring) را می‌دهد.

بیان مجموعه توانی به عنوان یک تابع

معمولا برای نمایش تمامی توابع از $$Y$$ به $$X$$ از نماد $$X^Y$$ استفاده می‌کنند. به این ترتیب اگر عدد ۲ را براساس نمایش اعداد طبیعی (Natural Number) به صورت $$\{0,1\}$$ نشان دهیم، آنگاه همه توابعی که از $$S$$ به ۲ وجود دارند به شکل $$\{0,1\}^s$$ نوشته می‌شوند.

فیلم آموزش ریاضیات گسسته – جامع و به زبان ساده در فرادرس

کلیک کنید

به کمک شناسایی توابعی که از «پیش-تصویر» (Preimage) عدد ۱ در $$\{0,1\}$$ روی $$S$$ ساخته می‌شوند می‌توان یک تناظر یک به یک و پوشا بین مجموعه توانی $$S$$ یعنی $$P(S)$$ با $$2^S$$ ساخت.

از نمادی که در بالا به آن اشاره کردیم برای شرح یک مثال استفاده می‌کنیم. فرض کنید $$s=\{X,Y,Z\}$$ باشد. می‌خواهیم نشان دهیم که بین اعداد دو دویی از صفر تا $$2^n-1$$ یک «همریختی» (Isomorphism) وجود دارد. یه این معنی که رابطه‌ای یک به یک و پوشا بین آن‌ها قابل تعریف است. توجه داشته باشید که در اینجا $$n$$ تعداد عناصر مجموعه $$S$$ است.

رقم ۱ در هر یک از زیرمجموعه‌های $$S$$، نشانگر مکان در مجموعه فهرست شده $$\{(x,0),(y,1),(z,2)\}$$‌است. بنابراین مجموعه $$\{x,y\}$$ به شکل $$011_{2}$$ نشان داده می‌شود. توجه داشته باشید که ارقام از راست به چپ، موقعیت را نشان می‌دهند.

چنین نگاشتی از مجموعه $$S$$ به اعداد صحیح، به صورت دلخواه تشکیل شده، به همین دلیل نمایش زیرمجموعه‌های یک مجموعه مانند $$S$$ براساس روش بالا، منحصر به فرد نیست. از طرفی ترتیب قرارگیری عناصر در نمایش یکسان است زیرا می‌دانیم که تغییر در ترتیب عناصر یک مجموعه، باعث افزایش یا کاهش «عدد اصلی» (Cardinality) یک مجموعه نخواهد شد.

نکته: البته توجه داشته باشید که این گونه نمایش دو-دویی برای مجموعه $$S$$ فقط در حالتی که این مجموعه شمارا (enumerated) باشد، امکان پذیر است. حتی ممکن است که این مجموعه دارای عدد اصلی بی‌نهایت مانند مجموعه‌های اعداد طبیعی و گویا باشد، ولی نمی‌توان از این شیوه نمایش برای زیرمجموعه‌های اعداد حقیقی که ناشمارا هستند، کمک گرفت.

ارتباط مجموعه توانی با قضیه دو جمله‌ای

مجموعه توانی ارتباط نزدیکی با «قضیه دو جمله‌ای» (Binomial Theorem) یا مثلث خیام-پاسکال دارد. به کمک «حساب ترکیبیاتی» (Combinatorials) و عمل ترکیب، می‌توان نشان داد که تعداد زیرمجموعه‌های $$k$$‌ عضوی از یک مجموعه $$n$$‌ تایی برابر است با ترکیب $$k$$ از $$n$$‌ که با نماد $$C(n,k)$$ نشان داده می‌شود. مقدار این ترکیب را با عنوان «ضریب دو جمله‌ای» (Binomial Coefficient) نیز می‌شناسند.

برای مثال یک مجموعه سه عضوی ($$S=\{x,y,z\}$$) را مانند مثال قبل در نظر بگیرید. تعداد زیرمجموعه‌های $$k$$ عضوی آن به صورت زیر مشخص می‌شود.

• $$C(3,0)$$ نشانگر تعداد زیرمجموعه‌های بدون عضو از $$S$$ است که برابر است با ۱. مشخص است که این مجموعه همان $$\emptyset$$ است.
• $$C(3,1)$$ نشانگر تعداد زیرمجموعه‌های تک عضوی از $$S$$ است که برابر است با ۳.
• $$C(3,2)$$ نشانگر تعداد زیرمجموعه‌های دو عضوی از $$S$$ است که برابر است با ۳.
• $$C(3,3)$$ نشانگر تعداد زیرمجموعه‌های سه عضوی از $$S$$ است که برابر است با ۱. باز هم مشخص است که زیر مجموعه سه عضوی از $$S$$، همان مجموعه $$S$$ خواهد بود.

به این ترتیب می‌توانیم تعداد زیرمجموعه‌های $$S$$ را به شکل زیر محاسبه کنیم. توجه داشته باشید که منظور از $$|2^S|$$ همان تعداد زیرمجموعه‌های $$S$$ است. همچنین نماد $${ x \choose y }$$ بیانگر ترکیب $$y$$ از $$x$$ است.

$$\large {\displaystyle \left|2^{S}\right|=\sum _{k=0}^{|S|}{\binom {|S|}{k}}}$$

که در آن $$|S|$$ نشانگر تعداد اعضای مجموعه $$S$$ است. به این ترتیب اگر $$|S|=n$$ باشد، آنگاه رابطه زیر برقرار است.

$$\large {\displaystyle \left|2^{S}\right|=2^{n}=\sum _{k=0}^{n}{\binom {n}{k}}}$$

الگوریتم پیدا کردن مجموعه توانی

در ادامه این متن به بررسی الگوریتمی برای پیدا کردن زیرمجموعه‌های یک مجموعه خواهیم پرداخت تا به کمک آن مجموعه توانی را تولید کنیم.

فیلم آموزش ریاضیات گسسته – حل تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

ورودی این الگوریتم، یک بردار عددی است که بیانگر یک مجموعه است. توجه دارید که در یک مجموعه عضو تکراری وجود ندارد در نتیجه بردار یاد شده، شامل مقادیر تکراری نیست. خروجی و هدف از اجرای این الگوریتم، پیدا کردن تمامی مجموعه‌هایی است که می‌توانیم از ترکیب کردن این اعداد بسازیم.

نکته: توجه دارید که منظور از ترکیب، قرار دادن اعداد در کنار یکدیگر بدون در نظر گرفتن ترتیب آن‌ها است. به این ترتیب برای مثال مجموعه $$\{1,2,3\}$$ با $$\{3,2,1\}$$ یکسان تلقی خواهد شد.

1input set = [1, 2, 3]
2power set = [[], [1], [2], [3], [1, 2], [2, 3], [1, 3] [1, 2, 3]]

بنابراین مجموعه توانی (Power Set) شامل همه ترکیب‌های این اعداد در نظر گرفته می‌شود. بدیهی است که مجموعه تهی و مجموعه اصلی نیز از اعضای مجموعه توانی خواهند بود.

از آنجایی که تعداد اعضای مجموعه توانی برای مجموعه‌ای به تعداد اعضای $$N$$ برابر با $$2^N$$ است، باید الگوریتم را به تعداد اعداد صفر تا $$2^N$$ تکرار کنیم.

1(1) Loop from 0 to 2N
2(2) For each number get the binary representation of the number, e.g. 3 = 011
3(3) Determine from the binary representation whether or not to include a number from the set, e.g. 011 = [exclude, include, include]

• گام اول: تکرار مراحل بعدی از صفر تا $$2^N$$. شمارنده از صفر تا $$2^N$$.
• گام دوم: برای هر یک از مقادیر شمارنده در گام قبلی، نمایش باینری (دو-دویی) را محاسبه کن.
• گام سوم: براساس نمایش باینری هر عدد، وجود یا عدم عضو در زیرمجموعه را مشخص کن. (برای مثال 001 نشانگر، [وجود، عدم، عدم]).

برای مثال فرض کنید مجموعه $$A$$ به صورت $$A=\{1,2,3\}$$ مشخص شده باشد. در این صورت داریم:

10 = 000
21 = 001
32 = 010
43 = 011
54 = 100
65 = 101
76 = 110
87 = 111

با توجه به موقعیت هر یک از ارقام ۰ و ۱ در نمایش دو-دویی می‌توانیم حضور یا عدم حضور هر عضو در مجموعه را نمایش دهیم. به این ترتیب این ارقام به شکل زیر زیر مجموعه‌ها را مشخص می‌کنند.

1000 = [exclude, exclude, exclude] = []
2001 = [exclude, exclude, include] = [3]
3010 = [exclude, include, exclude] = [2]
4011 = [exclude, include, include] = [2, 3]
5100 = [include, exclude, exclude] = [1]
6101 = [include, exclude, include] = [1, 3]
7110 = [include, include, exclude] = [1, 2]
8111 = [include, include, include] = [1, 2, 3]

این زیرمجموعه‌ها، تشکیل مجموعه توانی را خواهند داد. در ادامه شبه کد مربوط به ایجاد مجموعه توانی به کمک نمایش دو-دویی معرفی شده است.

1function powerSet(arr) {
2  
3  // the final power set
4  var powers = [];
5  
6  // the total number of sets that the power set will contain
7  var total = Math.pow(2, arr.length);
8  
9  // loop through each value from 0 to 2^n
10  for (var i = 0; i < total; i++) {
11    
12    // our set that we add to the power set
13    var tempSet = [];
14    
15    // convert the integer to binary
16    var num = i.toString(2);
17    
18    // pad the binary number so 1 becomes 001 for example
19    while (num.length < arr.length) { num = '0' + num; }
20    
21    // build the set that matches the 1's in the binary number
22    for (var b = 0; b < num.length; b++) {
23      if (num[b] === '1') { tempSet.push(arr[b]); }    
24    }
25    
26    // add this set to the final power set
27    powers.push(tempSet);
28    
29  }
30  
31  return powers;
32  
33}
34
35powerSet([1, 2, 3]);

به این ترتیب اگر از زبان برنامه‌نویسی $$R$$ برای پیاده‌سازی الگوریتم کمک بگیریم، قطعه کدی به شکل زیر خواهیم داشت.

1powerset <- function(set){
2	ps <- list()
3	ps[[1]] <- numeric()						#Start with the empty set.
4	for(element in set){						#For each element in the set, take all subsets
5		temp <- vector(mode="list",length=length(ps))		#currently in "ps" and create new subsets (in "temp")
6		for(subset in 1:length(ps)){				#by adding "element" to each of them.
7			temp[[subset]] = c(ps[[subset]],element)
8		}
9		ps <- c(ps,temp)						#Add the additional subsets ("temp") to "ps".
10	}
11	ps
12}

فیلم آموزش محاسبات عددی و آماری با برنامه نویسی در R – مقدماتی در فرادرس

کلیک کنید

خلاصه و جمع‌بندی

نظریه مجموعه‌ها (Set Theory) و مسائل وابسته به آن یکی از زیباترین بخش‌های ریاضیات محسوب می‌شود که پرسابقه‌ترین شاخه ریاضیات نیز هست. البته در بعضی از مواقع، مفاهیم انتزاعی و قضیه‌های بسیار پیچیده‌ای نیز برای توصیف رفتارهای ساده مجموعه‌ها به کار می‌رود که باعث شده دانشجویان به ندرت به سمت مطالعه این نظریه بروند. دسته مطالب مربوط به نظریه مجموعه‌ها در مجله فرادرس، به منظور ساده‌سازی و روشن‌تر کردن مفاهیم و قضیه‌های نظریه مجموعه‌ها نگاشته می‌شوند.

در این مطلب با تعریف مجموعه توانی و خصوصیات آن آشنا شده و بعضی ویژگی‌های اصلی آن نیز بازگو و مورد بررسی قرار گرفت. همانطور که خواندید، بیان دو-دویی اعداد طبیعی که از تعداد اعضای مجموعه اصلی کوچکتر هستند می‌تواند راه‌کاری برای تولید مجموعه توانی باشد. همچنین در پایان این متن نیز الگوریتم و برنامه‌ای با کد $$R$$ برای استخراج مجموعه توانی نیز معرفی گردید.