مجموعه تهی و علامت تهی چیست؟ + تعریف و حل تمرین و مثال
در آموزشهای پیشین مجله فرادرس با مجموعه و زیرمجموعه آشنا شدیم. همچنین، مطالبی را درباره اجتماع و اشتراک مجموعهها بیان کردیم. در این آموزش، تعریف مجموعه تهی را بیان میکنیم. مجموعهای که هیچ عضوی نداشته باشد مجموعه تهی نامیده میشود. یک مجموعه تهی با علامت ∅ نشان داده میشود و تلفظ آن فی است. برای مثال، مجموعه { } = X مجموعه تهی است.


مجموعههای تهی در مقایسه با مجموعههای دیگر منحصر به فرد در نظر گرفته میشوند. در ادامه این آموزش با مجموعه تهی، تعریف، ویژگیها و مثالهای آن آشنا میشویم.
مجموعه چیست؟
در ریاضیات، «مجموعه» (Set) به گرداورد یا مجموعهای یا دستهای از اعضای متمایز (جدا از هم) میگویند که یک ویژگی مشترک دارند و این ویژگی را میتوان به راحتی توصیف و تعریف کرد.
مجموعه تهی چیست؟
مجموعههای تهی برای سادهسازی محاسبات استفاده میشوند و اغلب هنگام طبقهبندی موارد خارج از دسترس یا مواردی که نادر هستند به کار میروند. در اینجا چند مثال را بیان میکنیم که در آن میتوان از یک مجموعه تهی برای طبقهبندی اعضای خارج از دسترس یا نشدنی استفاده کرد. به عنوان مثال، یک ماه با 33 روز، یک هفته با دو سهشنبه، یا یک گربه با پنج پا. کمی پیشتر میرویم و تعریف مجموعه تهی را بیان میکنیم.

یک مجموعه به عنوان یک مجموعه خالی یا یک «مجموعه تهی» (Null Set یا Empty Set) تعریف میشود اگر هیچ عضوی نداشته باشد. در تئوری مجموعهها، ممکن است از یک مجموعه تهی برای دستهبندی یک عدد طبیعی بین 6 و 7 استفاده شود. از آنجا که این مثال هیچ پاسخ مشخصی ندارد، میتوان آن را با استفاده از یک مجموعه خالی یا یک مجموعه تهی نشان داد.
مثالهای زیر را در نظر بگیرید که در آن باید تعیین کنیم که مجموعههای داده شده مجموعه تهی هستند یا خیر.
الف) {x کوچکتر از ۱۶ و بزرگتر از ۱۴ و x یک عدد اول است : x} = X: مجموعه اعداد اول را A در نظر میگیریم. بنابراین، A = {2, 3, 5, 7, 11, 13, 17, …}. از آنجا که هیچ عدد اولی بین 14 و 16 وجود ندارد، میتوانیم نتیجه بگیریم که X یک مجموعه تهی است.
ب) تعداد وانتهایی با 12 در: در زندگی واقعی، مگر اینکه شرایطی وجود داشته باشد که یک شرکت تولیدکننده مدل خاصی را تولید کند، یافتن وانتی با 12 در غیرممکن است. بنابراین مجموعه شامل وانتهایی با ۱۲ در یک مجموعه تهی است.
با توجه به اینکه مجموعههای تهی یکی از دروس ریاضی نهم نیز به شمار میآید، برای آشنایی بیشتر با این درس، مطالعه مطلب زیر پیشنهاد میشود.
علامت محموعه تهی چیست ؟
یک مجموعه تهی با علامت { } نشان داده میشود که هیچ عضوی در آن وجود ندارد. همچنین از نماد "∅" نیز برای نشان دادن مجموعه تهی استفاده میشود.

عدد اصلی یا تعداد اعضای مجموعه تهی
مجموعههای تهی در نظریه مجموعهها مجموعههای منحصربهفردی در نظر گرفته میشوند و بنابراین، دارای یک کاردینالیته (عدد اصلی) منحصر به فرد هستند.
عدد اصلی به عنوان اندازه مجموعه یا تعداد کل اعضای موجود در یک مجموعه تعریف میشود. از آنجا که مجموعه تهی هیچ عضوی ندارد، میتوان گفت که عدد اصلی آن صفر است.
چگونه یک مجموعه تهی را نشان میدهیم؟
در تئوری مجموعهها، مجموعههای تهی را با استفاده از قلابهای خالیِ { } نشان داده میشوند. با این حال، از آنجا که مجموعههای تهی از انواع منحصر به فرد مجموعه هستند، میتوان آنها با استفاده از کاراکتر ویژه ∅ نیز نمایش داد. مثالی از یک مجموعه تهی A شامل مضربهای 5 بین 6 و 8 در نظر بگیرید. از آنجا که هیچ مضربی از 5 بین 6 و 8 وجود ندارد، بنابراین مجموعه داده شده یک مجموعه تهی است. مجموعه {x کوچکتر از ۸ و بزرگتر از ۶ و اول است : x} = A. نماد این مجموعه تهی این است: {} = A. برای نمایش این مجموعه تهی میتوانیم از نماد ویژه ∅=A نیز استفاده کنیم.
تفاوت بین مجموعه صفر و مجموعه تهی چیست؟
اغلب مفاهیم مجموعههای صفر و مجموعههای تهی یکسان در نظر گرفته میشوند و حتی اصطلاحات (مجموعه صفر و مجموعه تهی) به جای یکدیگر استفاده میشوند. با داشتن درک روشن از این دو مجموعه میتوان از این تصور غلط جلوگیری کرد.

مجموعه صفر مجموعهای است که تنها عضو آن عدد صفر (0) است و آن را با {0} نشان میدهیم. دقت کنید که به 0 مانند هر عدد دیگری نگاه میکنیم و در اینجا، بحث ارزش عدد مطرح نیست. اما مجموعه تهی مجموعهای است که هیچ عضوی ندارد و با { } نمایش داده میشود. دقت کنید که مجموعه {Ø} تهی نیست، زیرا دارای عضو Ø است.
مجموعه تهی چند زیرمجموعه دارد؟
مجموعه تهی تنها یک زیرمجموعه دارد و آن هم خودش است.
با توجه به اینکه تعداد اعضای مجموعه تهی ۰ است، از فرمول 1=20 نیز میتوان تعداد اعضا را بهدست آورد که همان ۱ است.
نمودار ون مجموعه تهی
نمودارهای ون موثرترین ابزار برای نمایش روابط بین مجموعهها، به ویژه مجموعههای متناهی هستند. میتوانیم یک مجموعه تهی را با نمودار ون نشان دهیم. بخش آبی نمودار ون تصویر زیر مجموعه تهی را نشان میدهد. مجموعه X = {1, 3, 5} و مجموعه Y = {2, 4, 6} را در نمودار ون مشاهده میکنید.
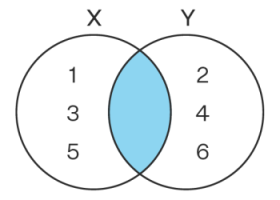
از نمودار ون که در بالا ارائه شده است میتوانیم ببینیم که هیچ عضو مشترکی بین دو مجموعه X و Y وجود ندارد. از این رو میتوان نتیجه گرفت که اشتراک بین این دو مجموعه تهی است. بنابراین، ∅ = X ∩ Y.
مجموعه تهی چه ویژگیهایی دارد؟
معمولاً مجموعه تهی نقش مهمی در طبقهبندی اشیایی دارد که منحصر به فرد و عجیب هستند. علاوه بر آسانتر کردن طبقهبندی، از مجموعههای تهی برای سادهسازی محاسبات استفاده میشود. در ادامه، برخی از ویژگیهای مهم مجموعههای تهی آورده شده است:
مجموعه تهی زیرمجموعه هر مجموعهای است: یک مجموعه تعی را می توان به عنوان زیرمجموعه هر مجموعه ای در نظر گرفت. برای هر مجموعه متناهی یا نامتناهی X، اگر همه زیرمجموعههای ممکن مجموعه X را حذف کنیم، همیشه میتوانیم یک مجموعه تهی را در آن قرار دهیم.
مثلا، یک مجموعه نامتناهی X = {1, 3, 5} را در نظر بگیرید. تمام زیرمجموعههای ممکن این مجموعه X را میتوان به صورت زیر نوشت:
∅ = X و X = {1} و X = {3} و X = {5} و X = {1, 3} و X = {3, 5} و X = {1, 5}
همانطور که میبینید، مجموعه تهی نیز به همراه زیرمجموعههای دیگر آورده شده است.
اجتماع مجموعه تهی با هر مجموعه دیگری برابر با آن مجموعه دیگر است: عملیات اجتماع بین هر مجموعه و مجموعه تهی همیشه به آن مجموعه منجر میشود. برای هر مجموعه متناهی یا نامتناهی X، اتحاد این مجموعه X با یک مجموعه تهی X U ∅ = X است. از آنجا که یک مجموعه تهی حاوی هیچ عوضوی از خود نیست، اجتماع بین یک مجموعه تهی و هر مجموعه X همان X را ایجاد میکند.
مثلاً، مجموعه X = {1, 2, 3, 4} را در نظر بگیرید. اجتماع مجموعه داده شده X با یک مجموعه تهی را میتوان به صورت X U ∅ = {1, 2, 3, 4} U {} نشان داد. بنابراین، A U ∅ = {1, 2, 3, 4}.
اشتراک مجموعه تهی با هر مجموعه دیگری برابر با مجموعه تهی است: عمل اشتراک بین هر مجموعه و مجموعه تهی همیشه به خود مجموعه تهی منجر میشود. برای هر مجموعه متناهی یا نامتناهی X، اشتراک مجموعه X با یک مجموعه تهی ∅ = X ∩ ∅ است. از آنجا که یک مجموعه تهی حاوی هیچ عضوی نیست، هیچ عنصر مشترکی بین هر مجموعه غیرتهی و تهی وجود نخواهد داشت.
برای مثال، مجموعه X = {2, 4, 6} را در نظر بگیرید. اشتراک مجموعه داده شده X با یک مجموعه تهی را میتوان به صورت ∅ = X ∩ ∅ نشان داد.
آزمون مجموعه تهی
۱. کدام گزینه تعریف درست مجموعه تهی و دو نماد متداول نمایش آن را بیان میکند؟
مجموعه تهی مجموعهای با یک عضو است و با نماد {0} و ∅ نمایش مییابد.
مجموعه تهی مجموعهای بدون عضو است و با نمادهای ∅ و {} نمایش داده میشود.
مجموعه تهی مجموعهای با تنها عضو صفر است و با نماد {0} و {} نمایش میگردد.
مجموعه تهی مجموعهای با اعضای نامشخص است و با نماد {x} و {} نشان داده میشود.
تعریف درست این است که «مجموعه تهی مجموعهای است که هیچ عضوی ندارد و با نمادهای ∅ (فی) و {} نمایش داده میشود». این تعریف، هم به خالی بودن مجموعه اشاره دارد و هم دقیقا دو نماد متداول را معرفی میکند. عبارت «مجموعهای با یک عضو» اشتباه است، زیرا چنین مجموعهای تهی محسوب نمیشود. نمونههایی چون {0} یا {x} نیز به مجموعههایی با اعضا مربوط هستند، نه مجموعه تهی. تنها عبارت مرتبط با مجموعه بدون هیچ عضو و دو نماد ∅ و {}، تعریف درست را ارائه داده است.
۲. در ریاضیات، تفاوت اصلی بین مجموعه صفر {0} و مجموعه تهی {} در چیست و هرکدام چه ویژگی خاصی دارند؟
مجموعه تهی {} هیچ عضوی ندارد، اما مجموعه صفر {0} یک عضو دارد که صفر است.
مجموعه تهی {} همیشه بزرگتر از مجموعه صفر {0} است.
مجموعه صفر {0} همان مجموعه تهی {} است و تفاوتی ندارند.
هر دو مجموعه تهی {} و مجموعه صفر {0} شامل هیچ عضوی نیستند.
در مجموعه تهی {} هیچ عضوی وجود ندارد و کاملا خالی است، در حالی که مجموعه صفر {0} دارای یک عضو است که همان عدد صفر میباشد.
۳. اگر مجموعه X و مجموعه Y هیچ عضو مشترکی نداشته باشند، اشتراک این دو مجموعه طبق نمودار ون کدام است؟
اشتراک X و Y همان مجموعه تهی (∅ یا {}) خواهد بود.
اشتراک X و Y برابر با مجموعهای است که عضو ندارد اما با {0} نمایش داده میشود.
اشتراک X و Y شامل هر دو مجموعه X و Y میشود.
اشتراک X و Y برابر با مجموعهای است که فقط شامل صفر باشد.
وقتی هیچ عضو مشترکی میان X و Y وجود نداشته باشد، اشتراک آنها با تعریف مجموعه تهی مطابقت دارد که هیچ عضوی ندارد و معمولا با ∅ یا {} نمایش داده میشود.













تشکر بابت بلاگ درسیتون .
اینجا یه اشکال ریزی هست کلمه اجتماع باید به اشتراک تبدیل شه تا درست باشه .
“برای مثال، مجموعه X = {2, 4, 6} را در نظر بگیرید. اجتماع مجموعه داده شده X با یک مجموعه تهی را میتوان به صورت ∅ = X ∩ ∅ نشان داد”
تهی عضو همه مجموعه هاست؟
با سلام و وقت بخیر؛
متن اصلاح شد. ممنون از دقت نظر شما.
از همراهیتان با مجله فرادرس سپاسگزاریم.
اگر ۲ مجموعه تهی رو از هم کم کنیم بازم تهی به دست میاد؟
سلام.
بله، جواب یک مجموعه تهی است.
موفق باشید.