فرمول محیط متوازی الاضلاع چیست؟ – معرفی انواع فرمول ها + حل مثال
فرمول محیط متوازی الاضلاع برابر «عرض × 2 + طول × 2» یا «P=2a+2b» است. فرمولهای دیگری نیز برای محاسبه محیط متوازیالاضلاع وجود دارند که بر اساس اندازه ارتفاع و قطر نوشته میشوند. در این آموزش، به معرفی فرمول محیط متوازی الاضلاع و روشهای مختلف محاسبه محیط به همراه حل چند مثال میپردازیم.

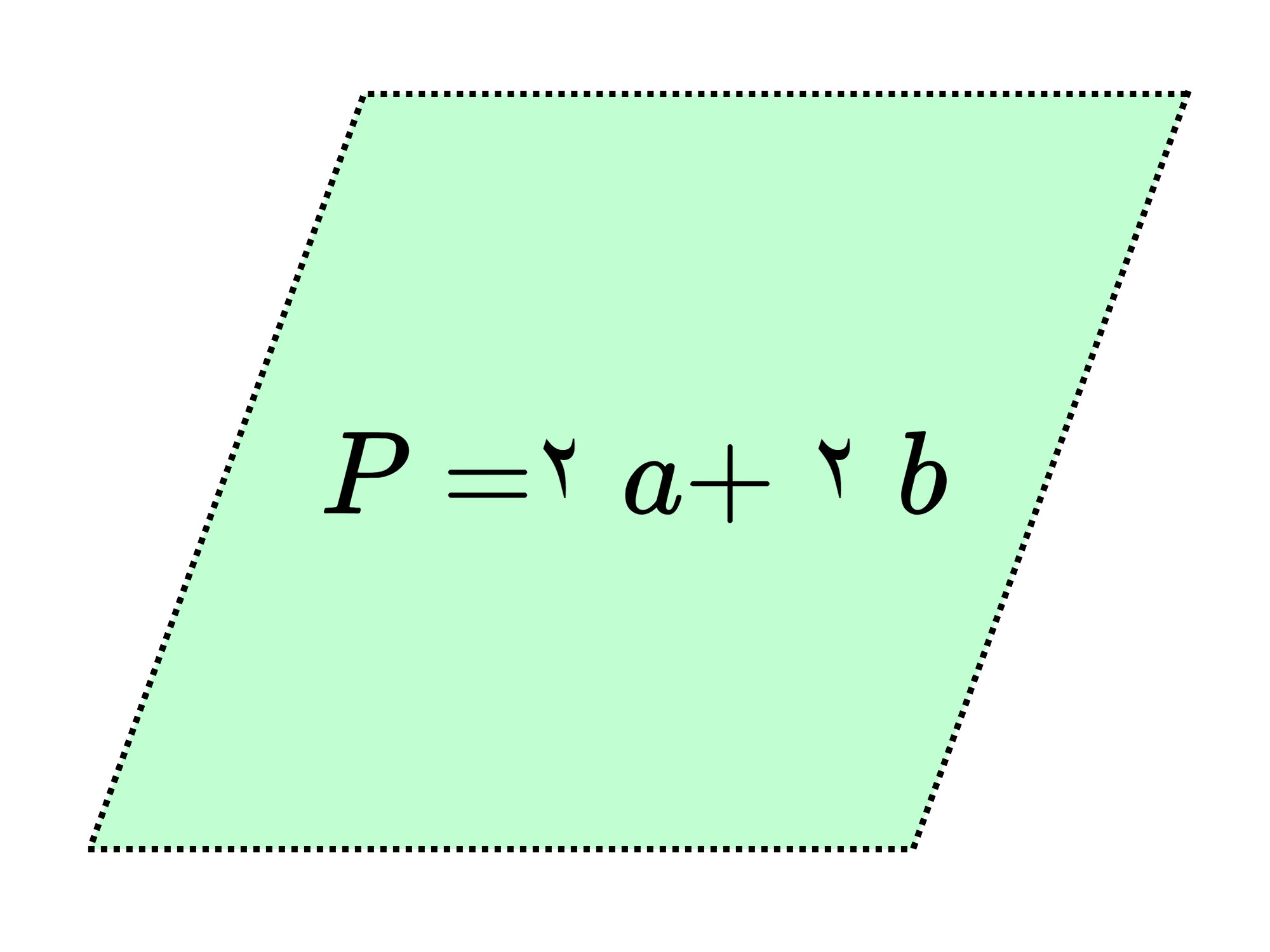
محیط متوازی الاضلاع چیست؟
به اندازه دور متوازی الاضلاع، محیط آن میگویند. به عبارت دیگر، محیط متوازی الاضلاع، مسافت روی ضلعهای آن است.

محیط متوازی الاضلاع چگونه تعیین میشود؟
محیط متوازی الاضلاع با محاسبه حاصلجمع ضلعهای آن تعیین میشود. متوازی الاضلاع، چهار ضلع دارد. بنابراین، محیط این شکل هندسی از رابطه زیر به دست میآید:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع
مثال 1: محاسبه اندازه دور متوازی الاضلاع
اندازه هر یک از ضلعهای متوازیالاضلاع زیر، در کنار آن نمایش داده شده است. محیط متوازیالاضلاع را حساب کنید.
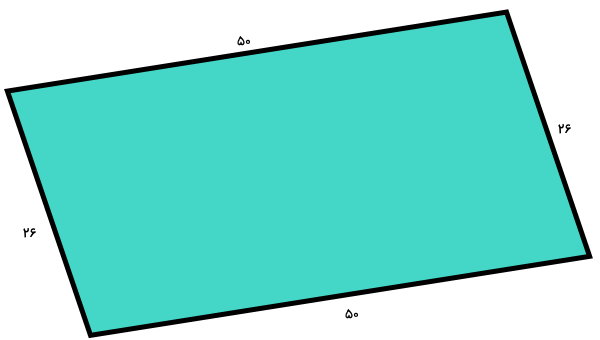
اندازه محیط متوازیالاضلاع بالا، از جمع چهار ضلع آن به دست میآید:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط متوازی الاضلاع
۲۶ + ۵۰ + ۲۶ + ۵۰ = محیط متوازی الاضلاع
۱۵۲ = محیط متوازی الاضلاع
در نتیجه، محیط متوازیالاضلاع برابر 152 واحد طول است.
فرمول محیط متوازی الاضلاع چیست؟
در متوازی الاضلاع، ضلعهای مقابل با یکدیگر موازی و هماندازه هستند. با توجه به این نکته، فرمول محیط متوازی الاضلاع به صورت زیر نوشته میشود:
(ضلع دوم × 2) + (ضلع اول × 2) = محیط متوازی الاضلاع
به ضلعهای بزرگ متوازیالاضلاع، «طول» و به ضلعهای کوچک آن، «عرض» میگویند. فرمول زیر، یکی دیگر از روشهای نوشتن فرمول محیط متوازی الاضلاع است:
(عرض + طول) × 2 = محیط متوازی الاضلاع
به طور کلی میتوانیم فرمول محیط متوازی الاضلاع را به صورت زیر بنویسیم:
(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع
مثال 2: محاسبه محیط متوازی الاضلاع با فرمول
اندازه دو ضلع مجاور در یک متوازیالاضلع برابر 21 و 24 سانتیمتر است. محیط متوازیالاضلاع را به دست بیاورید.
برای حل این مسئله، فرمول محیط متوازیالاضلاع را مینویسیم و اندازههای معلوم را درون آن قرار میدهیم:
(عرض × 2) + (طول × 2) = محیط متوازیالاضلاع
(۲۴ × 2) + (۲۱ × 2) = محیط متوازیالاضلاع
(۴۸) + (۴۲) = محیط متوازیالاضلاع
۹۰ = محیط متوازیالاضلاع
در نتیجه، محیط متوازیالاضلاع برابر ۹۰ سانتیمتر است.
محیط متوازی الاضلاع به صورت جبری
متوازیالاضلاع زیر را در نظر بگیرید. اندازه ضلعهای این متوازیالاضلاع با حروف انگلیسی نمایش داده شده است.
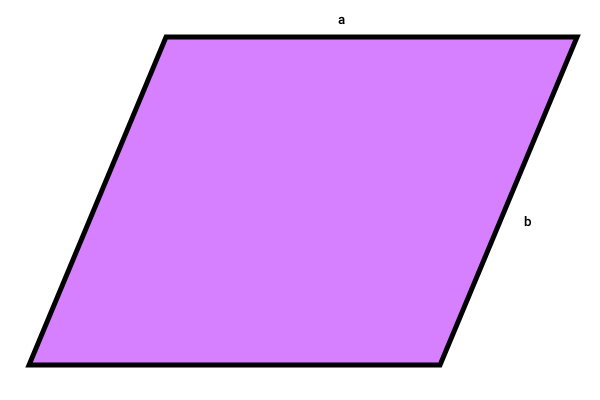
محیط متوازیالاضلاع بالا از فرمول زیر به دست میآید:
(عرض × 2) + (طول × 2) = محیط متوازی الاضلاع
2a + ۲b = محیط متوازی الاضلاع
یا
(جمع دو ضلع مجاور) × 2 = محیط متوازی الاضلاع
(a + b) × 2 = محیط متوازی الاضلاع
اگر به جای عبارت «محیط متوازی الاضلاع»، از حرف P (ابتدای کلمه Perimeter به معنای محیط) را قرار دهیم، فرمولهای بالا به شکل زیر در میآیند:
فرمولهای بالا، محیط متوازی الاضلاع را با استفاده از حروف، اعداد و عملهای ریاضی نمایش میدهند. این فرمولها، عبارتهای جبری محاسبه محیط متوازیالاضلاع هستند.
مثال 3: محاسبه محیط متوازی الاضلاع به صورت جبری
تصویر زیر، یک مستطیل به طول 15/3 و عرض 9/5 را نمایش میدهد. محیط شکل را به صورت جبری محاسبه کنید.
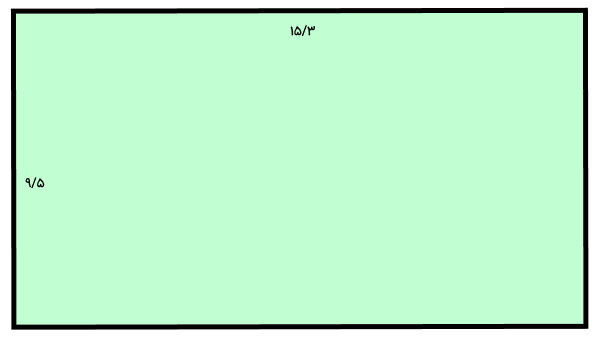
مستطیل، متوازیالاضلاعی است که تمام ضلعهای آن بر هم عمود هستند. از اینرو، برای محاسبه محیط آن میتوانیم از فرمول جبری محیط متوازیالاضلاع استفاده کنیم:
- P: محیط مستطیل
- a: طول مستطیل برابر 15/3
- b: عرض مستطیل برابر 9/5
در نتیجه، محیط متوازی الاضلاع برابر ۴۹/۶ واحد طول است.
انواع فرمول های محیط متوازی الاضلاع
فرمول اصلی محیط متوازی الاضلاع، همان فرمولی است که در بخشهای قبلی معرفی کردیم. با این وجود، اگر هر دو اندازه ضلعهای مجاور معلوم نباشند، امکان محاسبه محیط با استفاده از اندازه قطرها، ارتفاع و زاویه نیز وجود دارد.
جدول زیر، فرمول های محیط متوازی الاضلاع را بر اساس اندازههای معلوم نمایش میدهد.
| اندازه معلوم متوازی الاضلاع | فرمول محیط |
| دو ضلع مجاور | |
| دو قطر و یک ضلع | |
| قاعده (یک ضلع)، ارتفاع نظیر و یک زاویه | |
| قاعده (یک ضلع)، ارتفاع نظیر و مساحت |
مثال 4: محاسبه محیط متوازی الاضلاع با قطر
اندازه قطرهای یک متوازیالاضلاع برابر 10 و 12 متر است. اگر اندازه یکی ضلعهای آن برابر 8 متر باشد، محیط آن چقدر خواهد بود؟
با توجه اندازههای معلوم، محیط متوازیالاضلاع با استفاده از فرمول زیر قابل محاسبه است:
- P: محیط متوازیالاضلاع
- a: یکی از ضلعها برابر 8 متر
- x: یکی از قطرها برابر 10 متر
- y: قطر دیگر برابر 12 متر
در نتیجه، محیط متوازیالاضلاع برابر ۳۱/۲۳ متر است.
مثال 5: محاسبه محیط متوازی الاضلاع با ارتفاع
متوازیالاضلاعی ضلع 15 و ارتفاع نظیر 20 را در نظر بگیرید. با فرض وجود زاویه 30 درجه بین ضلعهای مجاور، محیط متوازیالاضلاع را حساب کنید.
اگر ارتفاع، ضلع و زاویه بین اضلاع یک متوازیالاضلاع را داشته باشیم، محیط آن از رابطه زیر به دست میآید:
- P: محیط متوازیالاضلاع
- a: یکی از ضلعها برابر 15
- h: ارتفاع نظیر ضلع a
- θ: زاویه بین اضلاع مجاور برابر 30 درجه
سینوس زاویه ۳۰ درجه برابر ۰/۵ است:
در نتیجه، محیط متوازیالاضلاع برابر ۱۱۰ واحد طول است.
سوالات متداول در رابطه با فرمول محیط متوازی الاضلاع
در این بخش، به برخی از سوالات متداول در رابطه با فرمول محیط متوازیالاضلاع به طور خلاصه پاسخ میدهیم.
محیط متوازیالاضلاع چیست؟
محیط متوازیالاضلاع، جمع ضلعهای آن است.
محیط متوازیالاضلاع چگونه بدست میآید؟
محیط متوازیالاضلاع از جمع دو ضلع مجاور ضربدر دو به دست میآید.
فرمول محیط متوازیالاضلاع چیست؟
(ضلع دوم × 2) + (ضلع اول × 2)، فرمول اصلی محیط متوازیالاضلاع است.
عبارت جبری محیط متوازیالاضلاع چیست؟
عبارت جبری فرمول محیط متوازیالاضلاع، P=2a+۲b است.
آیا امکان محاسبه محیط متوازیالاضلاع با قطر وجود دارد؟
بله. در صورت مشخص بودن اندازه دو قطر و یک ضلع متوازیالاضلاع، میتوان محیط آن را حساب کرد.
آیا امکان محاسبه محیط متوازیالاضلاع با ارتفاع وجود دارد؟
بله. اگر اندازه یک زاویه، یک ضلع و ارتفاع نظیر آن ضلع را داشته باشیم، میتوانیم محیط متوازیالاضلاع را به دست بیاوریم.
آزمون محیط متوازی الاضلاع
۱. فرمول جبری محیط متوازیالاضلاع با استفاده از نمادهای a و b چیست و این نمادها به چه مفهومی اشاره دارند؟
فرمول P=a×b است، که a محیط و b قطر متوازیالاضلاع هستند.
فرمول P=2a+2b است، که a طول و b عرض متوازیالاضلاع هستند.
فرمول P=ab+2 است، که a مساحت و b ارتفاع شکل هستند.
فرمول P=a+b است، که a طول و b زاویه داخلی متوازیالاضلاع هستند.
فرمول اصلی محیط متوازیالاضلاع با نمادهای a و b به صورت P=2a+2b نوشته میشود. در این فرمول منظور از a طول و منظور از b عرض متوازیالاضلاع است.
۲. در چه حالتی لازم است هنگام محاسبه محیط متوازیالاضلاع به جای فرمول P=2a+2b از فرمولهایی بر پایه قطر، ارتفاع یا زاویه استفاده کنیم؟
هنگامی که ابعاد با اعداد اعشاری بیان شود.
وقتی فقط اندازه قطر یا ارتفاع یا زاویه در اختیار باشد.
وقتی هر دو ضلع مجاور و برابر مشخص باشند..
زمانی که تنها مساحت شکل معلوم باشد.
در صورتی باید از فرمولهایی مثل استفاده از قطر، ارتفاع یا زاویه برای محیط متوازیالاضلاع بهره برد که اطلاعاتی درباره ضلعهای مجاور وجود نداشته باشد و فقط اندازههایی همچون یک یا هر دو قطر، ارتفاع شکل یا زاویه بین اضلاع معلوم باشد. راه مستقیم با فرمول P=2a+2b زمانی قابل استفاده است که طول اضلاع مجاور داده شدهاند. اگر فقط اندازه قطر یا ارتفاع یا زاویه موجود باشد، فرمولهای ویژه وارد عمل میشوند.
۳. اگر طول یکی از قطرهای متوازیالاضلاع و اندازه یک ضلع را داشته باشیم و اطلاعاتی از سایر اضلاع یا ارتفاع نداشته باشیم، بهترین روش برای محاسبه محیط چیست؟
کاربرد فرمول محیط بر پایه ارتفاع و زاویه
بهکارگیری فرمول محیط با استفاده از ضلع و قطر
محاسبه محیط به روش جبری با نمادهای a و b
استفاده از جمع تمام ضلعها بدون نیاز به قطر
در حالتی که فقط طول یک قطر و یک ضلع متوازیالاضلاع داده شده باشد، فرمول اختصاصی محیط که هم ضلع و هم قطر را بهطور همزمان در محاسبه شرکت میدهد مناسبترین گزینه است. روش «بهکارگیری فرمول محیط با استفاده از ضلع و قطر» دقیقا همین حالت را پوشش میدهد و برای شرایطی که هیچ اطلاعی از ارتفاع یا اضلاع دیگر نداریم کارآمد است. گزینههایی مثل جمع همه اضلاع یا فرمول جبری با a و b نیازمند دانستن مقادیر هر دو ضلع هستند. همچنین، فرمول مرتبط با ارتفاع و زاویه زمانی کاربرد دارد که این دادهها مشخص باشند؛ اما در این حالت فقط قطر و یک ضلع معلوم است.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- متوازی الاضلاع چیست ؟ — تعریف و مفاهیم به زبان ساده
- محیط متوازی الاضلاع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط متوازی الاضلاع چیست ؟ — معرفی انواع فرمول ها + حل مثال(همین مطلب)
- مساحت متوازی الاضلاع چطور محاسبه می شود؟ – جامع + مثال، تمرین و فیلم رایگان
- محاسبه قطر متوازی الاضلاع — فرمول های محاسبه + حل تمرین و مثال
- محیط متوازی الاضلاع به صورت جبری — فرمول های ریاضی + حل مثال
- فرمول مساحت متوازی الاضلاع چیست ؟ — تمامی فرمول ها + حل تمرین و مثال
- مساحت متوازی الاضلاع به صورت جبری — انواع فرمول ها + حل مثال
- نمونه سوال مساحت متوازی الاضلاع با جواب — حل تمرین های متنوع
- مساحت متوازی الاضلاع با قطر چگونه بدست می آید ؟ + حل مثال
- مساحت متوازی الاضلاع با سینوس — به زبان ساده + حل مثال












