فرم دیفرانسیلی معادلات ماکسول — به زبان ساده

در مقاله «معادلات ماکسول (Maxwell’s Equations) — به زبان ساده [لینک مقاله]» به طور کامل با معادلات ماکسول و توضیحات مربوط به هر معادله، آشنا شدید. در این مقاله قصد داریم تا با زبانی ساده، فرم دیفرانسیلی معادلات ماکسول را از روی معادلات انتگرالی آن‌ها به دست آوریم. با ما در ادامه این مطلب همراه باشید.

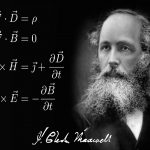
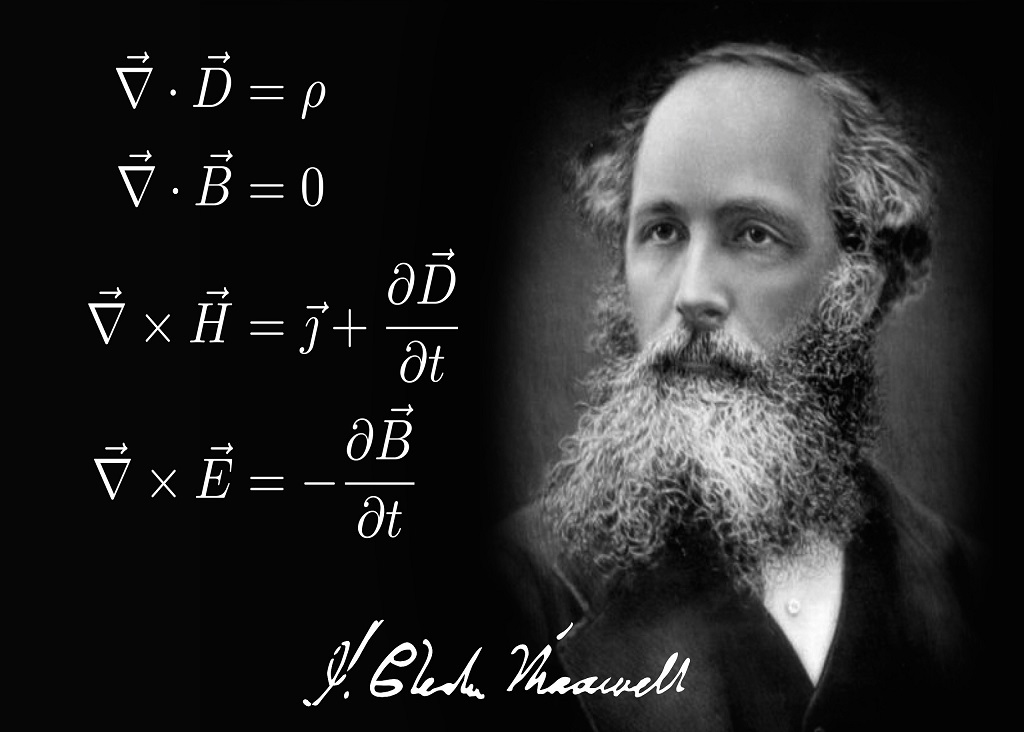
دانشجویان در طی مطالعه فیزیک الکتریسیته و مغناطیس رفته رفته با معادلاتی غالباً انتگرالی آشنا می‌شوند که هر یک به تنهایی قادر است پاسخ بخشی از سوالات مطرح شده در زمینه الکتریسیته یا مغناطیس را بدهد. می‌توان گفت این معادلات حاصل پژوهش‌های سه دانشمند بزرگ به نام‌های گاوس (Carl Friedrich Gauss)، آمپر (Andre Marie Ampere) و فارادی (Michael Faraday) است که نهایتاً توسط دانشمند انگلیسی جیمز کلارک ماکسول (James Clerk Maxwell) تعمیم یافتند و در ۴ معادله جمع‌بندی شدند. این ۴ معادله که به معادلات ماکسول موسوم هستند، جامعیت داشته و تمامی مسائل حوزه الکترومغناطیس را پوشش می‌دهند. البته ناگفته نماند که وارد کردن این معادلات به حوزه‌های نسبیتی و کوانتومی نیز خود نیازمند تغییراتی است.

فیلم آموزش اپتیک کوانتومی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

فرم انتگرالی معادلات ماکسول از این حیث که دو مفهوم مهم شار الکتریکی و شار مغناطیسی را در بردارد، جهت درک فیزیک الکتریسیته و مغناطیس بسیار حائز اهمیت هستند. با این حال در اکثر علوم مهندسی و مباحث فیزیک پیشرفته از فرم دیفرانسیلی معادلات ماکسول استفاده می‌کنند.

مروری بر مبانی الکترومغناطیس

قبل از به دست آوردن فرم دیفرانسیلی معادلات ماکسول از فرم انتگرالی آن‌ها، بهتر است که جهت یادآوری، مروری بر آموخته‌های قبلی از مجله فرادرس داشته باشیم.

فیلم آموزش الکترومغناطیس مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

فرم انتگرالی معادلات ماکسول به صورت زیر است:

$$\large \begin{equation} \oint_{S} D \cdot d S = \int_{V} \rho d V \end{equation}$$
(1)

$$\large \begin{equation} \oint_{S} B \cdot d S = 0 \end{equation}$$
(2)

$$\large \begin{equation} \oint_{C} E \cdot d l = -\frac{d}{d t} \int_{S} B \cdot d S \end{equation}$$
(3)

$$\large \begin{equation} \oint_{C} H \cdot d l = \int_{S} J \cdot d S+\frac{d}{d t} \int_{S} D \cdot d S \end{equation}$$
(4)

در معادلات فوق، $$\rho$$ چگالی بار الکتریکی، $$J$$ چگالی جریان الکتریکی، $$E$$ شدت میدان الکتریکی، $$H$$ شدت میدان مغناطیسی، $$D$$ جابه‌جایی الکتریکی (چگالی قطبش) و $$B$$ چگالی شار مغناطیسی هستند.

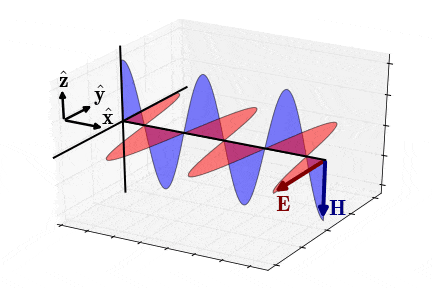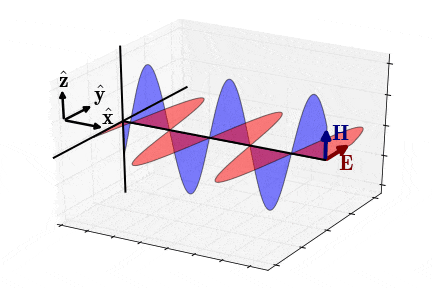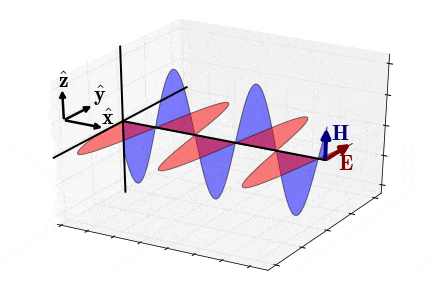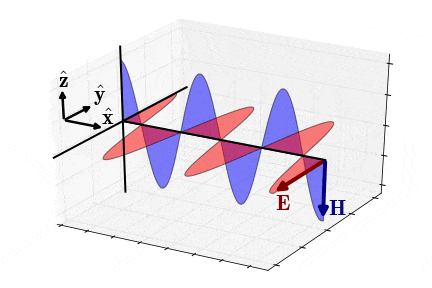
برای دو پارامتر $$D$$ و $$B$$ نیز داریم:

$$\large \begin{equation} D = \varepsilon_{0} E + P = \left(1+\chi_{e}\right) \varepsilon_{0} E = \varepsilon E \end{equation}$$
(5)

$$\large \begin{equation} B = \mu_{0}(H + M) = \left(1+\chi_{m}\right) \mu_{0} H = \mu H \end{equation}$$
(6)

$$\large P = \chi_{e} \varepsilon_{0} E$$
(7)

$$\large M = \chi_{m} H$$
(8)

در معادلات فوق، $$\varepsilon$$ ضریب نفوذپذیری (گذردهی) الکتریکی محیط، $$\varepsilon_{0}$$ ضریب نفوذپذیری (گذردهی) الکتریکی خلأ، $$\mu$$ ضریب نفوذپذیری (تراوایی) مغناطیسی محیط، $$\mu_{0}$$ ضریب نفوذپذیری (تراوایی) مغناطیسی خلأ، $$\chi_{e}$$ پذیرفتاری الکتریکی محیط و $$\chi_{m}$$ پذیرفتاری مغناطیسی محیط است.

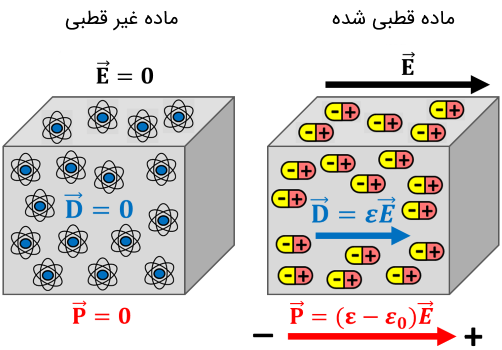
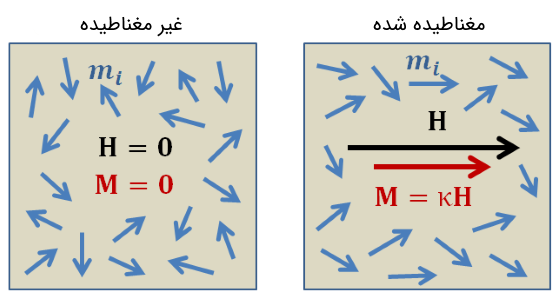
در الکترومغناطیس، پذیرفتاری یا حساسیت الکتریکی (Electric susceptibility) که با نماد $$\chi_{e}$$ نمایش داده می‌شود، یک ثابت تناسب بدون واحد است که درجه قطبیدگی ماده دی‌الکتریک را در پاسخ به میدان الکتریکی تعیین می‌کند. مطابق با رابطه (۷) ، هر چه اندازه $$\chi_{e}$$ بزرگ‌تر باشد، ماده راحت‌تر در قبال میدان الکتریکی قطبیده می‌شود که این به معنی کاهش میدان خارجی در جسم است. در نتیجه پذیرفتاری الکتریکی بر گذردهی الکتریکی ماده تاثیر گذاشته که به تبع متغیرهای دیگری نظیر ظرفیت خازنی و سرعت نور (موج) در محیط دچار تغییر می‌شوند (به دلیل تغییر ضریب شکست). لازم به ذکر است که $$\chi_{e}$$ در کل ماهیتی تانسوری داشته و یک تانسور مرتبه دو با ۹ مولفه است. $$P$$ نیز بردار قطبش الکتریکی است (شکل ۴).

مشابه با تعریف پذیرفتاری الکتریکی، پذیرفتاری مغناطیسی (Magnetic susceptibility) که آن را با نماد $$\chi_{m}$$ نشان می‌دهند، میزان قابلیت مغناطیده شدن ماده را مشخص می‌کند. بر اساس پارامتر $$\chi_{m}$$ خواص مغناطیسی، نظیر فرومغناطیس، دیامغناطیس و یا پارامغناطیس بودن ماده تعیین می‌شود. $$M$$ (مغناطش - Magnetization) نیز برداری‌ است که چگالی گشتاورهای مغناطیسی (دائم یا القایی) را در یک ماده مغناطیسی نشان می‌دهد. منشأ گشتاورهای مغناطیسی مولد $$M$$ و $$\chi_{m}$$، جریان الکتریکی ناشی از حرکت الکترون‌های اتم، اسپین هسته و ساختار الکترونی اتم‌ها است.

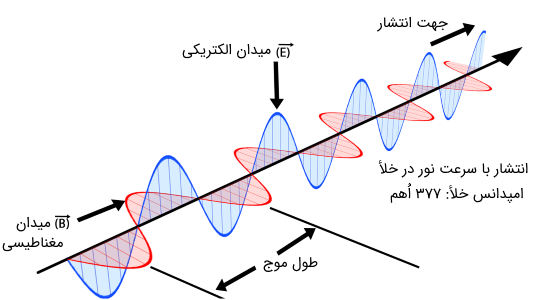
سرعت امواج الکترومغناطیسی که توسط ۴ معادله ماکسول توصیف می‌شوند، در خلأ برابر با سرعت نور است. این سرعت در محیط‌های مادی به دلیل وجود پارامتر $$n$$ (ضریب شکست) که خود در حالت کلی تابعی از فرکانس (طول موج) است، متفاوت خواهد بود.

$$\large c = \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}}\cong3\times10^{8}\ (\frac{m}{s})$$
(9)

همچنین برای امواج مذکور، امپدانس محیط که به امپدانس موج نیز موسوم است (مقاومتی که موج حین انتشار احساس می‌کند)، به صورت زیر محاسبه می‌شود:

$$\large \eta = \frac{E_{0}}{H_{0}}=\frac{\omega\mu}{k}=c\mu=\sqrt{\frac{\mu}{\epsilon}}$$
(10)

$$\large \eta=\frac{\eta_{0}}{n}$$
(11)

$$\large \eta_{0}=\sqrt{\frac{\mu_{0}}{\epsilon_{0}}}=120\pi=377 \ Ω$$
(12)

$$n$$ نیز ضریب شکست محیط بوده که به صورت زیر تعریف می‌شود.

$$\large n = \frac{c}{v} \Leftrightarrow n=\sqrt{\frac{\epsilon}{\epsilon_{0}}}$$
(13)

همچنین نیرویی که به یک ذره باردار متحرک $$q$$ از سمت یک میدان الکترومغناطیسی وارد می‌شود، به نیروی لورنتس (Lorentz force) موسوم بوده و به شکل زیر است. جمله اول نیروی ناشی از میدان الکتریکی و جمله دوم نیرو ناشی از میدان مغناطیسی است.

$$\large \overrightarrow{F} = q (\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B})$$
(14)

فرم دیفرانسیلی معادلات ماکسول

در این بخش در نظر داریم تا با زبانی ساده و توضیحاتی گویا، فرم دیفرانسیلی معادلات ماکسول (معادلات ۱ تا ۴) را به دست آوریم.

فیلم آموزش الکترومغناطیس مهندسی – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

فرم دیفرانسیلی قانون گاوس

اگر دقت کرده باشید، معادله (۱)، همان قانون گاوس در الکتریسیته بوده که فرم ساده‌تر آن به صورت زیر است:

$$\large \begin{equation} \oint_{S} E \cdot d S = \frac{Q}{\epsilon_{0}} \end{equation}$$
(15)

می‌دانیم که بار الکتریکی با چگالی بار (حجمی) به صورت $$Q = \rho V \Leftrightarrow Q = \int \rho dV$$ رابطه دارد. در نتیجه:

$$\large \begin{equation} \oint_{S} E \cdot d S = \int_{V} \frac{\rho}{\epsilon_{0}} d V \end{equation}$$
(16)

قدم بعدی، بازنویسی سمت چپ معادله فوق، با استفاده از قضیه دیورژانس (divergence theorem) است. قضیه مذکور برای یک میدان برداری نظیر $$F$$ به صورت زیر است:

$$\large \begin{equation} \oint_{S} F \cdot d S = \int_{V}(\nabla \cdot F) d V \end{equation}$$
(17)

پس با توجه به رابطه فوق، سمت چپ معادله (16) به صورت زیر در می‌آید:

$$\large \begin{equation} \int_{V}(\nabla \cdot E) d V=\int_{V} \frac{\rho}{\epsilon_{0}} d V \end{equation}$$
(18)

حال جمله سمت راست را به آن سمت تساوی می‌بریم. در نتیجه:

$$\large \begin{equation} \int_{V}(\nabla \cdot E) d V-\int_{V} \frac{\rho}{\varepsilon_{0}} d V = 0 \Rightarrow \int_{V}\left(\nabla \cdot E-\frac{\rho}{\varepsilon_{0}}\right) d V = 0 \end{equation}$$
(19)

از آنجایی که انتگرال یک عبارت صفر شده است، در نتیجه خود عبارت مذکور نیز برابر با صفر است. در نتیجه داریم:

$$\large \begin{equation} \nabla \cdot E - \frac{\rho}{\epsilon_{0}} = 0 \end{equation}$$

$$\large \Rightarrow \begin{equation} \nabla \cdot E = \frac{\rho}{\epsilon_{0}} \end{equation}$$
(20)

رابطه (20) که به فرم دیفرانسیلی قانون گاوس نیز معروف است، اولین معادله از فرم دیفرانسیلی معادلات ماکسول را تشکیل می‌دهد.

فرم دیفرانسیلی قانون گاوس در مغناطیس

قانون گاوس در مغناطیس به شکل انتگرالی زیر است:

$$\large \begin{equation} \oint_{S} B \cdot d S=0 \end{equation}$$
(21)

با استفاده از قضیه دیورژانس (معادله 17)، می‌توانیم معادله فوق را به صورت زیر بازنویسی کنیم:

$$\large \int_{V}(\triangledown.B)dV = 0$$
(22)

از آنجایی که انتگرال یک عبارت صفر شده است، در نتیجه خود عبارت نیز صفر است. در نتیجه:

$$\large \triangledown.B = 0$$
(23)

معادله (23) دومین معادله از معادلات چهارگانه ماکسول است که بیان می‌کند تک قطبی مغناطیسی نمی‌تواند وجود داشته باشد.

فرم دیفرانسیلی قانون فارادی

فرم انتگرالی قانون القا فارادی، به شکل زیر است:

$$\large \oint_{C} E.dl = \frac{\text{d}}{\text{d}t} \oint_{S} B.dS$$
(24)

فیلم آموزش اپتیک کوانتومی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

سمت راست معادله فوق، همان تغییرات زمانی شار مغناطیسی و سمت چپ معادله همان ولتاژ القایی است.

حال با استفاده از قضیه استوکس (Stokes' theorem) سمت چپ معادله (24) را بازنویسی می‌کنیم. قضیه استوکس برای میدان برداری نظیر $$F$$ به صورت زیر است.

$$\large \oint_{C} F.dl = \oint_{S} (\triangledown \times F).dS$$
(25)

با توجه به قضیه فوق برای سمت چپ معادله (24) داریم:

$$\large \oint_{S} (\triangledown \times E).dS = -\frac{\text{d}}{\text{d}t} \oint_{S} B.dS$$
(26)

حال جمله سمت راست را به سمت چپ برده و کل معادله را در قالب یک جمله می‌نویسیم. یعنی:

$$\large \int_{S} (\triangledown \times E).dS\ +\ \frac{\text{d}}{\text{d}d} \int_{S} B.dS\ = 0$$

$$\large \Rightarrow \int_{S} (\triangledown \times E\ +\ \frac{\partial B}{\partial t}).dS = 0$$
(27)

از آنجایی که حاصل انتگرال صفر است، در نتیجه خود عبارت داخل انتگرال نیز صفر است. در نتیجه داریم:

$$\large \triangledown \times E\ =\ - \frac{\partial B}{\partial t}$$
(28)

معادله فوق، معادله سوم از معادلات چهارگانه ماکسول است که به فرم دیفرانسیلی قانون القای فارادی نیز موسوم است.

فرم دیفرانسیلی قانون آمپر - ماکسول

ماکسول با اضافه کردن جمله جریان جابه‌جایی به قانون آمپر، آن را به شکل زیر تعمیم داد:

$$\large \oint_{C} B.dl = \mu_{0} \int_{S} J.dS + \mu_{0}\varepsilon_{0} \frac{\text{d}}{\text{d}t} \int_{S} E.dS$$
(29)

در معادله فوق $$\varepsilon_{0} \frac{\text{d}}{\text{d}t} \int_{S} E.dS$$ جریان جابه‌جایی است که با نماد $$I_{D}$$ نیز آن را نشان می‌دهند. جمله $$\int_{S} J.dS$$ نیز جریان رسانشی است. تفاوت این دو جریان را می‌توان در مثال خازن متصل به باتری دید. جریان الکتریکی رسانشی جریانی است که در سیم‌های مدار جاری است ($$I_{D} = 0$$) و جریان الکتریکی جابه‌جایی جریانی است که بین صفحات خازن وجود دارد ($$I_{J} = 0$$). جمع این دو جریان را نیز جریان کل ($$I_{J} + I_{D} = I$$) می‌گویند.

حال با استفاده از قضیه استوکس، سمت چپ معادله (29) را بازنویسی می‌کنیم.

$$\large \oint_{S} (\triangledown\times B).dS = \mu_{0} \int_{S} J.dS + \mu_{0}\varepsilon_{0} \frac{\text{d}}{\text{d}t} \int_{S} E.dS$$
(30)

مشابه به بخش‌های قبلی، همه جملات را در یک سمت تساوی نوشته و از آنجایی که جزء دیفرانسیلی انتگرال‌های همگی $$dS$$ است، می‌توانیم تمامی جملات را در قالب یک جمله به صورت زیر بنویسیم:

$$\large \int_{S} (\triangledown \times B\ -\ \mu_{0}J\ -\ \mu_{0}\varepsilon_{0}\frac{\partial E}{\partial t}).dS = 0$$
(31)

عبارت داخل انتگرال برابر با صفر است. در نتیجه:

$$\large \triangledown \times B\ =\ \mu_{0}J\ +\ \mu_{0}\varepsilon_{0}\frac{\partial E}{\partial t}$$
(32)

معادله فوق، معادله چهارم و نهایی از معادلات چهارگانه ماکسول است که به فرم دیفرانسیلی قانون آمپر - ماکسول نیز موسوم است. مطابق با مطالب گفته شده در فوق، با استفاده از دو قضیه ریاضی - فیزیک دیورژانس و استوکس توانستیم فرم دیفرانسیلی معادلات ماکسول را بدست آوریم.

دقت داشته باشید که با توجه به دو عبارت $$\large \begin{equation} D = \varepsilon E \end{equation}$$ و $$\large \begin{equation} B = \mu H \end{equation}$$ می‌توان معادلات فوق را برحسب $$D$$ و $$H$$ نیز بنویسیم.

جهت جمع‌بندی، فرم دیفرانسیلی معادلات ماکسول به صورت زیر است:

$$\large \triangledown.D=\rho$$

$$\large \triangledown.B=0$$

$$\large \triangledown \times E=-\frac{\partial B}{\partial t}$$

$$\large \triangledown \times H=\frac{\partial D}{\partial t}+J$$

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• آنتن و فرستنده -- به زبان ساده
• امواج رادیویی -- به زبان ساده
• مخابرات فیبر نوری -- به زبان ساده

^^