ضرب اعداد اعشاری – آموزش با مثال و به زبان ساده
ضرب یکی از چهار عمل اصلی در ریاضی است که به همراه جمع و تفریق و تقسیم عملگرهای پایه را تشکیل میدهند. در این بخش به ضرب اعداد اعشاری خواهیم پرداخت. حتما میدانید که ضرب اعداد صحیح برای سادهسازی جمع به کار رفته است همین موضوع را برای اعداد اعشاری نیز میتوان به کار برد. ابتدا به مفهوم ضرب اعداد اعشاری به صورت مساحت مستطیل نگاه میکنیم و بعد با استفاده از روشهای غیرهندسی ضرب دو عدد اعشاری را انجام میدهیم. البته میدانید که هر عدد اعشاری را میتوان به صورت یک کسر متعارفی درآورد. بنابراین یک روش برای ضرب اعداد اعشاری میتواند به شکلی باشد که ابتدا آنها را به صورت کسری نوشته، سپس در هم ضرب کنیم. این موضوع را در این متن هم به کار خواهیم برد.

بهتر است قبل از مطالعه این مطلب، با مجموعه اعداد صحیح و اعشاری آشنا شوید تا درک مناسبی از ضرب اعداد اعشاری داشته باشید. با خواندن اعداد صحیح چیست و چه اعدادی هستند ؟ — به زبان ساده و اعداد اعشاری — به زبان ساده از مجله فرادرس با این دسته از اعداد آشنا میشوید. همچنین مطالعه ضرب متقاطع یا طرفین و وسطین — به زبان ساده و اعداد گویا — به زبان ساده از مجله فرادرس نیز خالی از فایده نیست.
ضرب اعداد اعشاری
برای نمایش عملگر ضرب از نماد (×) استفاده میکنیم و در سمت چپ آن یک عدد و در سمت راست نیز عدد دوم را نشان میدهیم. البته مهم نیست که عدد سمت چپ بزرگتر از سمت راست باشد یا خیر. از طرفی میدانیم که عمل ضرب خاصیت جابجایی دارد. برای مثال عمل ضرب دو عدد ۲۰ در ۳۰ را به صورت زیر نشان میدهیم.
۲۰ × ۳۰ = ۳۰ × ۲۰
تساوی بالا، جابجایی در ضرب را نشان میدهد. به عددهایی که در هم ضرب میشوند، عاملهای ضرب و به حاصل آنها حاصلضرب میگوییم. در اینجا ۲۰ و ۳۰ عامل های ضرب هستند و حاصلضرب آنها برابر با ۶۰۰ است. از آنجایی که هر دو عدد ۲۰ و ۳۰، اعداد صحیح بودند، با اطلاعاتی که از ضرب به یاد داریم، به راحتی ضرب را انجام دادیم.

ولی اگر قرار باشد که دو عدد اعشاری را در هم ضرب کنیم، باید دقت بیشتری کرده و ضرب را انجام دهیم. در ادامه سه راه کار یا روش برای ضرب اعداد اعشاری معرفی میکنیم. شما میتوانید از هر کدام که برایتان سادهتر است، برای ضرب کردن استفاده کنید.
ضرب اعداد اعشاری به کمک نمایش کسری
عدد اعشاری ۰٫۲۰ را در نظر بگیرید. به راحتی میتوانیم این عدد را به کسر متعارفی تبدیل کرده و به صورت یک کسر بنویسیم.
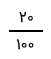
نکته: میدانیم که ۰٫۲ و ۰٫۲۰ هر دو یک عدد هستند ولی اولی را دو دهم و بعدی را بیست صدم میخوانیم.
برای ضرب ۰٫۳۰ در ۰٫۲۰ نیز همین کار را انجام داده و ۰٫۳۰ را به صورت کسر متعارفی نوشته و در هم ضرب میکنیم. به یاد دارید که هنگام ضرب دو کسر، صورتها در هم و مخرجها نیز در هم ضرب میشوند.
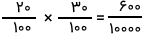
همانطور که میبینید حاصل به صورت ۶۰۰ دههزارم مشخص شده که پس از سادهسازی به شکل ۰٫۰۶ درخواهد آمد. به این ترتیب دو صفر از صورت و دو صفر از مخرج را با هم ساده کردهایم ولی در حقیقت هم صورت و مخرج این کسر را به ۱۰۰ تقسیم کرده و نتیجه را نمایش دادهایم. حال که روش کار را فراگرفتید، میتوانیم با چند مسئله موضوع را برای اعداد اعشاری، ادامه دهیم.

مسئله ۱: بستههای کره، بطور متوسط وزنی برابر با ۰٫۲۵ کیلوگرم دارند. وزن ۴ بسته از این کرهها چقدر است؟
راه حل: واضح است که برای پاسخ باید این دو عدد را در هم ضرب کنیم. پس هر دو را به صورت کسر متعارفی نوشته و مانند کسرها در هم ضرب میکنیم. توجه داشته باشید که ۴ را میتوانیم به قرار دادن واحد یعنی عدد ۱ در مخرج و قرار دادن ۴ در صورت، به شکل کسر متعارفی درآوریم.
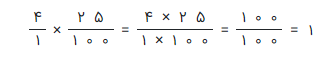
مسئله 2: حاصل 1٫54 × 2٫3 را مشخص کنید؟
راه حل: ابتدا هر دو عدد را به کسر متعارفی تبدیل میکنیم.
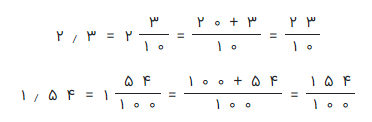
به این ترتیب حاصل ضرب آنها به شکل کسری مانند رابطه زیر خواهد بود.
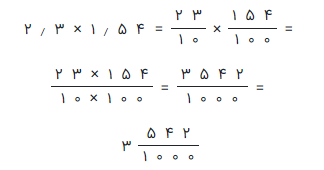
در نهایت مقدار حاصل ضرب را به صورت ۳٫542 مینویسیم و میخوانیم سه ممیز پانصد و چهل و دو هزارم.
مسئله ۳: حاصل ۲٫۰4 × ۶٫3 را مشخص کنید؟
راه حل: اینبار هم در اول کار، هر دو عدد را به کسر متعارفی تبدیل میکنیم.
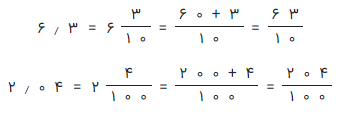
پس از انجام عملیات ضرب، کسر حاصل را به صورت اعشاری در میآوریم.
هر چند این روش برای محاسبه ضرب دو عدد اعشاری ساده به نظر میرسد، ولی یک روش طولانی محسوب میشود زیرا یکبار باید اعداد اعشاری را به کسر تبدیل کرده و ضرب را انجام دهیم. در انتها هم باید حاصل ضرب را به عدد اعشاری تبدیل کنیم.
ضرب اعداد اعشاری به کمک مساحت شکل هندسی
به یاد دارید که مساحت مربع یا مستطیل از طریق ضرب طول در عرض بدست میآید. بنابراین همین خاصیت و رابطهای که برای نمایش اعداد اعشاری (یا کسری) بوسیله تقسیم یک شکل داریم، ضرب اعشاری را اجرا میکنیم. یک مربع را در نظر بگیرید که ۱۰ ستون و ۱۰ سطر دارد. در نتیجه مشخص است که این شکل، دارای ۱۰۰ سلول یا خانه است.
به تعداد مقدار اعشار، خانههای این جدول را به صورت ستون به ستون، رنگی میکنیم. همین کار را برای مضرب دوم ولی براساس سطر به سطر از خانههای جدول انجام میدهیم. تعداد خانههایی مربوط به هر دو رنگ (مشترک بین دو عدد) حاصلضرب آنها را نشان میدهد. به یاد داشته باشید، چون جدول را با ۱۰۰ خانه ساختهاید، اعداد اعشاری را برحسب صدم اعشار بیان کنید. برای مثال مقدار ۰٫۲ را به صورت ۰٫۲۰ (بیست صدم) مشخص کنید.
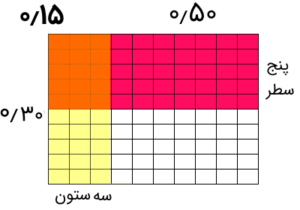
مسئله ۴: حاصل ضرب ۰٫۴ را در ۰٫۵ بدست آورید.
راه حل: ابتدا یک جدول با ۱۰ سطر و ۱۰ ستون میسازیم تا ۱۰۰ خانه حاصل شود.
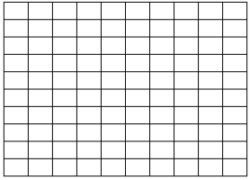
حالا مضرب اول را با رنگآمیزی ستونی مشخص میکنیم. واضح است که ۰٫۴ به صورت ۰٫۴۰ در نظر گرفته شده و ۴۰ خانه از سلولهای جدول را از سمت چپ به ترتیب ستون به ستون رنگ میکنیم. پس ۴ ستون اول مثلا به رنگ زرد در خواهد آمد. مشخص است که چهار ستون دهتایی برابر با ۴۰ بوده که چون کل تقسیمات برابر با ۱۰۰ است، عدد ۰٫۴۰ مشخص شده است.
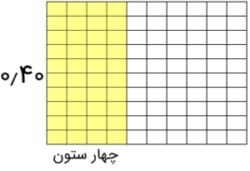
مضرب دوم را هم به همین ترتیب ولی براساس رنگآمیزی سطر به سطر، از جدول اولیه میسازیم. به تصویر زیر دقت کنید که عدد ۰٫۵۰ را نمایش میدهد.
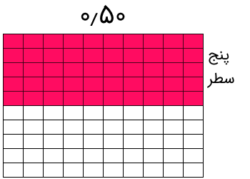
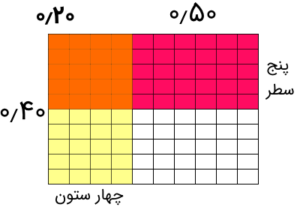
حال این دو شکل را روی هم قرار میدهیم و تعداد خانههای مشترک هر دو رنگ را میشماریم. تعداد برابر است با ۲۰ خانه، پس حاصل ضرب این دو عدد برابر با ۰٫۲۰ یا همان ۰٫۲ است. به تصویر زیر توجه کنید.
مسئله ۵: عدد ۱٫۳ را در ۰٫۵ ضرب کنید.
را حل: در این مسئله یک بخش از مضارب، شامل یک رقم صحیح است. بنابراین ضرب را به صورت زیر تفکیک میکنیم.
۱٫۳ × ۰٫۵ = ( ۱ + ۰٫۳ ) × ۰٫۵ = (۱ × ۰٫۵) + ( ۰٫۳ × ۰٫۵)
هر بخش را جداگانه توسط شکل بدست آورده و نتیجه را با هم جمع میکنیم. ابتدا ۱ را در ۰٫۵ ضرب میکنیم. برای نمایش عدد ۱ ( که به صورت ۱٫۰۰ نیز قابل نمایش است) باید تمام خانههای این جدول ۱۰۰تایی را رنگ کنیم. سپس ۵ سطر اول که رنگی هستند را روی جدول اولیه قرار داده و تعداد خانههای مشترک را میشماریم.
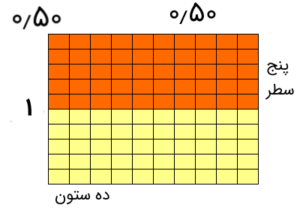
مشخص است که حاصل ضرب اول برابر با ۰٫۵ و حاصل ضرب دوم برابر با ۰٫۱۵ است. بقیه مراحل به مانند مسئله قبل صورت میگیرد.
به این ترتیب مقدار نهایی برای ضرب این دو عدد به صورت زیر درخواهد آمد.
۱٫۳ × ۰٫۵ = ۰٫۵۰ + ۰٫۱۵ = ۰٫۶۵
مسئله 6: عدد ۱٫۳ را در 2٫۵ ضرب کنید.
را حل: در این مسئله هر دو بخش از مضارب، شامل یک رقم صحیح است. بنابراین ضرب را به صورت زیر تفکیک میکنیم.
۱٫۳ × 1٫۵ = ( ۱ + ۰٫۳ ) × ( 2 + ۰٫۵) = ( ۱ × 2 ) + ( 1 × ۰٫۵) + ( 0٫۳ × 2 ) + (۰٫۳ × ۰٫۵)
هر بخش را جداگانه توسط شکل بدست آورده و نتیجه را با هم جمع میکنیم. ابتدا ۱ را در ۲ ضرب میکنیم که حاصل ضرب برابر با ۲ میشود. سپس ۱ را در ۰٫۵ به مانند حالت قبل ضرب میکنیم که میدانیم حاصل برابر با ۰٫۵ است.
برای ضرب کردن ۲ در ۰٫۳، دو جدول ۱۰۰ خانهای ایجاد میکنیم (اگر به جای ۲ مثلا ۴ داشتیم، چهار جدول میساختیم). حالا روی هر دو جدول حاصل ضرب ۱ در ۰٫۳ را محاسبه میکنیم و نتایج را با هم جمع میکنیم. واضح است که مقدار ۰٫۶ بدست میآید زیرا ۶۰ خانه از هر دو جدول (۳۰ خانه از جدول اول و ۳۰ خانه از جدول دوم) رنگآمیزی شدهاند. از طرفی حاصل ضرب ۰٫۵ در ۰٫۳ نیز برابر با ۰٫۱۵ است. بنابراین نتایج را با هم جمع کرده و به مقدار زیر خواهیم رسید.
۱٫۳ × 1٫۵ = ( ۱ × 2 ) + ( 1 × ۰٫۵) + ( 0٫۳ × 2 ) + (۰٫۳ × ۰٫۵)
= 2 + 0٫۵ + ۰٫۶ + ۰٫۱۵ = ۳٫۲۵
مسئله 7: عدد ۳٫۳ را در ۲٫۲ ضرب کنید.
راه حل: از آنجایی که هر دو عدد با یک رقم اعشار ساخته شدهاند، باز هم خانههایی یک جدول ۱۰۰ تایی کافی است. فقط ابتدا بهتر است ضرب را به صورت زیر تجزیه کنیم و بعد براساس رنگآمیزی جدول، حاصلضرب را بدست آوریم.
۲٫۲ × ۳٫۳ = ( ۲ + ۰٫۲) × (3 + 0٫۳) =
۲ × ( ۳ + ۰٫۳) + ۰٫۲ × ( ۳ + ۰٫۳) =
[(۲ × ۳) + (۲ × ۰٫۳)] + [(۰٫۲ × ۳) + (۰٫۲ × ۰٫۳)] =
6 + ۰٫۶ + ۰٫۶ + ۰٫۰۶ = ۷٫۲۶
واضح است که از جدول و رنگآمیزی فقط برای بخشهایی از ضرب استفاده میکنیم که یکی از مضربها، اعشاری باشد.

مسئله 8: مسئله ۳ را به کمک تجزیه اعداد اعشاری به بخشهای صحیح و اعشاری حل کنید.
راه حل: ابتدا هر یک از مضربها را به بخشهای صحیح و اعشاری تفکیک میکنیم.
۲٫۰4 × ۶٫3 = ( ۲ + ۰٫۰۴) × (۶ + 0٫۳) =
۲ × ( ۶ + ۰٫۳) + ۰٫۰۴ × ( ۶ + ۰٫۳) =
[(۲ × ۶) + (۲ × ۰٫۳)] + [(۰٫۰۴ × ۶) + (۰٫۰۴ × ۰٫۳)] =
۱۲ + ۰٫۶ + ۰٫۲۴ + ۰٫۰۱۲ = ۱۲٫852
حتما میدانید که یک عدد اعشاری دارای دو بخش قبل از ممیز (سمت چپ) و بعد از ممیز (سمت راست) تفکیک میشود. بنابراین برای بدست آوردن حاصل ضرب مسئله ۳، چهار ضرب را انجام میدهیم. قسمت صحیح عدد اول در قسمت صحیح عدد دوم، قسمت صحیح عدد اول در قسمت اعشاری عدد دوم، قسمت اعشاری عدد اول در قسمت صحیح عدد دوم و ضرب قسمت اعشاری عدد اول در قسمت اعشاری عدد دوم. در آخر کافی است برای رسیدن به پاسخ نهایی، این مقادیر را با هم جمع کنیم.
ضرب اعداد اعشاری به کمک قاعده ضرب
به کمک قاعده ضرب اعداد اعشاری، میتوان به راحتی ضرب چنین اعدادی را انجام داد. این قاعده به صورت زیر است.
برای ضرب دو عدد اعشاری، ابتدا آن دو عدد را بدون در نظر گرفتن ممیز، در هم ضرب کرده، سپس به جمع تعداد ارقام اعشار هر دو عامل ضرب، از سمت راست عدد حاصلضرب ممیز را جابجا کرده و به سمت چپ میبریم. به مسئله زیر دقت کنید.
مسئله 9: فرض کنید قرار است حاصل ضرب ۳۵٫۲۵ را در ۱۰٫۰۳ بدست آوریم.
راه حل: ابتدا برای انجام ضرب اعداد اعشاری آنها را بدون ممیز در هم ضرب میکنیم.
3525× 1003 = 3535575
از آنجایی که مضرب اول، دو رقم اعشار و مضرب دوم نیز دو رقم اعشار دارد، مجموع تعداد ارقام اعشار هر دو عدد برابر با ۴ شده و از سمت راست حاصلضرب قسمت بالا، ممیز را چهار رقم به سمت چپ حرکت میدهیم. میدانید که عدد صحیح را میتوان با یک ممیز و صفر در سمت راست آن نیز نمایش داد. پس عدد مورد نظر به شکل ۳۵۳۵۵۷۵٫۰ در نظر گرفته شده و ممیز جابجا میشود.
۳۵۳۵۵۷٫۵ :حرکت اول
۳۵۳۵۵٫۷۵ :حرکت دوم
۳۵۳۵٫۵۷۵ :حرکت سوم
۳۵۳٫۵۵۷۵ :حرکت چهارم
پس حاصل برابر است با ۳۵۳٫۵۵۷۵ یا سیصد و پنجاه و سه ممیز پنج هزار و پانصد هفتاد و پنج، ده هزارم.
مسئله 10: در جای خالی عدد مناسب بنویسید.
۰٫۲ × ۰٫۴ = ــــ × ــــ = ــــ
راه حل: میبینید که باید ضرب را به صورت کسری انجام دهیم. بنابراین هر کدام از آنها را به صورت کسر متعارفی در میآوریم.
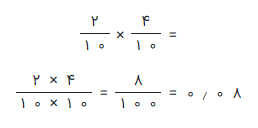
مسئله ۱۱: برای حاصل ضرب، عاملهای ضرب متفاوتی بنویسید.
ـــــ × ـــــ = ۰٫۴
راه حل: شاید سادهترین مضرب ۰٫۴، همان ۱ باشد. در نتیجه عبارت بالا را به صورت زیر خواهیم نوشت.
۰٫۴ = ۰٫۴ × ۱
از طرفی رابطه زیر نیز برقرار است.
۰٫۴ = ۰٫۰۴ × ۱۰
همچنین داریم:
۰٫۴ = ۰٫۰۰۴ × ۱۰۰
به این ترتیب ۰٫۴ را به سه روش حاصلضربی نوشتیم. همچنین میتوانیم عوامل دیگری برای ضرب نیز ارائه کنیم.
۰٫۴ = ۰٫۲ × ۲
یا
۰٫۴ = ۰٫5 × 8
مسئله ۱۲: مساحت شکل زیر را پیدا کنید.
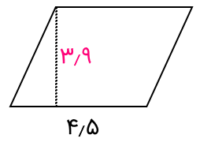
نکته: توجه داشته باشید که این شکل، یک متوازی الاضلاع است و مساحت آن برابر است با قاعده در ارتفاع آن.

راه حل:
با توجه به توضیح بالا، باید ضرب اعداد اعشاری را برای دو مقدار ۳٫۹ را در ۴٫۵ به کار ببریم. برای این کار از شیوه ضرب ساده و تبدیل به عدد صحیح کمک میگیریم.
۴۵ × ۳۹ = ۱۷۵۵
از آنجایی که هر دو عدد یک رقم اعشار داشتند، مجموع تعداد ارقام اعشار آنها برابر با ۲ است. پس از سمت راست، دو رقم اعشار ایجاد میکنیم. نتیجه برابر با ۱۷٫۵۵ خواهد بود. پس مساحت متوازی الاضلاع ذکر شده، ۱۷٫۵۵ واحد است.
همانطور که دیدید، راهکار سوم که برای ضرب اعداد اعشاری بیان شد، سادهتر از همه به نظر میرسد ولی دقت کنید که برای این روش، ما مفاهیمی را که در دو قسمت قبلی فراگرفتیم، در نظر گرفته و به کار بردهایم. در بسیاری از مواقع، انجام ضرب ذهنی و سریع میتواند برای مقادیر اعشاری نیز به کار آید. برای مثال مشخص است که ضرب هر عدد اعشاری در ۱۰ یا توانهایی از ۱۰، باعث حرکت اعشار به سمت راست خواهد شد.
خلاصه و جمعبندی
در این متن به مفهوم ضرب اعداد اعشاری توجه کردیم و روشهای مختلف برای ضرب کردن دو عدد اعشاری را فراگرفتیم. همانطور که در متن اشاره شد، به روش ضرب کسرها، مساحت مستطیل و همچنین قاعده ضرب اعشاری میتوان ضرب عدد های اعشاری را انجام داد. تفاوتی بین نتیجه حاصل از این روشها وجود ندارد و هر کدام که مورد استفاده قرار گیرند، پاسخ یکسانی با روشهای دیگر دریافت خواهید کرد. ولی مهم آن است که این مفاهیم را یاد بگیرید و برای پاسخ به یک مسئله، هر کدام که سادهتر بود، به کار ببرید. در نوشتارهای بعدی مجله فرادرس به موضوع جمع، تفریق و تقسیم اعشاری نیز خواهیم پرداخت.
آزمون ضرب اعداد اعشاری
۱. کدام ویژگی از ضرب اعداد اعشاری باعث میشود جابهجایی جای عددها در عبارت تاثیری بر نتیجه نگذارد؟
خاصیت توزیعی ضرب اعشاری ترتیب عددها را مهم میکند.
خاصیت جابجایی در ضرب اعشاری باعث ثابت ماندن حاصل میشود.
خاصیت پخشی ضرب اعشاری تغییر حاصل را مانع میشود.
خاصیت جمعپذیری ضرب اعشاری در ترتیب عددها اثر دارد.
خاصیت جابجایی در ضرب اعشاری، تضمین میکند که جای عددها هر طور عوض شود، حاصل تغییری نمیکند. در روشهای ضرب اعشاری این ویژگی همیشه وجود دارد و تغییر ترتیب عددها تاثیری روی جواب ندارد. گزینههایی مانند «خاصیت پخشی»، «خاصیت جمعپذیری» و «خاصیت توزیعی» یا به ضرب اعشاری مرتبط نیستند یا تاثیرگذاری مستقیم روی ترتیب عددها و نتیجه ضرب ندارند.
۲. در مدل هندسی جدول ۱۰۰ خانهای برای ضرب اعشاری، ناحیه مشترک بین دو رنگ چه مفهومی را در ضرب اعداد اعشاری نشان میدهد؟
مقدار حاصل ضرب اعشاری دو عدد را نمایش میدهد.
تعداد بخشهای صحیح اعداد مضروب را نشان میدهد.
جمع ارقام اعشاری هر دو عدد را مشخص میکند.
تعداد خانههای مختلف رنگآمیزی شده را جدا از هم نشان میدهد.
در مدل هندسی جدول ۱۰۰ خانهای، ناحیه مشترک رنگآمیزی شده نمایانگر «مقدار حاصل ضرب اعشاری دو عدد» است. این بخش از جدول نشان میدهد چه مقدار از جدول بر اساس ترکیب دو عدد اعشاری پر شده است.
۳. در روش قاعده ضرب اعشاری، چگونه محل ممیز در پاسخ نهایی تعیین میشود؟
محل ممیز با حذف ممیز هر دو عدد و قرار دادن ممیز در انتهای پاسخ تعیین میشود.
محل ممیز بر طبق مجموع تعداد ارقام اعشاری هر دو عدد عامل در جواب نهایی انتخاب میشود.
محل ممیز براساس ترتیب ضرب اعداد از چپ به راست تعیین میشود.
محل ممیز بر اساس مجموع ارقام صحیح دو عدد در پاسخ مشخص میشود.
در قاعده ضرب اعشاری، ابتدا اعداد بدون ممیز در هم ضرب میشوند و سپس تعداد ارقام اعشاری هر دو عدد با هم جمع میگردد. ممیز نهایی به اندازه مجموع این ارقام از سمت راست در پاسخ نوشته میشود.
۴. در محاسبه وزن چند بسته بر اساس ضرب اعشاری با تبدیل به کسر متعارفی، کدام گامهای زیر باید دنبال شوند؟
هر عدد اعشاری را به کسر متعارفی تبدیل، کسرها را ضرب و نتیجه را مجددا به اعشاری برگردانید.
هر دو عدد اعشاری را به عدد صحیح تبدیل و سپس ضرب کنید.
اعداد اعشاری را به درصد تبدیل و درصدها را جمع بزنید.
تنها صورتهای کسر را ضرب و مخرجها را ثابت نگه دارید.
در این روش برای ضرب اعشاری باید ابتدا هر عدد اعشاری را به یک کسر متعارفی تبدیل کرد. سپس کسرها را ضرب نموده و پس از سادهسازی در صورت نیاز، نتیجه را مجددا به عدد اعشاری بازگرداند. راهحلهایی مانند تبدیل به عدد صحیح یا درصد یا ضرب صرفِ صورتها خطا دارند و روش صحیح را ارائه نمیدهند.
۵. حاصل ضرب دو عدد ۰٫۲۴ و ۳٫۶ را به دست آورید.
۰٫۸۶۴
۰٫۰۸۶۴
۸٫۶۴
۰٫۰۰۶۴
ابتدا اعشار اعداد را نادیده گرفته و حاصل ضرب ۲۴ و ۳۶ را به دست میآوریم و پاسخ آن ۸۶۴ به دست میآید. مجموع ارقام اعشار این دو عدد ۳ رقم است، پس ممیز اعشار را سه رقم از سمت راست جدا کرده و حاصل ۰٫۸۶۴ به دست میآید.













ضرب ۱٫۱در۱٫۱ را توضیح میدین
با سلام خدمت شما؛
برای ضرب این دو عدد بهتر است ۱٫۱ را به شکل ۱ + ۰٫۱ بنویسید. سپس دو پرانتز شامل ۱ + ۰٫۱ را در هم ضرب کنید.
از همراهی شما با مجله فرادرس سپاسگزاریم.
ببخشید ما توی کلاس هقتم ضرب درصد در اعشار داریم توضیح اون رو چرا نذاشتین
با سلام و وقت بخیر؛
روشهای توضیح داده شده در این مطلب، برای ضرب درصد در اعشار نیز قابل استفاده هستند.
از همراهی شما با مجله فرادرس سپاسگزاریم.
عالی بود
ببخشید ضرب ۲۰ در ۳۰ آیا ۶۰۰ نمی شود؟ شما ۶۰ نوشته اید
با سلام و وقت بخیر؛
مقاله اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم
واقعاااااااااااااااااا عالی بود ممنونم ازتون
عالی بود
ممنون بسیار خوب و واضح توضیح دادین.