سیستم LTI — از صفر تا صد

سیستم LTI یا سیستم خطی تغییرناپذیر با زمان، نوعی از سیستم‌ها است که هم خطی و هم تغییرناپذیر با زمان است. سیستم‌های خطی سیستم‌هایی هستند که خروجی آن‌ها برای ترکیبی خطی از ورودی‌ها برابر با ترکیبی خطی از پاسخ به تک تک آن ورود‌ی‌ها باشد. سیستم‌های تغییرناپذیر با زمان نیز سیستم‌هایی هستند که خروجی آن‌ها به اینکه ورودی چه زمانی اعمال شود، بستگی ندارد. این ویژگی‌ها موجب می‌شود درک و نمایش سیستم‌های LTI  آسان باشد.

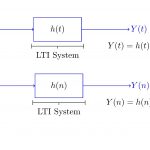
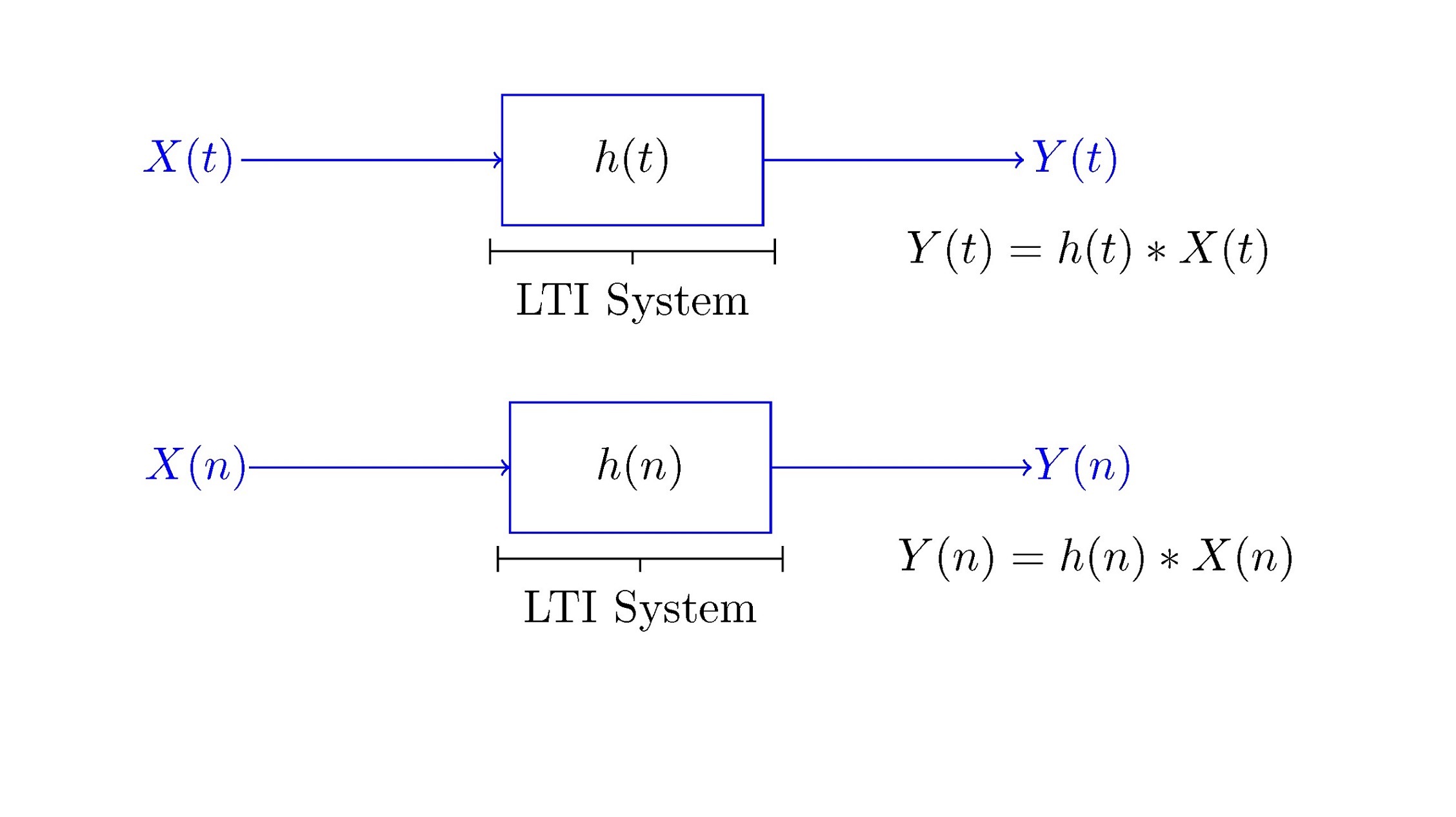
مزیت سیستم‌های خطی تغییرناپذیر با زمان نسبت به ماشین‌های حالت (State Machine) ساده قابلیت نمایش آن‌ها است. این سیستم‌ها بر خلاف ماشین‌های حالت، دارای حافظه از حالت‌های گذشته هستند و توانایی پیش‌بینی آینده را نیز دارند. سیستم‌های LTI برای پیش‌بینی رفتار طولانی مدت در یک سیستم مورد استفاده قرار می‌گیرند، بنابراین آن‌ها غالبا برای مدل کردن سیستم‌هایی مانند سیستم‌های قدرت مناسب هستند. کاربرد مهم دیگر سیستم‌های خطی تغییرناپذیر با زمان در مدارهای الکتریکی است. این مدارها که اکثرا از ترانزیستور، مقاومت و سلف ساخته می‌شوند، پایه و اساس تکنولوژی‌های مدرن هستند.

در این مطلب به توضیح سیستم‌های خطی تغییرناپذیر با زمان می‌پردازیم، مشخصه‌های این سیستم‌ها را شرح می‌دهیم و چند مثال از سیستم‌های خطی تغییرناپذیر با زمان پیوسته و گسسته را ارائه می‌کنیم.

مشخصه‌های سیستم LTI

در این بخش، در مورد خطی و نامتغیر با زمان بودن سیستم LTI بحث می‌کنیم.

سیستم خطی

مشخصه سیستم‌های خطی این است که خروجی آن‌ها به صورت خطی به ورودی وابسته است و تغییر خطی در ورودی باعث ایجاد تغییر در خروجی به همان صورت خواهد شد. پس اگر ورودی $$x_1(t)$$ باعث تولید خروجی $$y_1(t)$$ و ورودی $$x_2(t)$$ باعث ایجاد خروجی $$y_2(t)$$ شود، آنگاه ترکیب خطی از این ورودی‌ها باعث تولید ترکیب خطی از همین خروجی‌ها خواهد شد.

فیلم آموزش کنترل مدرن – حل ۱۰۰ مساله در فرادرس

کلیک کنید

مثلا ورودی $$\big(x_1(t) + x_2(t)\big)$$ باعث تولید خروجی $$\big(y_1(t) + y_2(t)\big)$$ خواهد شد. علاوه بر این ورودی $$\big(a_1 \cdot x_1(t) + a_2 \cdot x_2(t)\big)$$ باعث ایجاد خروجی $$(a_1 \cdot y_1(t) + a_2 \cdot y_2(t))$$ می‌شود.

به عبارت دیگر برای یک سیستم T در طول زمان t و ترکیبی از سیگنال‌های ورودی $$x_1(t)$$ و $$x_2(t)$$ و خروجی‌های $$y_1(t)$$ و  $$y_2(t)$$ داریم:

$$T\big[a_1x_1(t) + a_2x_2(t)\big] = a_1T\big[x_1(t)\big] + a_2T\big[x_2(t)\big] = a_1y_1(t) + a_2y_2(t)$$

که در آن $$a_1$$ و $$a_2$$ ثابت هستند. نکته مهم دیگر این است که خروجی یک سیستم خطی برای ورودی صفر برابر با صفر است.

سیستم نامتغیر با زمان

سیستم نامتغیر با زمان سیستمی است که خروجی برای یک ورودی خاص، به زمان اعمال آن ورودی وابسته نیست. یک سیستم نامتغیر با زمان که ورودی $$x(t)$$ را دریافت و خروجی $$y(t)$$ را تولید می‌کند، زمانی که ورودی $$x(t+\sigma)$$ به آن اعمال شود، خروجی شیفت یافته $$y(t+\sigma)$$ را تولید می‌کند.

بنابراین، سیستم‌های خطی تغییرناپذیر با زمان توسط یک تابع یکتا در حوزه زمان قابل توصیف هستند که به آن پاسخ ضربه سیگنال می‌گویند. برای یک ورودی تصادفی، خروجی یک سیستم برابر با کانولوشن (Convolution) سیگنال ورودی با پاسخ ضربه سیستم است.

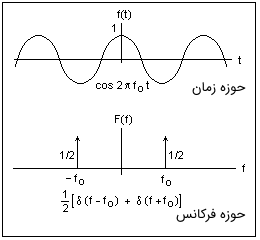
یک سیستم LTI توسط تابع تبدیل آن نیز قابل توصیف است. تابع تبدیل در واقع تبدیل لاپلاس پاسخ ضربه سیستم است. این تبدیل، تابع را از حوزه زمان به حوزه فرکانس می‌برد. اهمیت تابع تبدیل در این نکته است که معادلات تفاضلی را به معادلات جبری و کانولوشن را به ضرب تبدیل می‌کند. در حوزه فرکانس، خروجی برابر با حاصل ضرب تابع تبدیل در ورودی تبدیل یافته است. انتقال از حوزه زمان به فرکانس در شکل زیر به تصویر کشیده شده است.

علاوه بر خطی بودن و تغییرناپذیری با زمان، سیستم‌های LTI سیستم‌هایی دارای حافظه، معکوس‌پذیر، حقیقی، پایدار و علّی (Casual) هستند. علّی بودن به این معنی است که این سیستم‌ها فقط به وقایع لحظه حال و گذشته بستگی دارند و پایداری به این معنی است که برای ورودی محدود، خروجی محدود تولید می‌کنند. به دلیل مشخصه‌های سیستم‌های خطی تغییرناپذیر با زمان، شکل عمومی یک سیستم LTI با خروجی $$y[n]$$ و ورودی $$x[n]$$ در زمان $$n$$ و ثابت‌های $$c_K$$ و $$d_j$$ به صورت زیر تعریف می‌شود:

$$y[n] = c_0y[n-1] + c_1y[n-2] + ... + c_{k-1}y[n-k] + d_0x[n] + d_1x[n-1] + ... + d_jx[n-j]$$

وضعیت این سیستم به مقادیر $$k$$ خروجی قبلی و $$j$$ ورودی قبلی وابسته است. به دلیل مشخصه خطی بودن، خروجی در زمان $$n$$ یک ترکیب خطی از خروجی‌های قبلی، ورودی‌های قبلی و ورودی زمان حال است.

اگر یک رشته از سیستم‌های خطی تغییرناپذیر با زمان به صورت پشت سر هم به یکدیگر متصل شوند، خروجی سیستم جدید به مرتبه این اتصال بستگی ندارد. این مشخصه از ویژگی شرکت‌پذیری (Associative) و مشخصه تعویض‌پذیری (Commutative) ناشی می‌شود.

می‌توان شکل عمومی یک سیستم خطی تغییرناپذیر با زمان را به صورت معادله عملگر بازنویسی و سپس با تغییراتی جزئی آن را به یک معادله مفیدتر تبدیل کرد:

$$\begin{aligned} Y &= c_0\mathcal{R}Y + c_1\mathcal{R}^2Y + \cdots + c_{k-1}\mathcal{R}^{k}Y + d_0X + d_1\mathcal{R}X + \cdots + d_j\mathcal{R}^jX \\ &= Y\big(c_0\mathcal{R} + c_1\mathcal{R}^2 + \cdots + c_{k-1}\mathcal{R}^{k}\big) + X\big(d_0 + d_1\mathcal{R} + \cdots + d_j\mathcal{R}^j\big) \end{aligned}$$

که با معادله زیر یکسان است:

$$Y\big(1 - c_0\mathcal{R} - c_1\mathcal{R}^2 - ... - c_{k-1}\mathcal{R}^{k}\big) = X\big(d_0 + d_1\mathcal{R} + \cdots + d_j\mathcal{R}^j\big)$$

سپس می‌توان یک تقسیم انجام داد تا معادله‌ای به دست آید که حاصل تقسیم خروجی بر ورودی را توصیف کند:

$$\frac{Y}{X} = \frac{d_0 + d_1\mathcal{R} + \cdots + d_j\mathcal{R}^j}{1 - c_0\mathcal{R} - c_1\mathcal{R}^2 - ... - c_{k-1}\mathcal{R}^{k}}$$

معادله بالا، تابع سیستم مربوط به سیستم خطی تغییرناپذیر با زمان است و معمولا به صورت یک چند جمله‌ایی به صورت زیر نوشته می‌شود:

$$\frac{Y}{X} = \frac{b_0 + b_1\mathcal{R} + b_2\mathcal{R}^2 + \cdots}{a_0 + a_1\mathcal{R} + a_2\mathcal{R}^2 + \cdots}$$

توجه کنید که صورت و مخرج چند جمله‌ای از درجه $$R$$ (متغیر تاخیر) هستند. درک تاثیر صورت و مخرج، اهمیت بسیاری در تحلیل یک سیستم دارد.

پاسخ ضربه

پاسخ ضربه یک مشخصه بسیار مهم در سیستم‌های خطی تغییرناپذیر با زمان است. از پاسخ ضربه می‌توان برای توصیف یک سیستم LTI و پیش‌بینی خروجی سیستم برای هر ورودی داده شده، استفاده کرد. برای یافتن پاسخ ضربه، باید از سیگنال ضربه واحد استفاده کنیم. سیگنال ضربه واحد کاربردهای بسیار زیادی در نمونه‌برداری دارد. این سیگنال مقدار یک (1) را در لحظه صفر تولید می‌کند و در سایر لحظات مقدار آن صفر است. تعریف تابع پاسخ ضربه یک سیستم به این صورت است: برای یک سیستم LTI، زمانی که ورودی سیستم سیگنال ضربه واحد ($$\sigma(t)$$) باشد، پاسخ ضربه برابر با خروجی $$y(t)$$ است.

در واقع، تابع ضربه سیستم‌های خطی تغییرناپذیر با زمان به این مسئله می‌پردازد که اگر یک ورودی سیگنال واحد در یک زمان مشخص وارد شود، خروجی سیستم در زمان‌های بعدی به چه صورت خواهد بود؟ می‌توان پاسخ ضربه را به سادگی و با اعمال یک سیگنال ضربه و مشاهده آنچه که اتفاق می‌افتد، به دست آورد.

کانولوشن

کانولوشن، یک نمایش از سیگنال به صورت ترکیبی خطی از سیگنال‌های ورودی تاخیر یافته است. به عبارت دیگر، سیگنال به ورودی‌هایی تجزیه می‌شود که برای ساخت آن مورد استفاده قرار می‌گیرند. کانولوشن بین سیگنال‌های پیوسته در زمان و سیگنال‌های گسسته در زمان به صورت متمایز به کار می‌رود. سیگنال‌های گسسته در زمان، یک ترکیب خطی از ضربه‌های گسسته هستند، پس می‌توان آن‌ها را به صورت مجموع کانولوشن نمایش داد. از طرف دیگر، سیگنال‌های پیوسته در زمان مانند محاسبه مساحت زیر یک نمودار، مقادیری پیوسته هستند، پس این سیگنال‌ها به انتگرال کانولوشن نیاز دارند.

مجموع کانولوشن به شکل زیر نمایش داده می‌شود:

$$y[n] = \sum_{k = -\infty}^{\infty}x[k]\, h[n - k]$$

اما انتگرال کانولوشن به صورت زیر است:

$$y(t) = \int_{-\infty}^{\infty}h(\tau)x(t-\tau)\,d\tau = x(t) \ast h(t)$$

توجه کنید که $$*$$ نماد ریاضی کانولوشن را نشان می‌دهد.

تمام سیستم‌های خطی تغییرناپذیر با زمان را می‌توان با کمک تابع ضربه و انتگرال یا جمع کانولوشن توصیف کرد. خروجی هر سیستم LTI می‌تواند با استفاده از ورودی و تابع ضربه برای آن سیستم، محاسبه شود. کانولوشن دارای مشخصه‌های مهم زیر است:

1. خاصیت جابه‌جایی (Commutativity): $$x(t) \ast h(t) = h(t) \ast x(t)$$
2. خاصیت شرکت‌پذیری (Associativity): $$\big[x(t) \ast h_1(t)\big] \ast h_2(t) = x(t) \ast \big[h_1(t) \ast h_2(t)\big]$$
3. خاصیت توزیع‌پذیری جمع (Distributivity of Addition): $$x(t) \ast \big[h_1(t) + h_2(t)\big] = x(t) \ast h_1(t) + x(t) \ast h_2(t)$$
4. عنصر یکه یا همانندی (Identity Element): $$x(t) \ast h(t) = h(t)$$

تابع تبدیل

تابع تبدیل یک سیستم با تبدیل لاپلاس گرفتن از پاسخ ضربه سیستم به دست می‌آید و اطلاعات با ارزشی راجع به رفتار سیستم ارائه می‌کند. همچنین موجب تسهیل محاسبات پاسخ خروجی می‌شود.

تعریف تابع تبدیل

اگر پاسخ ضربه برای یک سیستم با خروجی $$y(t)$$ توسط $$h(t)$$ نشان داده شود، آنگاه تابع تبدیل سیستم داده شده برابر است با: $$H(S) = \mathcal{L}(h(t))$$

مثال

معادله یک سیستم علی LTI به صورت زیر داده شده است:

$$\ddot{y(t)} + \dot{y(t)} = x(t)$$

پاسخ ضربه سیستم را با جایگذاری $$x(t)$$ با $$\sigma(t)$$ و گرفتن تبدیل لاپلاس از آن به دست می‌آوریم.

$$y(t) = h(t) = \mathcal{L}^{-1}(\frac{1}{s^2 + s}) = u(t) - e^{-t}$$

برای این معادله دیفرانسیل تابع تبدیل به صورت زیر است:

$$H(S) = \frac{1}{s^2 + s}$$

همان‌طور که قبلا گفتیم، یک سیستم LTI می‌تواند به صورت زیر نوشته شود:

$$\frac{Y}{X} = \frac{b_0 + b_1\mathcal{R} + b_2\mathcal{R}^2 + \cdots}{a_0 + a_1\mathcal{R} + a_2\mathcal{R}^2 + \cdots}$$

بنابراین تابع تبدیل یک سیستم علی و LTI نیز به صورت زیر خواهد بود:

$$\frac{Y(S)}{X(S)} = \frac{a_0 + a_1\mathcal{S} + a_2\mathcal{S}^2 + \cdots}{b_0 + b_1\mathcal{S} + b_2\mathcal{S}^2 + \cdots}$$

تابع تبدیل و خروجی

خروجی یک سیستم خطی تغییرناپذیر با زمان، توسط کانولوشن سیگنال ورودی با پاسخ ضربه به دست می‌آید. از آنجایی که کانولوشن در حوزه زمان برابر با ضرب در حوزه لاپلاس است، خروجی $$Y(S)$$ در یک سیستم با تابع تبدیل $$H(S)$$ برای ورودی $$X(S)$$ به صورت زیر خواهد بود:

$$Y(S) = H(S)X(S)$$

حال خروجی در حوزه زمان برابر است با:

$$y(t) = \mathcal{L}^{-1}(Y(S))$$

مثال

خروجی سیستم زیر را به دست آورید:

$$\ddot{y(t)} + \dot{y(t)} = x(t); x(t) = e^t$$

از مثال قبل داریم:

$$H(S) = \frac{1}{s^2 + s}$$

از آنجایی که $$X(S) = \mathcal{L}\{x(t)\} = \frac{1}{S-1}$$، پس:

$$Y(S) = X(S)H(S) = \frac{1}{S(S+1)(S-1)}$$

بنابراین خروجی برابر است با:

$$y(t) = \mathcal{L}^{-1}\{Y(S)\} = \mathcal{L}^{-1}\{\frac{1}{S(S+1)(S-1)}\} = 0.5e^{t} + 0.5e^{-t} - u(t)$$

صفرها و قطب‌ها

از آنجایی که تابع تبدیل توسط تقسیم دو چندجمله‌ایی به دست می‌آید، می‌توانیم از آن چندجمله‌ایی‌ها فاکتور بگیریم:

$$H(S) = \frac{(S + z_0)(S + z_1)(S + z_2)\cdots}{(S + p_0)(S + p_1)(S + p_2)\cdots}$$

فیلم آموزش شناسایی سیستم – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

که در آن $$z_0, z_1, z_2 \cdots$$ صفرهای مختلط سیستم و $$p_0, p_1, p_2 \cdots$$ قطب‌های مختلط سیستم هستند. قطب‌ها و صفر‌ها نیز اطلاعات بسیار جالبی راجع به سیستم و رفتار آن به ما می‌دهند و در کنترل سیستم‌ها مورد استفاده قرار می‌گیرند.

سیستم LTI گسسته

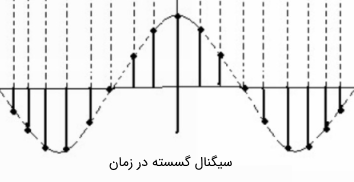
سیگنال‌های گسسته در زمان مجموعه‌ای از سیگنال‌های تکی هستند. این سیگنال‌ها می‌توانند حاصل نمونه‌برداری از یک سیگنال پیوسته در زمان باشند و یا حاصل یک پدیده که در اصل به صورت گسسته است. سیگنال‌های گسسته را می‌توان در یک گراف با نقاط تکی متصل به محور x نشان داد. محور x همان زمان و محور y سیگنال است. همان طور که قبلا اشاره شد، در سیگنال‌های گسسته به جمع کانولوشن برای محاسبه خروجی در هر زمان داده شده نیاز است.

مثال

برای سیستم خطی تغییرناپذیر با زمان زیر با تابع ورودی و تابع پاسخ ضربه داده شده، خروجی سیستم را در زمان n محاسبه کنید. $$u[n]$$ برابر با تابع پله واحد است.

$$\begin{aligned} u[n] &= \begin{cases} 1 & \mbox{if } n \geq 0 \\ 0 & \mbox{if } n \lt 0\end{cases}\\ x[n] &= u[n] \\ h[n] &= 2^nu[n] \end{aligned}$$

پاسخ: برای محاسبه خروجی داریم:

$$y[n] = \sum_{k=-\infty}^{\infty}x[k]\, h[n-k] = \sum_{k=-\infty}^{\infty}u[k]2^{n-k}u[n-k] = 2^n\sum_{k=-\infty}^{\infty}2^{-k}u[k]\, u[n-k]$$

حال نیاز است تا بازه‌های این جمع بررسی شود. زمانی که $$k<0$$، $$x[k]\, k[n-k] = 0$$ خواهد شد، پس می‌توان از مقادیر $$k$$ که کمتر از صفر هستند، صرف نظر کرد. زمانی که $$k<0$$ باشد، دو تابع فقط در بازه $$\{0, n\}$$ هم‌پوشانی دارند، پس باید از این محدوده استفاده کنیم. بنابراین معادله به صورت زیر نوشته می‌شود:

$$\begin{aligned} y[n] &= 2^n\sum_{k=0}^{n}2^{-k} \\ &= 2^n\frac{1 - \frac{1}{2}^{n+1}}{1-\frac{1}{2}} \\ &= \frac{1 - 2^{n+1}}{1 - 2} \\ &= 2^{n+1} - 1 \end{aligned}$$

سیستم LTI پیوسته

سیستم خطی تغییرناپذیر با زمان پیوسته دارای سیگنال‌هایی است که در تمام مقادیر زمانی ممکن تعریف شده‌اند. بنابراین نیاز است از انتگرال کانولوشن استفاده کنیم تا به درستی این نوع از سیستم‌ها را شناسایی و کنترل کنیم.

فیلم آموزش سیستم های LTI در تجزیه و تحلیل سیگنال ها و سیستم ها (رایگان)‎ در فرادرس

کلیک کنید

مثال

فرض کنید یک سیستم خطی تغییرناپذیر با زمان با تابع پاسخ ضربه $$h(t)$$ داریم. می‌خواهیم بدانیم که ورودی $$x(t)$$ چگونه بر این سیستم اثر می‌گذارد. برای این کار، به کانولوشن احتیاج خواهیم داشت. فرض کنید که t بزرگتر از صفر است (در غیر این صورت جواب همیشه صفر خواهد بود). حال باید کانولوشن دو سیگنال را به دست آوریم:

$$\begin{aligned} u(t) &= \begin{cases} 1 & \mbox{if } t \geq 0 \\ 0 & \mbox{if } t \lt 0\end{cases}\\ x(t) &=u(t) \\ h(t) &= e^{-3t}u(t) \end{aligned}$$

کانولوشن دو سیگنال $$x(t) \ast h(t)$$ برابر است با:

$$\int_{-\infty}^{\infty}h(\tau)u(t-\tau)\, d\tau$$

برای یافتن بازه‌های انتگرال، باید توابع را بررسی کرده و بدانیم که در چه لحظاتی دارای مقادیر غیر صفر هستند. $$h(\tau)$$ برای مقادیر سمت چپ محور y یا تمام اعداد منفی صفر می‌شود. $$u(t - \tau)$$ برای تمام مقادیر بزرگتر از $$\tau$$ برابر با صفر است. بنابراین محدوده ما در واقع $$\left\{0,t\right\}$$ است. داخل انتگرال برابر با حاصل ضرب دو سیگنال است (توجه کنید که در اصل مساحت زیر نمودار محاسبه می‌شود). بنابراین داریم:

$$\int_{0}^{t}e^{-3\tau}d\tau = \frac{1}{-3}\left. e^{-3\tau} \right|^{t}_{0} = \frac{1}{-3}\left[e^{-3t} - 1\right]$$