حد در بینهایت – به زبان ساده

در مطالب قبلی وبلاگ فرادرس، حد بینهایت به صورت دقیق مورد مطالعه قرار گرفت. حد بینهایت حالتی را نشان می‌دهد که در آن، حد یک تابع در یک نقطه مشخص برابر با بینهایت شود و کاربرد زیادی در محاسبه مجانب قائم و محاسبه دامنه و برد یک تابع دارد. اما یکی دیگر از مباحث مهم در حد ریاضیات، محاسبه حد در بینهایت است. این مبحث هم‌چنین در تشخیص نوع تابع ناپیوسته بسیار کاربرد دارد.

حد در بینهایت به صورت کلی بیان می‌کند که مقدار حد یک تابع در بینهایت چقدر است. بنابراین با استفاده از این مفهوم می‌توان مشخص کرد که یک تابع در بینهایت به کدام مقدار میل می‌کند. این مفهوم به صورت دقیق در این مطلب به وسیله‌ی مثال‌های متعددی مورد بررسی قرار می‌گیرد.

حد در بینهایت چیست؟

همانطور که اشاره شد، حد در بینهایت نشان دهنده مقدار حد یک تابع در زمانی است که متغیر x به سمت مثبت یا منفی بینهایت میل می‌کند. این موضوع در روابط زیر به خوبی نشان داده شده است.

$$\large \mathop { \lim } \limits _ { x \to \infty } f \left ( x \right ) \hspace { 0.25 in } \hspace { 0.25 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to - \infty } f \left ( x \right )$$

به عبارت دیگر ما به دنبال این هستیم که عملکرد تابع، زمانی که مقدار x به سمت بینهایت میل می‌کند را به صورت دقیق بررسی کنیم. بنابراین ابتدا قوانین مختلف حاکم بر حد در بینهایت را بیان می‌کنیم و برای هرکدام از آن‌ها مثالی را نیز مورد بررسی قرار می‌دهیم.

محاسبه حد در بینهایت

برای انجام محاسبات مختلف مربوط به حد در بینهایت و تسلط بر این مبحث، ابتدا باید نکات مختلفی را مورد بررسی قرار دهیم و سپس کاربرد هرکدام از این نکات را در قالب مثال بیان کنیم.

نکته اولی که باید به آن اشاره کرد این است که روابط ذکر شده در بخش «نکات تکمیلی حد بینهایت» در مطلب «حد بینهایت — به زبان ساده» در این بخش نیز صادق است و تنها کافی است که عبارت $$\mathop { \lim } \limits _ { x \to \, c }$$ را با $$\mathop { \lim } \limits _ { x \to \infty }$$ یا $$\mathop { \lim } \limits _ { x \to - \infty }$$ جایگزین کنیم.

قانون اول

علاوه بر نکاتی که بیان شدند، موارد دیگری نیز حضور دارند که این موارد کاربرد زیادی در مبحث حد در بینهایت دارند. بنابراین در ادامه، دو نکته بسیار مهم دیگری که در اکثر مسائل حد در بینهایت استفاده می‌شوند، مورد بررسی قرار می‌گیرد.

• در صورتی که $$r$$ یک عدد گویای مثبت و $$c$$ یک عدد حقیقی باشد، رابطه زیر در مبحث حد در بینهایت برقرار است.

$$\large \mathop { \lim } \limits _ { x \to \infty } \frac { c } { { { x ^ r } } } = 0$$

• اگر $$r$$ یک عدد گویای مثبت و $$c$$ یک عدد حقیقی باشد و تابع $${ x ^ r }$$ برای xهای منفی ($$x < 0$$) تعریف شده باشد، رابطه زیر در مبحث حد در بینهایت برقرار است.

$$\large \mathop { \lim } \limits _ { x \to - \infty } \frac { c } { { { x ^ r } } } = 0$$

توجه کنید که دلیل اینکه پارامتر‌ $$r$$ باید مثبت باشد این است که اگر مقدار $$r$$ منفی باشد، عملا عبارت $${ x ^ r }$$ در مخرج قرار نگرفته است و به صورت کسر منتقل می‌شود. بنابراین پاسخ آن متفاوت خواهد بود.

در حالت دوم نیز اگر $$r = \frac { 1 } { 2 }$$ باشد، تابع $${ x ^ r }$$ برای xهای منفی تعریف نشده است. زیرا رادیکال یک عدد منفی، پاسخ حقیقی ندارد. بنابراین در صورت نکته یک محدودیت گذاشته شده است.

نکته مهم دیگری که باید به آن توجه کرد این است که علامت $$c$$، پاسخ مسئله را تحت تاثیر قرار نمی‌دهد و در نکات بالا، پاسخ برای مقادیر مثبت و منفی $$c$$، برابر با صفر خواهد بود. در ادامه با استفاده از یک مثال، شیوه محاسبه حد در بینهایت را مورد ارزیابی قرار می‌دهیم.

مثال 1

پاسخ حد زیر را به دست آورید.

$$\large \mathop { \lim } \limits _ { x \to \infty } \left ( { 2 { x ^ 4 } - { x ^ 2 } - 8 x } \right )$$

اولین ایده برای محاسبه حد بالا این است که مقدار بینهایت را به جای متغیر موجود در مسئله قرار دهیم و حاصل حد را محاسبه کنیم. اما زمانی که اینکار را انجام دهیم حاصل حد فوق به صورت زیر در می‌آید.

$$\large \mathop { \lim } \limits _ { x \to \infty } \left ( { 2 { x ^ 4 } - { x ^ 2 } - 8 x } \right ) = \infty - \infty - \infty$$

توجه کنید که محاسبه این مقدار، کار پیچیده‌ای است و این عبارت یک عبارت مبهم محسوب می‌شود. دلیل این موضوع این است که ممکن است مقدار عبارت بالا برابر با ∞ یا ∞- و یا صفر شود. در واقع حتما باید عمل دیگری انجام شود تا بتوان مقدار این حد را محاسبه کرد و بدون انجام محاسبات اضافی، محاسبه مقدار $$\infty - \infty$$ غیر ممکن است. در واقع برای رفع ابهام این عبارت باید با انواع مختلف بینهایت آشنایی داشته باشید.

بنابراین از تمام عبارات موجود در رابطه بالا، عبارت $${ x ^ 4 }$$ را فاکتور می‌گیریم (شیوه فاکتورگیری و تجزیه چند جمله‌ای‌ها در مطلب «اتحاد و تجزیه در ریاضی» وبلاگ فرادرس به صورت دقیق مورد بررسی قرار گرفته است). بنابراین داریم:

$$\large \mathop { \lim } \limits _ { x \to \infty } \left ( { 2 { x ^ 4 } - { x ^ 2 } - 8 x } \right ) = \mathop { \lim } \limits _ { x \to \infty } \left [ { { x ^ 4 } \left ( { 2 - \frac { 1 } { { { x ^ 2 } } } - \frac { 8 } { { { x ^ 3 } } } } \right ) } \right ]$$

شما می‌توانید با ضرب کردن عبارت $${ x ^ 4 }$$ در $$( 2 - \frac { 1 } { { { x ^ 2 } } } - \frac { 8 } { { { x ^ 3 } } } )$$، درستی فاکتورگیری فوق را مورد ارزیابی قرار دهید.

در ادامه حد هرکدام از عبارات فاکتورگیری شده را به صورت مجزا مورد محاسبه قرار می‌دهیم. این موضوع در رابطه زیر نشان داده شده است.

$$\large \mathop { \lim } \limits _ { x \to \infty } { x ^ 4 } = \infty \hspace { 0.25 in } \hspace { 0.25 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to \infty } \left ( { 2 - \frac { 1 } { { { x ^ 2 } } } - \frac { 8 } { { { x ^ 3 } } } } \right ) = 2$$

حد اول در رابطه فوق، به وضوح برابر با بینهایت می‌شود. اما برای محاسبه حد دوم از دو نکته‌ای که قبل از مثال بیان شد، استفاده کردیم. بنابراین حد در بینهایت مربوط به دو کسر موجود در رابطه سمت راست، برابر با صفر خواهد بود و حد کلی عبارت سمت راست برابر با عدد ۲ می‌شود.

برای محاسبه حد کلی عبارت صورت سوال، کافی است که از نکته بیان شده در ابتدای این مطلب استفاده کنیم. این نکته بیان می‌کند که حاصل ضرب بینهایت در یک عدد برابر با بینهایت می‌شود. بنابراین داریم:

$$\large \mathop { \lim } \limits _ { x \to \infty } \left ( { 2 { x ^ 4 } - { x ^ 2 } - 8 x } \right ) = \infty$$

بنابراین همانطور که مشاهده می‌شود، در این مثال حد مبهم $$\infty - \infty$$ را محاسبه کردیم و حاصل آن برابر با $$\infty$$ شد.

قانون دوم

در ادامه یک قانون ساده در مورد چند جمله‌ای‌ها مورد بررسی قرار می‌گیرد.

بر این اساس یک چند جمله‌ای درجه n را به شکل زیر در نظر بگیرید.

$$\large p \left ( x \right ) = { a _ n } { x ^ n } + { a _ { n - 1 } } { x ^ { n - 1 } } + \cdots + { a _ 1 } x + { a _ 0 }$$

توجه کنید که در این چند جمله‌ای رابطه $${ a _ n } \ne 0$$ برقرار است. بنابراین دو رابطه زیر را می‌توان برای حد در بینهایت مربوط به تابع فوق بیان کرد.

$$\large \mathop { \lim } \limits _ { x \to \infty } p \left ( x \right ) = \mathop { \lim } \limits _ { x \to \infty } { a _ n }{ x ^ n } \hspace { 0.25 in } \hspace { 0.25 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to - \infty } p \left ( x \right ) = \mathop { \lim } \limits _ { x \to - \infty } { a _ n } { x ^ n }$$

همانطور که در رابطه بالا نشان داده شده است، حد در بینهایت یک چند جمله‌ای برابر با حد بزرگترین درجه و توان آن چند جمله‌ای است. بنابراین در مثال‌های مختلف حد در بینهایت کافی است که بزرگترین توان آن چند جمله‌ای را جایگزین کل چند جمله‌ای کنیم.

این روابط را در قالب مثالی به صورت دقیق مورد بررسی قرار می‌دهیم.

مثال 2

حدهای نشان داده شده در رابطه زیر را محاسبه کنید.

$$\large \mathop { \lim } \limits _ { x \to \infty } \frac { { 2 { x ^ 4 } - { x ^ 2 } + 8 x } } { { - 5 { x ^ 4 } + 7 } } \hspace { 0.75 in } \mathop { \lim } \limits _ { x \to - \infty } \frac { { 2 { x ^ 4 } - { x ^ 2 } + 8 x } } { { - 5 { x ^ 4 } + 7 } }$$

توجه کنید که تنها تفاوت این دو عبارت این است که مقدار x در رابطه اول به سمت ∞ و در عبارت دوم به سمت ∞- میل می‌کند. این تفاوت در برخی از اوقات می‌تواند منجر به تفاوت در پاسخ نهایی مسئله شود. بنابراین در این مثال از ∞ شروع می‌کنیم.

همانطور که اشاره شد، مقدار نهایی عبارت موجود در صورت سوال، برابر است با قرار دادن ∞ در بزرگترین توان آن و مقدار نهایی مخرج نیز به شیوه مشابه محاسبه می‌شود. بنابراین داریم:

$$\large \mathop { \lim } \limits _ { x \to \infty } \frac { { 2 { x ^ 4 } - { x ^2 } + 8 x } } { { - 5 { x ^ 4 } + 7 } } = \frac { \infty } { { - \infty } }$$

همانطور که مشاهده می‌شود، این کسر تبدیل به یک بینهایت به روی بینهایت شده است. بنابراین یک کسر مبهم به حساب می‌آید و برای محاسبه آن باید از نکات ذکر شده در قوانین اول و دوم این مطلب استفاده کنیم.

با توجه به عبارت بالا متوجه می‌شویم که بزرگترین توان هر دو چند جمله‌ای صورت و مخرج در جمله $${ x ^ 4 }$$ مشاهده می‌شود. بر این اساس از عبارت $${ x ^ 4 }$$ موجود در صورت و مخرج فاکتور می‌گیریم. این موضوع در رابطه زیر نشان داده شده است.

$$\large \mathop { \lim } \limits _ { x \to \infty } \frac { { 2 { x ^ 4 } - { x ^ 2 } + 8 x } } { { - 5 { x ^ 4 } + 7 } } = \mathop { \lim } \limits _ { x \to \infty } \frac { { { x ^ 4 } \left ( { 2 - \frac { 1 } { { { x ^ 2 } } } + \frac { 8 } { { { x ^ 3 } } } } \right ) } }{ { { x ^ 4 } \left ( { - 5 + \frac { 7 } { { { x ^4 } } } } \right ) } }$$

با دقت به رابطه بالا متوجه می‌شویم که می‌توان عبارات $${ x ^ 4 }$$ را در صورت و مخرج با یکدیگر ساده کرد. بنابراین رابطه فوق به شکل زیر محاسبه می‌شود.

$$\large \begin {align*} \mathop { \lim } \limits _ { x \to \infty } \frac { { 2 { x ^ 4 } - { x ^ 2 } + 8 x } } { { - 5 { x ^ 4 } + 7 } } & = \mathop { \lim } \limits _ { x \to \infty } \frac { { 2 - \frac { 1 } { { { x ^ 2 } } } + \frac { 8 } { { { x ^ 3 } } } } } { { - 5 + \frac { 7 } { { { x ^ 4 } } } } } \end {align*}$$

در ادامه و برای محاسبه کسر بالا، مقدار ∞ را در صورت و مخرج جایگذاری می‌کنیم. با قرار دادن این مقدار، عبارات کسری موجود در رابطه بالا، مانند $${ 1 \over { x ^ 2 } }$$ برابر با صفر می‌شوند. بنابراین رابطه فوق به شکل ساده شده زیر در می‌آید.

$$\large \begin {align*} \mathop { \lim } \limits _ { x \to \infty } \frac { { 2 - \frac { 1 } { { { x ^ 2 } } } + \frac { 8 } { { { x ^ 3 } } } } } { { - 5 + \frac { 7 } { { { x ^ 4 } } } } } & = \frac { { 2 + 0 + 0 } } { { - 5 + 0 } } \\ & = - \frac { 2 } { 5 } \end {align*}$$

بنابراین رفع ابهام صورت گرفت و حد در بینهایت، زمانی که x به سمت ∞ میل می‌کند، محاسبه شد. در ادامه و برای به دست آوردن حد دوم یعنی زمانی که x به سمت ∞- میل می‌کند، روند مشابهی را طی می‌کنیم و این موضوع در رابطه زیر به خوبی نشان داده شده است.

$$\large \mathop { \lim } \limits _ { x \to - \infty } \frac { { 2 { x ^ 4 } - { x ^ 2 } + 8 x } } { { - 5 { x ^ 4 } + 7 } } = - \frac { 2 } { 5 }$$

همانطور که در مثال بالا مشاهده شد، تغییر دادن ∞ به ∞-، پاسخ نهایی مسئله را عوض نکرد. اما در تمام مسائل این چنین نیست و ممکن است در یک مسئله حد در بینهایت با تغییر ∞ به ∞-، پاسخ مسئله به کلی تغییر کند. این موضوع در مثال زیر به خوبی مورد بررسی قرار گرفته است.

مثال ۳

حدود زیر را محاسبه کنید.

$$\large \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } }{ { 5 - 2 x } } \hspace { 0.75 in } \mathop { \lim } \limits _ { x \to - \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } } { { 5 - 2 x } }$$

حضور رادیکال در عبارات بالا، تغییری در روند کلی انجام محاسبات ایجاد نمی‌کند ولی اندکی محاسبه حد را پیچیده می‌کند.

با قرار دادن مقدار ∞ در رابطه فوق، متوجه می‌شویم که حاصل کسر فوق نیز مانند مثال قبل، به صورت یک عبارات بینهایت به روی بینهایت در می‌آید و برای رفع ابهام آن (در صورت امکان) باید از صورت و مخرج کسر فاکتور بگیریم. این موضوع در رابطه زیر نشان داده شده است.

$$\large \begin {align*} \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } } { { 5 - 2 x } } & = \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { { x ^ 2 } \left ( { 3 + \frac { 6 } { { { x ^ 2 } } } } \right ) } } } { { x \left ( { \frac { 5 } { x } - 2 } \right ) } } \\ & = \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { { x ^ 2 } } \sqrt { 3 + \frac { 6 } { { { x ^ 2 } } } } } } { { x \left ( { \frac { 5 } { x } - 2 } \right ) } } \end {align*}$$

اما برای محاسبه رادیکال نشان داده شده، یعنی $$\sqrt { { x ^ 2 } }$$ باید دقت بسیار زیادی بکنیم. این موضوع در رابطه زیر نشان داده شده است.

$$\large { \sqrt { { x ^ 2 } } = \left | x \right | }$$

همانطور که مشاهده می‌شود، برای محاسبه عبارت فوق به قدر مطلق نیاز داریم. دلیل این موضوع این است که ریشه دوم یک عدد، حتما باید برابر با عددی مثبت باشد. بنابراین رابطه فوق به شکل ساده شده زیر در می‌آید.

$$\large { \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } }{ { 5 - 2 x } } = \mathop { \lim } \limits _ { x \to \infty } \frac { { \left | x \right | \sqrt { 3 + \frac { 6 } { { { x ^ 2 } } } } } } { { x \left ( { \frac { 5 } { x } - 2 } \right ) } } }$$

در مطلب «قدر مطلق — به زبان ساده» وبلاگ فرادرس به خوبی اشاره شد که قدر مطلق عبارت x زمانی که x مقداری مثبت داشته باشد برابر با x و زمانی که x منفی باشد برابر با x- است. این مفهوم در رابطه زیر به خوبی نشان داده شده است.

$$ \large { \left | x \right | = \left\{ { \begin {array} { rl } x & { { \mbox{if } } x \ge 0 } \\ { - x } & { { \mbox { if } } x < 0 } \end {array} }\right . } $$

بنابراین با توجه به رابطه فوق، پاسخ نهایی حد نشان داده شده زمانی که x به سمت ∞ و یا ∞- میل می‌کند، متفاوت خواهد بود.

بر این اساس ابتدا حد نشان داده شده در صورت سوال را زمانی که x به سمت ∞ میل می‌کند، محاسبه می‌کنیم. در این حالات مقدار $$\left | x \right |$$ برابر با $${ x }$$ خواهد بود. در نتیجه داریم:

$$\large { \begin {align*} \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } } { { 5 - 2 x } } & = \mathop { \lim } \limits _ { x \to \infty } \frac { { x \sqrt { 3 + \frac { 6 } { { { x ^ 2 } } } } } } { { x \left ( { \frac { 5 } { x } - 2 } \right ) } } \\ & = \mathop { \lim } \limits _ { x \to \infty } \frac { { \sqrt { 3 + \frac { 6 } { { { x ^ 2 } } } } } } { { \frac { 5 } { x } - 2 } } = \frac { { \sqrt { 3 + 0 } } } { { 0 - 2 } } = - \frac { { \sqrt 3 } } { 2 } \end {align*} }$$

بنابراین حد اول با توجه به روند توضیح داده شده، محاسبه شد. در ادامه به محاسبه حد دوم یعنی حالتی که x به سمت ∞- میل می‌کند، می‌پردازیم. بنابراین رابطه حد را به شکل زیر بازنویسی می‌کنیم.

$$\large { \mathop { \lim } \limits _ { x \to - \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } } { { 5 - 2 x } } = \mathop { \lim } \limits _ { x \to - \infty } \frac { { \left | x \right | \sqrt { 3 + \frac { 6 } { { { x ^ 2 } } } } } } { { x \left ( { \frac { 5 } { x } - 2 } \right ) } } }$$

در ادامه با توجه به تعریف قدر مطلق، رابطه فوق را می‌توان به شکل زیر بیان کرد.

$$\large { \begin {align*} \mathop { \lim } \limits _ { x \to - \infty } \frac { { \sqrt { 3 { x ^ 2 } + 6 } } } { { 5 - 2 x } } & = \mathop { \lim } \limits _ { x \to - \infty } \frac { { - x \sqrt { 3 + \frac { 6 } { { { x ^ 2 } } } } } } { { x \left ( { \frac { 5 } { x } - 2 } \right ) } } \\ & = \mathop { \lim } \limits _ { x \to - \infty } \frac { { - \sqrt { 3 + \frac { 6 }{ { { x ^ 2 } } } } } } { { \frac { 5 } { x } - 2 } } \\ & = \frac { { \sqrt 3 } } { 2 } \end {align*} }$$

بنابراین همانطور که در این مثال مشاهده شد، حد رابطه داده شده در صورت سوال، زمانی که x به سمت ∞ میل می‌کند برابر با $$- { \frac { { \sqrt 3 } } { 2} }$$ و زمانی که x به سمت ∞- میل می‌کند، برابر با $${ \frac { { \sqrt 3 } } { 2} }$$ است.

در این مثال، تغییر علامت بینهایت (∞ به ∞-) تنها علامت پاسخ نهایی را تغییر داد ولی در برخی دیگر از حالات، ممکن است که پاسخ حد به صورت کامل تغییر کند.

مجانب افقی

در مبحث حد بینهایت اشاره شد که پاسخ حد بینهایت برابر با مجانب قائم تابع است. اما نوع دیگری از مجانب نیز وجود دارد که به مجانب افقی معروف است و برای محاسبه آن از نکات موجود در مبحث حد در بینهایت استفاده می‌کنیم.

در واقع زمانی که حد یک تابع را در بینهایت (حد در بینهایت یک تابع) محاسبه می‌کنیم، مجانب افقی آن تابع به دست آمده است.

این موضوع را می‌توان به خوبی با استفاده از رابطه زیر نمایش داد.

$${ \mathop { \lim } \limits _ { x \to \infty } f \left ( x \right ) = L \hspace { 0.25 in } \hspace { 0.25 in } \hspace { 0.25 in } \mathop { \lim } \limits _ { x \to - \infty } f \left ( x \right ) = L }$$

همانطور که اشاره شد، مجانب افقی، مقدار یک تابع در بینهایت را نشان می‌دهد. شکل زیر مجانب قائم و افقی یک تابع را با استفاده از نمودار آن تابع به تصویر کشیده است.

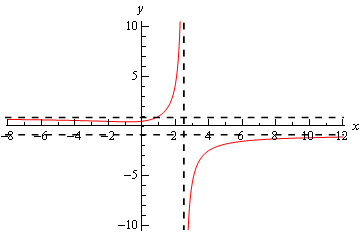
در ادامه یکی دیگر از مثال‌ها در زمینه حد در بینهایت را مورد مطالعه قرار می‌دهیم.

مثال ۴

حدود زیر را با استفاده از مفاهیم و روابط حد در بینهایت محاسبه کنید.

$$\large \mathop { \lim } \limits _ { z \to \infty } \frac { { 4 { z ^ 2 } + { z ^ 6 } } } { { 1 - 5 { z ^ 3 } } } \hspace { 0.75 in } \mathop { \lim } \limits _ { z \to - \infty } \frac { { 4 { z ^ 2 } + { z ^ 6 } } } { { 1 - 5 { z ^ 3 } } }$$

با قرار دادن مقدار ∞ در صورت کسر داده شده، مقدار صورت برابر با بینهایت می‌شود. همچنین اگر مقدار ∞ را در مخرج کسر قرار دهیم، مقدار آن برابر با ∞- می‌شود. بنابراین با یک کسر بینهایت به روی بینهایت روبه‌رو هستیم و برای محاسبه آن باید با استفاده از فاکتورگیری، رفع ابهام را انجام دهیم.

بر این اساس، از عبارت $${ z ^ 3 }$$ در صورت و مخرج فاکتور می‌گیریم. این موضوع در رابطه زیر نشان داده شده است.

$$\large \begin {align*} \mathop { \lim } \limits _ { z \to \infty } \frac { { 4 { z ^ 2 } + { z ^ 6 } } } { { 1 - 5 { z ^ 3 } } } & = \mathop { \lim } \limits _ { z \to \infty } \frac { { { z ^ 3 } \left ( { \frac { 4 } { z } + { z ^ 3 } } \right ) } } { { { z ^ 3 } \left ( { \frac { 1 } { { { z ^ 3 } } } - 5 } \right ) } } \\ & = \mathop { \lim } \limits _ { z \to \infty } \frac { { \frac { 4 } { z } + { z ^ 3 } } } { { \frac { 1 } { { { z ^ 3 } } } - 5 } } \end {align*}$$

در ادامه و با قرار دادن مقدار ∞ در کسر فوق، عبارت اول موجود در صورت و مخرج برابر با صفر خواهند شد. در نتیجه، مخرج کسر فوق برابر با 5- و صورت این کسر برابر با ∞ ($${ z ^ 3 }$$) خواهد بود. در نهایت رابطه فوق به شکل زیر در می‌آید.

$$\large \mathop { \lim } \limits _ { z \to \infty } \frac { { 4 { z ^ 2 } + { z ^ 6 } } } { { 1 - 5 { z ^ 3 } } } = \frac { \infty } { { - 5 } } = - \infty$$

برای محاسبه مقدار حد صورت سوال در ∞-، روندی مشابه بالا را طی می‌کنیم، این موضوع در رابطه زیر نشان داده شده است.

$$\large \mathop { \lim } \limits _ { z \to - \infty } \frac { { 4 { z ^ 2 } + { z ^ 6 } } }{ { 1 - 5 { z ^ 3 } } } = \mathop { \lim } \limits _ { z \to - \infty } \frac { { \frac { 4 } { z } + { z ^ 3 } } } { { \frac { 1 } { { { z ^ 3 } } } - 5 } } = \frac { { - \infty } } { { - 5 } } = \infty$$

بنابراین همانطور که مشاهده می‌شود، حد در بینهایت کسر داده شده زمانی که x به سمت ∞ میل می‌کند برابر با ∞- و زمانی که متغیر x به سمت ∞- میل می‌کند برابر با ∞ خواهد بود.