جذر تقریبی و روش محاسبه آن – آموزش به زبان ساده و با مثال

حل معادلات و پیدا کردن ریشه اعداد در ریاضی از اهمیت زیادی برخوردار است. ولی در اکثر مواقع، یپدا کردن ریشه یا جذر اعداد به راحتی امکان‌پذیر نیست زیرا نمی‌توان آن‌ها را به صورت مربع کامل درآورد. در این وضعیت معمولا به سراغ جذر تقریبی و روش محاسبه آن می‌رویم و به کمک تکنیک‌هایی، مقداری تقریبی برای جذر یک عدد پیدا می‌کنیم. این نوشتار از مجله فرادرس، مربوط به روش‌هایی است که به کمک آن‌ها قادریم، برای یک عدد، به صورت تقریبی، جذر را محاسبه کرده و با تعداد ارقام اعشار مناسب، نتیجه را گزارش کنیم.

اگر می‌خواهید با جذر و ریشه یابی با تکنیک‌های هندسی و تکراری آشنا شوید، نوشتارهای اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده و  جذر یا محاسبه ریشه دوم عدد — به زبان ساده  از مجله فرادرس را مطالعه کنید. همچنین خواندن مطالب معادله رادیکالی — به زبان ساده و قضیه فیثاغورس و کاربردهای آن — به زبان ساده نیز خالی از لطف نیست.

جذر تقریبی و روش محاسبه آن

در بعضی مواقع، هنگامی که در هندسه با قضیه فیثاغورس مواجه هستید یا در هنگامی که به حل یک معادله درجه دو مشغولید، باید بتوانید ریشه دوم یا جدر یک عدد را بدست آورید. متاسفانه همه اعداد به صورت مربع کامل نیستند و مقدار ریشه یا جذر آن‌ها، مقداری از اعداد طبیعی نیست. در این حالت باید به کمک تکنیک‌هایی، مقدار تقریبی و اعشاری ریشه اعداد را بدست آوریم. اگر ماشین حساب در دسترس باشد، می‌توانیم چنین کاری را انجام دهیم ولی اگر هیچ ماشین حساب یا یک گوشی هوشمندی در اختیارمان نباشد، امکان بدست آوردن مقدار جذر تقریبی، بدون خواندن این مطلب، میسر نخواهد بود.

در این نوشتار به کمک یک مداد و کاغذ (به شکل سنتی) و با تکرار بعضی از مراحل، جذر تقریبی و روش محاسبه آن را به شما آموزش خواهیم داد. به این منظور، دو راهکار ارائه می‌دهیم که در اولین روش، مقدار تقریبی را با «حدس، مقایسه و تقسیم» محاسبه کرده و در روش دوم که همان روشی مرحله به مرحله است، با طی کردن گام‌های تکراری به ریشه تقریبی اعداد خواهیم رسید.

روش اول، حدس، مقایسه و تقسیم

با محاسبه جذر یا رادیکال در ریاضیات پایه‌های مختلف سر و کار داریم، اما روش جذر تقریبی هشتم از دو عدد صحیح قبل و بعد از عدد مورد نظر کمک می‌گیرد. یعنی ابتدا با دو حدس اولیه برای مقدار تقریبی ریشه یا جذر عدد آغاز کرده و با تکرار مراحلی، مقدار تقریبی جذر، بدست می‌آید. در ادامه به معرفی این مدل از محاسبه ریشه دوم اعداد خواهیم پرداخت. این محاسبات بخصوص زمانی که به ریشه معادلات رادیکالی می‌رسید، بسیار اهمیت پیدا می‌کند.

جذر تقریبی تا یک رقم اعشار

در اینجا ، فرض بر این است که می‌خواهیم ریشه دوم یک عدد صحیح را بدست آوریم. مراحل اجرای این کار را با ذکر یک مثال ساده آغاز کرده و با مثال‌های دیگر دنبال و آموزش می‌دهیم. در نوشتاری دیگر به بررسی جذر اعداد حقیقی یا اعشاری نیز خواهیم پرداخت.

مثال ۱

فرض کنید به دنبال ریشه دوم یا جذر تقریبی عدد ۵۵ هستیم. می‌دانیم که ۵۵ یک عدد مربع کامل نیست. به دنبال دو عدد می‌گردیم که به ۵۵ نزدیک بوده و از طرفی عددی باشند که به صورت مربع کامل نوشته می‌شوند. واضح است که ۵۵ بین اعداد 49 و 64 که هر دو مربع کامل هستند، قرار گرفته. پس به عنوان حدس اولیه می‌دانیم که ریشه دوم ۵۵ بین دو عدد ۷ و ۸ قرار دارد.

$$\large {\displaystyle 4 9 < 5 5 < 6 4 }$$

$$\large {\displaystyle \sqrt{ 7} < \sqrt{ 5 5} < \sqrt{ 8} }$$

$$\large {\displaystyle 7 < \sqrt{5 5} < 8 }$$

نکته: مقدار تقریبی ریشه دوم عدد ۵۵ به کمک ماشین حساب، عدد 7٫416 است.

فیلم آموزش محاسبات سریع ریاضی – به زبان ساده + گواهینامه در فرادرس

کلیک کنید

با تعیین این حدود، مراحل زیر را طی می‌کنیم تا با دقت یک رقم اعشار به مقدار جذر تقریبی ۵۵ برسیم.

• عدد وسط دو عدد صحیح (در اینجا 7و 8) که در دوکران بالا و پایین نامساوی‌های بالا قرار دارند را مشخص کنید. حاصل برای مثال ما برابر با $$\dfrac{ 8 + 7}{2} = 7.5$$ است.
• عدد حاصل را به توان ۲ می‌رسانیم. پس خواهیم داشت $$7.5^2 = 56.25$$.
• اگر مجذور عدد بدست آمده (56٫25)، بزرگتر از عددی است که می‌خواهیم جذر آن را محاسبه کنیم، باید اعداد بین کران پایین و ۷٫۵ را برای پیدا کردن مقدار جذر تقریبی مورد بررسی قرار دهیم.
• اگر مجذور عدد بدست آمده، کوچکتر از عددی است که می‌خواهیم جذر آن را بدست آوریم، به سراغ اعداد بین کران بالا و ۷٫۵ خواهیم رفت.
• با توجه به دو بند قبلی، به کران پایین، به میزان ۰٫۱ اضافه کرده و چهار عدد ۷٫۱، ۷٫۲، ۷٫۳ و ۷٫۴ را در نظر می‌گیریم. (در صورت بزرگتر بودن عدد مورد نظر از مجذور بدست آمده، از اعداد ۷٫۶، ۷٫۷، ۷٫۸ و ۷٫۹ استفاده می‌کردیم).
• هر یک از اعداد با افزایش ۰٫۱ را به صورت مربع کامل درآورده و با مقدار ۵۵ مقایسه می‌کنیم.
• نزدیک‌ترین عدد حاصل، ریشه دوم عدد ۵۵ با یک رقم اعشار خواهد بود.

به توجه به مثال ما، جدول زیر می‌تواند راهکار ارائه شده را به شکل مناسب‌تری نشان دهد.

در سطر سوم از جدول بالا، قدر مطلق فاصله ۵۵ از عدد مربوط به سطر دوم محاسبه شده. از آنجایی که ۵۴٫۷۶ کمترین فاصله را با ۵۵ دارد، می‌توان ریشه دوم ۵۵ را به صورت تقریبی برابر با جذر آن یعنی ۷٫۴ گرفت. پس ریشه دوم ۵۵ با یک رقم اعشار برابر است با ۷٫۴.

مثال ۲

این بار عدد مورد نظر را ۶۲ در نظر می‌گیریم که می‌دانیم ریشه دوم هم ندارد. از طرفی مشخص است که ۶۲ به ۶۴ نزدیک تر بوده، پس باید ریشه دوم ۶۲ به عدد ۸ نزدیکتر باشد. ولی به هر حال روال گفته شده در قبل را طی خواهیم کرد. نامساوی‌های قبلی را دوباره تکرار می‌کنیم.

$$\large {\displaystyle 4 9 < 6 2 < 6 4 }$$

$$\large {\displaystyle \sqrt{ 7} < \sqrt{ 6 2 } < \sqrt{ 8} }$$

$$\large {\displaystyle 7 < \sqrt{6 2} < 8 }$$

• مشخص است که باز هم عدد وسط دو عدد صحیح (در اینجا 7و 8) برای پیدا کردن پیدا کردن مقدار تقریبی لازم است. $$\dfrac{ 8 + 7}{2} = 7.5$$ است.
• مجذور یا مربع ۷٫۵ برابر است با ۵۶٫۲۵ که کوچکتر از عدد مورد نظر ما یعنی ۶۲ است. پس اعداد بزرگتر از ۷٫۵ را در نظر گرفته و با افزایش و گام‌هایی با مقدار ۰٫۱، ۴ عدد بعدی تا ۸ را محاسبه می‌کنیم.
• نتیجه به مانند جدول تصویر پایین خواهد بود. ولی این بار به چهار عدد انتهایی این جدول توجه می‌کنیم.

• کمترین مقدار در سطر سوم جدول بالا، برابر است با 0٫۴۱ که نشانگر جذر تقریبی ۶۲ است. عدد مورد نظر در سطر اول برای این ستون، ۷٫۹ بوده که مقدار تقریبی ریشه دوم ۶۲ را نشان می‌دهد.

همانطور که دیدید، با طی کردن چند مرحله و اجرای محاسباتی ساده، جذر تقریبی یک عدد صحیح را بدست آوردیم. در قسمت بعدی، به کمک روشی مشابه، جذر تقریبی تا دو رقم اعشار را به کار خواهیم گرفت.

نکته: مقدار تقریبی ریشه دوم عدد 62 به کمک ماشین حساب، عدد 7٫784 است.

فیلم مجموعه آموزش مفاهیم پایه ریاضی و هندسه – به زبان ساده در فرادرس

کلیک کنید

جذر تقریبی تا دو رقم اعشار

اگر مقدار تقریبی جذر یک عدد تا یک رقم اعشار را به دست آورده‌اید، می‌توانید، با تکرار مراحل گفته شده در قسمت قبل، دقت محاسباتتان را افزایش دهید. باز هم مثال‌های قبلی را مورد استقاده قرار داده و جذر تقریبی دو عدد ۵۵ و ۶۲ را تا دو رقم اعشار پی‌ می‌گیریم.

مثال ۳

با توجه به مثال ۱، می‌دانیم که جذر تقریبی ۵۵ در بازه ۷٫۴ تا ۷٫۵ قرار دارد. این بار این دو عدد را به عنوان کران‌های پایین و بالا در نظر گرفته و عملیات قبلی را تکرار می‌کنیم. فقط توجه داشته باشید که میزان افزایش در اینجا به جای ۰٫۱، عدد ۰٫۰۱ خواهد بود.

$$\large {\displaystyle 5 4 . 7 6 < 5 5 < 5 6 . 2 5 }$$

$$\large {\displaystyle \sqrt{ 5 4 . 76} < \sqrt{ 5 5} < \sqrt{ 5 6 . 25 } }$$

$$\large {\displaystyle 7. 4 < \sqrt{5 5} < 7 . 5 }$$

حال وسط دو عدد ۷٫۵ و ۷٫۴ را بدست آورده و آن را مجذور می‌کنیم.

$$\large {\displaystyle \dfrac{ 7.4 + 7.5 } { 2} = 7. 45 }$$

$$\large {\displaystyle (7. 45) ^2 = 55 . 50 25 }$$

در ادامه عملیات پیدا کردن ریشه دوم به شکل تقریبی، جدولی مانند جدول بالا را ایجاد می‌کنیم. از انجایی که کمترین اختلاف با ۵۵ برای عدد ۷٫۴۲ حاصل شده، جذر تقریبی ۵۵ با دو رقم اعشار همان عدد خواهد بود.

نکته: توجه دارید که چون مربع کامل ۷٫۴۵ که برابر با ۵۵٫۵۰ است، بزرگتر از ۵۵ است، باید به چهار عدد کوچکتر در جدول بالا توجه کنیم، اعداد بعدی فقط به جهت مقایسه نوشته شده‌اند.

مثال ۴

باز هم به سراغ عدد ۶۲ می‌رویم و این بار با دو رقم اعشار، ریشه دوم یا جذر تقریبی آن را محاسبه می‌کنیم. از قسمت قبل می‌دانیم که ریشه دوم ۶۲ با یک رقم اعشار در بین دو عدد 7٫۸ تا ۷٫۹ است. بنابراین این ناحیه را مورد جستجو قرار می‌دهیم.

مقدار وسط این دو عدد برابر است با ۷٫۸۵. مجذور یا مربع ۷٫۸۵ نیز برابر است با ۶۱٫۶۲ که چون از ۶۲ کوچکتر است، از بین چهار عدد بعد از ۷٫۹ با افزایش ۰٫۰۱، به دنبال ریشه دوم یا جذر تقریبی ۶۲ می‌گردیم. به این منظور جدول زیر را تهیه کرده‌ایم.

با مقایسه قدرمطلق فاصله مربعات اعداد با ۶۲، مشخص می‌شود که کمترین فاصله برابر با ۰٫۰۶۳۱ بوده که مربوط به ۷٫۸۷ است. بنابراین ریشه دوم ۶۲ با دو رقم اعشار، برابر با ۷٫۸۷ است.

نکته: می‌توانیم همین کار را تکرار کرده و به تقریب‌های بیشتری برای پیدا کردن ریشه دوم اعداد برسیم. هر چه تعداد تکرارها را بیشتر کنیم، عدد دقیق‌تری بدست خواهد آمد.

ناگفته نماند که روش به کار رفته برای پیدا کردن ریشه دوم عدد، برگرفته از تکنیک ریشه‌یابی معادله درجه دو به کمک الگوریتم نیوتن رافسون است.

روش دوم، جذر تقریبی با ریشه یابی

به غیر از روش مربوطه که در قسمت قبل معرفی کردیم، یک تکنیک دیگر نیز وجود دارد که به کمک آن ریشه یا جذر تقریبی اعداد را بدست می‌آوریم. البته شاید از جنبه‌ای، این تکنیک نیز به مانند قبل عمل کند، ولی نحوه نوشتن و اجرای آن متفاوت است. خواهید دید که این راهکار مشابه ایجاد دو جمله‌ای درجه دوم و اتحاد مربع کامل است. در ادامه به ذکر چند مثال برای روشن شدن موضوع جذر تقریبی یا ریشه یابی خواهیم پرداخت.

مثال ۵

فرض کنید قرار است ریشه دوم عدد ۲۰۲۵ را بدست آوریم. برای شروع، فضای کار را برای محاسبه جذر تقریبی این عدد آماده می‌کنیم.

سه ناحیه را روی کاغذ ترسیم به مانند شکل زیر ایجاد می‌کنیم. البته این ناحیه‌ها، خیلی شبیه تقسیم عدد صحیح هستند ولی از آن برای ریشه‌یابی استفاده خواهیم کرد.

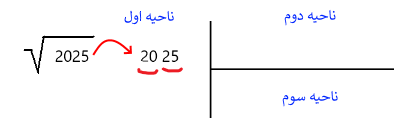
همانطور که مشاهده می‌کنید، در ناحیه اول، عددی که به جستجوی ریشه دوم آن هستیم را قرار داده‌ایم. در ناحیه دوم، مقدار ریشه دوم حاصل می‌شود و ناحیه سوم نیز برای عملیات کمکی لازم است.

گام اول در محاسبه جذر تقریبی: جداسازی دو رقم از راست

در گام اول، عدد مورد نظر را در ناحیه اول قرار داده و بدون علامت رادیکال نمایش می‌دهیم. این عدد یعنی ۲۰۲۵ را دو رقم دو رقم از سمت راست جدا می‌کنیم. حاصل به شکل ۲۵ ۲۰ در ناحیه اول قرار می‌گیرد. اگر عدد سه رقمی بود، یک بخش دو رقمی در سمت راست ایجاد می‌شد و یک رقم هم در سمت چپ. اگر عدد شش رقم داشت، به سه دسته دو رقمی تفکیک می‌شد.

برای مثال اگر با عدد 746917 سروکار داشتیم، آن را به صورت 17، 69، 74 نوشته و عملیات را اجرا می‌کردیم. همچنین برای پیدا کردن جذر تقریبی 19036 نیز جداسازی به صورت 36، 90، 1 صورت می‌گرفت. برای حل مثال گفته شده، بهتر است به تصویر بالا که مربوط به گام اول است، توجه کنید.

گام دوم در محاسبه جذر تقریبی: پیدا کردن نزدیکترین مربع کامل

به عنوان مرحله بعدی، باید بزرگترین عدد صحیح را به شکل پیدا کنیم که مربع کامل آن نزدیکترین مقدار به قسمت تفکیک شده سمت چپ باشد. توجه داشته باشید که این مربع این عدد باید از مقدار ۲۵ کوچکتر یا مساوی باشد. در اینجا ۱۶ عدد مربع است که نزدیکترین عدد به ۲۰ است. ۴ را در ناحیه دوم نوشته و مربع آن را در زیر ۲۰ و در ناحیه اول می‌نویسیم.

توجه دارید که دو عدد مربع کامل وجود دارد که به ۲۰ نزدیک هستند. این دو عدد ۱۶ و ۲۵ هستند. البته هر دو آن‌ها می‌توانند مناسب باشند، ولی همانطور که گفتیم،  در این گام، نزدیک‌ترین عددی انتخاب می‌شود که از ۲۰ کوچکتر باشد. به همین جهت از ریشه دوم ۱۶ یعنی ۴ استفاده کرده‌ایم.

گام سوم در محاسبه جذر تقریبی: محاسبه تفاضل

در این گام، مربع عدد بدست آمده در ناحیه دوم (یعنی ۱۶) را در زیر عدد مربوط به گام دوم نوشته و از آن کم می‌کنیم. یعنی ۱۶ را از ۲۰ کسر کرده و حاصل تفریق را با یک خط افقی از قسمت بالایی جدا می‌سازیم. این کار درست به مانند تقسیم عدد صحیح است. در مثال ما، حاصل این تفاضل ۴ است. در تصویر زیر نتیجه اجرای گام دوم و سوم را مشاهده می‌کنید.

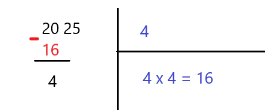
گام چهارم در محاسبه جذر تقریبی: اضافه کردن ارقام بعدی

در این مرحله، عدد مربوط به ناحیه دوم را در ۲ ضرب می‌کنیم و مقدار آن را در ناحیه سوم می‌نویسیم. برای مثال ما این عدد برابر است با ۸. همچنین در قسمت یا ناحیه سوم نیز عدد حاصل را به همراه یک فضای خالی برای رقم بعدی نوشته و به صورت ضرب در رقم نامعلوم وارد می‌کنیم. به منظور روشن شدن موضوع بهتر است به تصویر زیر توجه کنید.

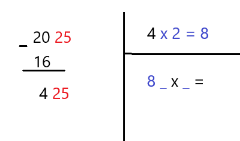
مشخص است که در ناحیه سوم، عبارت $$8 \_ x\_ =$$ به منظور تعیین عددی است که مربع کامل آن به ۲۰۲۵ نزدیک است. در مرحله بعد، باید مشخص می‌کنیم که چه رقمی در جای خالی رابطه بالا قرار گیرد. این کار در گام پنجم صورت خواهد گرفت.

گام پنجم در محاسبه جذر تقریبی: پیدا کردن بهترین گزینه برای جای خالی

در این مرحله، باید دو جای خالی در گام قبلی را تکمیل کنیم. ولی توجه داشته باشید که هر چند دو مکان برای رقم جدید نوشته شده ولی باید هر دو آن‌ها برابر باشند. این رقم را به شکلی استفاده می‌کنیم که ضرب آن در عدد حاصل از کنار هم گذاشتن رقم ۸ با رقم گفته شده، به ۴۲۵ نزدیک باشد.

فیلم مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست در فرادرس

کلیک کنید

برای مثال رقم ۶ را به کار می‌بریم. بنابراین فضاهای خالی را با ۶ پر کرده و حاصل ضرب به صورت $$86 \times 6$$ نوشته می‌شود. این حاصل‌ضرب برابر است با ۵۱۶ که فاصله زیادی با ۴۲۵ دارد. این بار یک رقم کمتر یعنی ۵ را امتحان می‌کنیم. در نتیجه حاصل ضرب با پرکردن جای خالی با رقم ۵ به شکل $$85 \times 5$$ نوشته شده که حاصلی برابر با ۴۲۵ دارد. دقیقا مقدار مورد نظرمان با عدد ظاهر شده در ناحیه اول، برابر است. پس به نتیجه مناسب یا رقم مناسب برای پیدا کردن ریشه دوم به صورت تقریبی رسیده‌ایم.

گام ششم در محاسبه جذر تقریبی: تفاضل صفر و پایان عملیات

رقم ۵ که در گام قبلی حاصل شد را در کنار رقم ۴ در گام دوم قرار می‌دهیم. عدد حاصل ۴۵ است. این عدد را به صورت مربع کامل درآورده و از آخرین عدد مربوط به ناحیه اول، کم می‌کنیم. اگر حاصل تفریق، صفر باشد، عملیات خاتمه یافته و در غیر اینصورت، دو رقم بعدی را از بالا به پایین آورده و گام‌های چهارم، پنجم و ششم را دوباره تکرار می‌کنیم تا به دقت مناسب برای پیدا کردن جذر تقریبی عدد مورد نظرمان برسیم.

با توجه به تصویر زیر، باقی‌مانده تفاضل مربوطه، صفر است پس ۴۵ را ریشه دوم ۲۰۲۵ بدست می‌آوریم.

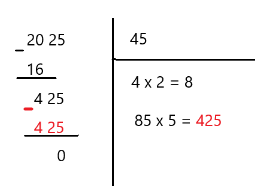
مثال ۶

این بار به ریشه دوم عدد ۲۵۱۶ می‌پردازیم. توجه داشته باشید که نتیجه جذر را تا دو رقم اعشار احتیاج داریم. البته شاید فکر کنید چون، با تفکیک دو رقم از راست به مقادیر ۱۶ و ۲۵ می‌رسیم، ریشه دوم برابر با ۵۴ باشد. ولی اگر مقدار ۵۴ را در خودش ضرب کنیم، حاصل برابر با 2916 خواهد بود که با مقدار مورد نظر ما اختلاف دارد. در نتیجه با طی کردن روال گفته شده در مثال‌های قبل، مراحل را طی کرده و به مقدار تقریبی ریشه دوم ۲۵۱۶ خواهیم رسید. فقط در این مثال، همه مراحل را در یک تصویر نمایش خواهیم داد ولی به منظور مشخص شدن بهتر این گام‌ها، آن‌ها را به رنگ‌های مختلف نشان خواهیم داد.

همانطور که می‌بینید، زمانی که رقمی برای اضافه کردن وجود ندارد، دو رقم صفر به سمت راست عدد (مثلا در گام آبی رنگ) اضافه کرده و یک ممیز نیز در ناحیه دوم برای نتیجه جذر، در نظر می‌گیریم. البته مراحل محاسبه تقریبی جذر در این مثال، باز هم می‌تواند ادامه داشته باشد ولی چون به دو رقم اعشار رسیده‌ایم، دیگر مراحل را تکرار نخواهیم کرد.

نکته: اگر ریشه دوم عدد ۲۵۱۶ را به کمک ماشین حساب بدست آورید، به مقدار 50٫15974482 خواهیم رسید که تا دو رقم اعشار با عدد حاصل از محاسبات ما، مطابقت دارد.

در متن دیگری از مجله فرادرس به پیدا کردن ریشه دوم اعداد اعشاری خواهیم پرداخت و به کمک مثالی، نحوه اجرای عملیات را با توجه به مراحل گفته شده در این متن، مرور خواهیم کرد.

خلاصه و جمع بندی

در آموزش جذر تقریبی در مجله فرادرس با یادآوری مفهوم جذر یا ریشه دوم و روش استفاده از ماشین‌حساب کلیات بحث را یاد گرفتیم و سپس روشی مفید و البته سریع برای محاسبه جذر تقریبی یک عدد را به کار بردیم. با این روش توانستیم عددهای رادیکالی را با دیگر اعداد مقایسه کنیم و همچنین محل تقریبی آن را بر روی محور اعداد نمایش دهیم؛ البته در درس‌نامه نمایش عدد رادیکالی روی محور روش نمایش دقیق عدد رادیکالی بر روی محور آموزش داده شده است. البته در پایه‌های بالاتر باز هم با ریشه‌گیری سر و کار خواهیم داشت.

دانشجویان رشته فنی مهندسی و علوم نیز باید محاسبه رادیکال را به یاد داشته باشند، هر چند در این مقطع، کمتر به مقدار تقریبی آن احتیاج است ولی آگاهی از نحوه محاسبه آن، به درک بهتر نتایج بدست آمده کمک خواهد کرد. به همین جهت نوشتاری‌های متعددی را به موضوع ریشه دوم یا جذر اعداد اختصاص داده‌ایم تا ضعفی که در بین دانش‌آموزان برای محاسبه جذر وجود دارد، از بین برود. در نوشتارهای بعدی، در مورد نحوه بدست آوردن ریشه دوم اعداد اعشاری بیشتر صحبت کرده و نحوه محاسبه آن را فراخواهیم گرفت.