توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

در نظریه آمار و احتمال، توزیع نرمال (Normal Distribution) یکی از مهم‌ترین توزیع‌های آماری است. البته به این توزیع گاهی «توزیع گاوسی» (Gaussian Distribution) یا توزیع «گاوس-لاپلاس» (Laplace-Gauss) گفته می‌شود. از آنجایی که این توزیع دارای منحنی به شکل زنگ است، گاهی به آن «منحنی زنگی شکل» (Bell Curve) نیز گفته می‌شود.

قواعد حاکم بر بیشتر پدیده‌های تصادفی در زندگی از توزیع نرمال پیروی می‌کنند و از طرف دیگر طبق قضیه «قضیه حد مرکزی» (Central Limit Theorem) می‌توان توزیع تقریبی پدیده‌های دیگر را نیز نرمال تصور کرد. به همین علت کاربرد این توزیع در همه زمینه‌ها از جامعه شناسی تا پزشکی و مهندسی گسترده است.

در این مطلب به بررسی متغیر تصادفی یک و چند متغیره با توزیع نرمال می‌پردازیم و همچنین در مورد قضیه حد مرکزی نیز بحث خواهیم کرد. برای درک بهتر این نوشتار، بهتر است که ابتدا مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و توزیع نرمال و توزیع نرمال استاندارد — به زبان ساده را که در این لینک در دسترس است مطالعه کنید.

توزیع نرمال و متغیر تصادفی نرمال

اهمیت و کاربرد توزیع نرمال به علت «قضیه حد مرکزی» (Central Limit Theorem) است. این قضیه بیان می‌دارد که برای متغیرهای تصادفی که دارای واریانس متناهی هستند، میانگین‌های نمونه‌های تصادفی متغیرهای تصادفی هم‌توزیع و مستقل (iid) به توزیع نرمال میل خواهند کرد. به همین علت است که توزیع بیشتر کمیت‌های فیزیکی که به صورت جمع چندین فرآیند مستقل بدست می‌آیند، (مثلا خطای اندازه‌گیری) نرمال فرض می‌شود.

فیلم آموزش تئوری احتمالات – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

به همین ترتیب بسیاری از روش‌های دیگر مانند برازش پارامترها به کمک کمترین مربعات زمانی به کار می‌روند که توزیع داده‌ها نرمال باشد. این دلایل، اهمیت توزیع نرمال را در تحلیل داده‌ها مشخص می‌کند.

در سال 1809، «کارل گووس» (Carl Gauss)، فیزیکدان، ریاضیدان و دانشمند آلمانی، به بررسی پدیده‌هایی پرداخت که تابع احتمال آن‌ها به صورت زنگی شکل بود. او در دست‌نوشته‌اش با عنوان «نظریه حرکت اجرام آسمانی در بخش‌های مخروطی خورشید» (Theoria motus corporum coelestium in sectionibus conicis solem ambientium) به بررسی میزان خطا، «روش کمترین مربعات» (Least Square method)، «بیشینه درستنمایی» (Maximum Likelihood) و «توزیع نرمال» (Normal Distribution) پرداخت.

از طرف دیگر لاپلاس (Marquis de Laplace) ریاضیدان، دانشمند آمار و فیزیکدان شهیر  فرانسوی در قرن ۱۸ توانست نشان دهد که $$\int e^{-t^2}dt=\sqrt{\pi}$$ و به این ترتیب توزیع جمع چند متغیر تصادفی را مشخص کرد. او به این ترتیب توانست قضیه حد مرکزی را اثبات کند که در آمار بسیار با اهمیت است.

تابع چگالی احتمال توزیع نرمال

پارامترهای چگالی احتمال برای توزیع نرمال «میانگین» ($$\mu$$) و «انحراف استاندارد» ($$\sigma$$) است و فرم چگالی به صورت زیر نوشته می‌شود.

$$\large {\displaystyle f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}}$$

برای چنین متغیر تصادفی می‌نویسیم $$X\sim N(\mu,\sigma^2)$$ و می‌خوانیم X دارای توزیع نرمال با پارامترهای $$\mu$$ و $$\sigma^2$$ است.

گاهی به میانگین، پارامتر مرکزی و به انحراف استاندارد، پارامتر مقیاس گفته می‌شود زیرا اولی مرکز توزیع و دومی میزان پراکندگی را نشان می‌دهد.

نکته: در این توزیع، میانگین، میانه و نما با یکدیگر برابرند.

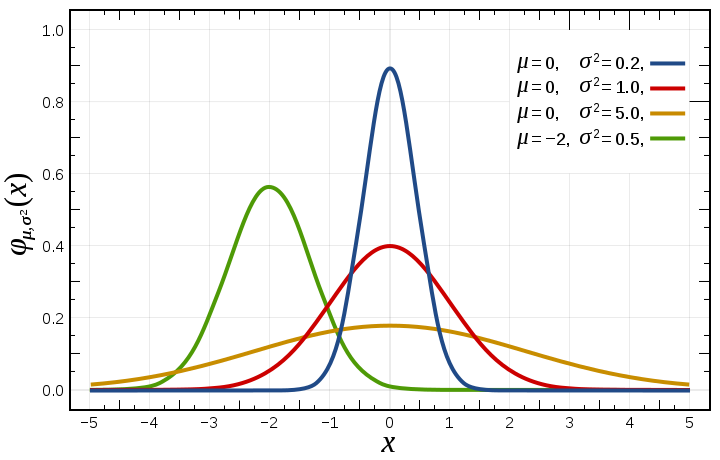
در تصویر بالا، منحنی چگالی احتمال متغیر تصادفی با توزیع نرمال با پارامترهای مختلف ترسیم شده است. همانطور که مشخص است پارامتر میانگین، مرکز ثقل منحنی و واریانس کشیدگی افقی منحنی را تعیین می‌کند. همانطور که مشخص است، تکیه‌گاه برای این متغیر تصادفی، اعداد حقیقی است.

مقدار چگالی احتمال برای این متغیر تصادفی را گاهی به صورت $$\phi_{\mu,\sigma^2}(x)$$ نشان می‌دهند. شکل توزیع تجمعی احتمال $$P(X$$ برای این متغیر تصادفی نیز در شکل زیر ترسیم شده است.

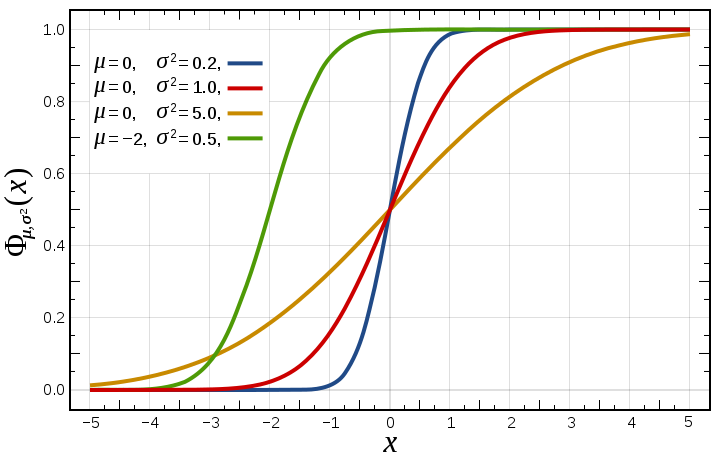
توزیع نرمال استاندارد

شاید ساده‌ترین حالت برای تعیین پارامترهای توزیع نرمال، انتخاب صفر برای میانگین و ۱ برای واریانس باشد. به چنین توزیعی «نرمال استاندارد» (Standard Normal Distribution) گفته می‌شود.

فیلم آموزش توزیع نرمال در آمار و کاربرد آن در علوم انسانی (رایگان) در فرادرس

کلیک کنید

به این ترتیب می‌توان تابع احتمال را برای چنین متغیر تصادفی به صورت زیر نوشت:

$$\large {\displaystyle \varphi (z)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}z^{2}}}$$

در این حالت می‌نویسیم $$Z\sim N(0,1)$$ و می‌خوانیم، Z دارای توزیع نرمال استاندارد است.

نکته: عبارت $$\dfrac{1}{\sqrt{2\pi}}$$ تضمین می‌کند که سطح زیر منحنی $$\phi(z)$$ برای این توزیع برابر با ۱ خواهد بود. عبارت $$\frac{1}{2}$$ در نمای عبارت نیز تضمین می‌کند که واریانس برابر با ۱ است. همچنین با توجه به عبارت $$z^2$$ در چگالی احتمال، مشخص می‌شود که این توزیع متقارن حول صفر است.

با توجه به نمودارهای قبلی و همچنین شکل تابع چگالی احتمال، مشخص است که حداکثر مقدار برای این توزیع در نقطه ۰ بدست می‌آید و مشخص است که مقدار تابع چگالی در این نقطه برابر با $$\dfrac{1}{\sqrt{2\pi}}$$ است. همچنین نقاط عطف برای این تابع در x=1 و x=-1 حاصل می‌شود.

به این ترتیب می‌توان هر توزیع نرمال را براساس توزیع نرمال استاندارد بازنویسی کرد. همچنین محاسبه احتمال برای یک توزیع نرمال، براساس تابع توزیع تجمعی نرمال استاندارد قابل صورت می‌پذیرد. شکل این رابطه در زیر قابل مشاهده است:

$$\large {\displaystyle f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sigma }}\varphi \left({\frac {x-\mu }{\sigma }}\right)}$$

مشخص است که رابطه بین متغیر تصادفی X و Z در این حالت به صورت $$X=\sigma Z+\mu$$ یا $$Z=\dfrac{(X-\mu)}{\sigma}$$ نوشته می‌شود.

تابع توزیع تجمعی (Cumulative Distribution Function)

اگر Z دارای توزیع نرمال استاندارد باشد، تابع توزیع تجمعی آن را براساس انتگرال زیر می‌توان محاسبه کرد.

$$\large {\displaystyle F_Z(z)=P(Z<z)=\Phi (z)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{z}e^{-t^{2}/2}\,dt}$$

همانطور که دیده می‌شود، تابع توزیع تجمعی برای متغیر تصادفی نرمال استاندارد به شکل $$\Phi(x)$$ معرفی شده است.

اگر برای متغیر تصادفی X با توزیع نرمال با میانگین $$\mu$$ و واریانس $$\sigma^2$$ بخواهیم تابع توزیع تجمعی را محاسبه کنیم، بهتر است به کمک رابطه زیر مقدار احتمال را بدست آوریم.

$$F_X(x)=P(X$$

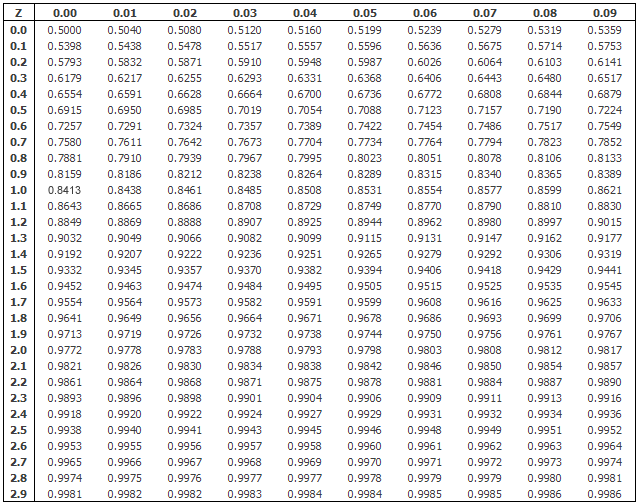
به همین منظور فقط برای توزیع نرمال استاندارد جدول‌هایی احتمال محاسبه شده و در دسترس است. در زیر یک نمونه از این جدول‌ها قابل مشاهده است.

به کمک این جدول می‌توان مقدار احتمال تجمعی را برای هر نقطه، محاسبه کرد. برای مثال اگر به $$P(Z<1.55)$$ احتیاج دارید کافی است از ستون اول (که با علامت Z مشخص شده) مقدار 1.5 و از سطر اول جدول نیز مقدار 0.05 را انتخاب کنید. خانه‌ای از جدول که محل برخورد سطر و ستون حاصل از جستجوی شماست، مقدار احتمال تا نقطه 1.55 را نشان می‌دهد. این مقدار در جدول 0.9394 است.

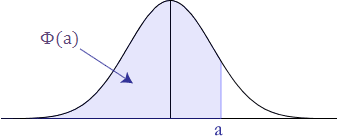
با توجه به تقارن توزیع نرمال استاندارد اگر بخواهیم احتمال $$P(Z<-1.55)$$ را پیدا کنیم (که در جدول دیده نمی‌شود) کافی است به صورت زیر عمل کنیم.

$$P(Z<-1.55)=P(Z>1.55)=1-P(Z<1.55)=1-0.9394=0.6060$$

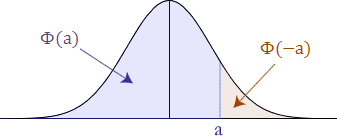
دلیل انجام این کار در تصویرهای زیر به خوبی دیده می‌شود. در ابتدا به دلیل تقارن مشخص است که مقدار $$\Phi(-a)$$ با مقدار احتمال برای مقادیر بزرگتر از a برابر است.

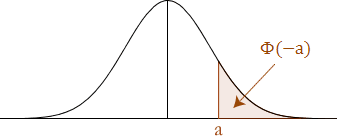
در نتیجه برای محاسبه این احتمال از روی جدول توزیع احتمال تجمعی باید طبق شکل زیر از احتمال متمم پیشامد مورد نظر استفاده کرد.

ترکیب متغیرهای تصادفی نرمال

فرض کنید که $$X_1$$ و $$X_2$$ دارای توزیع نرمال با میانگین صفر و واریانس ۱ باشند. آنگاه می‌توان گفت:

• مجموع $$X_1+X_2$$ دارای توزیع نرمال با میانگین صفر و واریانس ۲ است. حتی می‌توان نوشت: $$X_1\pm X_2\sim N(0,2)$$
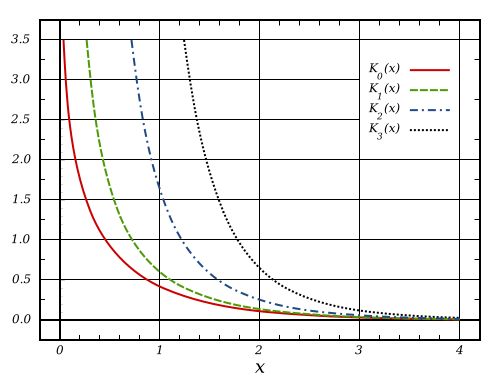
• حاصل‌ضرب این دو متغیر تصادفی (بدون در نظر گرفتن استقلال) دارای توزیع «حاصلضرب نرمال» (Product-Normal) است که چگالی آن به صورت $$f_Z(z) = \pi^{−1}K_0(|z|)$$ است که در آن $$k_0$$ تابع تغییر یافته بسل از نوع دوم (Modified Bessel Function of the Second Kind) است. این توزیع حول صفر متقارن و در z=0 نامتناهی می‌شود. همچنین تابع مشخصه این توزیع به صورت  $$\varphi_{Z}(t)=(1 + t^2)^{−1/2}$$ نوشته می‌شود.

• نسبت دو متغیر تصادفی $$X_1$$ و $$X_2$$ دارای توزیع کوشی است و به این ترتیب می‌توان نوشت $$\dfrac{X_1}{X_2}\sim Cauchy(0,1)$$.

توزیع نرمال چند متغیره و متغیر تصادفی آن

فرض کنید متغیر تصادفی  $$\bf {X}$$ دارای k بعد باشد. اگر تابع چگالی احتمال آن را بتوان به شکل زیر نوشت، می‌گوییم $$\bf {X}$$ دارای توزیع چند متغیره نرمال با پارامترهای $${\displaystyle \bf {\mu}}$$ و $$\boldsymbol{\Sigma}$$ است و می‌نویسیم:

$$\large {\displaystyle \mathbf {X} \ \sim \ {\mathcal {N}}({\boldsymbol {\mu }},\,{\boldsymbol {\Sigma}})}$$

باید توجه داشت که در اینجا همه متغیرها و پارامترها k بعدی هستند. مشخص است که در اینجا برای پارامتر میانگین ($$\boldsymbol {\mu}$$) خواهیم داشت:

$$\large{\displaystyle {\boldsymbol {\mu }}=\operatorname {E} [\mathbf {X} ]=[\operatorname {E} [X_{1}],\operatorname {E} [X_{2}],\ldots ,\operatorname {E} [X_{k}]]^{\rm {T}}}$$

همچنین برای ماتریس واریانس-کوواریانس $$\boldsymbol {\Sigma}$$ که یک ماتریس $$k\times k$$ بعدی است، می‌توان نوشت:

$$\large{\displaystyle {\boldsymbol {\Sigma }}=\operatorname {E} [(\mathbf {X} -{\boldsymbol {\mu }})(\mathbf {X} -{\boldsymbol {\mu }})^{\rm {T}}]=[\operatorname {Cov} [X_{i},X_{j}];1\leq i,j\leq k]}$$

در اینجا منظور از E همان امید ریاضی متغیر تصادفی X و COV نیز کوواریانس را نشان می‌دهد. شکل نمایش تابع چگالی برای چنین متغیر تصادفی به صورت زیر است.

$$\large {\displaystyle {\begin{aligned}f_{\mathbf {X} }(x_{1},\ldots ,x_{k})&={\frac {\exp \left(-{\frac {1}{2}}({\mathbf {x} }-{\boldsymbol {\mu }})^{\mathrm {T} }{\boldsymbol {\Sigma }}^{-1}({\mathbf {x} }-{\boldsymbol {\mu }})\right)}{\sqrt {(2\pi )^{k}|{\boldsymbol {\Sigma }}|}}}\end{aligned}}}$$

باید توجه داشت که در این رابطه منظور از $${\displaystyle |{\boldsymbol {\Sigma }|}}$$ همان دترمینان ماتریس $$\Sigma$$ و علامت T نیز نشان‌دهنده ترانهاده بردار  است. بنابراین بردار $$X = (X_1, …, X_k)^T$$ دارای توزیع نرمال چند متغیره است اگر یکی از شرایط زیر را داشته باشد:

• هر ترکیب خطی از اجزای آن (برای مثال $$Y = a_1X_1 + … + a_kX_k$$) دارای توزیع نرمال باشد. به بیان دیگر متغیر تصادفی $$Y = \bf{a}^T\bf{X}$$ دارای توزیع نرمال یک متغیره باشد.
• برای بردار Z با مولفه‌هایی که دارای توزیع نرمال یک متغیره استاندارد مستقل از یکدیگر هستند داشته باشیم: $$X=AZ+\mu$$ بطوری که $$AA^T=\Sigma$$ ماتریس کوواریانس برای X و $$\mu$$ نیز بردار میانگین مولفه‌های X باشد.
• اگر برای بردار kبعدی $$\mu$$ و ماتریس نیمه معین مثبت $$\Sigma$$ تابع مشخصه X به صورت زیر باشد:

$$\large {\displaystyle \varphi _{\mathbf {X} }(\mathbf {u} )=\exp {\Big (}i\mathbf {u} ^{T}{\boldsymbol {\mu }}-{\tfrac {1}{2}}\mathbf {u} ^{T}{\boldsymbol {\Sigma }}\mathbf {u} {\Big )}}$$

توزیع نرمال دو متغیره

در حالتی که متغیر تصادفی X دو بعدی باشد، بردار میانگین و ماتریس واریانس و کوواریانس به صورت زیر نوشته می‌شوند.

$$\displaystyle {\boldsymbol {\mu }}={\begin{pmatrix}\mu _{X}\\\mu _{Y}\end{pmatrix}},\quad {\boldsymbol {\Sigma }}={\begin{pmatrix}\sigma _{X}^{2}&\rho \sigma _{X}\sigma _{Y}\\\rho \sigma _{X}\sigma _{Y}&\sigma _{Y}^{2}\end{pmatrix}}$$

البته برای نمایش تابع چگالی متغیر تصادفی نرمال دو بعدی، می‌توان فرمی خارج از شکل ماتریسی به صورت زیر نیز در نظر گرفت.

$${\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left[{\frac {(x-\mu _{X})^{2}}{\sigma _{X}^{2}}}+{\frac {(y-\mu _{Y})^{2}}{\sigma _{Y}^{2}}}-{\frac {2\rho (x-\mu _{X})(y-\mu _{Y})}{\sigma _{X}\sigma _{Y}}}\right]\right)}$$

در اینجا مشخص است که مقدار $$\rho$$ نشان‌دهنده مقدار ضریب همبستگی پیرسون بین دو متغیر X , Y است.

در تصویر زیر رویه مربوط به چگالی نرمال دو متغیره ترسیم شده است. تقارن و نقطه میانگین که در نقطه (5۰و5۰) قرار دارد در این شکل دیده می‌شود.

قضیه حد مرکزی (Central Limit Theorem)

قضیه حد مرکزی تحت شرایط معمول، بیان می‌دارد که جمع چندین متغیر تصادفی، دارای توزیع نرمال است. به صورت خاص در مورد این قضیه می‌توان گفت که اگر $$X_1,X_2,\cdots,X_n$$ متغیرهای تصادفی هم توزیع و مستقل (iid) با میانگین صفر و واریانس $$\sigma^2$$ باشند، آنگاه با افزایش n، توزیع Z که به صورت زیر تعریف می‌شود، نرمال با میانگین صفر و واریانس $$\sigma^2$$ خواهد بود.

$$\large {\displaystyle Z={\sqrt {n}}\left({\frac {1}{n}}\sum _{i=1}^{n}X_{i}\right)}$$

در بسیاری از آماره‌های آزمون، برآوردگرها و ... از این خاصیت استفاده کرده و برای مجموع یا میانگین متغیرهای تصادفی مستقل و هم توزیع، چگالی احتمال را نرمال در نظر می‌گیرند.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

این قضیه حتی برای توزیع‌های گسسته نیز صادق است. می‌توانید به کمک تصویری که در زیر نمایش داده شده این واقعیت را به خوبی ببینید.

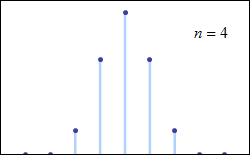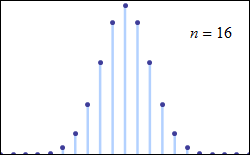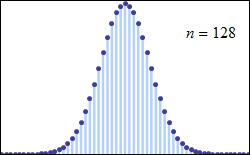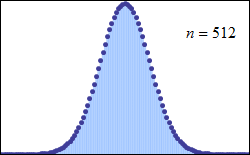
به عنوان کاربردهایی از این قضیه می‌توان به گزاره‌های زیر اشاره کرد:

• به عنوان یک تقریب برای احتمال در توزیع دو جمله‌ای با پارامترهای $$B(n,p)$$ می‌توان از توزیع نرمال با میانگین np و واریانس $$np(1-p)$$ استفاده کرد در صورتی که n بزرگ باشد ولی p به صفر یا ۱ خیلی نزدیک نباشد.
• برای توزیع پواسن با پارامتر $$\lambda$$، می‌توان از توزیع نرمال با میانگین $$\lambda$$ و واریانس $$\lambda$$ استفاده کرد، به شرطی که مقدار $$\lambda$$ بزرگ باشد.
• تقریب محاسبه تابع توزیع احتمال برای توزیع کای ۲، توسط توزیع نرمال با میانگین $$\kappa$$ و واریانس $$2\kappa$$ انجام می‌شود، به شرطی که $$\kappa$$ بزرگ باشد.
• توزیع t برای مقدارهای بزرگ $$\nu$$ به توزیع نرمال با میانگین صفر و واریانس ۱ میل می‌کند.

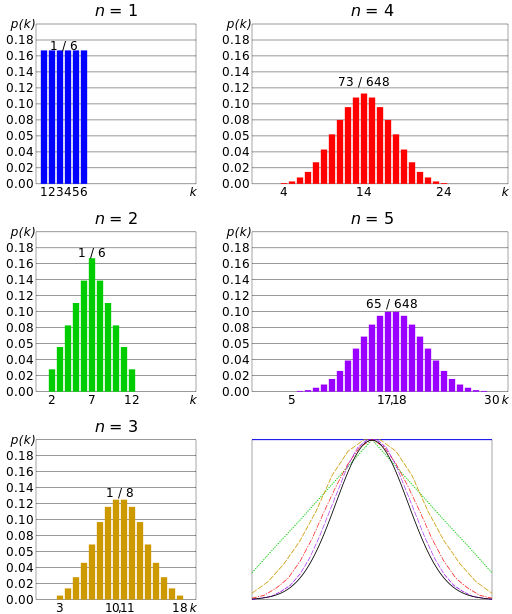
در تصویر زیر تمایل مقدار احتمال برای مجموع اعداد مشاهده شده از پرتاب یک تاس با توجه به تعداد پرتا‌ب‌ها مشخص شده است. برای یکبار پرتاب تاس، مشخص است که احتمال مشاهده هر یک از اعداد برابر با 1/6 است. ولی با افزایش تعداد پرتاب‌ها احتمال مشاهده برای مجموع ارقام متفاوت است. برای مثال اگر تاس را سه بار پرتاب کنیم، حداقل مقدار برابر با ۳ و حداکثر مقدار ۱۸ خواهد بود. در هر بار پرتاب تاس، متغیر تصادفی X که مشاهده شماره تاس است دارای توزیع یکنواخت گسسته است. ولی همانطور که می‌بینید مجموع این متغیرهای تصادفی با افزایش تعداد پرتاب‌ها به سمت نرمال میل خواهد کرد.

اگر به فراگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آزمایش تصادفی، پیشامد و تابع احتمال
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش آزمون های فرض مربوط به میانگین جامعه نرمال در SPSS
• آموزش آزمون آماری و پی مقدار (p-value)
• جامعه آماری — انواع داده و مقیاس‌های آن‌ها
•  تحلیل‌ها و آزمون‌های آماری — مفاهیم و اصطلاحات
• آزمون فرض میانگین جامعه در آمار — به زبان ساده
• فاصله اطمینان (Confidence Interval) — به زبان ساده

^^