تابع گویا و خصوصیات آن | به زبان ساده

یک تابع گویا در ریاضیات، تابعی است که به صورت کسر قابل بیان است. به عنوان مثال یک تابع جبری که به صورت کسر بیان شده و صورت و مخرج آن «چند جمله‌ای» (Polynomial) باشند، یک تابع کسری از نوع گویا خواهد بود. البته لزومی ندارد که ضرایب این چند جمله‌ای‌ها، گویا باشند. در ادامه مثالی از تابع گویا خواهیم داشت که ضرایب آن از اعداد مختلط است. این نوشتار از مجله فرادرس را به بررسی تابع گویا و خصوصیات آن اختصاص داده‌ایم تا ویژگی‌های آن را بهتر درک کنیم.

به منظور آشنایی بیشتر با مفهوم تابع و انواع آن، بهتر است نوشتارهای رابطه و تابع از نگاه مجموعه‌ ها — به زبان ساده و مفاهیم تابع – به زبان ساده را مطالعه کنید. همچنین خواندن مطالب مجموعه ها در ریاضیات – مفاهیم پایه و تابع نشانگر و خصوصیات آن — به زبان ساده نیز خالی از لطف نیست.

تابع گویا و خصوصیات آن

تابع $$f(x)$$ را یک «تابع گویا» (Rational Function) می‌نامند اگر و فقط اگر بتوان آن را به صورت زیر برحسب دو تابع «چند جمله‌ای» (Polynomial) مانند $$P(x)$$ و $$Q(x)$$ نوشت.

$$\large f(x) = {\frac {P(x)} { Q(x) } }$$

واضح است که مخرج این کسر نباید صفر باشد. به این ترتیب دامنه تابع $$f$$، برابر با مجموعه مقادیری از اعداد حقیقی (مختلط) مثل $$x$$ است که مخرج کسر صفر نباشد. توجه داشته باشید که هر «تابع چند جمله‌ای» (Polynomial Function) با قرار دادن مقدار (۱) در مخرج آن، به عنوان چند جمله‌ای $$Qx(x)$$ یا «تابع ثابت» (Constant Function) در نقطه ۱، تبدیل به یک تابع گویا خواهد شد.

فیلم آموزش حسابان ۱ – پایه یازدهم در فرادرس

کلیک کنید

به این ترتیب توابع چند جمله‌ای به نوعی زیرمجموعه‌ای از توابع گویا محسوب می‌شوند. البته توجه داشته باشید که توابع گویا را برحسب توابع چند جمله‌ای معرفی و ساخته‌ایم و از طرفی ادعا می‌کنیم که هر تابع چند جمله‌ای، یک تابع گویا است. این موضوع شاید در ابتدا یک تناقض به نظر برسد، ولی توجه داشته باشید که تعریف توابع چند جمله‌ای برحسب تابع گویا صورت نمی‌گیرد. ولی در شرایطی که گفته شد، تابع گویا و چند جمله‌ای یکسان هستند.

نکته: اگر دو تابع $$P$$ و $$Q$$، دارای «چند جمله‌ای بزرگترین مقسوم علیه مشترک غیر ثابت» (Non-Constant Polynomial Greatest Common Divisor) مثل $$R$$ باشند، آنگاه می‌توان تابع $$f_1$$ و $$f$$ را بروی دامنه $$f$$، یکسان در نظر گرفت.

$$\large f_{1} ( x ) = { \frac {P_{1} ( x ) } { Q _  1 (x)} }$$

توجه داشته باشید که در رابطه بالا بین $$P(x)$$ و $$P_1(x)$$ رابطه زیر برقرار است.

$$\large P = P_1 R$$

که در آن $$R$$‌ همان «چند جمله‌ای بزرگترین مقسوم علیه مشترک» (Polynomial Greatest Common Divisor) است. همچنین برای تابع $$Q$$ و $$Q_1$$ نیز خواهیم داشت:

$$\large Q = Q_1 R$$

ممکن است که دامنه تابع $$f_1$$ بزرگتر از دامنه تابع $$f$$ ‌باشد ولی روی اشتراک دامنه آن‌ها، رابطه تساوی $$f=f_1$$ برقرار است. «تابع گویا سره» (Proper Rational Function)، نیز تابع گویایی است که درجه چند جمله‌ای صورت آن از درجه چند جمله‌ای مخرج، کوچکتر باشد. این ویژگی باعث می‌شود که در چنین کسری، ساده‌سازی صورت نگرفته و نتوان درجه صورت را تقلیل داد.

نکته: به یاد دارید که درجه چند جمله‌ای، بزرگترین توان عبارت‌های چندجمله‌ای محسوب می‌شود.

درجه تابع گویا

تعریف‌های متنوع و گوناگونی برای تعیین درجه تابع گویا وجود دارد. در بعضی از کتاب‌های مرجع ریاضیات، «درجه تابع گویا» (Degree of Rational Function)، بزرگترین درجه چندجمله‌هایی تشکیل دهنده تابع گویا (چند جمله‌ای صورت $$P(x)$$ و مخرج $$Q(X)$$) در نظر گرفته می‌شود. البته توجه داشته باشید که در این حالت باید صورت و مخرج ساده شده و به صورت جمله‌هایی با کوچکترین توان‌ها نوشته شوند، یعنی تابع گویا از نوع سره باشد.

به این ترتیب اگر درجه تابع گویا $$f$$ برابر با $$d$$ باشد، آنگاه معادله زیر

$$\large f(z) = w \,$$

دارای $$d$$ پاسخ برای $$z$$ است به جز در نقاطی از $$w$$ که به آن‌ها «مقادیر بحرانی» (Critical Values) گفته می‌شود. تابع $$f$$ ممکن است در نقاط بحرانی دارای دو ریشه برابر (ریشه مضاعف) بوده یا در بعضی از آن‌ها بی‌نهایت شود.

نکته: اگر ضرایب چندجمله‌ای‌ها، «اعداد مختلط» (Complex Number) باشند، تابع گویا با درجه ۱، همان «تبدیل موبیوس» (Mobius Transformation) خواهد بود.

توجه داشته باشید که درجه نمودار یا «درجه گراف» (Graph Degree) تابع گویا، به ترتیبی که در قبل گفته شد، حاصل نمی‌شود. درجه صورت و درجه مخرج تابع گویا را در نظر بگیرید. بزرگترین مقدار درجه صورت و حاصل جمع درجه مخرج با ۱، نشانگر درجه نمودار یا گراف تابع گویا خواهد بود. این موضوع در مثال ۱ مورد بررسی قرار خواهد گرفت. در ضمن در بعضی از کتاب‌‌های ریاضیات، بخصوص در مبحث «تحلیل مجانبی» (Asymptotic Analysis)، درجه گراف تابع گویا، از تفاضل درجه صورت و مخرج حاصل می‌شود.

یکی از ویژگی‌های جالب برای تابع گویا بسته بودن نسبت به عملگرهای حسابی است. توابع گویا نسبت به عمل جمع، ضرب و تقسیم (به جز تقسیم بر چند جمله‌ای صفر) بسته هستند. به این ترتیب اگر دو تابع گویا را با یکدیگر جمع یا ضرب کنیم، حاصل نیز یک تابع گویا خواهد بود. این موضوع در مورد تقسیم دو تابع گویا نیز صادق است، به شرطی که مخرج تابع گویا صفر نباشد.

مثال‌هایی از تابع گویا

در ادامه به مثال‌هایی از توابع گویا می‌پردازیم و درجه هر یک از آن‌ها را محاسبه می‌کنیم. توجه داشته باشید که هر تابع باید به همراه دامنه‌اش مشخص شده، یا حداقل نقاطی که تابع در آن‌ها تعریف نشده معین شوند.

مثال ۱: تابع گویا زیر را در نظر بگیرید.

$$\large f(x) = {\frac {x^{3} - 2 x }{2(x^{2} - 5 )}}$$

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

این تابع در نقطه $$\sqrt{5}$$ و $$-\sqrt{5}$$ تعریف نشده است، زیرا:

$$\large {\displaystyle x^{2} = 5 \Leftrightarrow x = \pm { \sqrt { 5 } } }$$

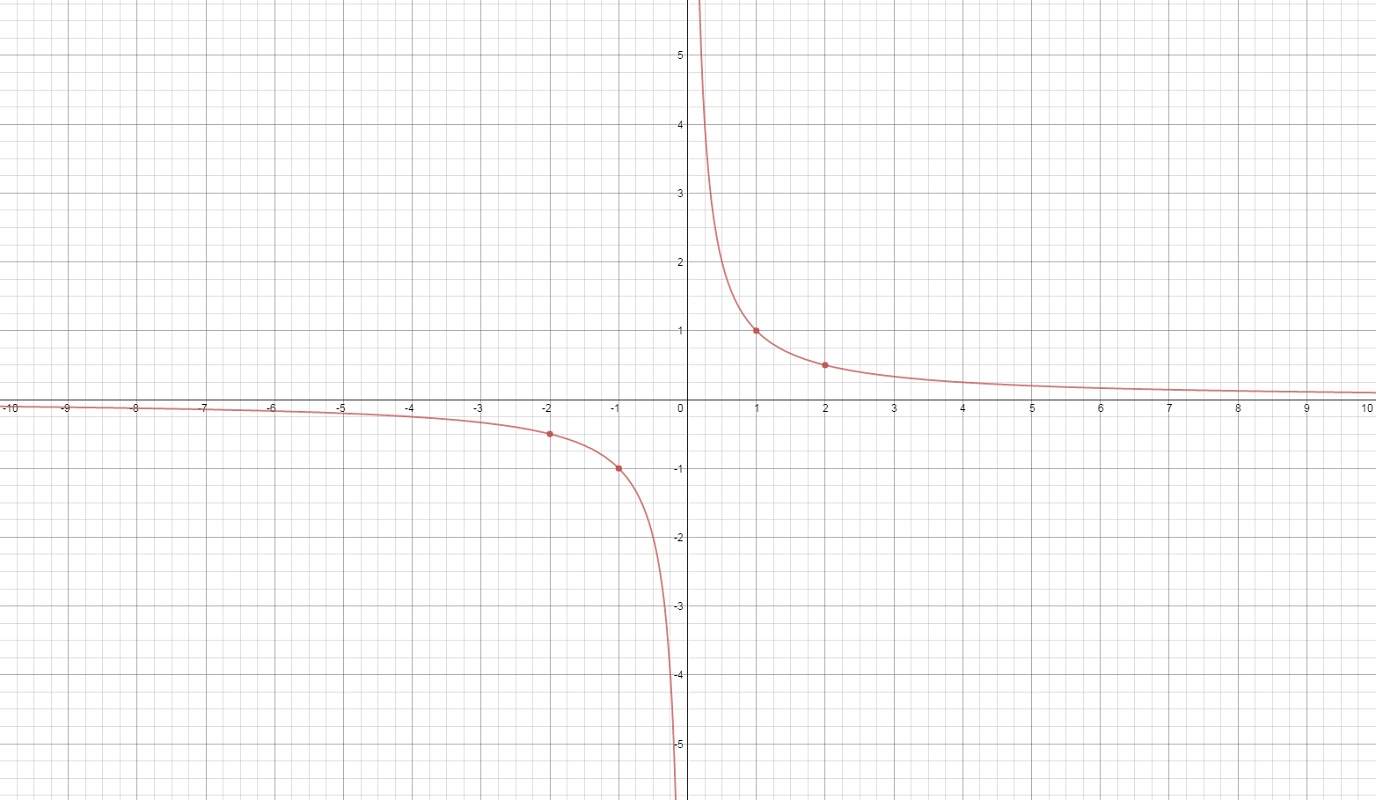
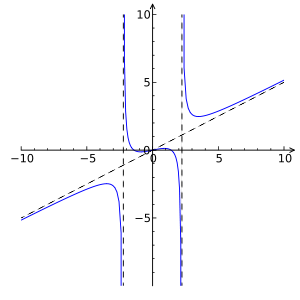
بنابراین دامنه این تابع گویا، شامل این دو نقطه نخواهد بود. از طرفی خط مجانب نیز به شکل $$\frac{x}{2}$$‌ است، زیرا به کمک محاسبه حد این تابع در بی‌نهایت داریم:

$$\large \lim_{x \rightarrow \infty} {\frac {x^{3} - 2 x }{2(x^{2} - 5 )}} = \dfrac{x}{2} .$$

نمودار این تابع و همچنین خط مجانب آن را در تصویر ۱ مشاهده می‌کنید. در ضمن با توجه به تعریف ارائه شده برای تابع گویا و درجه نمودار یا گراف آن، مشخص است که درجه این تابع برابر با ۳ خواهد بود. در ضمن درجه گراف با درجه تابع برابر است.

مثال ۲: تابع گویای زیر روی همه مقادیر اعداد حقیقی، تعریف شده است، زیرا مخرج آن هرگز صفر نخواهد بود.

$$\large g(x) = { \frac {x^{2} + 2 }{ x^{2} + 1 } }$$

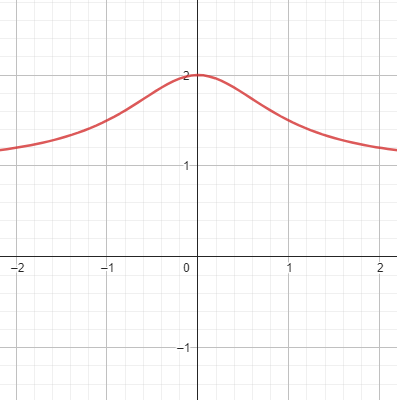
در تصویر ۲، نمودار تابع $$g(x)$$ را در مجموعه اعداد حقیقی (مختصات دکارتی) مشاهده می‌کنید. توجه داشته باشید که با در نظر گرفتن اعداد مختلط، با مقدار $$x = i = \sqrt{-1}$$، مخرج کسر، برابر با صفر خواهد شد. فرض کنید $$x = i$$ عدد مختلط باشد. آنگاه تابع در این نقطه تعریف نشده است.

$$\large {\displaystyle g(i) = { \frac {i^{2} + 2 }{i^{2} + 1 } } = { \frac { - 1 + 2 }{ - 1 + 1 } } = { \frac {1}{0}}}$$

مثال ۳: «تابع ثابت» (Constant Function)، مانند $$h(x) = \pi$$ یک تابع گویا است. زیرا مقدار ثابت نیز به صورت یک چند جمله‌ای قابل نمایش است. چنین تابعی گویا است حتی اگر مقدار آن به ازاء هر مقدار از $$x$$، مختلط باشد.

مثال ۴: همانطور که در ابتدای متنی نیز اشاره کردیم، هر تابع چند جمله‌ای، یک تابع گویا است. برای تابع گویا $$f$$ رابطه زیر را در نظر بگیرید.

$$\large f(x) = {\frac {P(x)} { Q(x) } }$$

که در آن $$f(x) = P(x)$$ یک چند جمله‌ای و $$Q(x) = 1$$‌ باشد. در صورتی که $$P(x)$$ چند جمله‌ای نباشد، چنین تابعی، گویا نخواهد بود. برای مثال اگر $$f(x) = sin(x)$$‌ در نظر گرفته شود، نمی‌توانیم آن را تابع گویا در نظر بگیریم.

نکته: معمولا برای تابعی که گویا نیست از اصطلاح «غیرگویا» (Irrational) استفاده نمی‌شود.

مثال ۵: تابع $$f(x) = \dfrac{x}{x}$$ که برابر با ۱ است، یک تابع گویا است. البته واضح است که دامنه این تابع شامل صفر نخواهد بود.

بسط تیلور

ضرایب «سری تیلور» (Tailer Series) هر تابع گویا، در «رابطه خطی بازگشتی» (Linear Recurrence Relation) مرتبط با آن، صدق می‌کنند و می‌توانیم این ضرایب را به وسیله عملیاتی که در ادامه معرفی خواهیم کرد، بدست آوریم. به این منظور با معادل قرار دادن تابع گویا با یک سری تیلور با ضرایب نامعین و اجرای بعضی از اصلاحات، پس از ساده‌سازی جملات هم‌سان، ضرایب مشخص می‌شوند. برای مثال تابع گویای زیر را در نظر بگیرید که با یک سری تیلور با ضرایب فرضی، در یک معادله قرار گرفته‌اند.

$$\large {\frac {1}{x^{2} - x + 2 }} = \sum _{k = 0 }^{\infty }a_{k}x^{k}$$

می‌خواهیم ضرایب بسط تیلور را برای تعیین مقدار تابع گویا (به صورت تقریبی) مشخص کنیم. به این ترتیب قادر هستیم یک تابع گویا را به صورت یک تابع چند جمله‌ای نوشته و مقدار آن را تقریب بزنیم. این موضوع بخصوص در محاسبات رایانه‌ای بسیار اهمیت دارد.

با ضرب کردن دو طرف رابطه بالا در مخرج عبارت سمت چپ، خواهیم داشت:

$$\large 1 =(x^{2} - x + 2 )\sum _{ k = 0 }^{\infty } a_{k} x^{k}$$

و به این ترتیب داریم:

$$\large 1 = \sum _{ k = 0 }^{\infty } a_{k} x^{ k + 2 } - \sum _{ k = 0 }^{ \infty } a_{k} x^{k + 1 } + 2\sum _{ k = 0}^{\infty } a_{k} x^{k}$$

بعد از تنظیم کردن اندیس جمع‌ها به منظور یکسان سازی توان متغیر $$x$$ به رابطه زیر خواهیم رسید.

$$\large 1 = \sum _{ k = 2}^{\infty } a_{ k - 2} x^{k} - \sum _{ k = 1}^{\infty } a_{ k - 1} x^{k} + 2 \sum _{k = 0}^{\infty } a_{k} x^{k}$$

همچنین در انتها، عبارت‌های هم درجه با یکدیگر ترکیب کرده و رابطه زیر ساخته می‌شود.

$$\large 1 = 2 a_{0} + ( 2 a_{1} - a_{0}) x + \sum _{k = 2 }^{ \infty }( a_{ k - 2} - a_{k - 1} + 2 a_{k}) x^{k}$$

از آنجایی که رابطه اخیر برای همه $$x$$ها در شعاع همگرایی دنباله یا سری تیلور برقرار است، محاسبات را به صورت زیر ادامه می‌دهیم.

از آنجایی که عبارت ثابت در سمت چپ رابطه بالا باید برابر با مقدار ثابت در سمت راست رابطه باشد، داریم:

$$\large a_{0} = {\frac {1}{2}}$$

از طرفی در سمت چپ، هیچ جمله‌ای بر حسب $$x$$ حضور ندارد، پس باید همه ضرایب $$x$$ها صفر باشند. بنابراین برای قسمت اول رابطه یا عبارت سمت راست، خواهیم داشت:

$$\large 2a_1 - a_0 = 0 \xrightarrow {a_0 = \frac{1}{4} } 2a_1 = \frac{1}{4}$$

بنابراین حاصل برای عبارت $$a_1$$ بدست می‌آید.

$$\large a_{1}={\frac {1}{4}}$$

به همین ترتیب نیز برای ضریب جملات توان‌دار $$x$$ که در قسمت جمع رابطه نوشته شده‌اند، نیز باید داشته باشیم:

$$\large a_{k - 2} - a_{k - 1} + 2 a_{k}= 0$$

در نتیجه به رابطه برگشتی زیر خواهیم رسید.

$$\large a_{k} = {\frac {1}{2}}(a_{k - 1} - a_{k - 2}) \quad for \;\; k \geq 2$$

در مقابل، دنباله‌هایی که هنگامی که به عنوان ضرایب یک سری تیلور مورد استفاده قرار گیرد و در رابطه بازگشتی خطی صدق کنند، می‌توانند یک تابع گویا را ایجاد نمایند. این امر برای پیدا کردن ریشه‌های توابع گویا بسیار مفید است، زیرا با استفاده از تجزیه جزئی می‌توانیم هر «تابع گویا سره» (Proper Rational Function) را به عنوان مجموعه‌ای از فاکتورها به فرم $$\frac{a x + b }{2}$$ نوشته و این عمل‌ را به شکل سری یا «دنباله هندسی» (Geometric Series) گسترش دهیم. در انتها نیز به کمک رابطه‌های ایجاد شده، یک فرمول صریح را برای دنباله تیلور ارائه نماییم. این روش در ریاضیات به نام تکنیک «تابع مولد» (Generating Function) معروف است. در تصویر ۳، نمونه‌ای از توابع مولد برای چند تابع گویا مشاهده می‌کنید.

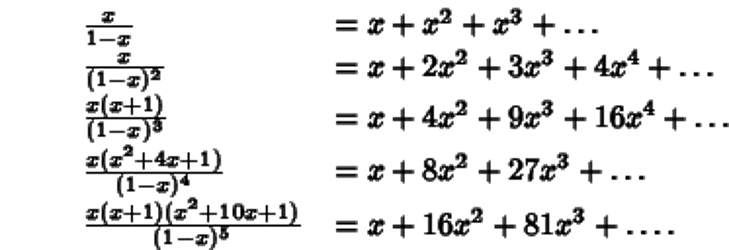
تابع گویا در آنالیز مختلط

در «تحلیل توابع مختلط» (Complex Analysis)، تابع گویا از نسبت یا تقسیم دو چند جمله‌ای با ضرایب مختلط ایجاد می‌شود، بطوری که $$Q$$ چند جمله‌ای با مقدار صفر نیست و P و Q هیچ عامل فاکتور مشترکی ندارند (با این کار از ظاهر شدن کسر 0/0 جلوگیری می‌شود).

$$\large {\displaystyle f (z) = \frac {P (z)} {Q (z)}}$$

دامنه تابع f مجموعه‌ای از اعداد مختلط است به گونه‌ای که

$$\large  {\displaystyle Q (z) \neq 0 }$$

به این ترتیب دامنه چنین تابعی، شامل مجموعه‌ای از اعداد مختلط ($$w$$) است که در رابطه زیر صدق کنند:

$$\large {\displaystyle P (z) \neq w Q (z) } .$$

هر تابع گویا را می‌توان به طور طبیعی به تابعی گسترش داد که دامنه و برد آن کل «کره ریمان» (Reimman Sphere) باشد. توابع گویا، نماینده «توابع مرومورفیک» (Meromorphic function) هستند. در مورد این دو مفهوم در نوشتارهای بعدی مجله فرادرس صحبت خواهیم کرد.

کاربردهای تابع گویا در ریاضیات

احتمالا اولین بار، با توابع گویا در درس جبر دبیرستان مواجه شده‌اید. در ریاضیات پیشرفته‌تر آنها نقش مهمی در «نظریه حلقه» (Ring Theory) به ویژه در «ساختار توسعه میدان» (Construction of Field Extension) دارند. توابع گویا، در تجزیه و تحلیل عددی برای درون‌یابی و تقریب توابع دیگر نیز مورد استفاده قرار می‌گیرند. به عنوان مثال تقریب Padé یا (Padé approximations)، معرفی شده توسط «هنری پاد» (Henri Padé)، یکی از کاربردهای توابع گویا محسوب می‌شود. این تقریب بوسیله عبارت‌هایی ساخته شده از توابع گویا برای سیستم‌های جبری رایانه و سایر نرم‌افزارهای عددی مناسب است.

فیلم آموزش ریاضی 2 – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

درست به مانند توابع چند جمله‌‌ای، توابع گویا نیز می‌توانند به صورت مستقیم محاسبه شوند و در عین حال رفتار پیچیده‌تری نسبت به توابع چند جمله‌ای از خود نمایش می‌دهند. توابع گویا برای تقریب یا الگوسازی معادلات پیچیده در علوم و مهندسی شامل میدان‌ها و نیروها در فیزیک، طیف سنجی در شیمی تحلیلی، سینتیک آنزیم در بیوشیمی، مدارات الکترونیکی، آیرودینامیک، غلظت دارو در داخل بدن، توابع موج برای اتم‌ها و مولکول‌ها، اپتیک استفاده می‌شوند. همچنین در عکاسی برای بهبود وضوح تصویر و صدا و صدا نیز توابع گویا کاربرد دارند.

فیلم آموزش ریاضی و آمار 2 – پایه یازدهم علوم انسانی در فرادرس

کلیک کنید

در «پردازش سیگنال» (Signal Processing)، «تبدیل لاپلاس» (Laplace Transformation) روی سیستم‌های پیوسته، همچنین برای تبدیل z (سیستم‌های گسسته) در «پاسخ ضربه» (Impulse response) و سیستم‌های ثابت خطی نامتغیر با زمان (فیلترها) با پاسخ ضربه نامتناهی، توابع گویا با دامنه اعداد مختلط به کار گرفته می‌شوند.

خلاصه و جمع‌بندی

در این نوشتار با تابع گویا که نوعی تابع کسری محسوب می‌شود آشنا شدیم. همانطور که دیدید، تابع گویا و خصوصیات آن در ریاضیات مورد توجه بوده و بخصوص در جبر، قضیه‌ها و گزاره‌های مهمی در مورد آن نوشته و اثبات شده است. رسم توابع گویا به علت رفتار مجانبی آن‌ها از اهمیت زیادی برخوردار است. بسط تیلور نیز همانطور که دیدید، گونه‌ای از تبدیل تابع گویا به چند جمله‌ای است که منجر به یک تابع مولد خواهد شد. کاربرد توابع گویا در مهندسی، علوم پزشکی و شیمی و عکاسی نیز دیده می‌شود.