انتگرال فوریه و محاسبه آن – به زبان ساده (+ دانلود فیلم آموزش رایگان)
در آموزشهای قبلی مجله فرادرس، درباره سری فوریه و تبدیل فوریه صحبت کردیم. در این آموزش، به بررسی انتگرال فوریه یا فرم انتگرالی سری فوریه میپردازیم.
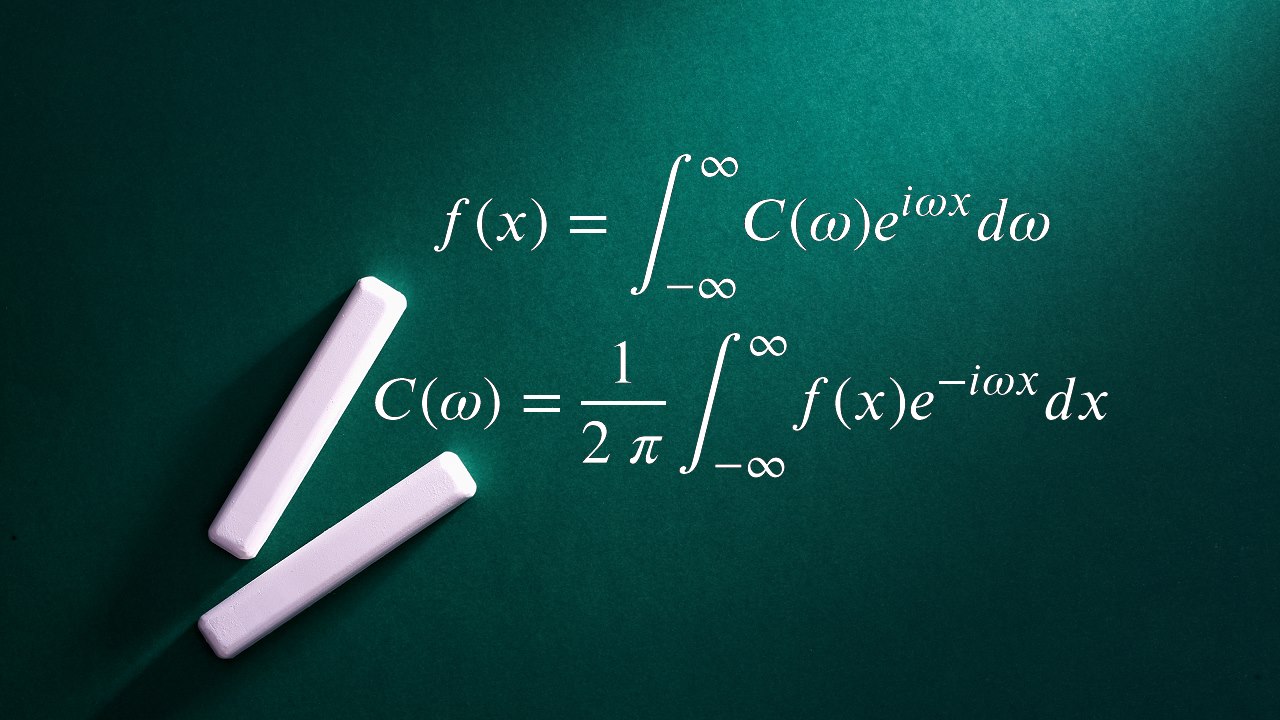
سری فوریه
در آموزش مربوط به سری فوریه مختلط، دیدیم که میتوان سری فوریه را به فرم مختلط زیر نوشت:
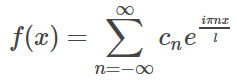
که در آن:
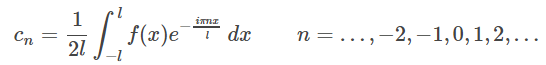
همچنین:
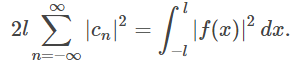
از سه معادله گفته شده در بالا، میتوان فرم صریح انتگرال فوریه را محاسبه کرد.
انتگرال فوریه
ابتدا توابع زیر را تعریف میکنیم:
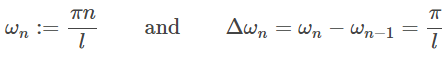
بنابراین، میتوان معادله (۱) را به فرم زیر نوشت:
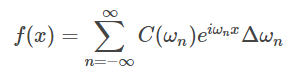
که در آن:
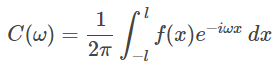
در معادله (۵)، از رابطه زیر استفاده شده است:
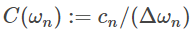
معادله (۳) را میتوان به شکل زیر بازنویسی کرد:
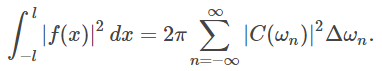
حال فرض کنید به سمت بینهایت میل کند، یعنی:
بنابراین سمت راست معادله (۶) و همچنین سمت چپ معادله (۷)، به انتگرالهایی از تا تبدیل میشوند.
فرض میشود:
پس «جمع ریمانی» (Riemann sum)، در سمت راست معادلات (۵) و (۷)، تبدیل به انتگرال میشود. میتوان معادله (۵) را به صورت زیر بازنویسی کرد:
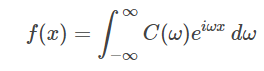
که در آن:
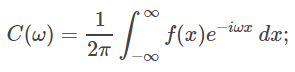
پس معادله (۳) به شکل زیر نوشته میشود:
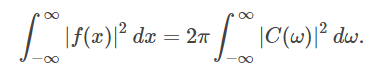
تعاریف
در ادامه، به بررسی چند تعریف برای فرم انتگرالی سری فوریه پرداخته میشود.
تعریف ۱
معادله (۹) به نام تبدیل فوریه تابع مشهور است و به صورت زیر تعریف میشود:
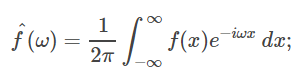
البته تبدیل فوریه را به صورت یا نیز نمایش میدهند.
تعریف ۲
معادله (۸) به نام انتگرال فوریه یا معکوس تبدیل فوریه مشهور است. انتگرال فوریه به صورت زیر نشان داده میشود:
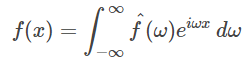
میتوان فرم انتگرالی فوریه را به صورت معکوس تبدیل فوریه نوشت. به صورت زیر:
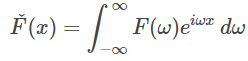
نکته 1: معادله (۱۰) به «قضیه پلانچرل» (Plancherel Theorem) نیز مشهور است. بیان قضیه پلانچرل به صورت زیر است:
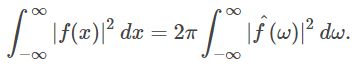
نکته 2:
الف) در برخی موارد، توان نمایی با جایگزین و ضریب حذف میشود.
ب) در برخی موارد، از ضریب در تبدیل فوریه و انتگرال فوریه استفاده میشود. به صورت زیر:
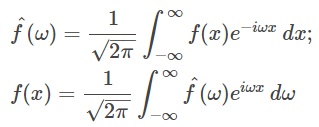
با تبدیل به میتوان از تبدیل فوریه به معکوس تبدیل فوریه رسید.
بنابراین قضیه پلانچرل به صورت زیر خواهد شد:
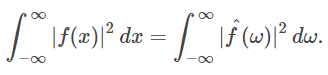
همانطور که بیان شد، با تبدیل به میتوان از تبدیل فوریه به معکوس تبدیل فوریه رسید. در این حالت تبدیل فوریه و معکوس تبدیل فوریه فرم متقارن دارند و هردو «عملگر یکانی» (Unitary Operators) هستند.
تبدیل فوریه و انتگرال سینوسی و کسینوسی
میتوان معادلات (۸) تا (۱0) را به شکل زیر نوشت:
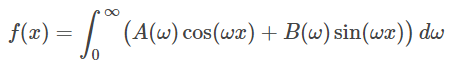
که در آن:
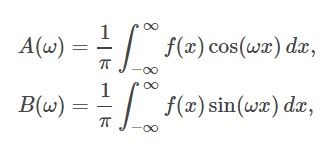
و:
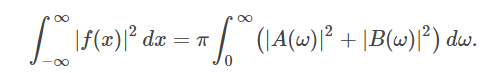
و به ترتیب تبدیلهای فوریه کسینوسی و سینوسی هستند.
نکته:
- اگر باشد، آنگاه تابع زوج است.
- اگر باشد، آنگاه تابع فرد است.
انتگرال فوریه کسینوسی
هر تابع در بازه را میتوان به فرم کسینوسی انتگرال فوریه تبدیل کرد:
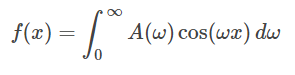
که در آن:
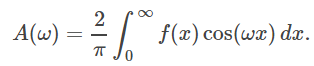
این معادلات به صورت زیر نیز نوشته میشوند:
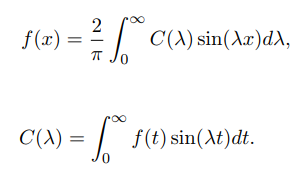
انتگرال فوریه سینوسی
هر تابع در بازه را میتوان به فرم سینوسی انتگرال فوریه تبدیل کرد:
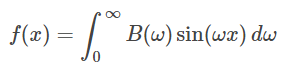
که در آن:
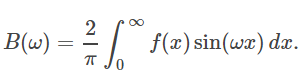
این معادلات به صورت زیر نیز نوشته میشوند:
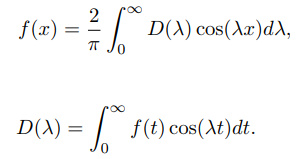
بنابراین، هر تابع در بازه را میتوان به صورت زیر نیز نوشت:
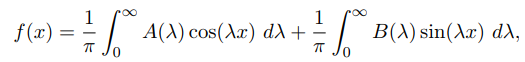
که در آن:
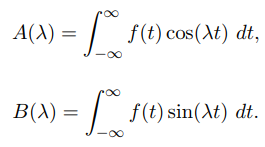
معادله (18) را میتوان به فرم زیر بازنویسی کرد:
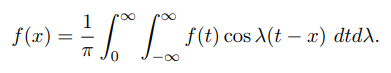
انتگرال فوریه مختلط
فرم مختلط انتگرال فوریه به صورت زیر داده میشود:
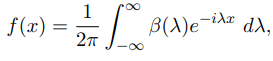
که در آن:
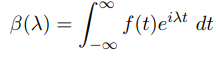
چند مثال از انتگرال فوریه
در ادامه به بررسی چند مثال از فرم انتگرالی سری فوریه و کاربرد آن در برخی انتگرالهای خاص پرداخته میشود.
مثال ۱
انتگرال فوریه تابع زیر را محاسبه کنید:
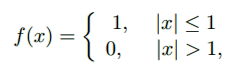
حال با استفاده از فرم انتگرالی فوریه این تابع، مقدار انتگرالهای زیر را بیابید:
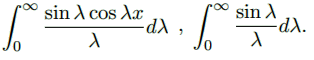
حل: طبق معادله (۲۲) میتوان نوشت:
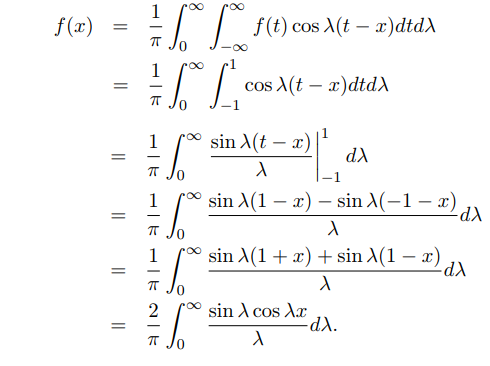
بنابراین:
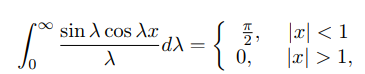
حال اگر را برابر صفر قرار دهیم، خواهیم داشت:
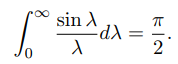
مثال ۲
انتگرال فوریه تابع زیر را بیابید:
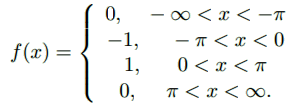
حل:
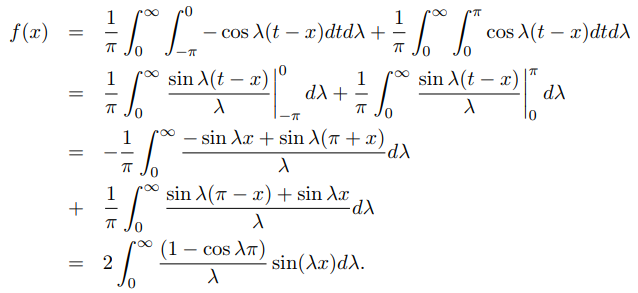
مثال ۳
انتگرال فوریه تابع زیر را بیابید:
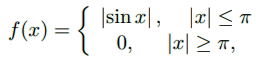
حال با استفاده از انتگرال فوریه تابع، رابطه زیر را اثبات کنید:
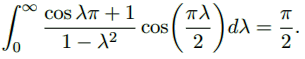
حل: مشاهده میشود که تابع در بازه ، یک تابع زوج است. بنابراین طبق معادله (۱۶)، داریم:
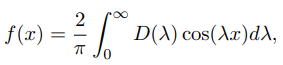
، طبق معادله (19) قابل محاسبه است. پس داریم:
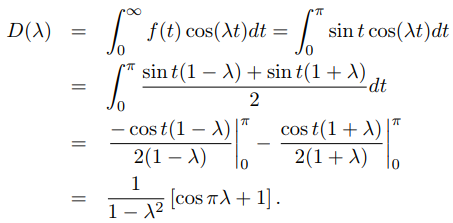
بنابراین داریم:
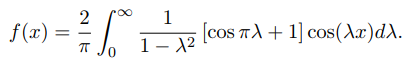
از آنجا که در کل بازه پیوسته است، انتگرال بالا به تابع همگرا میشود. با قرار دادن در تابع داریم:
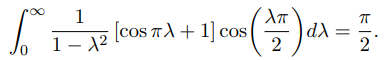
مثال ۴
فرم مختلط انتگرال فوریه زیر را بیابید:
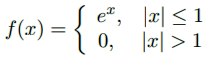
حل: طبق معادله (۲۳) داریم:
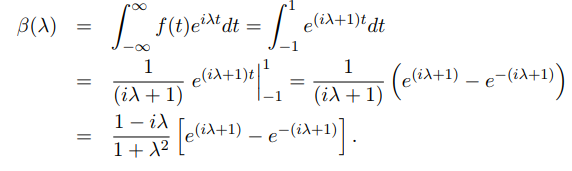
پس میتوان نوشت:

در صورتی که به مباحث مرتبط در زمینه ریاضیات علاقهمند هستید، آموزشهای زیر به شما پیشنهاد میشوند:
- سری فوریه (Fourier Series) — به زبان ساده
- سری فوریه سینوسی — به زبان ساده
- سری فوریه کسینوسی — به زبان ساده
- انتگرال و روش های محاسبه — به زبان ساده
- روشهای مشتقگیری — به همراه مثال
^^












سلام. خسته نباشید
نحوه دانلود ویدیو هارو توضیح بدید لطفا.زیر ویدیو مورد نظر که نوشته دانلود ویدیو میزنی هیچ اتفاقی نمی افته.مثلا من ریاضی-سری فوریه می خواستم.ایا پولیه؟
با سلام؛
اگر با کلیک روی لینکها، ویدیو دانلود نشد میتوانید با کلیک راست و کپی کردن لینک، آن را از طریق نرمافزاری مثل IDM دانلود کنید. ویدیوها درحالحاضر رایگان هستند.
با تشکر از همراهی شما با مجله فرادرس
بسیار سلیس و عالی. بعد از دیدن فیلمای مختلف و سورس خوندن بالاخره با تدریس شما این مطلب برام جا افتاد. دمتون گرم
خیلی ممنون به خاطر این آموزشها.
خداوند به شما خیر و برکت بدهد و توفیق روز افزون.
سلام. 3 دقیقه زمان مطالعه؟! بنظر اشتباه شده باشه بایستی 30 دقیقه زمان برای مطالعه این قسمت در نظر گرفت.
دمتون گرم
خیلی خوب بود
عالی بود. انتگرال رو خیلی خوب ساده سازی کردید.