در راستای ارائه مفاهیم مرتبط با انتگرال در این مطلب قصد داریم تا روشی را معرفی کنیم که در بدست آوردن انتگرال توابع رادیکالی مفید است. انتگرال به روش تغییر متغیر مثلثاتی تکنیکی شناخته شده در محاسبه انتگرال محسوب میشود. در حقیقت این روش، عکس محاسبه انتگرالگیری از توابع مثلثاتی است.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
توابع شامل a 2 − x 2 \large \sqrt { a ^ 2 − x ^ 2 } a 2 − x 2
در قسمت اول روش محاسبه انتگرال توابعی که عبارت a 2 − x 2 \sqrt { a ^ 2 − x ^ 2 } a 2 − x 2 ∫ 9 − x 2 d x \int \sqrt { 9 − x ^ 2 } d x ∫ 9 − x 2 d x
این انتگرال با استفاده از روشهایی مانند جزء به جزء قابل حل نیست. فرض کنید از تغییر متغیر x = 3 sin θ x = 3 \sin θ x = 3 sin θ d x = 3 cos θ d θ d x = 3 \cos θ \, d θ d x = 3 cos θ d θ
∫ 9 − x 2 d x = ∫ 9 − ( 3 sin θ ) 2 3 cos θ d θ \large ∫ \sqrt { 9− x ^ 2 } d x = ∫ \sqrt { 9 − ( 3 \sin θ ) ^ 2 } 3 \cos θ \, d θ ∫ 9 − x 2 d x = ∫ 9 − ( 3 sin θ ) 2 3 cos θ d θ
پس از سادهسازی عبارت بالا، میتوان آن را به صورت زیر بازنویسی کرد:
∫ 9 − x 2 d x = ∫ 9 1 − sin 2 θ cos θ d θ \large ∫ \sqrt { 9 − x ^ 2 } d x = ∫ 9 \sqrt { 1 − \sin ^ 2 θ } \cos θ \, d θ ∫ 9 − x 2 d x = ∫ 9 1 − sin 2 θ cos θ d θ
با استفاده از رابطه 1 − sin 2 θ = cos 2 θ 1 − \sin ^ 2 θ = \cos ^ 2 θ 1 − sin 2 θ = cos 2 θ
∫ 9 − x 2 d x = ∫ 9 cos 2 θ cos θ d θ \large ∫ \sqrt { 9 − x ^ 2 } d x = ∫ 9 \sqrt { \cos ^ 2 θ } \cos θ \, d θ ∫ 9 − x 2 d x = ∫ 9 cos 2 θ cos θ d θ
با فرض اینکه cos θ ≥ 0 \cos θ ≥ 0 cos θ ≥ 0
∫ 9 − x 2 d x = ∫ 9 cos 2 θ d θ \large ∫ \sqrt { 9 − x ^ 2 } d x = ∫ 9 \cos ^ 2 θ \, d θ ∫ 9 − x 2 d x = ∫ 9 cos 2 θ d θ
از این مرحله به بعد با استفاده از رابطه cos 2 θ = 1 + cos 2 θ 2 \cos ^ 2 θ = \frac { 1 + \cos 2 \theta } { 2 } cos 2 θ = 2 1 + cos 2 θ a 2 − x 2 \sqrt { a ^ 2 − x ^ 2 } a 2 − x 2 x = a sin θ x = a \sin \theta x = a sin θ لینک ارائه شده است.
مثال ۱
حاصل انتگرال زیر را بدست آورید.
∫ 1 x 4 9 − x 2 d x \large \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } ∫ x 4 9 − x 2 1 d x
در عبارت بالا ترم 9 − x 2 \sqrt { 9 - x ^ 2 } 9 − x 2
x = 3 sin θ d x = 3 cos θ d θ \large x = 3 \sin \theta \hspace {0.5in} \hspace {0.25in} d x = 3 \cos \theta \, d \theta x = 3 sin θ d x = 3 cos θ d θ
در نتیجه ترم رادیکالی موجود در تابع به صورت زیر در میآید.
9 − x 2 = 3 1 − sin 2 θ = 3 cos 2 θ = 3 ∣ cos θ ∣ = 3 cos θ \large \sqrt { 9 - { x ^ 2 } } = 3 \sqrt { 1 - { { \sin } ^ 2 } \theta } = 3 \sqrt { { { \cos } ^ 2 } \theta } = 3 \left | { \cos \theta } \right | = 3 \cos \theta 9 − x 2 = 3 1 − sin 2 θ = 3 cos 2 θ = 3 ∣ cos θ ∣ = 3 cos θ
دلیل حذف قدر مطلق این است که در اینجا هدف محاسبه انتگرال نامعین است. بنابراین با فرض مثبت بودن تمامی ترمها میتوان آن را حذف کرد. نهایتا شکل انتگرال را میتوان بر حسب θ، به صورت زیر بیان کرد:
∫ 1 x 4 9 − x 2 d x = ∫ 1 81 sin 4 θ ( 3 cos θ ) 3 cos θ d θ = 1 81 ∫ 1 sin 4 θ d θ = 1 81 ∫ csc 4 θ d θ \large \begin {align*} \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } & = \int { { \frac { 1 }{ { 8 1 { { \sin } ^ 4 } \theta \left ( { 3 \cos \theta } \right ) } } \, 3 \cos \theta \, d \theta } } \\ & = \frac { 1 } { { 8 1 } } \int { { \frac { 1 } { { { { \sin } ^ 4 } \theta } } \, d \theta } } \\ & = \frac { 1 } { { 8 1 } } \int { { { { \csc } ^ 4 } \theta \, d \theta } } \end {align*} ∫ x 4 9 − x 2 1 d x = ∫ 81 sin 4 θ ( 3 cos θ ) 1 3 cos θ d θ = 81 1 ∫ sin 4 θ 1 d θ = 81 1 ∫ csc 4 θ d θ
در مبحث انتگرال توابع مثلثاتی نحوه بدست آوردن توابع مثلثاتی را توضیح دادیم. به منظور محاسبه انتگرال فوق نیز میتوان از تغییر متغیر u = cot θ u = \cot \theta u = cot θ
∫ 1 x 4 9 − x 2 d x = 1 81 ∫ csc 2 θ csc 2 θ d θ = 1 81 ∫ ( cot 2 θ + 1 ) csc 2 θ d θ ⇒ u = cot θ = − 1 81 ∫ u 2 + 1 d u = − 1 81 ( 1 3 cot 3 θ + cot θ ) + c \large \begin {align*} \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } & = \frac { 1 } { { 8 1 } } \int { { { { \csc } ^ 2 } \theta \, { { \csc } ^ 2 } \theta \, d \theta } } \\ & = \frac { 1 } { { 8 1 } } \int { { \left ( { { { \cot } ^ 2 } \theta + 1 } \right ) \, { { \csc } ^ 2 } \theta \, d \theta } } \hspace {0.5in} \Rightarrow \ \ u = \cot \theta \\ & = - \frac { 1 } { { 8 1 } } \int { { { u ^ 2 } + 1 \, d u } } \\ & = - \frac { 1 } { { 8 1 } } \left ( { \frac { 1 } { 3 } { { \cot } ^ 3 } \theta + \cot \theta } \right ) + c \end{align*} ∫ x 4 9 − x 2 1 d x = 81 1 ∫ csc 2 θ csc 2 θ d θ = 81 1 ∫ ( cot 2 θ + 1 ) csc 2 θ d θ ⇒ u = cot θ = − 81 1 ∫ u 2 + 1 d u = − 81 1 ( 3 1 cot 3 θ + cot θ ) + c
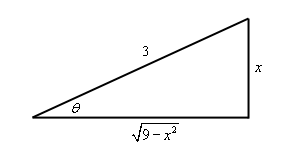
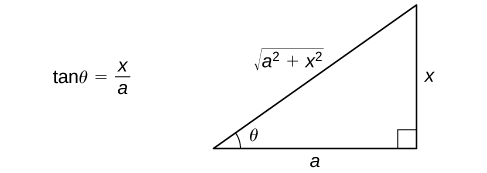
به منظور محاسبه cot θ، میتوان از مثلث زیر استفاده کرد. با توجه به تغییر متغیر در نظر گرفته شده، میتوان مثلث زیر را تصور کرد.
با توجه به مثلث فوق روابط زیر برقرارند.
sin θ = x 3 cot θ = 9 − x 2 x \large \sin \theta = \frac { x } { 3 } \hspace {0.5in} \cot \theta = \frac { { \sqrt { 9 - { x ^ 2 } } } } { x } sin θ = 3 x cot θ = x 9 − x 2
نهایتا حاصل انتگرال برابر با عبارت زیر بدست میآید.
∫ 1 x 4 9 − x 2 d x = − 1 81 ( 1 3 ( 9 − x 2 x ) 3 + 9 − x 2 x ) + c = − ( 9 − x 2 ) 3 2 243 x 3 − 9 − x 2 81 x + c \large \begin {align*} \int { { \frac { 1 } { { { x ^ 4 } \sqrt { 9 - { x ^ 2 } } } } \, d x } } & = - \frac { 1 } { { 8 1 } } \left ( { \frac { 1 } { 3 } { { \left ( { \frac { { \sqrt { 9 - { x ^ 2 } } } } { x } } \right ) } ^ 3 } + \frac { { \sqrt { 9 - { x ^ 2 } } } } { x } } \right ) + c \\ & = - \frac { { { { \left ( { 9 - { x ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } }{ { 2 4 3 { x ^ 3 } } } - \frac { { \sqrt { 9 - { x ^ 2 } } } } { { 8 1 x } } + c \end {align*} ∫ x 4 9 − x 2 1 d x = − 81 1 3 1 ( x 9 − x 2 ) 3 + x 9 − x 2 + c = − 243 x 3 ( 9 − x 2 ) 2 3 − 81 x 9 − x 2 + c
در برخی از موارد ممکن است، به جای x از عبارت ax+b استفاده شده باشد. در چنین مواردی در ابتدا بایستی عبارت زیر رادیکال را ساده کرد.
مثال ۲
حاصل انتگرال زیر را بدست آورید.
∫ ( z + 3 ) 5 ( 40 − 6 z − z 2 ) 3 2 d z \large \displaystyle \int { { \frac { { { { \left ( { z + 3 } \right ) } ^ 5 } } } { { { { \left ( { 4 0 - 6 z - { z ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d z } } ∫ ( 40 − 6 z − z 2 ) 2 3 ( z + 3 ) 5 d z
اولین قدمی که بایستی انجام شود، مربعی کردن عبارت زیر انتگرال است. در حقیقت عبارت تحت انتگرال را میتوان به صورت زیر بیان کرد:
40 − 6 z − z 2 = − ( z 2 + 6 z − 40 ) = − ( z 2 + 6 z + 9 − 9 − 40 ) = − [ ( z + 3 ) 2 − 49 ] = 49 − ( z + 3 ) 2 \large \begin {align*} 4 0 - 6 z - { z ^ 2 } & = - \left ( { { z ^ 2 } + 6 z - 4 0 } \right ) = - \left ( { { z ^ 2 } + 6 z + 9 - 9 - 4 0 } \right ) = - \left [ { { { \left ( { z + 3 } \right ) } ^ 2 } - 4 9 } \right ] \\ & = 4 9 - { \left ( { z + 3 } \right ) ^ 2 } \end {align*} 40 − 6 z − z 2 = − ( z 2 + 6 z − 40 ) = − ( z 2 + 6 z + 9 − 9 − 40 ) = − [ ( z + 3 ) 2 − 49 ] = 49 − ( z + 3 ) 2
با استفاده از عبارت فوق، رابطه انتگرال به شکل زیر در میآید.
∫ ( z + 3 ) 5 ( 40 − 6 z − z 2 ) 3 2 d z = ∫ ( z + 3 ) 5 ( 49 − ( z + 3 ) 2 ) 3 2 d z \large \int { { \frac { { { { \left ( { z + 3 } \right ) } ^ 5 } } } { { { { \left ( { 4 0 - 6 z - { z ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d z } } = \int { { \frac { { { { \left ( { z + 3 } \right ) } ^ 5 } } } { { { { \left ( { 4 9 - { { \left ( { z + 3 } \right ) } ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d z } } ∫ ( 40 − 6 z − z 2 ) 2 3 ( z + 3 ) 5 d z = ∫ ( 49 − ( z + 3 ) 2 ) 2 3 ( z + 3 ) 5 d z
عبارت 49 − ( z + 3 ) 2 4 9 - ( z + 3 ) ^2 49 − ( z + 3 ) 2 ( a 2 − x 2 ) ( a ^ 2 - x ^ 2 ) ( a 2 − x 2 )
z + 3 = 7 sin ( θ ) \large z + 3 = 7 \sin \left ( \theta \right ) z + 3 = 7 sin ( θ )
با این تغییر، عبارت زیر انتگرال نیز به شکل زیر در خواهد آمد.
( 49 − ( z + 3 ) 2 ) 3 2 = [ 49 − ( z + 3 ) ] 3 = [ 49 − 49 sin 2 ( θ ) ] 3 = [ 7 cos 2 ( θ ) ] 3 = 343 ∣ cos ( θ ) ∣ 3 { \left ( { 4 9 - { { \left ( { z + 3 } \right ) } ^ 2 } } \right ) ^ { \frac { 3 } { 2 } } } = { \left [ { \sqrt { 4 9 - \left ( { z + 3 } \right ) } } \right ] ^ 3 } = { \left [ { \sqrt { 4 9 - 4 9 { { \sin } ^ 2 } \left ( \theta \right ) } } \right ] ^ 3 } = { \left [ { 7 \sqrt { { { \cos } ^ 2 } \left ( \theta \right ) } } \right ] ^ 3 } = 3 4 3 { \left| { \cos \left ( \theta \right ) } \right | ^ 3 } ( 49 − ( z + 3 ) 2 ) 2 3 = [ 49 − ( z + 3 ) ] 3 = [ 49 − 49 sin 2 ( θ ) ] 3 = [ 7 cos 2 ( θ ) ] 3 = 343 ∣ cos ( θ ) ∣ 3
در ادامه با توجه به این که انتگرال گرفته شده، به صورت نامعین است، کسینوس مثبت فرض شده و میتوان آن را از قدر مطلق بیرون آورد. نهایتا عبارت فوق به صورت زیر بازنویسی میشود.
( 49 − ( z + 3 ) 2 ) 3 2 = 343 cos 3 ( θ ) \large { \left ( { 4 9 - { { \left ( { z + 3 } \right ) } ^ 2 } } \right ) ^ { \frac { 3 } { 2 } } } = 3 4 3 { \cos ^ 3 } \left ( \theta \right ) ( 49 − ( z + 3 ) 2 ) 2 3 = 343 cos 3 ( θ )
همچنین دیفرانسیلِ متناسب با تغییر متغیر در نظر گرفته شده، برابر است با:
( 1 ) d z = 7 cos ( θ ) d θ ⇒ d z = 7 cos ( θ ) d θ \large \left ( 1 \right ) d z = 7 \cos \left ( \theta \right ) \, d \theta \hspace {0.25in} \hspace {0.25in} \Rightarrow \hspace {0.25in} \hspace {0.25in} d z = 7 \cos \left ( \theta \right) \, d \theta ( 1 ) d z = 7 cos ( θ ) d θ ⇒ d z = 7 cos ( θ ) d θ
با جایگذاری تغییر متغیر مذکور به جای z، انتگرال به صورت زیر در میآید.
∫ ( z + 3 ) 5 ( 40 − 6 z − z 2 ) 3 2 d z = ∫ 16807 sin 5 ( θ ) 343 cos 3 ( θ ) ( 7 cos ( θ ) ) d θ = 343 ∫ sin 5 ( θ ) cos 2 ( θ ) d θ \large \int { { \frac { { { { \left ( { z + 3 } \right ) } ^ 5 } } } { { { { \left ( { 4 0 - 6 z - { z ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d z } } = \int { { \frac { { 1 6 8 0 7 { { \sin } ^ 5 } \left ( \theta \right ) } }{ { 3 4 3 { { \cos } ^ 3 } \left ( \theta \right ) } } \left ( { 7 \cos \left ( \theta \right ) } \right ) \, d \theta } } = 3 4 3 \int { { \frac { { { { \sin } ^ 5 } \left ( \theta \right ) } } { { { { \cos } ^ 2 } \left ( \theta \right ) } } \, d \theta } } ∫ ( 40 − 6 z − z 2 ) 2 3 ( z + 3 ) 5 d z = ∫ 343 cos 3 ( θ ) 16807 sin 5 ( θ ) ( 7 cos ( θ ) ) d θ = 343 ∫ cos 2 ( θ ) sin 5 ( θ ) d θ
برای حل این انتگرال، یک توان از sin θ \sin \theta sin θ cos θ \cos \theta cos θ u = cos θ u = \cos \theta u = cos θ
∫ ( z + 3 ) 5 ( 40 − 6 z − z 2 ) 3 2 d z = 343 ∫ [ 1 − cos 2 ( θ ) ] 2 cos 2 ( θ ) sin ( θ ) d θ ⇒ u = cos ( θ ) = − 343 ∫ [ 1 − u 2 ] 2 u 2 d u = − 343 ∫ u − 2 − 2 + u 2 d u = − 343 ( − u − 1 − 2 u + 1 3 u 3 ) + c = − 343 ( − 1 cos ( θ ) − 2 cos ( θ ) + 1 3 cos 3 ( θ ) ) + c \large \begin {align*} \int { { \frac { { { { \left ( { z + 3 } \right ) } ^ 5 } } } { { { { \left ( { 4 0 - 6 z - { z ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d z } } & = 3 4 3 \int { { \frac { { { { \left [ { 1 - { { \cos } ^ 2 } \left ( \theta \right ) } \right ] } ^ 2 } } } { { { { \cos } ^ 2 } \left ( \theta \right ) } } \sin \left ( \theta \right ) \, d \theta } } \hspace {0.25in} \hspace {0.25in} \Rightarrow u = \cos \left ( \theta \right) \\ & = - 3 4 3 \int { { \frac { { { { \left [ { 1 - { u ^ 2 } } \right ] } ^ 2 } } } { { { u ^ 2 } } } \, d u } } = - 3 4 3 \int { { { u ^ { - 2 } } - 2 + { u ^ 2 } \, d u } } \\ & = - 3 4 3 \left ( { - {u ^ { - 1 } } - 2 u + \frac { 1 } { 3 } { u ^ 3 } } \right ) + c\\ & = - 3 4 3 \left( { - \frac{1}{{\cos \left( \theta \right)}} - 2\cos \left( \theta \right) + \frac{ 1 } { 3 } { { \cos } ^ 3 } \left ( \theta \right ) } \right ) + c \end {align*} ∫ ( 40 − 6 z − z 2 ) 2 3 ( z + 3 ) 5 d z = 343 ∫ cos 2 ( θ ) [ 1 − cos 2 ( θ ) ] 2 sin ( θ ) d θ ⇒ u = cos ( θ ) = − 343 ∫ u 2 [ 1 − u 2 ] 2 d u = − 343 ∫ u − 2 − 2 + u 2 d u = − 343 ( − u − 1 − 2 u + 3 1 u 3 ) + c = − 343 ( − cos ( θ ) 1 − 2 cos ( θ ) + 3 1 cos 3 ( θ ) ) + c
از طرفی با توجه به تغییر متغیر در نظر گرفته شده، میتوان از مثلث زیر برای محاسبه نسبتهای مثلثاتی بهره برد.
با توجه به مثلث فوق، cos θ \cos \theta cos θ
cos ( θ ) = 49 − ( z + 3 ) 2 7 \large \cos \left ( \theta \right ) = \frac { { \sqrt { 4 9 - { { \left ( { z + 3 } \right ) } ^ 2 } } } } { 7 } cos ( θ ) = 7 49 − ( z + 3 ) 2
بنابراین حاصل انتگرال برابر است با:
∫ ( z + 3 ) 5 ( 40 − 6 z − z 2 ) 3 2 d z = 2401 49 − ( z + 3 ) 2 + 98 49 − ( z + 3 ) 2 − ( 49 − ( z + 3 ) 2 ) 3 2 3 + c \large \int { { \frac { { { { \left ( { z + 3 } \right ) } ^ 5 } } } { { { { \left ( { 40 - 6 z - { z ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d z } } = { { \frac { { 2401 } } { { \sqrt { 49 - { { \left ( { z + 3 } \right ) } ^ 2 } } } } + 98 \sqrt { 49 - { { \left ( { z + 3 } \right ) } ^ 2 } } - \frac { { { { \left( { 49 - { { \left( { z + 3 } \right ) } ^ 2 } } \right ) } ^ { \frac { 3 } { 2 } } } } } { 3 } + c } } ∫ ( 40 − 6 z − z 2 ) 2 3 ( z + 3 ) 5 d z = 49 − ( z + 3 ) 2 2401 + 98 49 − ( z + 3 ) 2 − 3 ( 49 − ( z + 3 ) 2 ) 2 3 + c
توابع شامل a 2 + x 2 \large \sqrt { a ^ 2 + x ^ 2 } a 2 + x 2
برای توابعی که ترم a 2 + x 2 \large \sqrt { a ^ 2 + x ^ 2 } a 2 + x 2 x = a tan θ x = a \tan θ x = a tan θ
مثال ۳
حاصل انتگرال زیر را بیابید.
∫ 0 1 6 x 5 ( 36 x 2 + 1 ) 3 2 d x \large \int _ { { \, 0 } } ^ { { \, \frac { 1 } { 6 } } } { { \frac { { { x ^ 5 } } } { { { { \left ( { 3 6 { x ^ 2 } + 1 } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d x } } ∫ 0 6 1 ( 36 x 2 + 1 ) 2 3 x 5 d x
تابع تحت انتگرال برای این تابع را میتوان به صورت زیر در نظر گرفت.
( 36 x 2 + 1 ) 3 2 = ( ( 36 x 2 + 1 ) 1 2 ) 3 = ( 36 x 2 + 1 ) 3 \large {\left( {36{x^2} + 1} \right)^{\frac{3}{2}}} = {\left( {{{\left( {36{x^2} + 1} \right)}^{\frac{1}{2}}}} \right)^3} = {\left( {\sqrt {36{x^2} + 1} } \right)^3} ( 36 x 2 + 1 ) 2 3 = ( ( 36 x 2 + 1 ) 2 1 ) 3 = ( 36 x 2 + 1 ) 3
با فاکتورگیری از ضریب x، میتوان به قالبِ a 2 + x 2 \sqrt { a ^ 2 + x ^ 2 } a 2 + x 2
x = 1 6 tan θ d x = 1 6 sec 2 θ d θ \large x = \frac { 1 } { 6 } \tan \theta \hspace {0.5in} \hspace {0.25in} d x = \frac { 1 } { 6 } { \sec ^ 2 } \theta \, d \theta x = 6 1 tan θ d x = 6 1 sec 2 θ d θ
با استفاده از تغییر متغیر فوق، مخرج کسرِ انتگرال به صورت زیر در میآید.
( 36 x 2 + 1 ) 3 = ( tan 2 θ + 1 ) 3 = ( sec 2 θ ) 3 = ∣ sec θ ∣ 3 \large { \left ( { \sqrt { 3 6 { x ^ 2 } + 1 } } \right ) ^ 3 } = { \left ( { \sqrt { { { \tan } ^ 2 } \theta + 1 } } \right ) ^ 3 } = { \left ( { \sqrt { { { \sec } ^ 2 } \theta } } \right ) ^ 3 } = { \left| { \sec \theta } \right| ^ 3 } ( 36 x 2 + 1 ) 3 = ( tan 2 θ + 1 ) 3 = ( sec 2 θ ) 3 = ∣ sec θ ∣ 3
توجه داشته باشید که بازههای قرار داده شده، برای x هستند. بنابراین در هنگام تغییر متغیر باید آنها را بر حسب متغیر جدید بیان کرد. از این رو بازهی جدید را میتوان بهصورت زیر بدست آورد.
x = 0 : 0 = 1 6 tan θ ⇒ θ = tan − 1 ( 0 ) = 0 x = 1 6 : 1 6 = 1 6 tan θ ⇒ θ = tan − 1 ( 1 ) = π 4 \large \begin {align*} x & = 0 \, \, \, :\, \, \, 0 = \frac { 1 } { 6 } \tan \theta \hspace {0.25in} \, \, \, \Rightarrow \hspace {0.25in} \, \, \theta = { \tan ^ { - 1} } \left ( 0 \right ) = 0 \\ x &= \frac { 1 }{ 6 } \, \, \, :\, \, \, \frac { 1 } { 6 } = \frac { 1 } { 6 } \tan \theta \hspace {0.25in} \, \Rightarrow \hspace {0.25in} \, \, \theta = {\tan ^{ - 1}}\left( 1 \right) = \frac { \pi } { 4 } \end {align*} x x = 0 : 0 = 6 1 tan θ ⇒ θ = tan − 1 ( 0 ) = 0 = 6 1 : 6 1 = 6 1 tan θ ⇒ θ = tan − 1 ( 1 ) = 4 π
با استفاده از تغییر متغیر در نظر گرفته شده، تابع تحت انتگرال را میتوان بر حسب متغیر جدید به صورت زیر نوشت:
∫ 0 1 6 x 5 ( 36 x 2 + 1 ) 3 2 d x = 1 46656 ∫ 0 π 4 sin 5 θ cos 4 θ d θ = 1 46656 ∫ 0 π 4 ( 1 − cos 2 θ ) 2 cos 4 θ sin θ d θ \large \begin {align*} \int _ { { \, 0 } } ^ { { \, \frac { 1 } { 6 } } } { { \frac { { { x ^ 5 } } } { {{ { \left( { 3 6 { x ^ 2 } + 1 } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d x } } & = \frac{1}{{46656}}\int_{{\,0}}^{{\,\frac{\pi }{4}}}{{\frac{{{{\sin }^5}\theta }}{{{{\cos }^4}\theta }}d\theta }}\\ & = \frac{1}{{46656}}\int_{{\,0}}^{{\,\frac{\pi }{4}}}{{\frac{{{{\left( {1 - {{\cos }^2}\theta } \right)}^2}}}{{{{\cos }^4}\theta }}\sin \theta d\theta }}\end{align*} ∫ 0 6 1 ( 36 x 2 + 1 ) 2 3 x 5 d x = 46656 1 ∫ 0 4 π cos 4 θ sin 5 θ d θ = 46656 1 ∫ 0 4 π cos 4 θ ( 1 − cos 2 θ ) 2 sin θ d θ
همانند مثال قبل، تمامی عبارت زیر انتگرال را بر حسب cos θ \cos \theta cos θ sin θ \sin \theta sin θ
∫ 0 1 6 x 5 ( 36 x 2 + 1 ) 3 2 d x = 1 46656 ∫ 0 π 4 sin 5 θ cos 4 θ d θ = 1 46656 ∫ 0 π 4 ( 1 − cos 2 θ ) 2 cos 4 θ sin θ d θ \large \begin {align*} \int _ { { \, 0 } } ^ { { \, \frac { 1 } { 6 } } } { { \frac { { { x ^ 5 } } } { { { { \left( { 3 6 { x ^ 2 } + 1} \right ) } ^{ \frac { 3 } { 2 }} } } } \, d x } } & = \frac { 1 } { { 4 6 6 5 6 } } \int _ { {\, 0 } } ^ { { \, \frac{\pi }{4}}}{{\frac{{{{\sin }^5}\theta }}{{{{\cos }^4}\theta }}d\theta }}\\ & = \frac{1}{{46656}}\int_{{\,0}}^{{\,\frac{\pi }{4} } } { { \frac { { { { \left ( { 1 - { { \cos } ^ 2 } \theta } \right ) } ^ 2 } } } { { { { \cos } ^ 4 } \theta } } \sin \theta d\theta } } \end {align*} ∫ 0 6 1 ( 36 x 2 + 1 ) 2 3 x 5 d x = 46656 1 ∫ 0 4 π cos 4 θ sin 5 θ d θ = 46656 1 ∫ 0 4 π cos 4 θ ( 1 − cos 2 θ ) 2 sin θ d θ
حال بایستی از تغییر متغیر u = cos θ u = \cos \theta u = cos θ
θ = 0 ⇒ u = cos 0 = 1 θ = π 4 ⇒ u = cos π 4 = 2 2 \large \begin {align*}\theta & = 0 & \Rightarrow \hspace{0.75in} & u = \cos 0 = 1\\ \theta & = \frac { \pi } { 4 } & \Rightarrow \hspace{0.75in} & u = \cos \frac { \pi } { 4 } = \frac { { \sqrt 2 } }{ 2 } \end {align*} θ θ = 0 = 4 π ⇒ ⇒ u = cos 0 = 1 u = cos 4 π = 2 2
بنابراین نهایتا حاصل انتگرال برابر میشود با:
∫ 0 1 6 x 5 ( 36 x 2 + 1 ) 3 2 d x = − 1 46656 ∫ 1 2 2 u − 4 − 2 u − 2 + 1 d u = − 1 46656 ( − 1 3 u 3 + 2 u + u ) ∣ 1 2 2 = 1 17496 − 11 2 279936 \large \begin {align*} \int _ { { \, 0 } } ^ { { \, \frac { 1 } { 6 } } } { { \frac { { { x ^ 5 } } } { { { { \left( { 3 6 { x ^ 2 } + 1 } \right ) } ^ { \frac { 3 } { 2 } } } } } \, d x } } & = - \frac { 1 }{ {4 6656 } } \int _ { { \, 1 } } ^ { { \, \frac { { \sqrt 2 } } { 2 } } } { { { u ^ { - 4 } } - 2 { u ^ { - 2 } } + 1 \, d u } } \\ & = - \frac{1}{{46656}}\left. {\left( { - \frac { 1 } { { 3 { u ^ 3 } } } + \frac { 2 } { u } + u} \right)} \right|_1^{\frac{{\sqrt 2 }}{2}}\\ & = \frac{1}{{17496}} - \frac{{11\sqrt 2 }}{{279936}}\end{align*} ∫ 0 6 1 ( 36 x 2 + 1 ) 2 3 x 5 d x = − 46656 1 ∫ 1 2 2 u − 4 − 2 u − 2 + 1 d u = − 46656 1 ( − 3 u 3 1 + u 2 + u ) 1 2 2 = 17496 1 − 279936 11 2
توابع شامل x 2 − a 2 \large \sqrt { x ^ 2 - a ^ 2 } x 2 − a 2
به منظور حل توابعی به شکل x 2 − a 2 \large \sqrt { x ^ 2 - a ^ 2 } x 2 − a 2 x = a sec θ x = a \sec θ x = a sec θ
با استفاده از این تغییر متغیر، d x = a sec θ tan θ d θ d x = a \secθ \tan θ \, dθ d x = a sec θ tan θ d θ
x 2 − a 2 = ( a sec θ ) 2 − a 2 = a 2 ( sec 2 θ − 1 ) = a 2 tan 2 θ = ∣ a tan θ ∣ \large \sqrt { x ^ 2−a ^ 2 } = \sqrt { ( a \secθ) ^ 2− a ^ 2 } = \sqrt { a ^ 2 (\sec ^ 2 θ - 1 ) } = \sqrt { a ^ 2 \tan ^ 2 θ }= |a \tan θ| x 2 − a 2 = ( a sec θ ) 2 − a 2 = a 2 ( sec 2 θ − 1 ) = a 2 tan 2 θ = ∣ a tan θ ∣
توجه داشته باشید که رابطه فوق در x>a برابر با a tan θ a \tan \theta a tan θ − a tan θ - a \tan \theta − a tan θ
مثال ۴
حاصل انتگرال زیر را بیابید.
∫ x 2 x 2 − 4 x − 7 d x \large \int { { \frac { x } { { \sqrt { 2 { x ^ 2 } - 4 x - 7 } } } \, d x } } ∫ 2 x 2 − 4 x − 7 x d x
در ظاهر عبارت زیر رادیکال به نظر یک چند جملهای از مرتبه دو میرسد. اما میتوان آن را به شکل مربع کامل نوشته و نهایتا از تغییر متغیر مثلثاتی استفاده کرد. در ابتدا عبارت زیر رادیکال را به صورت زیر بازنویسی میکنیم.
2 ( x 2 − 2 x − 7 2 ) = 2 ( x 2 − 2 x + 1 − 1 − 7 2 ) = 2 ( ( x − 1 ) 2 − 9 2 ) = 2 ( x − 1 ) 2 − 9 \large 2 \left ( {{ x ^ 2 } - 2 x - \frac { 7 } { 2 } } \right ) = 2 \left ( { { x ^ 2 } - 2 x + 1 - 1 - \frac { 7 } { 2 } } \right ) = 2 \left ( { { { \left ( { x - 1 } \right ) } ^ 2 } - \frac { 9 } { 2 } } \right ) = 2 { \left ( { x - 1 } \right ) ^ 2 } - 9 2 ( x 2 − 2 x − 2 7 ) = 2 ( x 2 − 2 x + 1 − 1 − 2 7 ) = 2 ( ( x − 1 ) 2 − 2 9 ) = 2 ( x − 1 ) 2 − 9
بنابراین عبارت رادیکالی به شکل زیر در میآید.
2 x 2 − 4 x − 7 = 2 ( x − 1 ) 2 − 9 \large \sqrt { 2 { x ^ 2 } - 4 x - 7 } = \sqrt { 2 { { \left ( { x - 1 } \right ) } ^ 2 } - 9 } 2 x 2 − 4 x − 7 = 2 ( x − 1 ) 2 − 9
با توجه به رابطه فوق بایستی از تغییر متغیر زیر استفاده کرد.
x − 1 = 3 2 sec θ ⇒ x = 1 + 3 2 sec θ , d x = 3 2 sec θ tan θ d θ \large x - 1 = \frac { 3 } { { \sqrt 2 } } \sec \theta \Rightarrow \hspace {0.25in} x = 1 + \frac { 3 } { { \sqrt 2 } } \sec \theta \hspace {0.25in} , d x = \frac { 3 } { { \sqrt 2 } } \sec \theta \tan \theta \, d \theta x − 1 = 2 3 sec θ ⇒ x = 1 + 2 3 sec θ , d x = 2 3 sec θ tan θ d θ
با این تغییر متغیر، عبارت رادیکالی به صورت زیر بر حسب تانژانت بدست میآید.
2 x 2 − 4 x − 7 = 2 ( x − 1 ) 2 − 9 = 9 sec 2 θ − 9 = 3 tan 2 θ = 3 ∣ tan θ ∣ = 3 tan θ \large \sqrt {2{x^2} - 4x - 7} = \sqrt {2{{\left( {x - 1} \right)}^2} - 9} = \sqrt {9{{\sec }^2}\theta - 9} = 3\sqrt {{{\tan }^2}\theta } = 3\left| {\tan \theta } \right| = 3\tan \theta 2 x 2 − 4 x − 7 = 2 ( x − 1 ) 2 − 9 = 9 sec 2 θ − 9 = 3 tan 2 θ = 3 ∣ tan θ ∣ = 3 tan θ
توجه داشته باشید که انتگرالگیری به صورت نامعین است، لذا نیازی به استفاده از قدرمطلق نیست. بنابراین نهایتا حاصل انتگرال را میتوان بهصورت زیر بیان کرد:
∫ x 2 x 2 − 4 x − 7 d x = ∫ 1 + 3 2 sec θ 3 tan θ ( 3 2 sec θ tan θ ) d θ = ∫ 1 2 sec θ + 3 2 sec 2 θ d θ = 1 2 ln ∣ sec θ + tan θ ∣ + 3 2 tan θ + c \large \begin {align*} \int { { \frac { x } { { \sqrt { 2 { x ^ 2 } - 4 x - 7 } } } \, d x } } & = \int { { \frac{ { 1 + \frac { 3 } { { \sqrt 2 } } \sec \theta } } { { 3 \tan \theta } } \left( {\frac { 3 } { { \sqrt 2 } } \sec \theta \tan \theta } \right)\,d\theta } } \\ & = \int { { \frac { 1 } { { \sqrt 2 } } \sec \theta + \frac { 3 } { 2 } { { \sec } ^ 2 } \theta \, d \theta } } \\ & = \frac { 1 } { { \sqrt 2 } } \ln \left| {\sec \theta + \tan \theta } \right| + \frac{3}{2}\tan \theta + c\end{align*} ∫ 2 x 2 − 4 x − 7 x d x = ∫ 3 tan θ 1 + 2 3 sec θ ( 2 3 sec θ tan θ ) d θ = ∫ 2 1 sec θ + 2 3 sec 2 θ d θ = 2 1 ln ∣ sec θ + tan θ ∣ + 2 3 tan θ + c
برای بدست آوردن عبارت مثلثاتی فوق، راحتتر آن است که در ابتدا مثلث مربوط به تغییر متغیر در نظر گرفته شده، ترسیم شود. در ادامه این مثلث ارائه شده.
با توجه به مثلث فوق، توابع سکانت و تانژانت برابرند با:
sec θ = 2 ( x − 1 ) 3 , tan θ = 2 x 2 − 4 x − 7 3 \large \sec \theta = \frac { { \sqrt 2 \left ( { x - 1 } \right ) } } { 3 } , \ \tan \theta = \frac { { \sqrt { 2 { x ^ 2 } - 4 x - 7 } } } { 3 } sec θ = 3 2 ( x − 1 ) , tan θ = 3 2 x 2 − 4 x − 7
بنابراین نهایتا حاصل انتگرال برابر میشود با:
∫ x 2 x 2 − 4 x − 7 d x = 1 2 ln ∣ 2 ( x − 1 ) 3 + 2 x 2 − 4 x − 7 3 ∣ + 2 x 2 − 4 x − 7 2 + c \large \int{{\frac{x}{{\sqrt {2{x^2} - 4x - 7} }}\,dx}} = \frac{1}{{\sqrt 2 }}\ln \left| {\frac{{\sqrt 2 \left( {x - 1} \right)}}{3} + \frac{{\sqrt {2{x^2} - 4x - 7} }}{3}} \right| + \frac{{\sqrt {2{x^2} - 4x - 7} }}{2} + c ∫ 2 x 2 − 4 x − 7 x d x = 2 1 ln 3 2 ( x − 1 ) + 3 2 x 2 − 4 x − 7 + 2 2 x 2 − 4 x − 7 + c
خلاصه
حاصل انتگرال توابعی که عبارت a 2 − x 2 \sqrt{a^2−x^2} a 2 − x 2 x = a sin θ x=a\sin θ x = a sin θ
در انتگرالهایی که عبارت a 2 + x 2 \sqrt{a^2+x^2} a 2 + x 2 x = a tan θ x=a\tan θ x = a tan θ
به منظور بدست آوردن انتگرال توابعی که عبارتی به شکلِ x 2 − a 2 \sqrt{x^2−a^2} x 2 − a 2 x = a sec θ x = a \sec θ x = a sec θ
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^
فیلم های آموزش انتگرال به روش تغییر متغیر مثلثاتی – به زبان ساده (+ دانلود فیلم آموزش گام به گام) فیلم آموزشی حل انتگرالهای $$sqrt{a^2 -x ^ 2}$$ فیلم آموزشی حل انتگرالهای $$sqrt{a^2 +x ^ 2}$$ فیلم آموزشی حل انتگرالهای $$sqrt{x^2 -a ^ 2}$$ 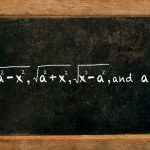
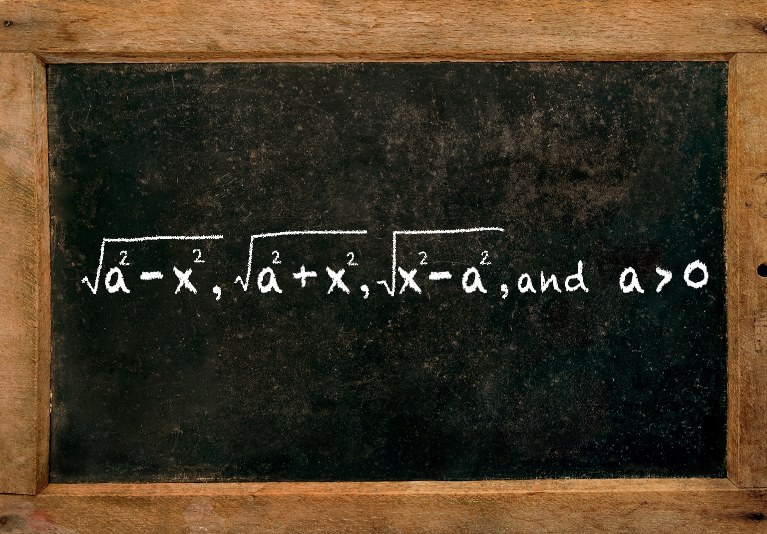
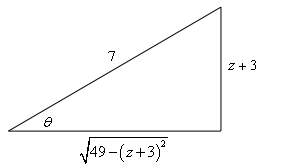
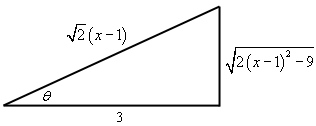













سلام وقتی شما تغییر متغیر انجام میدهید و برفرض به قدرمطلق cosx میرسید چرا آن را مثبت فرض میکنید، اگر منفی فرض کنیم چه میشود؟
کارتون خیلی درسته . خدا خیرتون بده