آزمون گلدفلد و کوانت (Goldfeld–Quandt Test) – به زبان ساده
در تحلیل رگرسیون خطی (Linear Regression)، یکی از شرایط مهم، داشتن خاصیت همواریانسی (Homoscedasticity) است. در صورتی که مدل استخراج شده از نمونه تصادفی، چنین خاصیتی نداشته باشد، امکان استفاده از آن محدود شده و ممکن است نتایج پیشبینی با خطای زیاد همراه باشند. آزمون گلدفلد و کوانت (Goldfeld-Quandt Test) یکی از روشهایی است که برای سنجش خاصیت همواریانسی مدل رگرسیونی به کار میرود. در این نوشتار به بررسی آماره و آزمون گلدفلد و کوانت پرداخته و با استفاده از مثالهای کاربردی با زبان برنامهنویسی R، با آن بیشتر آشنا میشویم.

به منظور آگاهی نسبت به رگرسیون خطی چندگانه نوشتار رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده را بخوانید. همچنین خواندن هم خطی در مدل رگرسیونی — به زبان ساده نیز خالی از لطف نیست.
آزمون گلدفلد و کوانت (Goldfeld-Quandt Test)
در مبحث رگرسیون چندگانه (Multiple Regression) و حتی رگرسیون خطی ساده (Univariate Regression)، یکی از فرضهایی که باید مورد آزمون قرار گیرد، ثابت بودن واریانس جمله خطا است. ولی ممکن است واریانس عبارت خطا یا متغیر وابسته، به یک یا چند متغیر مستقل بستگی داشته باشد و با افزایش مقدار ها، واریانس نیز دچار تغییر شود.
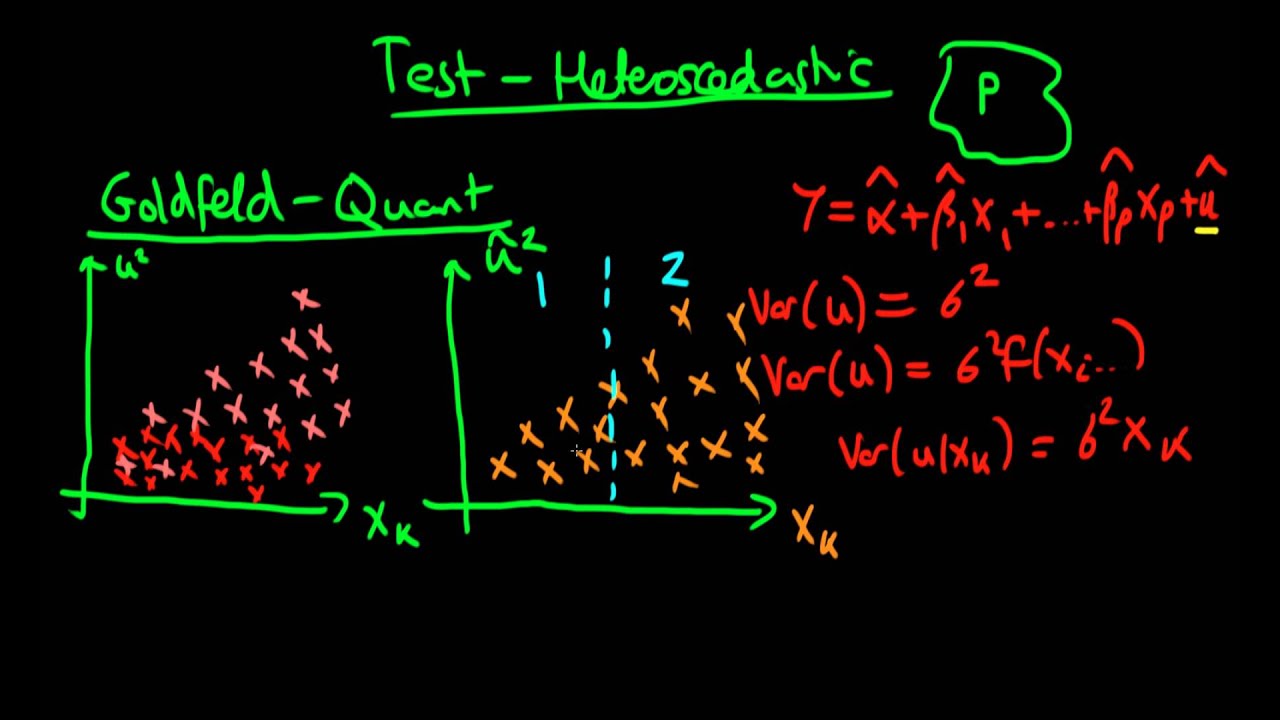
در تصویر زیر، فرض همواریانسی در باقیماندهها به ازاء مقادیر مختلف متغیر توصیفی (مستقل) دیده میشود.
برای مثال فرض کنید که مقادیر درآمد (Income) و هزینه (Consumption) برای چندین خانوار جمعآوری شده است و میخواهیم براساس یک مدل رگرسیونی، رابطه خطی بین درآمد و هزینه را مشخص کنیم. متغیر درآمد را به عنوان متغیر مستقل و هزینه را به عنوان متغیر وابسته در نظر گرفتهایم. اگر واریانس هزینهها به ازاء سطوح مختلف متغیر درآمد، دچار تغییر شود، مشکل ناهمواریانسی (Heteroscedasticity) در مدل رگرسیونی وجود خواهد داشت. تصویر زیر ناهمواریانسی را در جمله خطا به ازاء تغییرات متغیر مستقل نشان میدهد. مشخص است که با افزایش مقدار متغیر ، پراکندگی در بین مقادیر خطا بیشتر شده است.
فرض کنید مجموعه دادههای مدل رگرسیونی را به دو بخش تقسیم کردهایم. آزمون گلدفلد و کوانت در حقیقت برابری واریانس در بین این دو گروه را میسنجد. به این ترتیب مشخص میشود که آیا فرض همواریانسی در مدل رگرسیونی برقرار است یا مشکل ناهمواریانسی (Heteroscedasticity) در آن وجود دارد.
معمولا در این حالت ممکن است با استفاده از وزندهی به مشاهدات، مشکل ناهمواریانسی مرتفع میشود یا اضافه کردن متغیرهای توصیفی دیگر در مدل میتواند مشکل همواریانسی را حل کند. ولی اگر این موضوع مرتفع نشود، باید به دنبال روشهای رگرسیون غیر خطی رفته یا رگرسیونهای ناپارامتری مانند رگرسیون چندکی (Quantile Regression) را به کار بگیریم.
آزمون گلدفلد و کوانت (Goldfeld-Quandt Test) توسط دو اقتصاددان آمریکایی به نامهای «استفن گلدفلد» (Stephen Goldfeld) و «ریچارد کوانت» (Richard Quandt) طی مقالهای که در سال ۱۹۶۵ منتشر کردند، معرفی شود. آنها این آزمون را در دو نسخه پارامتری و ناپارامتری ارائه کردند ولی اغلب در تحقیقات و پژوهشها، منظور از آزمون گلدفلد و کوانت، نوع پارامتری آن است.
در این آزمون، فرض صفر وجود خاصیت همواریانسی (Homoscedasticity) است و فرض مقابل نیز عدم خاصیت همواریانسی را نشان میدهد که به ناهمواریانسی (Heteroscedasticity) نیز شهرت دارد.
آزمون پارامتری گلدفلد و کوانت
آزمون پارامتری گلدفلد و کوانت (Goldfeld-Quandt Parametric Test) با انجام تجزیه و تحلیل حداقل مربعات به صورت جداگانه روی دو زیر مجموعه از دادههای اصلی انجام میشود:
- گروه اول، شامل مشاهداتی است که مقدار متغیر مستقل برایشان کوچکتر از گروه دوم است.
- گروه دوم نیز شامل مشاهداتی است که مقدار همان متغیر مستقل، برایشان از گروه اول بیشتر است.
این زیرمجموعهها ممکن است دارای تعداد مشاهدات برابر نباشند و حتی اجتماع آنها نیز همه مشاهدات را پوشش ندهند. به این ترتیب میتوانیم با محاسبه واریانس متغیر وابسته یا جمله خطا برای این دو گروه، تغییرات واریانس را مورد بررسی قرار دهیم.
در آزمون پارامتری فرض میشود که خطاها دارای توزیع نرمال (Normal Distribution) است. البته یک فرض اضافی نیز در اینجا وجود دارد و آن این است که ماتریسهای طراحی (Design Matrix) برای دو زیر مجموعه از این دادهها دارای رتبه کامل (Full Rank) است. این امر به این معنی است که متغیرهای توصیفی از یکدیگر مستقل خطی هستند.
آماره آزمون گلدفلد و کوانت در حالت پارامتری، از نسبت میانگین مربعات باقیماندهها رگرسیونی در دو گروه ایجاد شده است. این آماره دارای توزیع فیشر (F Distribution) بوده و مطابقت با آزمون آماری فیشر (F-test) برای مساوی بودن واریانسها دارد. همچنین آزمون گلدفلد و کوانت، میتواند به صورت یک طرفه (one sided) یا دو طرفه (two sided) اجرا شود.
افزایش نقاط میانی (بین دو گروه) میتواند به توان آزمون کمک کند ولی در عوض باعث کاهش درجه آزادی آماره آزمون خواهد شد. معمولا با تغییر در تعداد مشاهدات میانی میتوان تغییر در کارایی آزمون گلدفلد و کوانت را مشاهده کرد. ناحیه میانی زمانی که بیش از یک متغیر توصیفی در مدل وجود داشته باشد، ایجاد میشود.
آزمون ناپارامتری گلدفلد و کوانت
آزمون دوم معرفی شده در مقاله گلدفلد و کوانت یک آزمون ناپارامتری (Non Parametric) است و از این رو به فرض نرمال بودن جمله خطا متکی نیست. برای انجام این آزمون، نیازی به تفکیک مجموعه دادهها نیست.
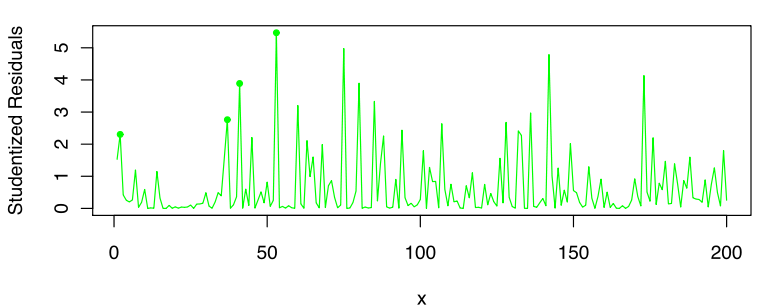
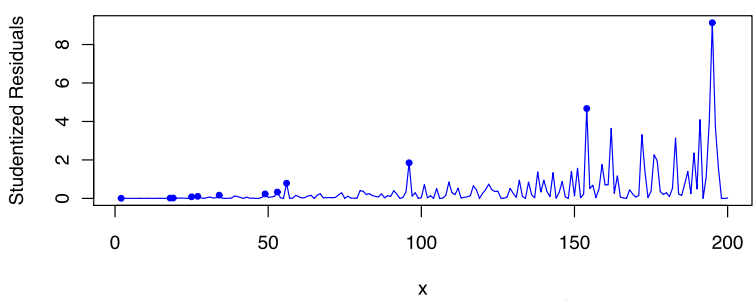
پس از آنکه مدل رگرسیون برازش شد، نمودار مربوط به مقادیر موثرترین متغیر مستقل و مربعات باقیماندهها ترسیم میشود، بطوری که محور افقی مقادیر مرتب شده متغیر مستقل است و محور عمودی مربوط به مقادیر باقیماندههای مدل رگرسیونی است.
آماره آزمون گلدفلد و کوانت ناپارامتری (Goldfeld-Quandt Parametric test) در این حالت، براساس تعداد قلههای موجود در این نمودار محاسبه میشود. یعنی، تعداد مواردی که مقدار باقیمانده از همه باقیماندههای قبلی در نمودار بزرگتر است. مقادیر بحرانی برای این آماره آزمون به کمک آزمونهای جایگشتی و روشهای بازنمونهگیری (Resampling) مانند جک نایف و بوت استرپ ساخته میشود.
مزایا و معایب آزمون گلدفلد و کوانت
آزمون پارامتری گلدفلد و کوانت (Goldfeld-Quandt) یک تشخیص ساده و شهودی را برای خطاهای حاصل از یک مدل رگرسیون چندگانه، ارائه میدهد. با این وجود برخی از معایب تحت شرایط خاص در مقایسه با سایر روشها (مانند آزمون Breush-Pagan) مشاهده میشود.
آزمون پارامتری گلدفلد و کوانت به عنوان یک روش خاص برای سنجش همواریانسی محسوب میشود و نمیتوان از آن به عنوان یک روش عمومی استفاده کرد. در درجه اول، در آزمون پارامتری گلدفلد و کوانت باید مشاهدات براساس یک متغیر توصیفی مشخص شده، مرتب شوند. بنابراین برای متغیرهای توصیفی که با مقیاس اسمی ثبت شدهاند کارایی ندارد.
اگر واریانس جمله خطا یا متغیر وابسته به یک متغیر توصیفی دیگر مرتبط باشد که در مدل لحاظ نشده، ممکن است آزمون گلدفلد و کوانت، فرض صفر را رد نکرده و رای به همواریانسی بدهند در حالیکه با ورود این متغیر جدید، احتمالا فرض صفر رد خواهد شد.
پیادهسازی آزمون گلدفلد و کوانت در زبان برنامهنویسی R
برای پیادهسازی آزمون گلدفلد و کوانت در زبانبرنامهنویسی R، از تابع gqtest از کتابخانه یا بسته lmtest استفاده میکنیم. شکل دستوری این تابع به صورت زیر است.
پارامترهای این تابع در ادامه معرفی شدهاند. البته توجه دارید که در هنگام استفاده از این تابع، به طور خودکار مشاهدات برحسب متغیرهای مستقل (توصیفی) مرتب میشوند.
- فرمول (Formula): همانطور که مشخص است بخش formula، به همان ترتیبی مشخص میشود که در تابع lm، مدل رگرسیونی و ارتباط بین متغیر وابسته و مستقل تعیین میشود. به این ترتیب ابتدا متغیر وابسته، سپس علامت ~ و بعد متغیرهای توصیفی (مستقل) قرار میگیرند. بین متغیرهای توصیفی ممکن است یکی از عملگرهای معرفی شده در جدول زیر نیز دیده شود.
| عنوان | علامت | شرح |
| Main Effect | a+b | اثرات اصلی یا رابطه خطی بین متغیر وابسته و مستقل a , b (جداسازی متغیرهای مستقل یا توصیفی در مدل) |
| Interaction | a:b | اثرات متقابل a و b بین متغیرهای مستقل روی متغیر وابسته |
| Main and Interaction Effect | * یا a+b+a:b | اثرات اصلی و متقابل بین متغیرهای مستقل a , b روی متغیر وابسته |
| Crossing | (a+b+c)^2 یا (a+b+c)*(a+b+c) | اثرات اصلی و متقابل درجه ۲ |
- پارامتر نقطه (Point): این پارامتر درصدی از مشاهدات را مشخص میکند که در حالت آزمون پارامتری برای تفکیک گروهها به کار میرود. اگر مقدار point بزرگتر از ۱ باشد، شماره مشاهدهای را نشان میدهد که باید عمل تفکیک مشاهدات به دو گروه از آن صورت گیرد. ولی اگر مقدار این پارامتر کمتر از ۱ و مثبت باشد، درصد تلقی شده و برای تعیین تعداد اعضای گروه اول به کار میرود.
- نسبت (Fraction): پارامتر fraction نیز میتواند به عنوان تعداد یا درصدی از دادهها که باید در میان مشاهدات نادیده گرفته شوند، تلقی شود.
- پارامتر نوع آزمون (Alternative): نوع آزمون یک طرفه یا دوطرفه توسط این پارامتر مشخص میشود.
به کمک کد زیر یک مجموعه از مقدارهای خطا ایجاد کردهایم که به دو گروه تفکیک شدهاند. در گروه اول از توزیع نرمال با میانگین ۵۰ و واریانس برای تولید مقادیر خطا استفاده شده و در گروه دوم از توزیع نرمال با میانگین صفر و واریانس ۱ (نرمال استاندارد) کمک گرفتهایم. به کمک آزمون گلدفلد و کوانت، میخواهیم برابری واریانس بین این دو گروه را بیازماییم.
کد زیر به این منظور تهیه شده است. به کتابخانههایی که توسط دستور install.packages و library نصب و راهاندازی شدهاند، توجه کنید.
خروجی به صورت زیر خواهد بود. همانطور که مشاهده میکنید، با توجه به مقدار احتمال (p-value=1.874e-07) که بسیار به صفر نزدیک است، فرض صفر که وجود همواریانسی در بین مقادیر خطا است، رد میشود. در نتیجه در متغیر err1 مشکل ناهمواریانسی (heteroskedastic) وجود دارد.
این بار، عبارت خطا را از توزیع نرمال با میانگین صفر و واریانس ۱ ایجاد میکنیم. میخواهیم بسنجیم که آیا مشکل ناهمواریانسی وجود دارد یا خیر.
پس از اجرای این کد، خروجی به صورت زیر دیده میشود. مشخص است که این بار مقدار احتمال (p-value=0.7477) از سطح آزمون (مثلا 0٫05) بزرگتر شده و فرض صفر رد نمیشود. پس باقیماندههای مدل همواریانس (Homoscedasticity) هستند.
خلاصه و جمعبندی
رگرسیون یک تکنیک آماری است که در یادگیری ماشین (Machine Learning) و دادهکاوی (Data Mining) به کار میرود. به همین علت کسانی که در حوزه علم داده (Data Science) مشغول به فعالیت هستند، لازم است که بر این گونه روشهای آماری مسلط شوند. در این نوشتار با نحوه بررسی خاصیت همواریانس برای مدل رگرسیون خطی با آزمون گلدفلد و کوانت (Goldfeld-Quandt Test) آشنا شده و همچنین نحوه پیادهسازی آن را در زبان برنامهنویسی R فرا گرفتیم. به این ترتیب یکی از فرضیات بسیار مهم در مدل رگرسیون خطی مورد پژوهش و ارزیابی قرار گرفت.
اگر مطلب بالا برای شما مفید بوده است، آموزشها و مطالبی که در ادامه آمدهاند نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار و احتمالات
- آموزش همبستگی و رگرسیون خطی در SPSS
- مجموعه آموزش برنامه نویسی R و نرم افزار RStudio
- رگرسیون کمترین زاویه (LAR Regression) — به زبان ساده
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- تحلیل واریانس (Anova) — مفاهیم و کاربردها
^^












