تعیین تنش برشی در تیرهای جدار نازک با مقطع باز — به زبان ساده

در مباحث قبلی، توزیع تنش‌های برشی در تیرهای مستطیلی، دایره‌ای و جان تیرها را مورد تحلیل قرار دادیم و رابطه برش برای تعیین تنش‌های موجود در تیرهای مذکور را مطابق زیر به دست آوردیم:

V: نیروی برشی اعمال شده بر سطح مقطع؛ I: ممان اینرسی سطح مقطع حول محور خنثی؛ b: عرض تیر در محل مورد تحلیل؛ Q: ممان اول سطح بیرونی محل تعیین تنش

در این مقاله قصد داریم تنش‌های برشی موجود در «تیرهای جدار نازک با مقطع باز» (Thin-walled Open-section Beams) را مورد بررسی قرار دهیم. تیرهای جدار نازک با مقطع باز دارای دو ویژگی متمایز هستند:

• الف) ضخامت جدار تیر نسبت به ارتفاع و عرض سطح مقطع آن کوچک است.
• ب) سطح مقطع تیر باز است (مانند تیرهای I شکل یا ناودانی).

فیلم آموزش مقاومت مصالح ۱ و ۲ – مرور و حل مساله در فرادرس

کلیک کنید

شکل زیر، چند نمونه از تیرهای جدار نازک با مقطع باز را نمایش می‌دهد. این نوع تیرها با عناوینی نظیر تیرهای دارای «مقطع سازه‌ای» (Structural Section) یا «مقطع نیمرخ» نیز گفته می‌شود.

فرآیند تحلیل

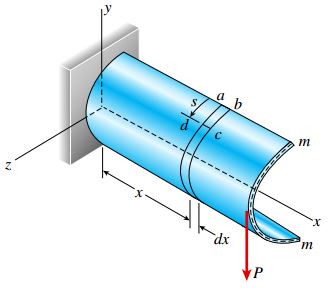
به منظور تعیین تنش‌های برشی موجود در تیرهای جدار نازک باز می‌توانیم از روشی مشابه با فرآیند تعیین رابطه برش استفاده کنیم. برای شروع، تیری را زیر در نظر بگیرید که محور سطح مقطع آن همانند شکل زیر دارای یک شکل نامنظم است. محورهای y و z، محورهای اصلی گذرنده از مرکز هندسی سطح مقطع (محورهای اصلی مرکزی) هستند.

فیلم آموزش مقاومت مصالح – ویژه رشته عمران در فرادرس

کلیک کنید

بار P نیز در جهت موازی با محور y اعمال می‌شود و از مرکز برش S عبور می‌کند. به این ترتیب، خمش در صفحه xy رخ می‌دهد و محور z به عنوان محور خنثی در نظر گرفته می‌شود.

تحت شرایط بالا، تنش نرمال اعمال شده بر هر نقطه دلخواه در تیر با استفاده از رابطه خمش به دست می‌آید:

M_z: گشتاور خمشی حول محور z و y: مختصات نقطه مورد نظر

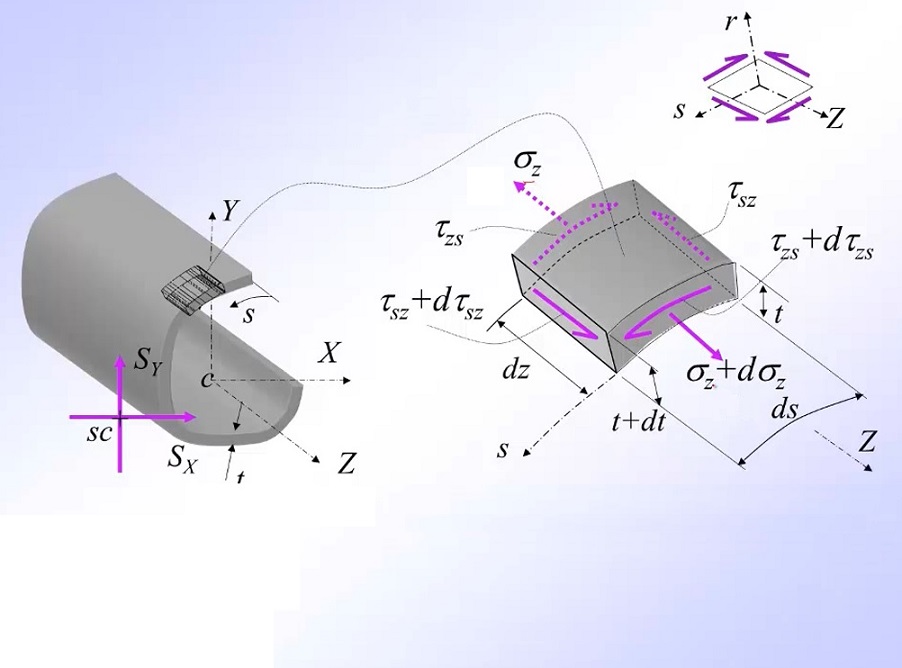
اکنون المان حجم abcd بین دو مقطع با فاصله dx از یکدیگر را در نظر بگیرید. توجه داشته باشید که این المان از لبه سطح مقطع شروع می‌شود. به علاوه، طول آن در امتداد محور mm برابر با s است.

به منظور تعیین تنش‌های برشی، المان abcd را به تنهایی در نظر بگیرید (شکل زیر). نیروی F₁، برآیند تنش‌های نرمال اعمال شده بر صفحه ad و نیروی F₂، برآیند تنش‌های نرمال اعمال شده بر صفحه bc است. به دلیل بزرگ‌تر بودن تنش‌های موجود بر روی bc (بزرگ‌تر بودن گشتاور خمشی)، نیروی F₁ بیشتر از F₂ خواهد بود. بنابراین، برای قرارگیری المان در حالت تعادل، تنش‌های برشی τ باید در راستای صفحه cd اعمال شوند. این تنش‌های برشی به صورت موازی با سطوح بالایی و پایینی المان و به همراه تنش‌های مکمل موجود بر روی سطوح ad و bc اعمال می‌شوند. برای ارزیابی تنش‌های برشی مذکور باید نیروهای موجود در راستای x المان را با هم جمع کنیم:

t: ضخامت سطح مقطع در سطح cd المان یا ضخامت سطح مقطع در فاصله s از لبه آزاد المان

در مرحله بعد، رابطه مورد نیاز برای تعیین نیروی F₁ را به دست می‌آوریم:

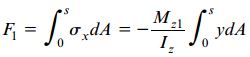
dA: یک المان سطح بر روی سطح ad المان؛ y: مختصات المان dA؛ و M_z1: گشتاور خمشی موجود در سطح مقطع

برای تعیین نیروی F₂ نیز از یک رابطه مشابه استفاده می‌کنیم:

با جایگذاری این روابط در τtdx=F₁-F₂، به معادله زیر می‌رسیم:

کمیت (M_z2-M_z1)/dx، نرخ تغییرات dM/dx (تغییرات گشتاور خمشی بر واحد طول) را نمایش می‌دهد و با نیروی برشی اعمال شده بر سطح مقطع برابر است:

نیروی برشی V_y با محور y موازی بوده و در جهت منفی این محور (جهت اعمال بار P) دارای علامت مثبت است. نحوه علامت‌گذاری در اینجا با قواعد علامت‌گذاری معرفی شده در مبحث «نیروی برشی و گشتاور خمشی در تیرها» مطابقت دارد. با جایگذاری رابطه بالا در رابطه قبلی، به معادله نیروی برشی τ می‌رسیم:

فیلم آموزش مقاومت مصالح – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

با کمک این معادله می‌توانیم تنش‌های برشی موجود در هر نقطه دلخواه بر روی سطح مقطع در فاصله s از لبه آزاد تیر را محاسبه کنیم. انتگرال موجود در این معادله، گشتاور اول سطح نسبت به محور z (محور خنثی) در فاصله s=0 تا s=s را نمایش می‌دهد. اگر این انتگرال را با Q_z نشان دهیم و معادله بالا را بازنویسی کنیم، فرم ساده‌تری از معادله تنش‌های برشی به دست می‌آید که معادلِ فرم استاندار رابطه برش است.

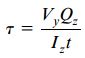
تنش‌های برشی بر روی محور سطح مقطع قرار می‌گیرند و موازی با لبه‌های آن عمل می‌کنند. شدت این تنش‌ها بر روی ضخامت جدار تیر ثابت در نظر گرفته می‌شوند. این فرض در صورت کوچک بودن ضخامت تیر کوچک معتبر خواهد بود. توجه داشته باشید که ضخامت جدار لزوماً ثابت نیست و امکان تغییر آن به صورت تابعی از فاصله s وجود دارد. جریان برش موجود در هر نقطه دلخواه بر روی سطح مقطع با حاصل‌ضرب تنش برشی در ضخامت در آن نقطه برابر است:

فیلم آموزش مقاومت مصالح ۲ در فرادرس

کلیک کنید

به دلیل ثابت بودن کمیت‌های V_y و I_z، جریان برش با Q_z رابطه مستقیم دارد. در بالا و پایین لبه‌های سطح مقطع، Q_z برابر صفر است. از این‌رو، جریان برش نیز در این نواحی برابر با صفر خواهد بود. مقدار جریان برش به طور پیوسته بین مقدار صفر (در نقاط انتهایی) و مقدار ماکسیمم (محل رخ دادن Q_z ماکسیمم در محور خنثی) تغییر می‌کند. اکنون فرض کنید که تیر نمایش داده شده در شکل زیر توسط بارهای موازی با محور z و گذرنده از مرکز برش تحت خمش قرار گرفته است. بنابراین، تیر در صفحه xz خم شده و محور y به عنوان محور خنثی در نظر گرفته می‌شود.

در این حالت، با تکرار مراحل توضیح داده شده در حالت قبلی به معادلات تنش‌های برشی و جریان برش می‌رسیم:

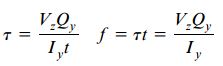
V_z: نیروی برشی موازی با محور z؛ و Q_y: گشتاور اول سطح نسبت به محور y

در این مقاله، روابط مورد نیاز برای تعیین تنش‌های برشی موجود در تیرهای جدار نازک باز با شرط گذر نیروی برشی از مرکز برش و موازی بودن آن با یکی از محورهای اصلی به دست آمدند. اگر بین نیروی برشی و محورهای y و z زاویه‌ای وجود داشته باشد؛ در صورت عبور نیروی برشی از مرکز برش می‌توان آن را به مؤلفه‌های موازی با محورهای اصلی تجزیه کرد، هر یک از این مؤلفه‌ها را جداگانه مورد تحلیل قرار داد و در نهایت، برآیند تنش‌های برشی مورد نظر را با استفاده از برهم‌نهی مؤلفه‌های تنش به دست آورد. دو مورد از کاربردهای معادلات معرفی شده در این مقاله، تعیین تنش‌های برشی موجود در تیرهای بال پهن و تعیین محل قرارگیری مرکز برش تیرهای جدار نازک است. در مباحث بعدی، به تشریح این مباحث خواهیم پرداخت.

^^