هم خطی در مدل رگرسیونی – به زبان ساده

در رگرسیون خطی بخصوص در روش OLS، شرط مستقل بودن «متغیرهای توصیفی» (Explanatory Variable) از اهمیت خاصی برخوردار است. به این علت قبل از انجام رگرسیون خطی باید از عدم همخطی در مدل اطمینان داشته باشیم تا نتایج حاصل از مدل رگرسیونی معتبر باشند. در حقیقت هم خطی در مدل رگرسیونی به وجود همبستگی بین متغیرهای مستقل اشاره دارد. در این نوشتار با مشکل «همخطی» (Collinearity) و «همخطی چندگانه» (Multicollinearity) آشنا شده و نحوه غلبه بر آن‌ها در مدل رگرسیونی را فرا می‌گیریم.

همخطی و همخطی چندگانه، در تکنیک «رگرسیون چندگانه معمولی» (OLS)، نتایج را غیر معتبر می‌کند. ولی اگر از روش‌های دیگر رگرسیونی استفاده شود، مشکل همخطی، اعتبار مدل را از بین نخواهد برد. اما از آنجایی که رگرسیون OLS محبوبیت و کاربرد زیادی دارد، درک مشکل همخطی و رفع آن ضروری به نظر می‌رسد.

برای آشنایی با شیوه محاسبات در رگرسیون خطی چندگانه، مطلب رگرسیون خطی چندگانه (Multiple Linear Regression) --- به زبان ساده را بخوانید. از طرفی خواندن نوشتار رگرسیون خطی — مفهوم و محاسبات به زبان ساده نیز از شرط‌های اعتبار رگرسیون خطی شما را مطلع می‌سازد. همچنین مطالعه تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست.

هم خطی در مدل رگرسیونی

«همخطی» (Collinearity) پدیده‌ای است که به بیان وضعیتی می‌پردازد که یک «متغیر توصیفی» (Explanatory Variable) در «رگرسیون چندگانه» (Multiple Regression) با یک یا چند متغیر دیگر دارای رابطه خطی است به طوری که می‌توان آن را به صورت ترکیب خطی از دیگر متغیرها در نظر گرفت. به این ترتیب «همخطی چندگانه» (Multicollinearity) نیز وضعیتی را نشان می‌دهد که بین چندین متغیر توصیفی رابطه خطی وجود داشته باشد و بتوان آن‌ها را به صورت ترکیب خطی از یکدیگر نوشت.

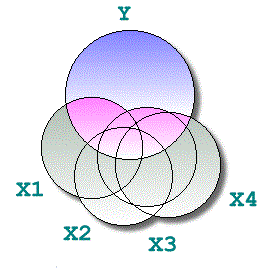
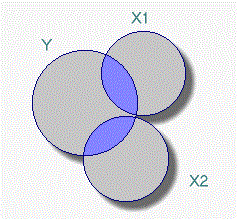
در اصل با توجه به روش رگرسیون چندگانه و فرضیات آن، وجود استقلال در بین متغیرهای توصیفی ضروری است. اگر به تصویر زیر توجه کنید، مشخص است که سهم متغیرهای $$X_1, X_2, X_3,X_4$$ در بیان تغییرات متغیر $$Y$$ به صورتی است که هیچ وجه اشتراکی بین متغیرهای توصیفی وجود ندارد. به بیان دیگر متغیرهای توصیفی مستقل از یکدیگر هستند. در نمودارهایی که در ادامه می‌بینید، ناحیه آبی رنگ مربوط به میزان سهمی است که هر متغیر برای بیان یا پیش‌بینی متغیر پاسخ دارد. همچنین رنگ صورتی در این نمودارها برای نشان دادن اشتراکی است که بین دو متغیر مستقل وجود دارد.

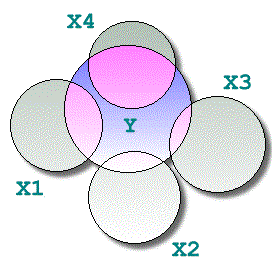
زمانی که همخطی یا همخطی چندگانه در یک مدل رگرسیون چند گانه وجود داشته باشد، ضرایب مدل حاصل معتبر نیستند، زیرا اثر هر یک از متغیرها توصیفی روی «متغیر پاسخ» (Response Variable) شامل اثر متغیرهای دیگر در مدل نیز هست. بنابراین واریانس برآوردگرهای ضرایب رگرسیونی افزایش یافته و در عمل پیش‌گویی توسط مدل رگرسیونی با خطای زیادی همراه خواهد بود. به این ترتیب با تغییری اندک روی داده‌های به کار رفته در مدل، ضرایب رگرسیونی به شدت تغییر خواهند کرد. تصویر زیر به بررسی وضعیت همخطی چندگانه در بین متغیرهای توصیفی $$X_1, X_2, X_3,X_4$$ در بیان تغییرات متغیر $$Y$$ در مدل رگرسیونی می‌پردازد. همانطور که دیده می‌شود اثر یک متغیر ممکن است بیش از یک بار روی متغیر پاسخ سنجیده شود.

نکته: از آنجایی که همخطی، حالت خاصی از همخطی چندگانه محسوب می‌شود، از این به بعد منظورمان هنگام استفاده از عبارت همخطی هر دو حالت همخطی و همخطی چندگانه است.

با توجه به میزان همخطی یا همخطی چندگانه بین متغیرهای مستقل یا توصیفی، مسئله همخطی را به دو نوع تقسیم می‌کنند: «همخطی کامل» (Perfect Multicollinearity) و «همخطی ناقص» (Nearly Multicollinearity). در ادامه به بررسی انواع هم‌خطی خواهیم پرداخت.

هم‌خطی کامل (Perfect Multicollinearity)

در همخطی کامل، دو یا چند متغیر توصیفی (مستقل) با یکدیگر رابطه کامل خطی دارند. به این ترتیب می‌توان بعضی از متغیرهای توصیفی را به صورت رابطه خطی از یک یا چند متغیر دیگر بیان کرد. به بیان ریاضی اگر بین $$k$$ متغیر $$X_1, X_2, \cdots, X_k$$ همخطی کامل برقرار باشد می‌توانیم رابطه زیر را برای مشاهده iام بنویسیم.

$$\large \lambda _{0}+\lambda _{1}X_{{1i}}+\lambda _{2}X_{{2i}}+\cdots +\lambda _{k}X_{{ki}}=0$$

رابطه ۱

در این رابطه مقدارهای $$\lambda$$ برای همه مشاهدات ثابت است. حال فرض کنید مدل رگرسیونی با وجود $$k$$ متغیر مستقل به صورت زیر نوشته شده است.

$$\large Y_{{i}}=\beta _{0}+\beta _{1}X_{{1i}}+\cdots +\beta _{k}X_{{ki}}+\varepsilon _{{i}}$$

همانطور که در نوشتار رگرسیون چندگانه مطرح شد، در تکنیک OLS از معکوس ماتریس $$X^TX$$ استفاده می‌شود. باید توجه داشت که ماتریس $$X$$ در روش OLS به صورت زیر نوشته می‌شود.

$${\displaystyle X={\begin{bmatrix}1&X_{11}&\cdots &X_{k1}\\\vdots &\vdots &&\vdots \\1&X_{1N}&\cdots &X_{kN}\end{bmatrix}}}$$

مشخص است که این ماتریس دارای $$N$$ سطر و $$(k+1)$$ ستون است. در صورتی که بین سطرها یا ستون‌های این ماتریس رابطه خطی مطابق با رابطه ۱ وجود داشته باشد، ماتریس $$X^TX$$ معکوس‌پذیر نبوده و امکان استفاده از روش OLS وجود ندارد. زیرا دترمینان این ماتریس صفر بوده و ماتریس پر رتبه نخواهد بود.

هم‌خطی ناقص (Nearly Multicollinearity)

اگر رابطه بین متغیرهای مستقل به صورت نزدیک به رابطه خط باشد، همخطی ناقص رخ داده است.

فیلم آموزش کاربرد رگرسیون و همبستگی در آمار استنباطی برای مدیریت و علوم انسانی (رایگان) در فرادرس

کلیک کنید

در این صورت می‌توان فرض کرد که رابطه بین متغیرهای توصیفی یا مستقل به صورت زیر است.

$$\large \lambda _{0}+\lambda _{1}X_{{1i}}+\lambda _{2}X_{{2i}}+\cdots +\lambda _{k}X_{{ki}}+v_{i}=0$$

رابطه ۲

در چنین وضعیتی، وجود عبارت $$v_i$$ باعث می‌شود که رابطه دقیق خطی از بین رفته و این رابطه از یک مشاهده به مشاهده دیگر متفاوت باشد. اگر واریانس $$v$$ کوچک باشد، باز هم مدل رگرسیونی دچار همخطی تقریبا کامل خواهد شد ولی ممکن است ماتریس $$X^TX$$ معکوس پذیر باشد. اگر پارامترهای مدل رگرسیونی را با توجه به همخطی ناقص، برآورد کنیم، خواهیم دید که با تغییر کوچک روی مقدار مشاهدات، برآوردها به شدت تغییر خواهند کرد و این نشانه از حساسیت زیاد مدل به تغییرات کوچک داده‌های نمونه است. واضح است که این امر باعث نامعتبر شدن مدل خواهد شد. در ادامه به بررسی وضعیت‌های مختلفی که در مورد همخطی ممکن است رخ دهد می‌پردازیم.

رابطه سلسله مراتبی در هم‌خطی

فرض کنید دو متغیر توصیفی $$X_1$$ و $$X_2$$ در یک مدل رگرسیونی به منظور پیش‌بینی متغیر پاسخ $$Y$$ حضور دارند. اگر تاثیر یکی از متغیرهای توصیفی روی متغیر پاسخ به واسطه متغیر توصیفی دیگر صورت بگیرد، همخطی سلسله مراتبی بوجود آمده است. با توجه به تصویر زیر به نظر می‌رسد که متغیر $$X_2$$ روی متغیر $$Y$$‌ تاثیر گذار نیست ولی اثر آن بواسطه همبستگی که بین متغیر $$X_1$$ و $$X_2$$ وجود دارد، اعمال می‌شود. بنابراین استفاده از متغیر $$X_1$$ در مدل به تنهایی می‌تواند مناسب باشد.

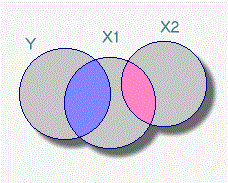
رابطه هم‌خطی ناقص

در این حالت بین دو متغیر $$X_1$$ و $$X_2$$ همبستگی وجود دارد ولی تقریبا سهم هر یک این متغیرها در بیان تغییرات متغیر پاسخ یکسان است. در چنین حالتی تغییرات یکی از متغیرهای مستقل می‌تواند در ضریب متغیر مستقل دیگر در مدل رگرسیونی تاثیر گذار باشد.

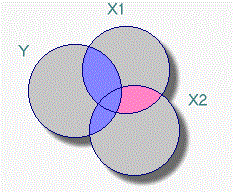
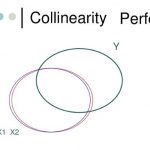
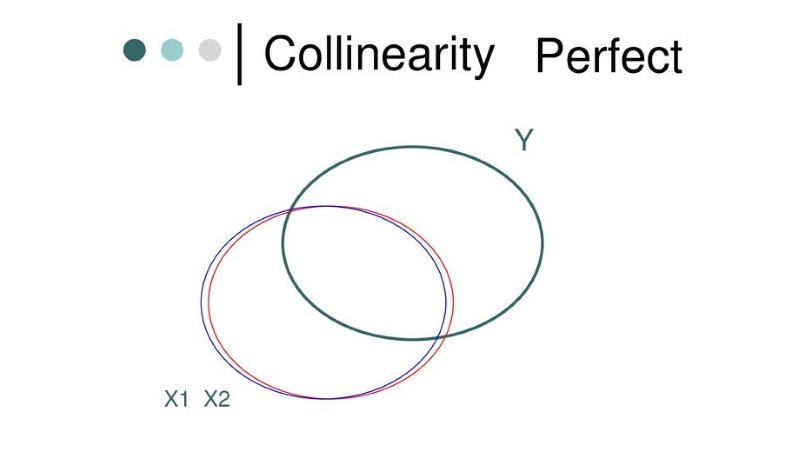
رابطه هم‌خطی کامل

با توجه به نمودار زیر مشخص است که متغیرهای توصیفی $$X_1$$ و $$X_2$$ بسیار به یکدیگر نزدیکند به طوری که در بیشتر مواقع دارای مقدار مشترک هستند. به این ترتیب اثر هر یک از متغیرها روی متغیر پاسخ، بوسیله متغیر دیگر نیز قابل بیان است. پس بوسیله هر یک از این متغیرها به تنهایی، می‌توان متغیر پاسخ را پیش‌بینی کرد. در چنین حالتی همخطی کامل بین متغیرهای مستقل، باعث افزایش واریانس در پارامترهای مدل رگرسیونی خواهد شد.

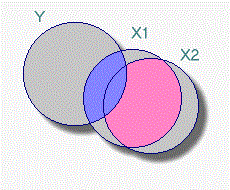
بدون رابطه هم‌خطی

اگر بین متغیرهای مستقل، هیچ رابطه‌ای وجود نداشته باشد، میزان سهمی که هر یک از پیشگویی متغیر پاسخ دارند به نسبت اهمیت یا بزرگی ضرایب استاندارد شده آن‌ها در مدل است. بنابراین با توجه به نموداری که در ادامه قابل مشاهده است، باید هر دو متغیر $$X_1$$ و $$X_2$$ در مدل به منظور پیشگویی متغیر $$Y$$ حضور داشته باشند زیرا سهم هر یک در تغییر پذیری متغیر پاسخ نسبتا زیاد است. در چنین حالتی مشکل همخطی وجود ندارد.

روش‌های شناسایی هم‌خطی

به منظور شناسایی هم‌خطی بهتر است از روش‌های زیر بهره ببرید. البته در بیشتر موارد هر یک از این تکنیک‌ها، تایید کننده روش‌های دیگر هستند. ولی بهتر است برای شناسایی وجود همخطی بین متغیرها حداقل از دو روش برای بررسی استفاده کرد.

1. تغییرات بزرگ در برآورد ضرایب رگرسیونی، زمانی که یک متغیر توصیفی اضافه یا حذف می‌شود.
2. آزمون فرض در مورد هر یک از ضرایب رگرسیون در رگرسیون چندگانه رای به بی‌معنا بودن آن‌ها داده در حالیکه جدول تحلیل واریانس مدل رگرسیونی را مناسب تشخیص می‌دهد. به بیان دیگر فرض صفر بودن ضرایب در آزمون F رد می‌شود.
3. وجود تناقض بین نتایج حاصل از رگرسیون ساده تک متغیری و رگرسیون چندگانه به طوری که در آزمون مربوط به رگرسیون چندگانه، فرض صفر بودن ضریب یک متغیر توصیفی تایید شده در حالیکه در رگرسیون ساده یک متغیری، آزمون صورت گرفته نشانگر معنی‌دار بودن ضریب مربوط به آن متغیر باشد.
4. استفاده از معیارهای «میزان تحمل» (Tolerance) و یا «عامل تورم واریانس» (Variance Inflation Factor) که به اختصار VIF نامیده می‌شود، برای مدل رگرسیونی. در این حالت رابطه محاسباتی برای این دو شاخص به صورت زیر نوشته می‌شود.

$$\large {\mathrm {Tolerance}}=1-R_{{j}}^{2},\quad {\mathrm {VIF}}={\frac {1}{{\mathrm {tolerance}}}}$$

در این رابطه منظور از $$R^2_j$$ ضریب «تعیین مدل» (R Square) مدل رگرسیونی روی متغیر توصیفی $$j$$ام به عنوان متغیر پاسخ با متغیرهای توصیفی دیگر به عنوان متغیرهای مستقل است. در صورتی که میزان Tolerance کمتر از 0.1 و یا VIF بیشتر از 10 باشد، رای به وجود همخطی بین متغیرهای مستقل می‌دهیم.

رفع مشکل هم‌خطی

یکی از مشکلاتی که همخطی در مدل رگرسیونی به روش OLS ایجاد می‌کند، بیش‌برازش (Overfitting) است. به این معنی که برای ایجاد مدل رگرسیونی، از متغیرهای زیادی استفاده شده تا میزان خطا کاهش یابد ولی به محض تغییر یکی از داده‌ها و اجرای برازش مجدد، پارامترها به شدت تغییر کرده و مدل کاملا متفاوتی نسبت به قبل ایجاد می‌شود. برای رفع چنین حالت می‌توان از راهکارهای مختلفی که در فهرست زیر معرفی شده‌اند کمک گرفت.

1. استفاده از روش «رگرسیون گام به گام» (Stepwise Regression) به منظور ورود متغیرهایی که بیشترین میزان ارتباط با متغیر وابسته را دارند.
2. استفاده از «رگرسیون ستیغی» (Ridge Regression) برای کاهش تعداد متغیرها و دخیل کردن متغیرهایی که بیشترین وابستگی را دارند. این کار بوسیله ایجاد پارامتر جریمه نسبت به تعداد متغیرهای مستقل در هنگام برآورد پارامترهای مدل رگرسیون صورت می‌گیرد.
3. استفاده از روش‌های دیگری برآورد پارامترهای رگرسیونی مانند رگرسیون لاسو (Lasso Regression)، تا بتوان از بیش‌برازش مدل جلوگیری کرد.
4. استفاده از مشاهدات بیشتر در روش OLS به منظور کاهش خطای مدل و واریانس برآوردگرها.
5. استاندارد کردن داده‌ها قبل از اجرای برآورد پارامترهای مدل رگرسیونی.
6. استفاده از تکنیک تحلیل مولفه‌های اصلی PCA یا (Principle Components Analysis) به منظور کاهش بعد مسئله و استفاده از مولفه‌های اصلی در ایجاد مدل رگرسیونی. از آنجایی که این مولفه‌ها دارای کمترین همبستگی هستند، مشکل همخطی در مدل توسط این مولفه‌ها رفع خواهد شد.
7. استفاده از روش رگرسیون لار (Lar Regression) زمانی که تعداد متغیرها نسبت به مشاهدات زیاد بوده و ماتریس $$X^TX$$ معکوس پذیر نباشد.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های SPSS
• مجموعه آموزش‌های نرم‌افزارهای آماری
• آموزش همبستگی و رگرسیون خطی در SPSS
• آموزش آنالیز واریانس با SPSS
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• تحلیل واریانس (Anova) — مفاهیم و کاربردها

^^