معکوس ماتریس یا ماتریس وارون – به زبان ساده (+ دانلود فیلم آموزش گام به گام)
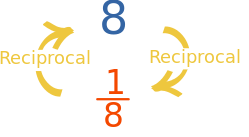
در این مطلب از مجله فرادرس در مورد معکوس ماتریس یا وارون ماتریس که در کتاب هندسه تحلیلی توضیح داده شده است، صحبت میکنیم. میدانیم که ماتریس آرایهای مستطیلی از اعداد است که در یک یا چند سطر و ستون مرتب شدهاند. در برخی عملیاتهایی که بر روی ماتریس صورت میگیرد، مثلاً در زمان تقسیم دو ماتریس لازم میشود که ما معکوس ماتریس را نیز محاسبه کنیم. اما منظور از معکوس ماتریس چیست؟ برای این که معکوس ماتریس را بهتر توضیح دهیم، ابتدا معکوس یک عدد را بررسی میکنیم. معکوس هر عددی حاصل تقسیم 1 بر آن عدد است. برای مثال معکوس عدد 8 برابر با 1/8 است:
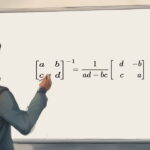
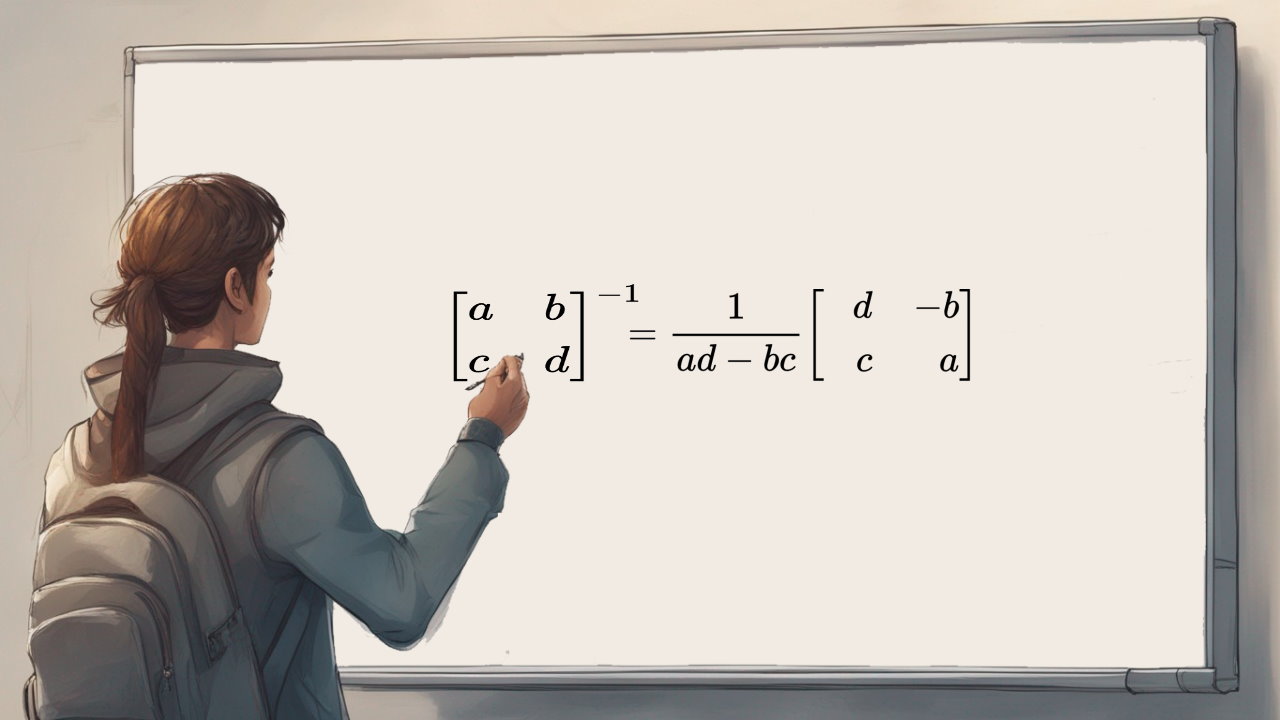
فیلم آموزشی معکوس ماتریس یا ماتریس وارون
معکوس (Inverse) یک ماتریس نیز به همین طریق محاسبه میشود، اما آن را با A-1 نشان میدهیم. توجه داشته باشید که مفاهیم ترانهاده ماتریس و معکوس ماتریس با یکدیگر متفاوت هستند.

شاید بپرسید چرا معکوس ماتریس را به صورت(A/1) نمینویسیم؟ چون ما ماتریس را نمیتوانیم تقسیم کنیم. دلیل دیگر آن است که 1/8 را نیز میشود به شکل 1-8 نوشت. البته شباهتهای دیگری نیز وجود دارند:
- وقتی یک عدد را در معکوسش ضرب می کنید، عدد 1 بدست می آید.
8 × (1/8) = 1
- هنگامی که یک ماتریس را در معکوس آن ضرب می کنیم، ماتریس همانی به دست میآید که معادل همان عدد 1 برای ماتریسها است:
A × A-1 = I
- گفتههای بالا در صورتی که معکوس در ابتدای ضرب باشد نیز صدق میکند:
(1/8) × 8 = 1
A-1 × A = I
ماتریس همانی
در بالا به «ماتریس همانی» یا «ماتریس یکّه» (Identity Matrix) اشاره کردیم. این ماتریس برابر با عدد 1 است.
در تصویر زیر مثالی از یک ماتریس همانی 3×3 ارائه شده است:

- این ماتریس، «مربعی» است (تعداد سطر و ستون برابر دارد)،
- درایه های روی قطر اصلی 1 و بقیه درایه ها برابر 0 است.
- علامت آن حرف بزرگ انگلیسی I است.
ماتریس همانی می تواند به اندازه 2×2، 3×3، 4×4 و ... باشد.
تعریف معکوس ماتریس
معکوس ماتریس A برابر A-1 است، تنها اگر:
A × A-1 = A-1 × A = I
البته بعضی ماتریسها هم وجود دارند که هیچ معکوسی ندارند. تعریف بالا برای تمامی ماتریسهای ۲×۲ یا ۳×۳ و ماتریسهای مرتبه بالاتر نیز صادق است.
ماتریس 2×2
اینک سعی میکنیم معکوس یک ماتریس 2×2 را محاسبه کنیم؟
معکوس ماتریس 2×2 این گونه محاسبه میشود:
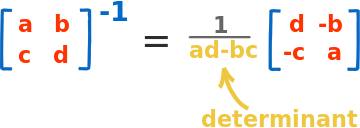
به عبارت دیگر برای محاسبه معکوس این ماتریس باید مکان درایههای a و d را عوض کنید، در مقابل درایه های b و c علامت منفی قرار دهید، و تمامی درایه ها را بر دترمینان ماتریس اولیه تقسیم کنید (ad – bc).
با یک مثال عددی این مسئله را بیشتر توضیح میدهیم:
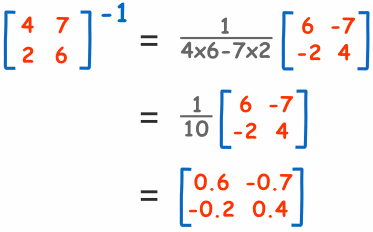
از کجا میدانیم که این پاسخ درست است؟
اگه به خاطر سپرده باشید، پیشتر اشاره کردیم که با ضرب یک ماتریس در معکوسش، یک ماتریس همانی به دست میآید، یعنی A × A-1 = I. اینک میتوانیم با این آزمون بررسی کنیم که آیا معکوس ماتریس را به درستی محاسبه کردهایم یا نه.

میبینیم که حاصلضرب برابر با ماتریس همانی است. پس پاسخ قطعاً درست است. همچنین رابطه A-1 × A = I نیز باید در میان یک ماتریس و معکوسش برقرار باشد. شما به عنوان یک آزمون میتوانید ضرب را انجام دهید تا ببینید که آیا نتیجه برابر ماتریس همانی است یا نه.

کاربرد معکوس یک ماتریس چیست؟
ماتریس ها تقسیم نمیشوند و در واقع، هیچ مفهومی به عنوان تقسیم یک ماتریس وجود ندارد. اما میتوانیم یک ماتریس آن را در معکوسش ضرب کنیم. این کار همان چیزی را که می خواهیم به ما میدهد. فرض کنید اعداد را نمیتوانستیم تقسیم کنیم و یک نفر میپرسید «چگونه 10 سیب را بین دو نفر تقسیم کنم؟».
با توجه به این که همیشه میتوانیم معکوس عدد 2 که برابر 0.5 است، را به دست آورد، پس در این صورت میشد پاسخ داد:
10 × 0.5 = 5
هر کدام از آنها 5 سیب می گیرند. همین کار را میشود برای ماتریسها نیز انجام داد. فرض کنید ماتریس های A و B معلوم هستند و میخواهید ماتریس مجهول X را طوری به دست آورید که:
XA = B
بسیار خوب میشد که طرفین را بر A تقسیم کنیم تا عبارت X = B/A بدست آید؛ اما در نظر داشته باشید که ماتریسها را نمیشود تقسیم کرد. بنابراین چگونه سوالی که پیش میآید این است که آیا میتوان طرفین رابطه فوق را در معکوس ماتریس (یعنی A-1) ضرب کرد؟
XAA-1 = BA-1
می دانیم که A × A-1 = I، پس:
XI = BA-1
می توانیم I را حذف کنیم (همانگونه که عدد 1 را می شود در معادله 1x = ab حذف نمود):
X = BA-1
و با در نظر گرفتن این که می توانیم A-1 را محاسبه کنیم، پاسخ را به دست میآوریم.
در مثال ذکر شده، مراقب بودیم که ضربها را با ترتیب صحیحی انجام دهیم، چرا که در ضرب ماتریسها، تغییر ترتیب ماتریسها پاسخ را تغییر میدهد و خاصیت جابهجایی در مورد آنها صدق نمیکند. AB تقریباً هیچ گاه با BA برابر نیست.
یک مثال کاربردی: اتوبوس و قطار
گروهی از افراد به یک مسافرت با اتوبوس رفتند. که هر کودک 3 دلار و از هر بزرگسال 3.20 دلار به عوان هزینه بلیت دریافت شد. مجموع هزینههای بلیتها برابر با 118.40 دلار شد. در مسیر برگشت، به جای اتوبوس از قطار استفاده شد و از هر کودک 3.50 دلار و از هر بزرگسال 3.60 دلار اخذ گردید و این بار مجموع هزینه بیلیتها 135.20 دلار شد. اینک باید محاسبه کنید، چه تعداد کودک و چه تعداد بزرگسال داریم؟
برای محاسبه پاسخ ابتدا اجازه دهید که ماتریس ها را تشکیل دهیم. اما باید مراقب باشید که سطرها و ستونها را درست جایگذاری کرده باشید.

این ماتریسها دقیقاً بیانگر مثال بالا هستند:
XA = B
بنابراین برای حل مسئله، باید معکوس A را به دست آوریم:

اکنون که معکوس را داریم، مسئله را میتوانیم با معادله زیر حل کنیم:
X = BA-1

در این مسئله، 16 کودک و 22 بزرگسال داشتیم. پاسخ تقریباً شبیه یک جادو ظاهر می شود، اما در واقع این پاسخ بر اساس محاسبات صحیح ریاضی به دست آمده است.
محاسباتی مانند این و البته با استفاده از ماتریسهای بسیار بزرگتر، به مهندسان کمک میکند که بتوانند ساختمانها را طراحی کنند. از این محاسبات همچنین در بازیهای ویدئویی و انیمیشنهای رایانهای استفاده میشود تا جلوههای سهبعدی به آنها ببخشند. از این روش برای امور بسیار دیگری نیز استفاده میشود. این روش همچنین برای حل دستگاه معادلات خطی استفاده میشود. محاسبات توسط کامپیوتر انجام میشود؛ اما افراد عادی نیز نیاز دارند که فرمولها را درک کرده و متوجه شوند.
ترتیب ماتریسها مهم است
فرض کنید در معادله زیر میخواهیم X را بیابیم:
AX = B
این معادله با مثال بالا فرق دارد، چون اینجا X اکنون بعد از A قرار دارد. در ضرب ماتریس ها، تغییر ترتیب معمولاً پاسخ را عوض می کند بنابراین باید توجه داشته باشید که AB ≠ BA. باید به این نکته مهم توجه داشته باشید و بدانید که تغییر ترتیب ماتریسها در ضرب همیشه نتیجه را عوض میکند.
خب پس چگونه معادله زیر را حل می کنیم؟ می توانیم با همان روش معادله زیر را نیز حل کنیم، اما باید A-1 را قبل از A قرار دهیم:
A-1AX = A-1B
میدانیم که A-1A = I است، پس:
IX = A-1B
میتوانیم I را نیز حذف کنیم:
X = A-1B
و با در نظر گرفتن این که می توانیم A-1 را محاسبه کنیم، میبینیم که پاسخ را به دست آوردهایم.
حل مثال قطار و اتوبوس به روش معکوس ماتریس
سوالی که اینجا مطرح میشود این است که آیا میتوانیم مثال اتوبوس و قطار را نیز به این روش حل کنیم؟ پاسخ مثبت است، آن مثال را نیز میتوان این گونه حل کرد. فقط باید مراقب باشید که چگونه ماتریسها را تشکیل میدهید.
این ماتریس به شکل معادله AX = B است:

این روش به نظر بسیار مرتب و منظم میآید و شاید این روش را بیشتر ترجیح بدهید. باید در نظر داشته باشید که چگونه جای سطرها و ستونها را در مقایسه با مثال قبلی عوض میکنیم. برای حل این مثال به معکوس A نیاز داریم:
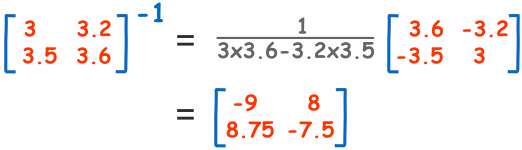
مانند روش معکوسی است که دقعات پیش عمل کردیم ؛ اما این بار ترانهاده محاسبه میشود، یعنی جای سطرها و ستونها عوض می شوند. اکنون میتوانیم با معادله زیر آن را حل کنیم:
X = A-1B

میبینیم که همان پاسخ به دست میآید: 16 کودک و 22 بزرگسال. پس دانستیم که ماتریسها برای حل مسائل بسیار قدرتمند، مناسب هستند؛ اما باید دقت کنیم که ماتریسها همواره به شکل صحیحی تشکیل شوند، یعنی دادهها در درایههای مناسب خود قرار گیرند.
ممکن است معکوس ماتریس وجود نداشته باشد
اول از همه، برای این که ماتریسی معکوس داشته باشد، آن ماتریس باید «مربعی» باشد، یعنی تعداد سطرها و ستونهای آن با هم برابر باشند. از طرف دیگر دترمینان این ماتریس باید غیر صفر باشد. چون در غیر این صورت به وضعیت تقسیم بر صفر میرسیم که غیر ممکن است.
به مثال زیر توجه کنید:

میبینیم که در نهایت، در مخرج کسر عبارت 24-24 را به دست آوردهایم که حاصل آن برابر 0 می شود و چون 1/0 تعریف نشده است، نمی توانیم بیش از این جلوتر برویم. نتیجه این که این ماتریس، معکوس ندارد. ماتریسی مانند این را ماتریس «منفرد» (Singular) می نامند، که دارای دترمینان صفر است. با اندکی توجه میبینیم که در این ماتریس، سطر دوم دو برابر سطر اول است و در واقع اطلاعات جدیدی را در اختیار نمیگذارد. فرض کنید اگر در مثال بالا قیمتهای قطار دقیقا 50% بیشتر بود، دیگر اطلاعات این ماتریس، ما را به یافتن تعداد کودکان و بزرگسالان نزدیک نمیکرد، چون ما نیازمند اطلاعات بیشتری بودیم. محاسبه دترمینان صفر نیز گفته ما را تایید می کند.
ماتریسهای بزرگتر
یافتن معکوس یک ماتریس 2×2 در مقایسه با ماتریسهای بزرگتر، از جمله ماتریس های 3×3، 4×4 و غیره، کار آسانی است. برای ماتریسهای بزرگتر، 3 روش اصلی برای یافتن معکوس ماتریس وجود دارد:
- یافتن معکوس یک ماتریس با استفاده از عملیات مقدماتی سطرها یعنی روش «گاوس – جردن» (Gauss – Jordan)
- یافتن معکوس یک ماتریس با استفاده از «کهاد» (Minor)، «همساز» (Cofactor) و «ماتریس همساز» (Adjugate)
- یافتن معکوس ماتریس با استفاده از رایانه و نرمافزارهای مختلفی که به این منظور طراحی شده اند.
جمعبندی
- معکوس ماتریس A برابر است با A-1 ، اگر و فقط اگر A × A-1 = A-1 × A = I
- برای یافتن معکوس یک ماتریس 2×2، ابتدا جای درایه های a و d را عوض کنید، در مقابل b و c علامت منفی بگذارید، و سپس کل اعضا را بر دترمینان تقسیم کنید (ad – bc).
- در بعضی موارد ماتریس، کلاً معکوسی ندارد.
آزمون ماتریس وارون
۱. کدام گزینه ویژگی اساسی ماتریس همانی (Identity Matrix) را بیان میکند؟
همه ردیفها و ستونها فقط شامل عدد صفر هستند.
تمام درایههای روی قطر اصلی برابر ۱ و سایر درایهها صفر هستند.
قطر اصلی شامل اعداد ترتیبی مثل ۱، ۲، ۳ است.
درایههای بالا و پایین قطر اصلی مقادیر برابر دارند.
ماتریس همانی به این دلیل متمایز است که فقط درایههای روی قطر اصلی مقدار ۱ دارند و بقیه درایهها صفر هستند. قطر اصلی شامل اعداد ترتیبی نیست، همه اجزای ماتریس صفر نیست و مقدار بالا و پایین قطر نیز با یکدیگر برابر نیستند، بلکه فقط قطر اصلی شامل عدد ۱ است و همین ویژگی همانی بودن ماتریس را مشخص مینماید.
۲. چه شرطی برای دترمینان یک ماتریس لازم است تا آن ماتریس معکوسپذیر باشد؟
دترمینان باید منفی باشد.
دترمینان باید عددی غیر صفر باشد.
دترمینان باید برابر صفر باشد.
دترمینان باید حتما عددی صحیح باشد.
اگر دترمینان یک ماتریس صفر باشد، آن ماتریس معکوس ندارد و منفرد (singular) خواهد بود. تنها زمانی یک ماتریس معکوسپذیر است که دترمینان آن عددی غیر صفر باشد؛ بنابراین پاسخ «دترمینان باید عددی غیر صفر باشد» درست است. گزینههایی مثل «برابر صفر بودن»، «منفی بودن» یا «صحیح بودن» دترمینان باعث معکوسپذیری نمیشوند و ملاک فقط غیر صفر بودن مقدار دترمینان است.
۳. فرض کنید دستگاه AX = B را داریم و معکوس ماتریس A وجود دارد. برای یافتن X کدام روش درست است؟
جمع کردن معکوس ماتریس A به هر دو طرف معادله
ضرب هر دو طرف معادله در معکوس ماتریس A از سمت چپ
ضرب هر دو طرف معادله در معکوس ماتریس A از سمت راست
ضرب هر دو طرف معادله در ماتریس همانی (Identity Matrix)
برای حل معادله AX = B وقتی معکوس ماتریس A وجود دارد، باید هر دو طرف معادله را در معکوس A از سمت چپ ضرب کرد. زیرا ضرب معکوس از سمت چپ باعث حذف A و باقی ماندن X میشود. جمع کردن یا ضرب از سمت راست ترتیب صحیح را رعایت نمیکند و استفاده از ماتریس همانی کمکی به حل معادله نمیکند. ترتیب ضرب در ماتریسها اهمیت زیادی دارد و باید مطابق با ساختار معادله باشد.
۴. چرا یک ماتریس مربعی با دترمینان صفر نمیتواند معکوس داشته باشد؟
زیرا ضرب ماتریس و معکوس آن همیشه برابر ماتریس همانی نیست.
زیرا دترمینان صفر یعنی معادله ماتریسی جواب منحصربهفرد ندارد.
چون در این حالت همه ستونهای ماتریس باید همگی برابر باشند.
چون فقط ماتریسهای مربعی با درایههای مثبت معکوسپذیر هستند.
زمانیکه دترمینان ماتریس صفر باشد، حاصل ضرب آن با هر ماتریس دیگری (حتی اگر معکوس وجود داشت) هرگز نمیتواند برابر ماتریس همانی (Identity Matrix) شود؛ زیرا دترمینان صفر به این معنی است که معادله ماتریسی راه حل منحصربهفرد ندارد و ماتریس منفرد (Singular) است. بنابراین «دترمینان صفر یعنی معادله ماتریسی جواب منحصربهفرد ندارد» درست است، اما هیچ الزامی برای مثبت بودن درایهها یا برابر بودن ستونها در این بحث وجود ندارد، و اینکه ضرب صرفا به دست همانی نمیرسد، علت اصلی را توضیح نمیدهد.












با سلام و عرض ادب
ضمن تشکر از مطالب مفیدتون معکوس یک ماتریس 1*1 ( با یک درایه ) چگونه بدست می آید ؟
با سلام لطفا کنید بفرمایید معکوس ماتریس1*1 ( با یک دارایه [a] ) چگونه حساب می شود
عالی
ثابت کنید وارون ماتریس مرتبه دو در صورت وجود منحصر به فرد است ؟
جواب
برهان خلف
سلام ودرود
همه ی قطرهای ماتریس همانی برابر1یا فقط قطر های نزولی ماتریس همانی برابر 1؟
با سپاس همیشگی از تمام دست اندر کاران مجله ی فرادرس
درود بر شما و تشکر از راهنمایی های بی حدتان
ببخشید ماتریس چه ربطی به تابع وارن داره؟
بسیار سپاسگذارم از آموزش عالیتان. موفق باشید.
با سلام
خیلی خوب وعالی توضیح داده شده بود.ممنون ومتشکر
اگر ماتریس یک ستون داشته باشه اونوقت معکوسش چیه ؟
معکوس ماتریس فقط برای ماتریس مربعی مطرح میشه
اثبات ماتریس :
A.C).B=(C.(A.B)
اثبات ماتریس: tr( BA)= (tr(AB
با سلام
اثبات قضیه دو ماتریس A&Bمربعی و هم اندازه باشندوA منفرد باشد ثابت کنید ماتریس ABبرابر صفر و برعکس
سلام. به بخش نظرات مطلب «ماتریس غیر منفرد — به زبان ساده (+ دانلود فیلم آموزش رایگان)» مراجعه کنید.
موفق باشید.
با سلام.
اثبات قضیه اگر Aو Bدو ماتریس مربعی و هم اندازه باشند و Aمنفرد باشد انگاه دترمینانAB برابر با صفر و برعکس
اثبات اگرA معکوس پذیر باشد انگاه دترمینان Aدر دترمینانAاین ورس برابر صفر
خواهشا این رو ب من جواب بدید
سلام. آنچه نوشتهاید نادرست است. احتمالاً منظورتان این تساوی است: det(A)det(A−1)=1. با توجه به رابطه det(AB)=det(A)det(B)، اگر B=A−1، آنگاه تساوی det(AA−1)=det(A)det(A−1) را داریم. از طرفی، چون AA−1=I و det(I)=1، میتوان نتیجه گرفت: det(A)det(A−1)=det(AA−1)=det(I)=1. برای مطالعه بیشتر، به مطلب «ماتریس همانی و ماتریس یکانی | به زبان ساده» مراجعه کنید.
موفق باشید.
اثبات معکوس A×Bمیشود معکوسB در معکوس A
خواهشا اثبات این قضیه رو بفرمایید
سلام. اثبات این تساوی به صورت زیر است:
(AB)(AB)−1(A−1AB)(AB)−1(IB)(AB)−1B(AB)−1B−1B(AB)−1I(AB)−1(AB)−1=I=A−1I=A−1=A−1=B−1A−1=B−1A−1=B−1A−1
موفق باشید.
عالی بود ممنونم
عالی
اگه ماتریس آ به توان ایکس برسه،دترمینان ماتریس هم به توان ایکس میرسه؟
یعنی اگه دترمینان ماتریس آ رو به دست بیاریم
بعدش ماتریس آ رو به توان دو برسونیم
برای به دست اوردن دترمینان جدید فقط کافیه دترمینان قبلی رو هم به توان ایکس برسونیم؟
سلام. بله، یکی از خواص دترمینان این است: det(An)=det(A)n.
از همراهیتان با مجله فرادرس خوشحالیم.
خوب بود.ولی موسیقیش خیلی ازار دهندس.هیچ نیازی به اهنگ گذاشتن روی فیلما نیست
خیلی ممنون ، عالی بود ، این ویدیو و ویدیوی توضیح ماتریس برای کسانی که با ماتریس آشنایی ندارند خیلی خوبه
موسیقی فیلم آزار دهنده است.
روش آموزشیتون عالیه عالیه بی نهایت سپاسگزارم . مطالب را طوری آموزش میدهید که علاوه بر یادگیری باعث ایجاد علاقه به آن مبحث هم میشویم
خوب و آسان بود مرسی که زحمت کشیدید خصوصا شکلها که تو ذهن اثر خوب میذاره
عالی بود ممنونم
توی سایتتون گشت میزدم که با کارتون آشنا بشم
واقعا فوق العاده این
تبریک میگم و ممنونم!
خیلی مطالب و دوره های خوبی دارین
بی نظیر بوووود!
من دبیرستانی ام و همیشه فکر میکردم که ماتریس عجب چیز به درد نخوریه!
مثالتون فوق العاده بود!
سلام .اگر وارون دو ماتریس باهم برابر باشند میتونیم بگیم دو ماتریس باهم برابرند ؟ممنون میشم جواب بدین
سلام.
فرض کنید A و B دو ماتریس معکوسپذیر بوده و معکوس آنها برابر با C باشد. در این صورت، روابط AC=CA=I و BC=CB=I برقرار است که I ماتریس واحد را نشان میدهد. در نتیجه، داریم: A=AI=A(CB)=(AC)B=IB=B. بنابراین، اگر A−1=B−1، آنگاه A=B.
مرسی واقعا عالی و مفید بود. سپاس
سلام. خیلی عالی و ساده و مفید بود. خیلیممنون.
سلام. برای بذست آوردن یک ماتریس 1*3 چه نوع ماتریسهایی را باید در هم ضرب کنیم.
سلام
فقط مهم اینه که مارتیس اول سه سطر داشته باشه و ماتریس دوم یک ستون و تعداد ستون ماتریس اول با تعداد سطر ماتریس دوم برابر باشه.
مثلا:
ماتریس اول سه در یک و ماتریس دوم یک در یک
یا
ماتریس اول سه در دو و ماتریس دوم دو در یک
یا
ماتریس اول سه در سه و ماتریس سه دو در یک
در همه این حالت ها ماتریس نهایت سه در یک خواهد بود.
با سلام. اگر بخواهیم معکوس یک ماتریس را به پیمانهی یک عدد دیگر به دست آوریم باید چطور عمل کنیم؟( البته برای محاسبه ی معکوس ماتریس به پیمانه ی یک عدد به روش الحاقی رو بلدم – اما مثلا برای یک روش تکراری یا روش دیگر چطور باید این کار را انجام داد؟)با تشکر
نشان دهید وارون یک ماتریس بالا مثلثی،بالامثلثی است.ممنونم اگرجواب این سوال رو بدید
عالی بود مرسی مثال ماتریس ها خیلی قشنگ بود من معلم ام و از این نوع بیان ماتریس لذت بردن