تنش صفحه ای (Plane Stress) و معادلات تبدیل آن – آموزش جامع
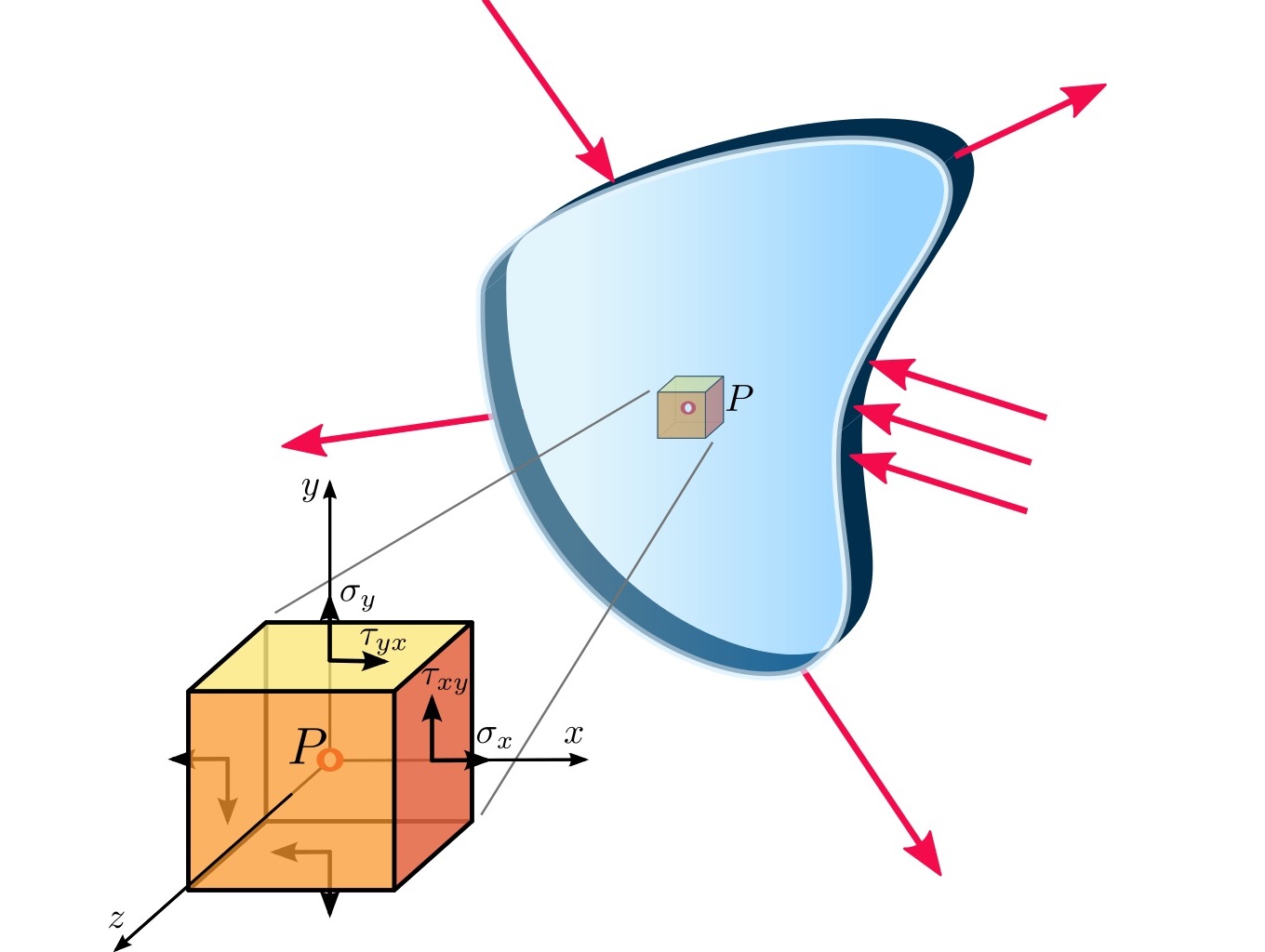
«تنش صفحهای» (Plane Stress)، یکی از حالتهای دوبعدی تنش است که در آن تمام مؤلفههای تنش درون یک صفحه قرار دارند. این نوع تنش هنگامی رخ میدهد که یکی از سه تنش اصلی در المان مورد تحلیل برابر با صفر باشد. در این مقاله، شما را با مفهوم تنش صفحهای، تنشهای موجود بر روی مقاطع دوران یافته، معادلات تبدیل و حالتهای خاص این نوع تنش آشنا خواهیم کرد. در انتها نیز به تشریح چند مثال کاربردی خواهیم پرداخت.
تنش صفحهای بر روی المانهای کوچک
برای آشنایی با نحوه عملکرد تنش صفحهای، المان زیر را در نظر بگیرید. اندازه این المان بسیار کوچک است. محورهای xyz با گوشههای المان موازی و بر سطوح آن عمود هستند. برای نامگذاری صفحات این المان از یک قاعده مخصوص استفاده میکنیم.
به عنوان مثال، صفحه سمت راست المان در شکل زیر، صفحه مثبت x و صفحه سمت چپ آن، صفحه منفی x است. به این ترتیب، سطح بالایی المان، صفحه مثبت y و سطح جلویی آن، صفحه مثبت z خواهد بود.
هنگامی که یک جسم در معرض تنش صفحهای xy قرار میگیرد، مؤلفههای تنش تنها بر روی صفحات x و y المان مورد نظر و موازی با راستای محوریهای x و y اعمال میشوند. این حالت تنش بر روی سطح تمام اجسام تحت بارگذاری، به جز در نقاط اعمال بارهای خارجی قابل مشاهده است.
قواعد نامگذاری و علامتگذاری
اندیس تنش نرمال (σi)، بیانگر صفحه اعمال تنش است. به عنوان مثال، تنش σx بر روی صفحه x المان و تنش σy بر روی صفحه y المان اعمال میشوند. بر اساس فرض کوچک بودن اندازه المان، تنشهای موجود بر روی صفحات روبهرویی با هم برابر هستند.
علامت تنشهای نرمال بر اساس قاعده زیر تعیین میشود:
- علامت تنش فشاری، مثبت است.
- علامت تنش کششی، منفی است.
تنش برشی (τij) دارای دو اندیس است. اندیس اول (i)، صفحه اعمال تنش و اندیس دوم (j) جهت اعمال تنش را نمایش میدهد. به عنوان مثال، تنش برشی τxy بر روی صفحه x قرار دارد و در راستای محور y اعمال میشود. به همین ترتیب، تنش برشی τyx بر روی صفحه y قرار دارد و در راستای محور x اعمال میشود.
قاعده علامتگذاری تنشهای برشی به صورت زیر است:
- در صورتی که تنش برشی بر روی یکی از صفحات مثبت المان در راستای مثبت یک محور اعمال شود، علامت تنش مثبت خواهد بود. به عنوان مثال، تنشهای τxy و τyx بر روی صفحات مثبت x و y (صفحات بالا و سمت راست در المان زیر)، دارای علامت مثبت هستند.
- اگر تنش برشی بر روی یکی از صفحات مثبت المان در راستای منفی یک محور اعمال شود، علامت تنش منفی خواهد بود.
- در صورتی که تنش برشی بر روی یکی از صفحات منفی المان در راستای منفی یک محور اعمال شود، علامت تنش مثبت خواهد بود. به عنوان مثال، تنشهای τxy و τyx بر روی صفحات منفی x و y (صفحات پایین و سمت چپ در المان زیر)، دارای علامت مثبت هستند.
- اگر تنش برشی بر روی یکی از صفحات منفی المان در راستای مثبت یک محور اعمال شود، علامت تنش منفی خواهد بود.
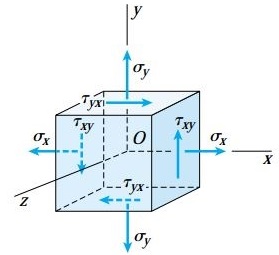
برای به خاطر سپردن راحتتر قاعده علامتگذاری تنش برشی، توجه داشته باشید که اگر جهتهای مرتبط با اندیسهای تنش برشی به صورت مثبت-مثبت یا منفی-منفی باشند، علامت تنش مثبت و اگر به صورت مثبت-منفی یا منفی-مثبت باشند، علامت تنش منفی خواهد بود. قاعده علامتگذاری تنشهای برشی با وضعیت تعادل المان مطابقت دارد. تنشهای برشی موجود بر روی صفحات رو به رویی در یک المان بسیار کوچک باید دارای مقادیر برابر و جهتگیری مخالف باشند. بر این اساس، جهتگیری تنش مثبت τxy بر روی یک صفحه مثبت، رو به بالا و بر روی یک صفحه منفی، رو به پایین خواهد بود.
علاوه بر این، میدانیم که تنشهای برشی در صفحات عمود برابر هستند و جهتگیری آنها به گونهای است که هر دو تنش به سمت یک نقطه نزدیک یا از آن دور میشوند. این نقطه بر روی تقاطع دو صفحه عمود بر هم قرار دارد. بنابراین داریم:
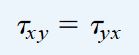
به منظور راحتی بیشتر در رسم المانهای تنش صفحهای، معمولاً فقط نمای دوبعدی این المانها رسم میشود. این روش برای نمایش تمام تنشهای اعمال شده بر المان کافی خواهد بود اما باید به خاطر داشت که المان مورد بررسی، یک جسم جامد با ضخامتی مشخص در راستای عمود بر صفحه است.
تنش بر روی مقاطع دوران یافته
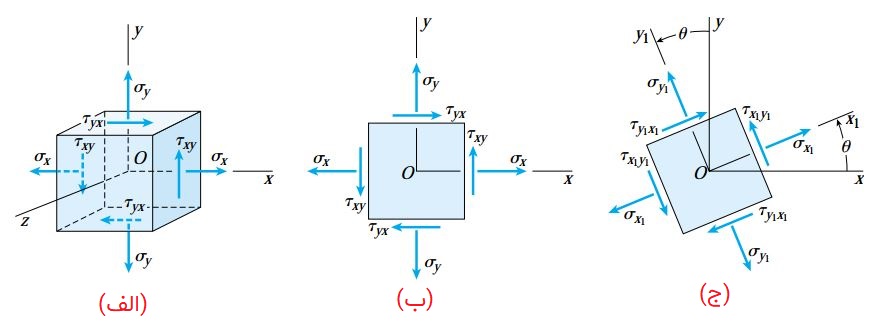
اکنون میتوانیم با فرض مشخص بودن تنشهای σy ،σx و ?xy، تنشهای اعمال شده بر روی مقاطع دوران یافته را تعیین کنیم (شکل زیر). برای به نمایش درآوردن تنشهای اعمال شده بر روی مقاطع دوران یافته، یک المان تنش جدید را بر روی محل قرارگیری المان اصلی در نظر گرفته میشود.
اگرچه، المان جدید دارای سطوح موازی و عمود بر راستای دوران است. y1 ،x1 و z1 محورهای مختصات مربوط به المان جدید هستند. در این سیستم جدید، محور z1 بر روی محور z قرار دارد و x1y1 تحت زاویه θ نسبت به xy به صورت پادساعتگرد دوران یافته است.

تنشهای نرمال و برشی اعمال شده بر روی المان جدید با حروف σy1 ،σx1 و ?x1y1 نمایش داده میشوند. قواعد علامتگذاری و نامگذاری این تنشها مشابه قواعد اشاره شده در بخش قبلی است. رابطه به دست آمده برای تنشهای برشی، در مورد المان دوران یافته نیز صدق میکند:
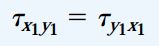
با در نظر گرفتن معادله بالا و معادلات تعادل المان میتوان مشاهده کرد که با تعیین تنش برشی اعمال شده بر روی یکی از صفحات المان در حالت تنش صفحهای، تنشهای برشی اعمال شده بر روی تمامی صفحات مشخص میشوند. با استفاده از معادلات تعادل میتوان تنشهای اعمال شده بر روی المان دوران یافته x1y1 را با توجه به تنشهای اعمال شده بر روی المان xy بیان کرد. به این منظور، یک المان گوهای شکل با صفحهای به موازات محور x1 در نظر گرفته میشود (شکل زیر). دو صفحه دیگر این المان با محوری x و y موازی هستند.
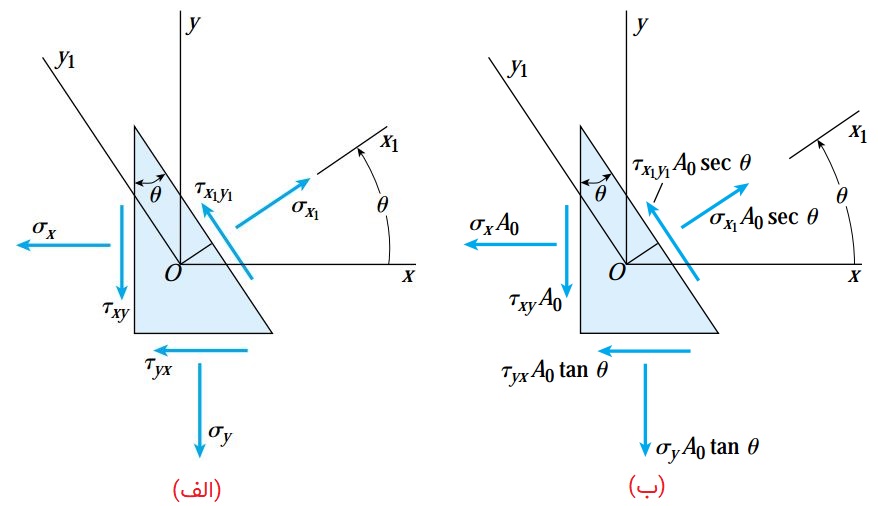
به منظور نوشتن معادلات تعادل برای این گوه، ابتدا نمودار جسم آزاد آن را مطابق شکل بالا رسم میکنیم. مساحت صفحه سمت چپ گوه (جهت منفی x) را به عنوان A0 در نظر میگیریم. با توجه به نمودار جسم آزاد، نیروهای نرمال و برشی اعمال شده بر روی آن سطح با σxA0 و ?xyA0 برابر هستند. مساحت صفحه پایینی (جهت منفی y) با A0tanθ و مساحت صفحه زاویهدار با A0secθ برابر است. بنابراین، نیروهای نرمال و برشی اعمال شده بر روی این صفحات دارای مقادیر و جهتهای نشان داده شده در شکل زیر هستند.
نیروی اعمال شده بر روی صفحات سمت چپ و پایینی گوه را میتوان به مؤلفههای عمود بر هم در راستای x1 و y1 تجزیه کرد. با جمع نیروهای موجود در این دو راستا، دو معادله تعادل به دست میآید. جمع نیروهای همراستا با x1 خواهیم داشت:
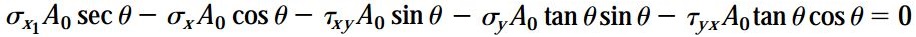
به همین ترتیب، با جمع نیروهای همراستا با y1 خواهیم داشت:
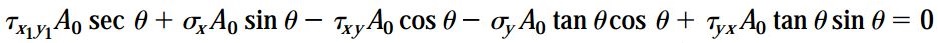
با استفاده از معادله ?xy=?xy و سادهسازی روابط بالا، دو رابطه زیر به دست میآید:
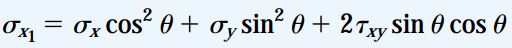
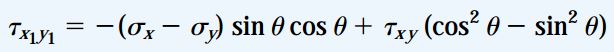
روابط بالا، با استفاده از زاویه θ و تنشهای σy ،σx و ?xy بر روی صفحات x و y، تنشهای نرمال و برشی اعمال شده بر صفحه x1 را نمایش میدهند. اگر θ=0 باشد، σx1=σx و ?x1y1=?xy خواهد بود. به علاوه، در صورتی که θ=90 باشد، σx1=σy و ?x1y1=-?xy=-?yx خواهد بود. در حالت دوم، از آنجایی که در هنگام θ=90 محور x1 به صورت عمود درمیآید، تنش ?x1y1 در هنگام اعمال بر روی صفحه سمت چپ مثبت میشود. در عین حال، تنش ?xy به سمت راست اعمال خواهد شد. در نتیجه، رابطه ?x1y1=-?yx برقرار خواهد بود.
معادلات تبدیل تنش صفحهای
با استفاده از روابط مثلثاتی میتوان معادلات تنشهای اعمال شده بر روی مقطع دوران یافته را به صورت سادهتر بیان کرد. به این منظور، در بخش زیر برخی از روابط مورد نیاز برای سادهسازی معادلات تنشها آورده شده است:

با جایگذاری روابط بالا در معادلات تنشهای اعمال شده بر مقاطع دوران یافته، خواهیم داشت:
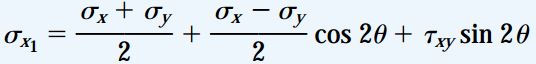
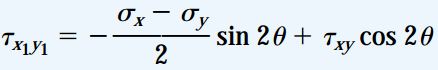
از آنجایی که این معادلات، مؤلفههای تنش را از یک دستگاه مختصات به دستگاه دیگر تبدیل میکنند، به آنها معادلات تبدیل تنش صفحهای گفته میشود. اگرچه، حالت ذاتی تنش در نقطه مورد بررسی همیشه یکسان است و به دستگاه مختصات مورد استفاده برای نمایش تنشهای اعمال شده بر روی المان بستگی ندارد.
معادلات تبدیل تنها از معادلات تعادل المان به دست میآیند. به همین دلیل، این معادلات برای تعیین تنشهای اعمال شده بر روی تمام مواد (خطی یا غیرخطی، الاستیک یا غیر الاستیک) مناسب هستند. در معادلات تبدیل میتوان نکته مهمی را در مورد تنشهای نرمال مشاهده کرد. در بخش قبلی دیدیم که با جایگذاری θ+90 به جای θ، تنش نرمال σy1 بر روی صفحه y1 در المان دوران یافته تعیین میشود. به این ترتیب، معادله زیر برای محاسبه σy1 به دست میآید:
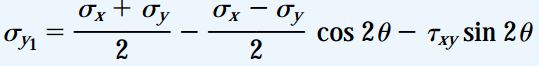
با جمع کردن σx1 و σy1، رابطه زیر برای تنش صفحهای حاصل میشود:
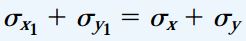
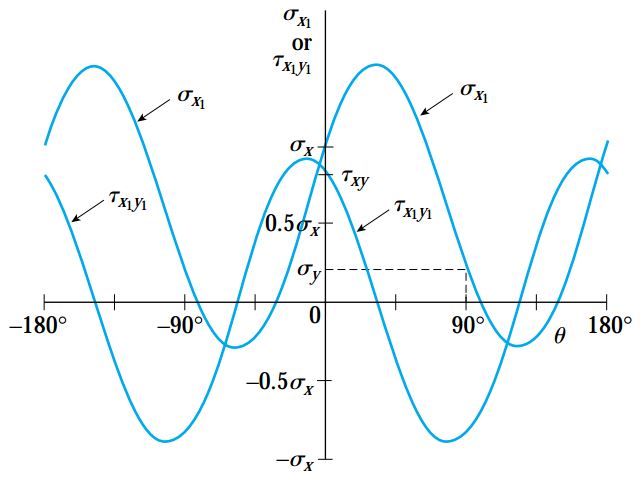
رابطه بالا نشان میدهد که حاصل جمع تنشهای نرمال اعمال شده بر روی صفحات عمود بر هم در المانهای تنش صفحهای، مقداری ثابت است و به زاویه θ بستگی ندارد. شکل زیر، نحوه تغییرات تنشهای نرمال و برشی را به صورت نمودار σx1 یا ?x1y1 در مقابل زاویه θ نمایش میدهد. این نمودار برای حالت σy=0.2σx و ?yx=0.8σx رسم شده است. همان طور مشاهده میشود، با تغییر جهت المان، مقدار تنشها نیز به طور پیوسته تغییر میکنند. در زوایای خاص، تنش نرمال به یک مقدار حداکثری یا حداقلی میرسد. در برخی از زوایا نیز این تنش برابر با صفر میشود. این شرایط برای تنش برشی نیز صادق است.
حالتهای خاص تنش صفحهای
در شرایط خاص، حالت کلی تنش صفحهای به حالتهای سادهتر تبدیل میشود. به عنوان مثال، اگر تمام تنشهای اعمال شده بر روی المان xy، به جز تنش نرمال σx، صفر باشند، المان تحت «تنش تکمحوری» (Uniaxial Stress) قرار خواهد داشت.
معادلات تبدیل برای این حالت به صورت زیر خواهند بود:
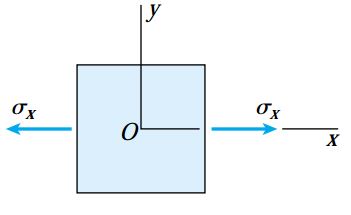
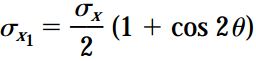

روابط بالا با معادلات به دست آمده در بخش قبلی مطابقت دارند. با این تفاوت که در این روابط از مفهوم کلیتر تنشهای اعمال شده بر روی صفحه دوران یافته استفاده شده است. یکی دیگر از حالتهای خاص تنش صفحهای، «برش خالص» (Pure Shear) است (شکل زیر). در این حالت، معادلات تبدیل با جایگذاری σx=0 و σy=0 در معادلات تبدیل اصلی به دست میآیند:



حالت خاص دیگر برای تنش صفحهای، «تنش دومحوری» (Biaxial Stress) است (شکل زیر). در این حالت، المان xy در راستای x و y تحت تنشهای نرمال قرار میگیرد. با این وجود، هیچ تنش برشی به این المان وارد نمیشود. برای به دست آوردن معادلات تبدیل در حالت تنش دومحوری تنها باید عبارات دارای ?yx را از معادلات تبدیل اصلی حذف کرد:


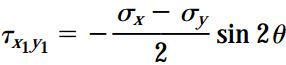
تنش دومحوری در سازههای متعددی نظیر مخازن فشار جدار نازک رخ میدهد.
مثالهای مبحث تنش صفحهای
برای درک بهتر مطالب ارائه شده در این مقاله، به تشریح دو مسئله مرتبط با تنش صفحهای میپردازیم.
مثال 1
یک المان تحت تنش صفحهای را در نظر بگیرید (شکل زیر). مقادیر تنشهای وارد شده به این المان به صورت زیر است:
- σx = 16000 psi
- σy = 6000 psi
- ?yx = ?xy = 4000 psi
با توجه به اطلاعات بالا، تنشهای اعمال شده بر روی المان دوران یافته تحت زاویه 45 درجه را تعیین کنید.
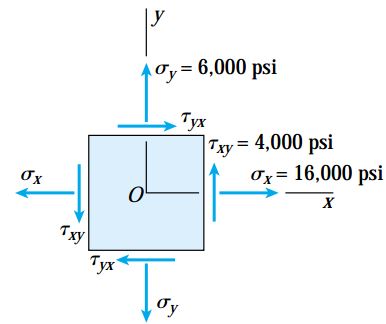
برای تعیین تنشهای اعمال شده بر روی المان دوران نیافته از معادلات تبدیل استفاده میکنیم. با توجه به اطلاعات مسئله، مقادیر مربوط به عبارتهای زیر را به دست میآوریم:
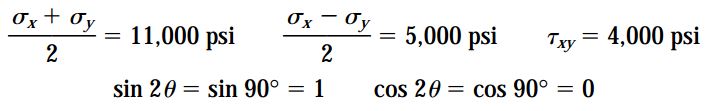
با جایگذاری مقادیر بالا در معادلات تبدیل خواهیم داشت:
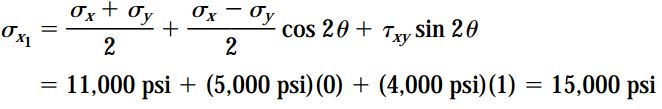

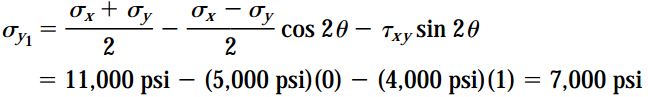
به این ترتیب، حالت تنش المان دورانیافته مانند شکل زیر خواهد بود.
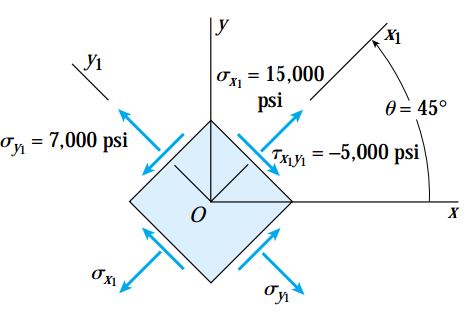
با استفاده از نتایج به دست آمده میتوان تنشهای اعمال شده بر روی تمام وجوه المان دوران یافته را به راحتی محاسبه کرد. توجه داشته باشید که تمامی تنشهای برشی دارای مقادیر یکسانی هستند. به علاوه، حاصل جمع تنشهای نرمال ثابت بوده و برابر با 22000psi است.
مثال 2
بر روی نقطهای از یک سازه تحت بارگذاری، شرایط تنش صفحهای حاکم است. شکل زیر، مقادیر تنش و جهتگیری آنها در المان تنش نقطه مورد نظر را نمایش میدهد. با توجه به اطلاعات مسئله، مقادیر تنشهای اعمالش ده بر روی المان دوران یافته تحت زاویه 15 درجه ساعتگرد نسبت به المان اولیه را محاسبه کنید.
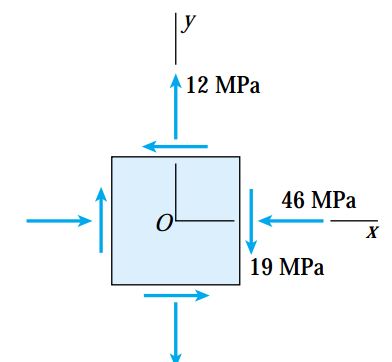
با توجه به شکل بالا، مقادیر تنشهای اعمال شده بر المان اصلی به صورت زیر هستند:
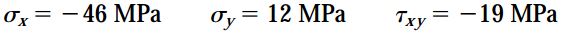
شکل زیر، المان دوران یافته تحت زاویه 15 درجه ساعتگرد را نمایش میدهد. در این المان، محور x1 نسبت به محور x دارای زاویه 15- درجه است (این زاویه را میتوان به صورت 75+ درجه نیز در نظر گرفت).
با استفاده از معادلات تبدیل میتوان تنشهای اعمال شده بر روی صفحه x1 در المان دوران یافته را به راحتی محاسبه کرد. برای انجام این محاسبات در ابتدا باید مقادیر زیر را به دست آورد:
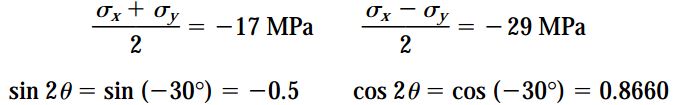
با جایگذاری مقادیر بالا در معادلات تبدیل داریم:
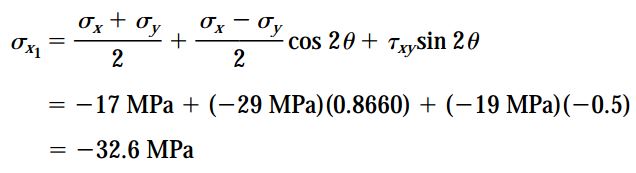
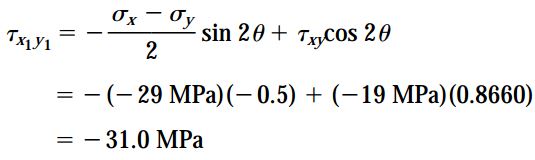
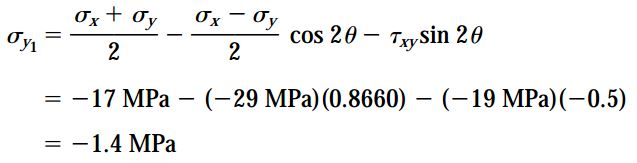
به این ترتیب، حالت تنش المان دورانیافته مانند شکل زیر خواهد بود.
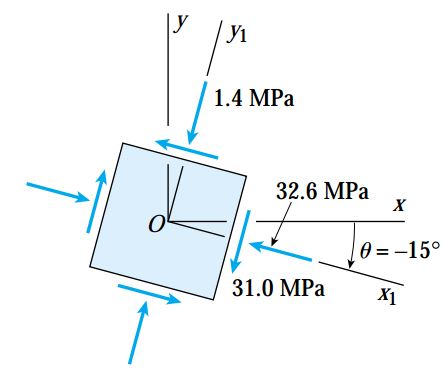
^^













سلام.خیلی ممنون از زحمتی که برای نوشتن این مقالات میکشید.به نظر من بعضی از مطالب گفته نشده،مثل تنش اصلی،کرنش اصلی و …این چیز ها.اگر اونها رو هم بهش اضافه کنید خیلی عالی میشه.تشکر
سلام، وقت شما بخیر؛
در بخش مثالهای کاربردی (مثال 1)، مفهوم کرنش اصلی مورد بررسی قرار گرفته است. برای آشنایی بیشتر با مفهوم تنش اصلی، مطالعه مقالات زیر را به شما پیشنهاد میکنیم:
تنش اصلی و تنش برشی ماکسیمم — آموزش جامع
آشنایی با تبدیلات تنش — مبانی مقاومت مصالح
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.