دسته بند فازی (Fuzzy Classifier) – به زبان ساده
به عنوان یک ابزار کاربردی در حوزه «یادگیری ماشین نظارت شده» (Supervised machine Learning)، «دسته بندهای» (Classifier) مختلفی به کار گرفته میشود. به این ترتیب «دسته بند فازی» (Fuzzy Classifier) را میتوان نوعی دستهبند معرفی کرد که براساس «مجموعههای فازی» (Fuzzy Sets) یا «منطق فازی» (Fuzzy Logic) عمل میکند. مفهوم مجموعههای فازی در این دستهبند، هم در مرحله آموزش و هم شیوه عملکرد مورد استفاده قرار میگیرد.
در این نوشتار به بررسی دستهبند فازی میپردازیم و خصوصیات آن را مورد بررسی قرار میدهیم. البته شایان ذکر است که در مورد دستهبندهای بیز نیز مطلب آشنایی دسته بند بیز ساده — مفاهیم اولیه و کاربردها در وبلاگ فرادرس منتشر شده است. همچنین برای آشنایی با منطق فازی و مجموعههای آن میتوانید مطلب منطق فازی (Fuzzy Logic) و کاربردهای آن — به زبان ساده و مجموعه فازی (Fuzzy Set) — به زبان ساده را مطالعه کنید. البته خواندن مطلب اعتبار سنجی متقابل (Cross Validation) — به زبان ساده نیز خالی از لطف نیست.
دسته بند فازی
در «یادگیری ماشین» (Machine Learning)، دستهبند (Classifier) در اصطلاح به الگوریتمی گفته میشود که براساس خصوصیات و ویژگیهای مشاهدات و نمونهها، برچسبهایی را که مرتبط با دسته یا کلاسها هستند به هر عضو از مشاهدات نسبت میدهد. به این ترتیب با ایجاد الگویی که الگوریتم به کار میبرد، قادر است برای مشاهدات جدید، برچسب یا میزان تعلق به دسته یا گروه را پیشبینی یا تعیین کند. واضح است که برچسبها بیانگر شماره گروه یا دسته است، در نتیجه میتوانند مقدار آن عضوی از اعضای مجموعه اعداد طبیعی باشد.
در چنین الگوریتمهایی، ویژگیهای مربوط به مشاهدات به صورت برداری از متغیرها ثبت و مورد استفاده قرار میگیرند. در بیشتر مواقع، الگوریتمهای دستهبندی با استفاده از توابع فاصله عمل تفکیک و ردهبندی را انجام میدهند. به این ترتیب فاصله بین هر مشاهده از نماینده هر گروه یا دسته میتواند ملاکی برای تعیین برچسب آن باشد. البته الگوریتمهای دیگری مانند «درخت تصمیم» (Decision Tree) که عمل دستهبندی را انجام میدهند، ممکن است براساس توابع فاصله عمل نکنند و از «الگوهای منطقی» (Logical Paradigm) بهره ببرند.
معمولا برای اندازهگیری میزان خطای الگوریتمهای دستهبندی، مشاهدات را به دو گروه «آموزشی» (Training) و «آزمایشی» (Test) تقسیم میکنند. به کمک دادههای آموزشی، مدل ساخته شده و براساس آن دادههای آزمایشی دستهبندی میشوند. میزان مطابقت برچسبهای حاصل از اجرای مدل روی دادههای آزمایشی با برچسبهای واقعی مشاهدات، میزان دقت یا خطای الگوریتم دستهبند را مشخص میکند. همچنین برای تنظیم پارامترهای مدل دستهبندی ممکن است از تکنیک اعتبار سنجی متقابل نیز استفاده شود. به هر حال آنچه در انتهای اجرای الگوریتمهای دستهبندی حاصل میشود، برچسبهایی است که برای نقاط یا مشاهدات بدست میآید و تعلق آنها را به هر گروه آشکار میسازد. با توجه به خصوصیات و شکل دادهها و مشاهدات ممکن است از الگوریتمهای متفاوتی برای دستهبندی استفاده شود. در این مطلب خصوصیاتی که مربوط به الگوریتم دستهبند فازی هستند و برچسبهای حاصل از دستهبندی فازی مورد بررسی قرار گرفتهاند.
- برچسبهای منعطف (Soft Labeling): از اصول اولیه در «دستهبندی» (Classification) و «تشخیص الگو» (Pattern Recognition)، «جدا بودن» (Disjoint) دستهها از یکدیگر است. به این معنی که هیج مشاهدهای نمیتواند همزمان به بیش از یک دسته تعلق داشته باشد. به الگوریتمهایی که چنین برچسبهایی ایجاد میکنند «دستهبند غیرمنعطف» و برچسبهای آن را «شکننده» (Crisp Labeling) گفته میشود. در مقابل دستهبندهای فازی برای هر مشاهده بیش از یک دسته یا گروه منظور کرده و برای تعلق هر مشاهده به گروه یا دسته، «درجه عضویت» (Membership Degree) در نظر میگیرند، درست مانند منطق فازی که برای درستی یک گزاره درجهای از درستی قائل میشود. به همین جهت چنین الگوریتمهایی را «دستهبند فازی» (Fuzzy Classifier) مینامند. به این ترتیب برچسبهای حاصل را «نرم» (Soft Labeling) مینامند. در نتیجه هر مشاهده با درجات یا مقدارهای مختلف میتواند به بیش از یک دسته یا گروه تعلق داشته باشد.
با توجه به این امر، میتوان دستهبندی فازی را به صورت «تابعی تخمینگر» (Approximator Function) در نظر گرفت که براساس مجموعه ویژگیها، برچسبهایی با وزنهایی در فاصله تولید کند. این گزاره را به صورت زیر با نماد ریاضی نشان میدهیم.
در عبارت بالا، فضای حاصل از ویژگیها است. همچنین نیز تعداد کلاسها را نشان میدهد. در نتیجه حاصل اجرای الگوریتمهای دستهبند فازی برای هر مشاهده، برداری است که دارای سطر بوده و درایههای آن مقداری در فاصله هستند. به این ترتیب مقدار این بردار مشخص میکند که مشاهده با چه میزان یا درجه عضویتی به دسته یا گروه ام تعلق دارد.
نکته: در الگوریتمهای دستهبندی غیرمنعطف، میتوان تابع را به صورت زیر در نظر گرفت. به این ترتیب وزنها یا مقدار ۰ یا ۱ خواهند بود.
زمانی که ایجاد توابع تخمینگر بوسیله روشها یا الگوریتمهای دستهبند دیگر به سختی صورت میگیرد، الگوریتم دستهبندی فازی به خوبی عمل کرده و نتیجهای قابل تفسیر و مناسب ایجاد میکند.

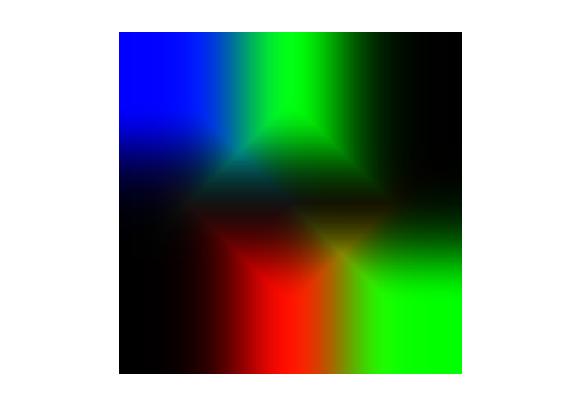
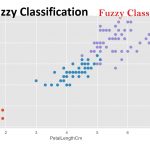
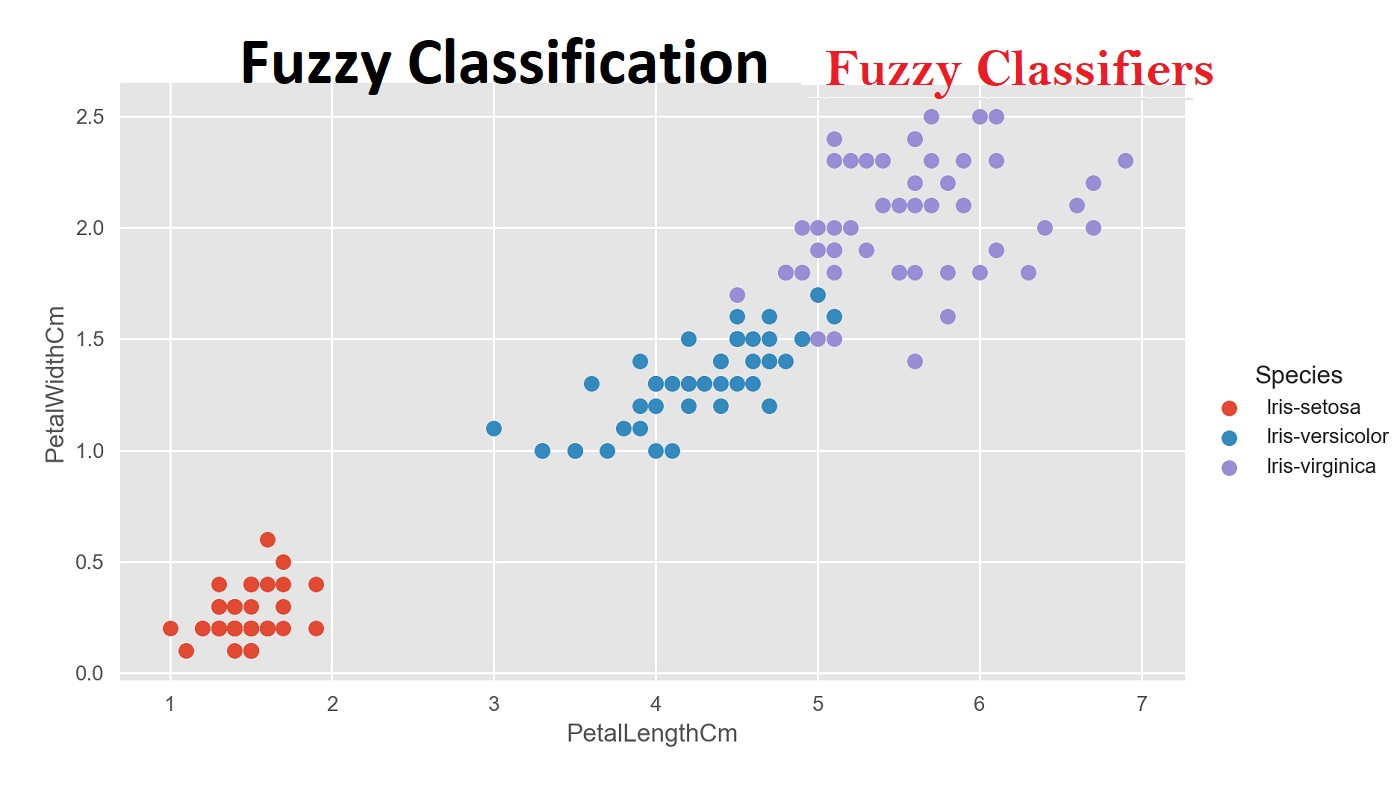
در تصویرهای ۱ و ۲، سه گروه یا دسته در نظر گرفته شدهاند. در تصویر ۱، از الگوریتمهای غیرمنعطف استفاده شده و برچسبها به نظر شکننده میرسند. به این معنی که مرز مشخصی بین گروهها یا دستهها وجود دارد. در حالیکه در تصویر ۲ با استفاده از الگوریتمهای دستهبند فازی، برچسبها منعطف بود و با درجات مختلف، هر مشاهده ممکن است به بیش از یک دسته تعلق داشته باشد. کاملا مشخص است که رنگهای تفکیک کننده، در مرزها با یکدیگر مخلوط شدهاند.
- تفسیرپذیری: همانطور که منطق فازی نسبت به تفکر و منطق ارسطویی یا دو دویی، به درک و شیوه تفکر بشر نزدیکتر است، نتایج حاصل از دستهبند فازی نیز بهتر قابل درک هستند زیرا امکان محصور یک مشاهده در دو گروه یا دسته به طور همزمان را در نظر میگیرند. این در حالی است که در دستهبندهای غیرمنعطف، این الگو لحاظ نمیشود و تفسیر آن مشکل و گاهی غیرممکن است.
- اندازه نمونه کوچک و استفاده از تجربیات: در دستهبندهای فازی میتوان از نظر متخصصین برای دستهبندی نیز استفاده کرد. در نتیجه هم مشاهدات (دادهها) و نظر خبرگان در اجرای دستهبندی دخیل است. به این ترتیب با الگوگیری از نظر خبرگان میتوان دستهبندی فازی را برای اندازه نمونههای کوچک نیز اجرا کرد. برای مثال تعیین فرد در دستههای بیماریهای نادر یا فعالیتهای تروریستی، به کمک الگوریتمهای دستهبند فازی حتی با مشاهدات و نمونههای آموزشی محدود نیز به خوبی عمل میکنند.
به منظور درک بهتر دستهبند فازی به تصاویر زیر دقت کنید. در تصویر ۳ پیشبینی هوا براساس احتمال یا درجه عضویت صورت گرفته است. به این ترتیب مشخص است که فردا با درجه عضویت بارانی، با درجه عضویت ابری، با درجه عضویت با وزش باد و با درجه آفتابی است. در حالیکه در تصویر شماره ۴، وضعیت هوا با قاطعیت بارانی گزارش شده است.
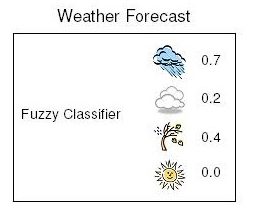

نکته: همانطور که میبینید ممکن است در مدل فازی، مجموع درجه عضویتها برابر با ۱ نباشد در حالیکه در مدلهای برمبنای احتمال، این شرط وجود دارد که مجموع احتمالات برای پیشامدهای فضای احتمال باید برابر با ۱ باشد. بنابراین حتی اگر مدلهای غیرمنعطف را بر مبنای احتمال به صورت برچسبهای نرم و مدلهای منعطف درآورد باز هم مدلی به صورت فازی نخواهند بود.
مدلهای دستهبندهای فازی
در ادامه این بخش به بررسی دو گونه دستهبند فازی با نامهای «دستهبندهای فازی قاعده- محور» (Fuzzy Rule-Based Classifiers) و «دستهبندهای فازی الگو-محور» (Fuzzy Prototype-Based Classifiers) خواهیم پرداخت. هر یک از این گونهها در زمینههای تخصصی به کار گرفته میشوند.
دستهبندهای فازی قاعده-محور (Fuzzy Rule-Based Classifiers)
یکی از سادهترین دستهبندهای فازی، استفاده از سیستمهای «اگر-آنگاه» (If-Then) است. چنین سیستمهایی در کنترلهای فازی نیز به کار گرفته میشود. برای مثال دو ویژگی (مسئله دو متغیره) را در نظر بگیرید که هر یک مقدارهای عددی دارند. همچنین فرض کنید قرار است این مشاهدات به سه گروه یا طبقه با برجسبهای ۱، ۲ و ۳ تفکیک شوند. یک سیستم یا الگوریتم دستهبند فازی از نوع قاعده-محور، ممکن است براساس قوانینی مانند زیر، عمل برچسبگذاری را انجام دهد.
هرچند متغیرها یا ویژگیهای و عددی هستند ولی قاعدهها براساس مقادیر غیرعدد یا «مقادیر کلامی» (Linguistic Values) مشخص شدهاند. اگر تعداد مقادیر کلامی برابر با و تعداد ویژگیها نیز باشند، تعداد حالاتی که برای ایجاد ترکیبهای عطفی لازم داریم تا سیستم قاعدههای «اگر-آنگاه» ساخته شود، برابر است با . در اینجا به عنوان «مقادیر کلامی» سه عبارت در نظر گرفته شده است که شامل ، و هستند.
اگر در تکنیک دستهبندی همه حالات ممکن برای شکلگیری ترکیبات عطفی، در نظر گرفته شده باشد، عمل برچسبگذاری تبدیل به یک مدل «جدول جستجو» (Look-up Table) میشود. در حالیکه در دستهبند فازی، همه حالتهای ممکن منظور نشده و فقط براساس بعضی از قواعد و ترکیبات سیستمهای «اگر-آنگاه» عمل کرده و میتواند براساس الگوریتم دستهبند فازی، تصمیماتی را ایجاد کنند که در قاعدههای موجود قرار نداشته است. به این شکل، ترکیبی از مقادیر کلامی در قاعده تصمیم به کار میرود که از قبل وجود نداشته.
هر یک از مقدارهای کلامی به صورت یک تابع عضویت بیان میشود. به تصویر ۵ دقت کنید. در این تصویر، تابع عضویت برای مقدار کلامی تعیین شده است.
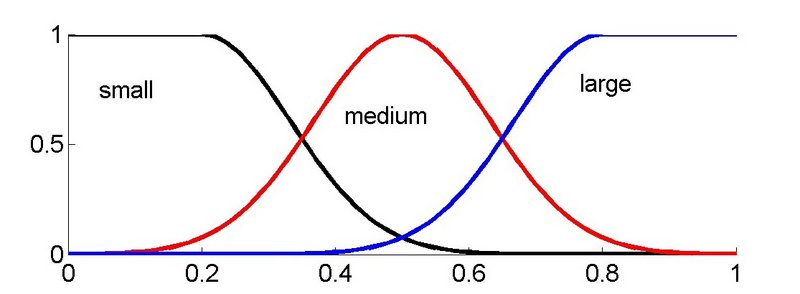
تصویر شماره ۵، نواحی مربوط به تغییر قاعده را مشخص میکند. برای مثال اگر مقدار تا حدود باشد، مقدار کلامی برابر با است. در این صورت حدود و کرانهای در بازه حدود تا قرار گرفته و از آن به بعد مقدار کلامی، برابر با است.
به این ترتیب میتوان قانون شماره ۱ (Rule 1) را در مثال قبل به صورت تابع نشان داد.
به این علت مقدار کلامی را با اندیس بالای و مشخص کردهایم تا نشان دهیم مقدار برای متغیر متفاوت با برای متغیر است. از طرفی عملگر AND نیز مشابه پیدا کردن مقدار حداقل است. البته میتوان از های دیگر مثل نرم مثلثی که مانند عملگرهای منطقی در منطق فازی به کار گرفته میشوند، نیز استفاده کرد. به این ترتیب میتوان را به عنوان وزن رای داده شده در قاعده اول برای دسته در نظر گرفت.
برای پیدا کردن مقدار خروجی دستهبند فازی کافی است که آراء همه قواعد را با هم تجمیع کنیم. تکنیکهای متفاوتی برای عمل تجمیع وجود دارد. برای مثال فرض کنید که از «پیدا کردن حداکثر» (Maximum Aggregation Method) به عنوان روش تجمیع استفاده کنیم. اگر بردار را در نظر بگیریم، برچسب نرم برای مشاهده شامل مقادیر عضویت است که در بازه تغییر میکند. در ضمن باید توجه داشت که بیانگر شماره گروه یا دسته است و داریم که تعداد کل دستهها یا گروهها است.
فرض کنید قاعده رای به کلاس داده باشد در نتیجه رابطه زیر برقرار است.
همانطور که دیده شد، برآیند و نتیجه اجرای الگوریتم دستهبندی فازی در این وضعیت، برچسبها بودند. به این نوع الگوریتمها «برآیند برچسب کلاس» (Class label as the consequent) میگویند. در مقابل این نوع الگوریتمها حالتی نیز وجود دارد که برچسبهای کلامی به عنوان نتیجه اجرای الگوریتم حاصل میشود. برای مثال سیستم «اگر-آنگاه» به شکل زیر را در نظر بگیرید.
به نظر میرسد که این نوع استنتاج توسط هوش انسانی بهتر عمل میکند. این نوع دستهبندها براساس «سیستم فازی از نوع ممدانی» (Mamdani-type Fuzzy System) عمل میکنند. خروجی نیز به صورت برچسبهای نرم است که برای تشخیص دستهها به کار میرود.
از طرفی ممکن است نتیجه یک دستهبند فازی به صورت ترکیبی از توابع محاسباتی باشد. در این حالت دستهبند فازی از (Takagi-Sugeno fuzzy systems) بهره میگیرد. به این ترتیب یک سیستم فازی دستهبندی با این الگو، میتواند به شکل زیر باشد.
| IF is and AND is AND ... AND is THEN AND |
در این رابطه، ها همان مقادیر کلامی هستند همینطور نیز ضرایب مدل محسوب میشوند. یک مدل ساده در این حالت میتواند با در نظر گرفتن مقدار ثابت برای هر کلاس یا دسته حاصل شود. در این صورت شکل استنباط برای دستهبند فازی به صورت زیر در خواهد آمد.
واضح است که در اینجا ها مقادیر ثابت برای هر دسته هستند. به این ترتیب در چنین مدلی، همه قواعد برای همه کلاسها به کار میرود و نتایج آراء تابع دستهبند، محاسبه میشود. ممکن است با کمک «تجمیعکننده حداکثر» (Maximum Aggregation Method) که در قبل به آن اشاره شد، محاسبات انجام شده و مجموع نتایج برای همه قواعد حاصل شود.

روش دیگر برای تجمیع در چنین حالتی استفاده از میانگین وزنی (Weighted Mean) است. رابطه زیر نتیجه آراء را برای کلاس یا دسته نشان میدهد. واضح است که بیانگر ضریب ثابت برای کلاس یا دسته برای قانون است.
یک سوال اصلی در دستهبندهای قاعده-محور، چگونگی آموزش دادن آنها است. همچنین باید به چگونگی تعیین توابع عضویت برای مقدارهای کلامی نیز توجه کرد. تعیین برآیندها نیز از چالشهای مهم این دستهبندها است. چندین روش برای آموزش و تنظیم پارامترهای دقیق چنین مدلهایی وجود دارد که از جمله آنها میتوان به «شبکههای عصبی فازی» (Fuzzy Neural Networks) و «الگوریتمهای ژنتیک» (Genetic Algorithm)، اشاره کرد. برخی از طبقهبندیهای فازی قاعده-محور از ترکیب قوانین زیادی تشکیل شده و پیچیده شدن مدل، باعث افت کارایی آن میشود. زیرا این قوانین براساس دادههای آموزشی تهیه شده ولی کارایی لازم برای تشخیص الگوی دادههای آزمایشی را ندارند.
دستهبندهای فازی الگو-محور (Fuzzy Prototype-Based Classifiers)
بعضی از مدلهای دستهبندی فازی، الهام گرفته از ایده فازیسازی روی مدلهای دستهبندی استاندارد و عادی ایجاد شدهاند. یکی از شاخصترین مدلهای دستهبندی کلاسیک، «-نزدیکترین همسایه» (K-Nearest Neighbor) است که در آن هر مشاهده براساس نزدیکترین همسایه برچسبگذاری میشود. محاسبه برآورد احتمال پسین، برای دستهها به شکل خام و براساس نسبت اعضای کلاس به کل بدست میآید. در الگوریتم فازی KNN از توابع فاصله استفاده شده و برچسبهای نرم نیز براساس همسایهها تعیین میشوند.
قواعد ترکیبی فازی برای ادغام دستهبندها
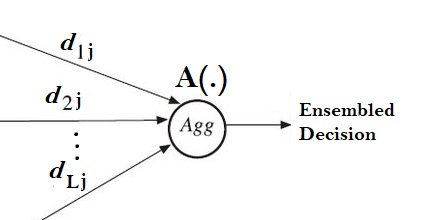
در «سیستمهای دستهبند چندگانه» (Multiple Classifier System)، نتایج حاصل از تصمیمات چندین دستهبند، تجمیع شده تا یک تصمیم یا برجسبهای (از نوع نرم یا شکننده) ایجاد شود. فرض کنید یک مشاهده و تابع عضویت برای دستهبند ام باشدکه کلاس یا دسته را برای آن مشاهده در نظر گرفته است. واضح است که در اینجا مقادیر به تعداد دستهبندها و به تعداد کلاسها محدود میشود. بنابراین اگر تعداد کل دستهبندها و نیز بیانگر تعداد کلاسها باشد، میتوان ماتریسی در نظر گرفت که درایههای آن باشند. به چنین ماتریسی، «نمایه تصمیمگیری» (Decision Profile) برای مشاهده گفته میشود.
نکته: بسیاری از چنین ماتریسیهایی توسط برآورد احتمال پسین برای کلاس یا دستهها تولید میشوند و به نوعی برچسبهای نرم ایجاد میکنند.
برمبنای تصمیمات فازی میتوان «توابع تجمیع فازی» (Fuzzy Aggregation Function) نیز ایجاد کرد. میزان درجه عضویت مشاهده در دستهبندام برای کلاس یا دسته بوسیله درایههای مربوط به سطر ام و ستون ام ماتریس نمایه تصمیمگیری مشخص میشود. به این ترتیب میتوانیم درجه تعلق مشاهده را به دسته یا گروه با تابع به صورت زیر تعیین کنیم.
با توجه به ساختار تابع ، باید دامنه و برد آن به شکل زیر باشد.
تابع یا روش تجمیع را میتوان «حداکثر» (Maximum)، «حداقل» (Minimum) یا «میانگین» (Mean) مقادیر درایههای سطرهای یک ستون در نظر گرفت.
نکته: اندیس در بیانگر ترکیبی یا گروهی (Ensemble) بودن این درجه عضویت است.
اگر مطلب بالا برای شما مفید بوده، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای تصویر و پردازش سیگنال
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- مجموعه آموزشهای برنامهنویسی پایتون
- مجموعه آموزشهای یادگیری ماشین و بازشناسی الگو
- آموزش تخمین خطای طبقه بندی یا Classifier Error Estimation
- رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS
- دسته بند بیز ساده (Naive Bayes Classifiers) — مفاهیم اولیه و کاربردها
^^













با سلام
مطالب مفیدی برای ورود به این حوزه است که به دقت نوشته شده بودند.
خدا قوت…