تحلیل تشخیص خطی فیشر (Fisher’s Linear Discriminant) – پیاده سازی در پایتون

در بیشتر موارد به منظور حل مسائل ساده، الگوریتم‌های مختلف «یادگیری ماشین» (Machine Learning) با استفاده از تکنیک‌ها مختلف به جواب واحدی می‌رسند. ولی بوسیله بعضی از تبدیلات، می‌توان سرعت و دقت انجام عملیات یادگیری ماشین را بهبود بخشید. در این نوشتار به بررسی یکی از این تبدیلات به نام «تحلیل تشخیص خطی فیشر» (Fisher's Linear Discriminant) می‌پردازیم و از آن برای حل مسائل یادگیری ماشین بهره می‌بریم.

از آنجایی که آنالیز یا تحلیل تشخیص خطی فیشر، الهام گرفته از یکی دیگر از ابتکارات دیگر این دانشمند آمار یعنی «تحلیل واریانس» (Analysis of Variance) است، با خواندن مطلب تحلیل واریانس (Anova) — مفاهیم و کاربردها پیش‌نیازهای لازم برای این نوشتار را کسب خواهید کرد. همچنین در این نوشتار به مفاهیم احتمال پسین و پیشین برخورد خواهیم کرد. برای آشنایی بیشتر با این مفاهیم بهتر است مطلب احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده را از قبل مطالعه کرده باشید. همچنین خواندن متن تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده و بردار ویژه و مقدار ویژه — از صفر تا صد نیز خالی از لطف نیست.

تحلیل تشخیص خطی فیشر (Fisher's Linear Discriminant)

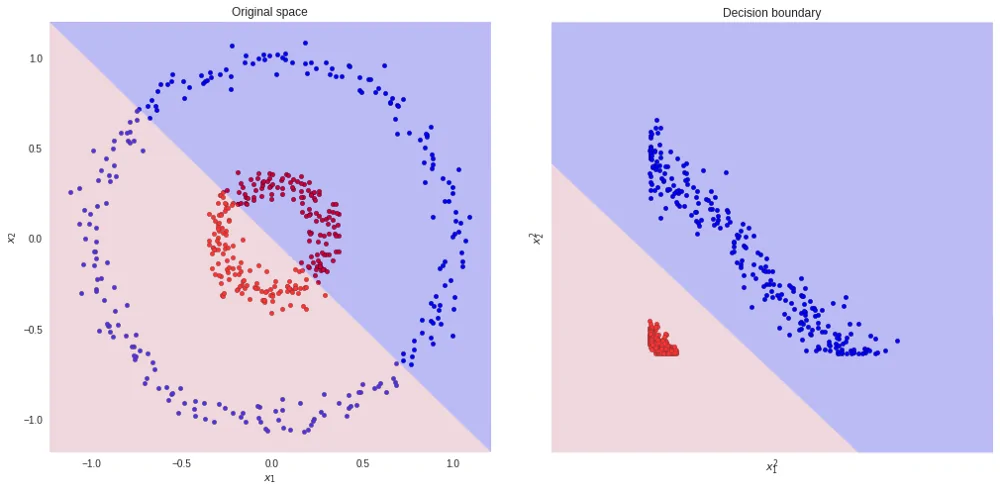
یکی از روش‌های حل مسائل «دسته‌بندی» (Classification)، کاهش ابعاد مسئله به منظور ساده‌تر شدن و رسیدن سریع‌تر به جواب است. برای مثال فرض کنید که در یک فضای دو بعدی (K=2) باید به بررسی و تفکیک نقطه‌های دو بعدی با رنگ‌های قرمز و آبی بپردازیم. به تصویر زیر توجه کنید.

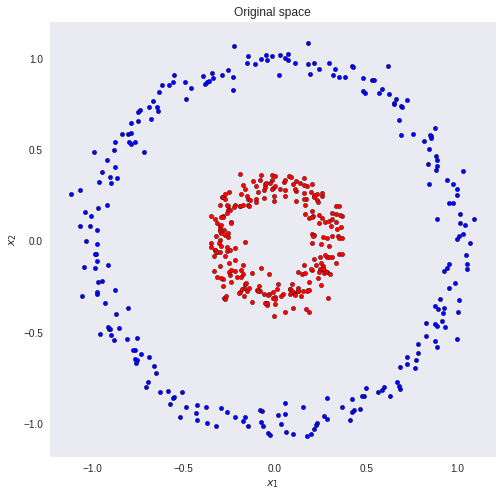
باید بتوانیم الگوی نقاط آبی و قرمز را شناخته و امکان تشخیص محل قرارگیری نقطه‌ای جدید در دسته آبی یا قرمز را کسب کنیم. یکی از روش‌ها مرسوم برای انجام این کار «تحلیل تشخیص خطی فیشر» (Fisher's Linear Discriminant) یا به اختصار FLD است. اگر مسئله بالا را به صورت یک «مسئله خطی» (Linear Problem) در نظر بگیریم، مشخص است که امکان دریافت پاسخ صحیح را از مدل نخواهیم داشت. زیرا رابطه خطی بین نقاط و دسته‌ها وجود ندارد. ولی اگر بتوانیم این داده‌ها را طوری تبدیل کنیم که بتوان نقاط را بوسیله یک خط تفکیک کرد، به جواب بهینه خواهیم رسید.

برای مثال اگر داده‌ها مربوط به هر بعد از مشاهدات را به صورت مربع درآوریم، به راحتی می‌توان با رسم یک خط، دو گروه را تفکیک کرد. به تصویرهای زیر دقت کنید. ناحیه آبی و صورتی در زمینه تصویرها، بیانگر ناحیه تشخیصی برای مشاهدات است. به مجموعه مقادیر روی محور عمودی و افقی در نمودار سمت چپ توجه کنید.

از آنجایی که نمودار ترسیم شده در سمت چپ، دایره‌ای است، می‌توان حدس زد، تبدیلاتی که به صورت مربع هستند، می‌توانند مناسب باشند. ولی سوالی که می‌توان مطرح کرد این است که اگر داده‌ها چند بعدی باشند و امکان ترسیم نقاط وجود نداشته باشد، چگونه می‌توان تبدیل مناسب را تشخیص داد؟

کاهش بعد مسئله

یکی از راه‌حل‌های مسائل مربوط به دسته‌بندی، کاهش بعد است. فرض کنید که با یک مسئله با بعد D مواجه هستید. یعنی تعداد ویژگی‌ها (متغیرها) مرتبط با مسئله برابر با D است. منظور از کاهش بعد، تبدیل داده‌ها به بعدی مثل 'D است در آن داریم $$D < D'$$. در این حالت D بعد اصلی داده‌ها و 'D بعد پس از تصویر (Projection) یا تبدیل کردن (Transformation) داده‌ها است.

اگر مسئله به یک بعد کاهش یابد، براساس یک مقدار آستانه مثل t می‌توان دسته‌ها را به صورت زیر براساس مشاهدات x ایجاد کرد.

• اگر مقدار متغیر پاسخ y بزرگتر یا مساوی با t باشد، نقطه x به کلاس ۱ (C1) تعلق دارد.
• در غیر اینصورت x در کلاس C2 است.

در اینجا توجه داشته باشید که متغیر پاسخ (y) به صورت ترکیب خطی از متغیرها (x) و وزن (W) است. در این حالت می‌نویسیم. توجه داشته باشید که منظور $$W^T$$‌ ترانهاده بردار وزن‌ها (W) است.

$$\large y =W^Tx$$

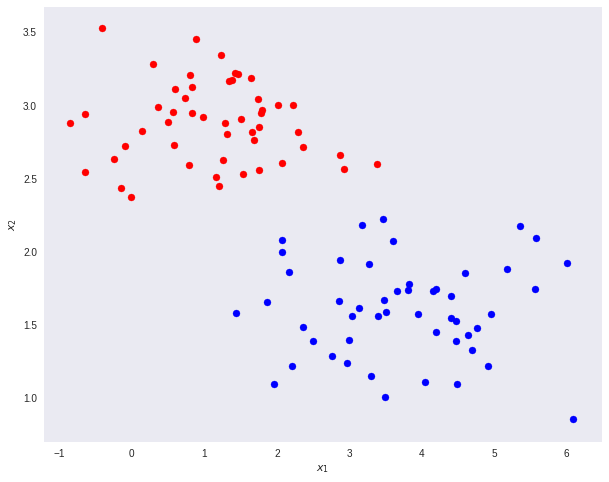
فرض کنید داده‌های دو بعدی متعلق به دو کلاس مطابق تصویر زیر وجود دارند. می‌خواهیم با استفاده از تبدیل T بعد مسئله را از D=2 به D'=1 برسانیم.

$$\large T(V): R^2 \rightarrow R$$

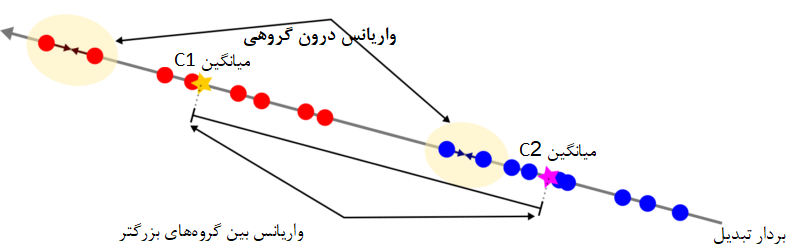
برای شروع لازم است میانگین دسته‌های یک و دو را محاسبه کنیم. به این ترتیب مرکز ثقل یا تمرکز داده‌های هر دو گروه مشخص می‌شود. این میانگین‌ها را $$m_1$$ و $$m_2$$ نام‌گذاری می‌کنیم. در اینجا فرض شده که دسته اول با C1 و دسته دوم با C2 مشخص شده و هر یک به ترتیب دارای $$N_1$$ و $$N_2$$ نقطه هستند.

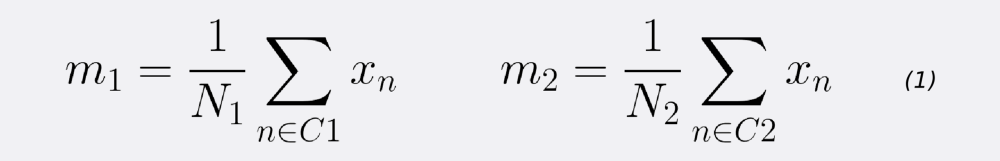
به این ترتیب براساس میانگین هر کلاس، سعی می‌کنیم کلاس‌ها را بازیابی کنیم. به معنی دیگر می‌خواهیم با استفاده از بردار وزن W میانگین دو کلاس را به یکدیگر متصل کنیم.

نکته: زمانی که کاهش بعد اتفاق می‌افتد، مقداری اطلاعات از بین خواهد رفت. در این مسئله توجه داشته باشید که هر دو کلاس کاملا مجزا هستند و می‌توان بوسیله یک خط، بدون تغییر بعد، آن‌ها را از یکدیگر تمیز داد.

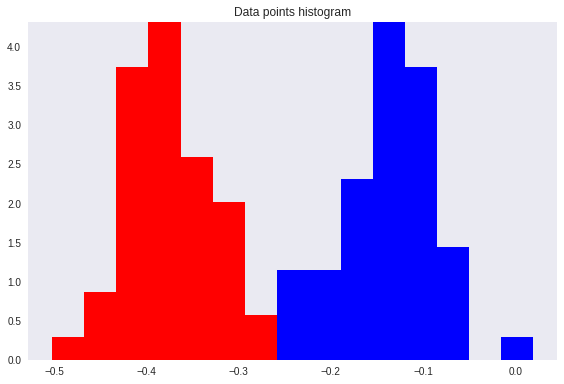
اگر این نقاط را با یک تبدیل، در یک بعد نمایش دهیم، مشخص است که تعدادی از نقاط با یکدیگر همپوشانی پیدا می‌کنند (ناحیه زرد رنگ) و تشخیص تمایز بین کلاس‌ یا دسته‌ها مشکل‌تر می‌شود.

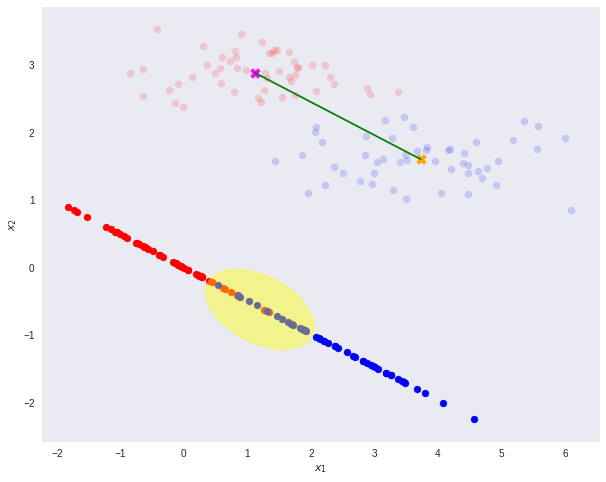
این همپوشانی، در نمودار فراوانی یا هیستوگرام نیز قابل مشاهده است.

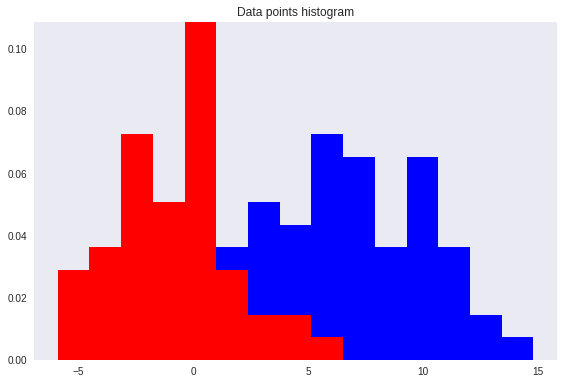
درست در همین جا است که «تحلیل تشخیص خطی فیشر» به کار می‌آید. ایده‌ای که فیشر برای حل چنین مسئله‌ای ارائه داد، استفاده از تابعی بود که باعث حداکثر سازی فاصله میانگین‌های کلاس‌ها شود و در عین حال واریانس درون کلاس‌ها را کمینه سازد. با این کار، میزان همپوشانی کلاس‌ها بسیار کاهش خواهد یافت. به بیان دیگر FLD، تبدیلی را انتخاب یا معرفی می‌کند که بیشترین تمایز یا میزان تشخیص را ایجاد کند. این کار بوسیله بیشینه‌سازی نسبت واریانس بین گروهی و درون گروهی صورت می‌پذیرد. به این ترتیب در صورت و مخرج این نسبت دو مولفه یا مشخصه داریم:

• فاصله (واریانس) بین گروه‌ها که باید حداکثر شود
• پراکندگی (واریانس) درون دسته‌ها که باید کمینه شود.

نکته: مقدار بزرگ برای واریانس بین کلاس‌ها، به معنی آن است که میانگین کلاس‌ها تا حد امکان از یکدیگر دور هستند. در مقابل کوچک بودن واریانس درون کلاس‌ها، بیانگر نزدیک بودن نقاط تبدیل یافته در هر کلاس است.

به منظور تشخیص تابع تبدیل $$T(V)$$، روش FLD، براساس تابع $$J(W)$$ که در زیر مشخص شده است، بردار وزن‌ها را تعیین می‌کند.

$$\large J(W)=\dfrac{(m_2-m_1)^2}{S_1^2+S_2^2}$$

مشخص است که رابطه‌های زیر در این مورد باید در نظر گرفته شوند.

$$\large y_n=W^Tx_n$$

$$\large s^2_k=\sum_{n\in C_k}(x_n-m_k)^2$$

اگر تابع $$J(W)$$ را به صورت برداری و به شکل زیر بنویسیم، به کمک مشتق‌گیری برحسب $$W$$‌، مقدار بهینه (ماکزیمم) برای این تابع حاصل خواهد شد.

$$\large J(W)=\dfrac{W^TS_BW}{W^TS_WW}$$

مشخص است که صورت این کسر همان پراکندگی بین گروه‌ها و مخرج نیز پراکندگی درون گروه‌ها است. جواب این مسئله مطابق با رابطه‌ای است که در ادامه قابل مشاهده است.

$$\large W \propto S^{-1}_W(m_2-m_1)$$

به این ترتیب می‌توان تفکیک بسیار مناسبی براساس مقدار یک آستانه مثل t ایجاد کرد.

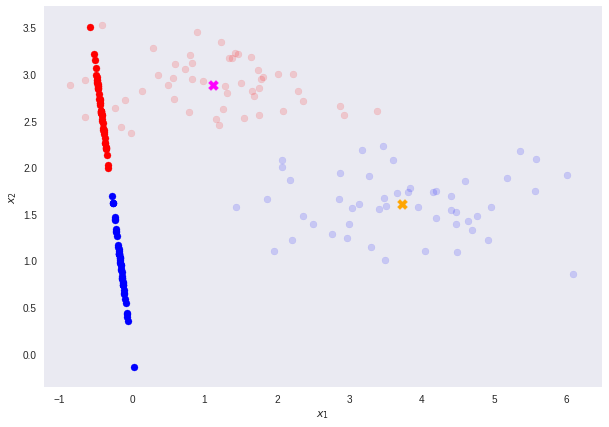
این تفکیک به کمک نمودار فراوانی یا هیستوگرام نیز به خوبی قابل تشخیص است.

تحلیل تشخیص خطی فیشر برای چندین گروه

می‌توان به راحتی تحلیل FLD را به چندین گروه ($$K>2$$) تعمیم داد. در اینجا از ماتریس کوواریانس بین و درون گروهی استفاده خواهیم کرد. به این ترتیب رابطه‌ها به صورت زیر نوشته خواهند شد.

$$\large S_W =\sum_{k=1}^K S_k$$

$$\large S_k =\sum_{n \in C_k}(x_n-m_k)(x_n-m_k)^T$$

$$\large S_B =\sum_{k=1}^K N_k(m_k-m)(m_k-m)^T$$

$$\large W =\max _{D'}(eign (S^{-1}_{W}S_B))$$

باید توجه داشت که در اینجا عبارت‌های $$S_W$$ ماتریس کوواریانس درون گروهی و $$S_B$$ نیز ماتریس کوواریانس بین گروهی را نشان می‌دهند. به این ترتیب بردار $$W$$ به صورت ماکزیمم مقادیر ویژه ماتریس $$S^{-1}_WSB$$ روی ابعاد مختلف $$D'$$ حاصل می‌شود. برای مثال اگر بخواهیم یک مسئله با مجموعه داده با بعد $$D=784$$ را به $$D'=2$$ تبدیل کنیم، بردار $$W$$ از دو مقدار که هر کدام بزرگترین مقادیر ویژه در هر بعد هستند، ایجاد خواهد شد.

ایجاد یک تشخیص خطی فیشر

تا به حال از تحلیل FLD برای کاهش بعد استفاده کردیم، ولی در این مرحله با استفاده از این تکنیک، می‌خواهیم داده‌های D-بعدی مربوط به توزیع چند متغیره نرمال برای K کلاس یا دسته مختلف را که به صورت مخلوط شده هستند، دریافت کرده و آن‌ها را تفکیک کنیم.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

یعنی تشخیص دهیم که هر کدام از نقاط به کدام توزیع متعلق است.

تابع چگالی احتمال توزیع نرمال چند متغیره با بردار Dبعدی میانگین $$\mu$$ و ماتریس کوواریانس $$\Sigma_{D\times D}$$ به صورت زیر نوشته می‌شود.

$$\large N(X|\mu, \Sigma)=\dfrac{1}{(2\pi)^\frac{D}{2}}\dfrac{1}{|\Sigma|^{\frac{1}{2}}}\exp \{-\frac{1}{2}(X-\mu)^T\Sigma_{-1}(X-\,u)\}$$

واضح است که منظور از $$|\Sigma|$$، دترمینان ماتریس کوواریانس است. این مقدار نشان می‌دهد که به چه میزان فضای داده‌ها فشرده یا گسترده هستند. برای انجام محاسباتی که در بخش قبل به آن پرداختیم، در حالت نرمال چند متغیره از کد پایتون که در زیر قابل مشاهده است، استفاده می‌کنیم.

با استفاده از این برنامه، مقدارهای پارامترهای توزیع نرمال چند متغیره (یعنی $$\mu$$ و $$\Sigma$$) برای دسته‌های $$k=1,2,\cdots,K$$ براساس داده‌های تبدیل یافته، برآورد می‌شود. به این ترتیب به کمک محاسبه نسبت مجموعه داده‌های آموزشی در هر دسته (خط ۱۱ از کد)، می‌توان احتمال پیشین (Prior Probability) را که احتمال تعلق هر داده به دسته kام را نشان می‌دهد، بدست آورد. با این کار با توجه به رابطه‌ای که بین احتمال پیشین و پسین در قضیه بیز وجود دارد، تابع شرطی چگالی مشاهدات به شرط دسته‌ها ($$p(x|Ck)$$ برای دسته‌های مختلف $$k=1,2,\cdots,K$$ قابل محاسبه خواهد بود.

به این منظور ابتدا داده‌ها را کاهش بعد داده از بعد D به 'D تبدیل می‌کنیم. لازم به یادآوری است که در این مرحله باید $$D'$$ باشد. آنگاه رابطه مربوط به تابع چگالی توزیع نرمال چند متغیره را برای هر داده تبدیل شده، محاسبه می‌کنیم. سپس احتمال شرطی $$P(C_k|x)$$ را که احتمال پیشین است، به کمک رابطه زیر، برای همه دسته‌ها مورد محاسبه قرار می‌دهیم.

$$\large P(C_k|x)=p(x|C-k)P(C_k)$$

این محاسبه در خط ۸ کد زیر انجام شده است.

به این ترتیب نقطه‌هایی که دارای بزرگترین احتمال پسین برای دسته k هستند، به آن گروه تعلق می‌گیرند و در واقع، عمل دسته‌بندی صورت خواهد گرفت.

انجام تحلیل روی داده‌های MNIST

در این قسمت، از داده‌های آزمایشی MNIST که مربوط به بانک اطلاعاتی اسباب‌بازی‌ها است، استفاده می‌کنیم. قرار است که ابعاد این مسئله که به صورت $$D=784$$ است را به $$D'=2$$ برسانیم. میزان دقت در این تبدیل حدود 56٪ است. اگر فضا را به ۳ بعد برسانیم، دقت به حدود ۷۴٪ خواهد رسید. با استفاده از این دو تبدیل می‌توان مقادیر را توسط نمودارها، بهتر نمایش داد.

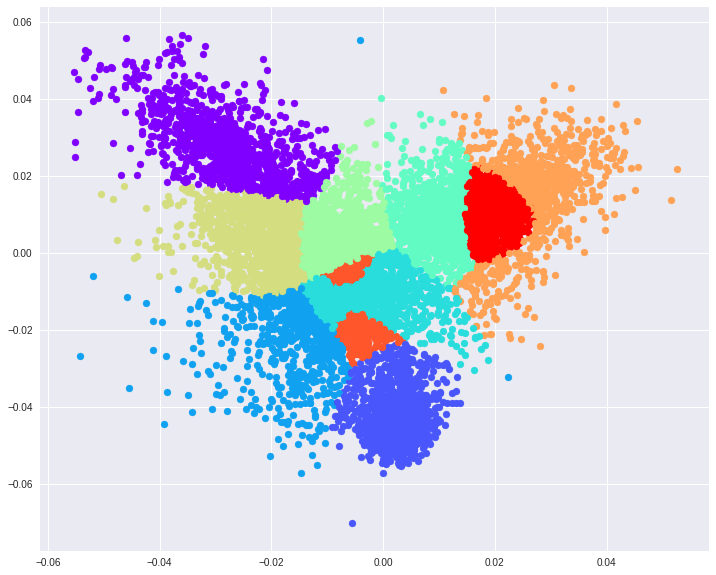
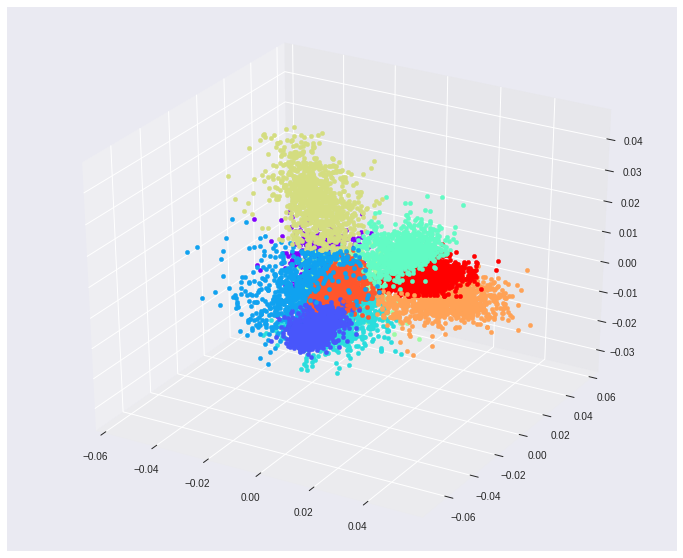
نکاتی که باید در این نوشتار به آن توجه داشت، در زیر فهرست شده‌اند.

• تشخیص خطی فیشر، در اصل یک روش کاهش بعد است ولی نمی‌توان آن را به عنوان روش تشخیصی کامل در نظر گرفت.
• به کمک تحلیل تشخیص خطی فیشر، برای دسته‌بندی دو دویی (Binary Classification)، می‌توان به نقطه آستانه بهینه‌ای مثل t رسید که مبنای دسته‌بندی داده‌ها باشد.
• برای داده‌های چند گروهی، می‌توان از مدل احتمال شرطی نرمال چند متغیره استفاده کرد.
• برای داده‌های چند گروهی، احتمال پسین و پیشین براساس قانون یا قضیه بیز قابل محاسبه هستند.
• برای تعیین جهت بهینه برای تبدیل داده‌ها، روش فیشر احتیاج به داده‌های برچسب‌دار (برچسب به معنی شماره هر گروه یا دسته است) دارد تا بتواند بهترین بردار ضرایب یا بهترین تبدیل را ایجاد کند. به همین دلیل، این روش در مسائل «یادگیری ماشین» برای تکنیک‌های «یادگیری نظارت شده» (Supervised Learning) مناسب است.
• اگر داده‌ها D بعدی باشند، به کمک روش توضیح داده شده، حداکثر بعد داده‌های تبدیل یافته D-1 خواهد بود.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های بهینه سازی چند هدفه
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• گنجینه آموزش های محاسبات هوشمند
• آموزش یادگیری ماشین
• احتمال شرطی (Conditional Probability) — اصول و شیوه محاسبه

^^