انتگرال کانولوشن و محاسبه آن — به زبان ساده (+ دانلود فیلم آموزش رایگان)

کانولوشن، یک تکنیک بسیار قدرتمند و کارآمد برای محاسبه پاسخ حالت صفر (یعنی پاسخ به ورودی هنگام شرایط اولیه صفر) یک سیستم به هر ورودی دلخواه با استفاده از پاسخ ضربه است. کانولوشن، خاصیت خطی و جمع آثار یا برهم‌نهی دارد. در این آموزش، درباره «انتگرال کانولوشن» (Convolution Integral) بحث خواهیم کرد.

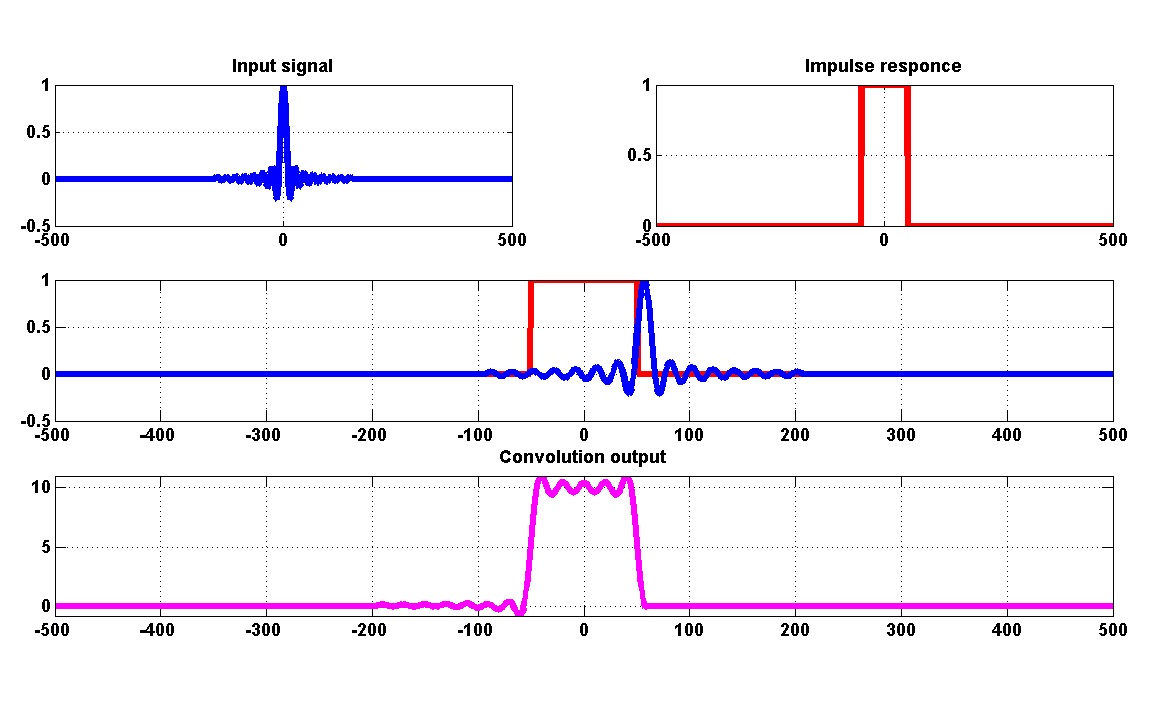
برای درک این روش، سیستمی را در نظر بگیرید که با معادله دیفرانسیل زیر توصیف شده است:

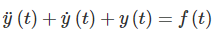
که در آن، $$y(t)$$ خروجی و $$f(t)$$ ورودی است. پاسخ ضربه ($$h(t)$$) این سیستم را می‌توان به‌صورت زیر محاسبه کرد:

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

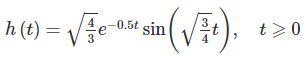
شکل پاسخ ضربه به‌صورت زیر است:

اگر ورودی $$f(t)$$ یک سیگنال شناخته شده مانند پله، ضربه یا سینوسی باشد، پیدا کردن خروجی $$y(t)$$ کار آسانی است. اما اگر ورودی کمی پیچیده‌تر باشد، برای محاسبه خروجی باید چه‌کار کنیم؟ با استفاده از کانولوشن، می‌توان پاسخ ورودی‌های پیچیده‌تر مانند شکل زیر را تعیین کرد. در واقع، با استفاده از کانولوشن می‌توان خروجی هر سیگنال ورودی را با دانستن پاسخ ضربه محاسبه کرد.

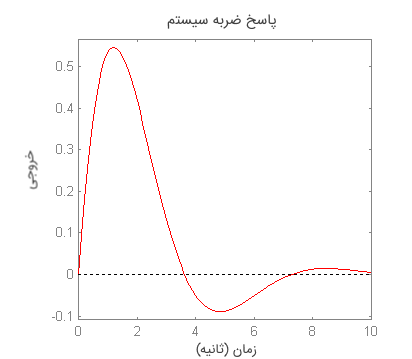
فرض کنید می‌خواهیم ورودی زیر را به سیستمی اعمال کنیم.

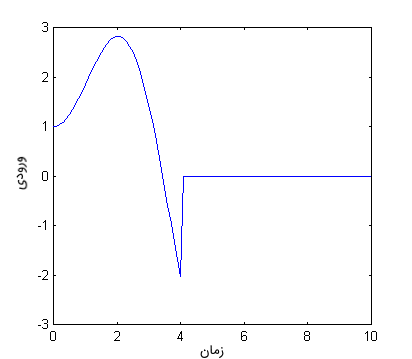
برای درک بهتر نحوه عملکرد کانولوشن، تابع پیوسته بالا را به‌عنوان یک تابع گسسته نشان می‌دهیم که هر 0.8 ثانیه از ورودی نمونه‌برداری شده است. شکل زیر ورودی گسسته تقریبی را نشان می‌دهد.

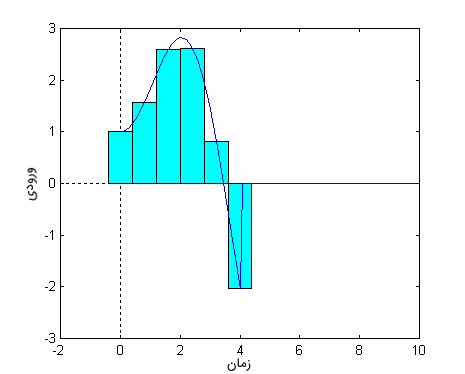
تقریب شکل بالا را می‌توان یک گام جلوتر برد و هر مستطیل را مطابق شکل زیر با یک ضربه نشان داد. مساحت هر ضربه، برابر با مساحت مستطیل متناظر است.

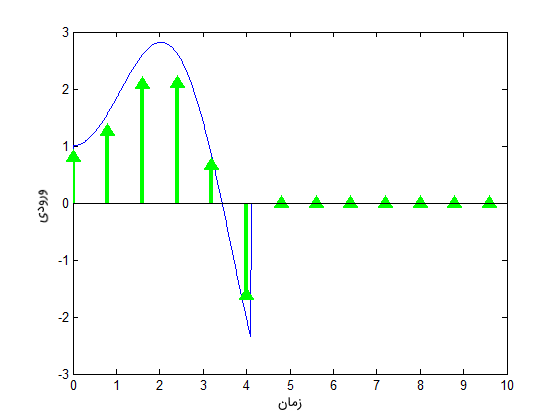
اصل جمع آثار بیان می‌کند که پاسخ سیستم به رشته‌ای از ضربه‌ها برابر با مجموع پاسخ به تک تک آن‌ها است. پاسخ سیستم به هریک از این ضربه‌ها در شکل زیر قابل مشاهده است:

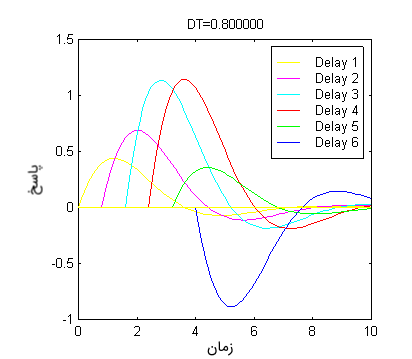
با توجه به شکل بالا، می‌توان نکات زیر را بیان کرد:

• $$h(t)$$، پاسخ سیستم به ضربه واحد $$\delta (t)$$ است.
• $$h(t-i.\Delta T)$$، پاسخ سیستم به ضربه واحد تاخیریافته $$\delta(t-i.\Delta T)$$ به اندازه $$i.\Delta T$$ است.
• $$A.h(t-i. \Delta  T)$$، پاسخ سیستم به ضربه‌ای با مساحت A است که به اندازه $$i.\Delta T$$ تاخیر یافته است.
• $$f(i.\Delta T)$$، ارتفاع تابع در زمان $$t=i.\Delta T$$ است.
• $$f(i.\Delta T).\Delta T$$، مساحت ضربه در $$t=i.\Delta T$$ است.
• پاسخ ضربه تاخیر یافته و جابه‌جا شده، با $$f(i.\Delta T).\Delta T. h(t-i. \Delta T)$$ نشان داده می‌شود.

بنابراین، پاسخ سیستم به مجموعه ضربه‌های تاخیر یافته را می‌توان با رابطه زیر نوشت:

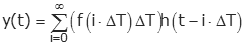
در معادله بالا، $$y(t)$$ خروجی، $$i.\Delta T$$ تاخیر زمانی هر ضربه و $$(f(i.\Delta T).\Delta T)$$ مساحت ضربه iاُم است.

اگر حد $$\Delta T \to0$$‌ را اعمال کنیم، مجموع به انتگرال کانولوشن (با $$i.\Delta T=\lambda$$ و $$\Delta T=d\lambda$$) تبدیل می‌شود:

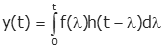
این دقیقاً همان قضیه کانولوشن است.

رابطه بالا را اغلب با حدود منفی و مثبت بی‌نهایت تعریف می‌کنند:

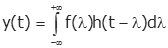
البته در مبحث مورد نظر ما، این دو انتگرال با هم برابر هستند، زیرا برای $$\lambda <0$$،  $$f(\lambda)=0$$ است.

آرگومان انتگرال را می‌توان به فرم زیر نوشت:

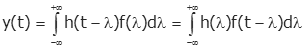
کانولوشن را با نماد ستاره (*) نشان می‌دهند:

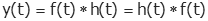
معادله اخیر بیان می‌کند که خروجی برابر با مجموع پاسخ‌ ضربه‌ها است.

هریک از پاسخ‌های ضربه به همراه مجموع آن‌ها در شکل زیر نشان داده شده است.

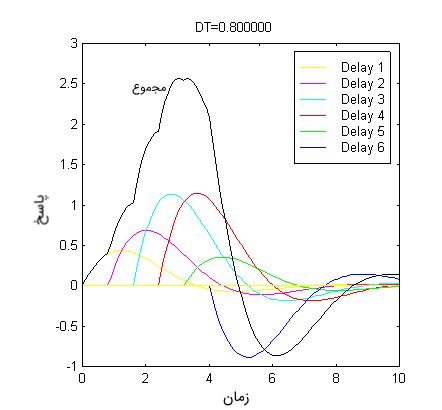
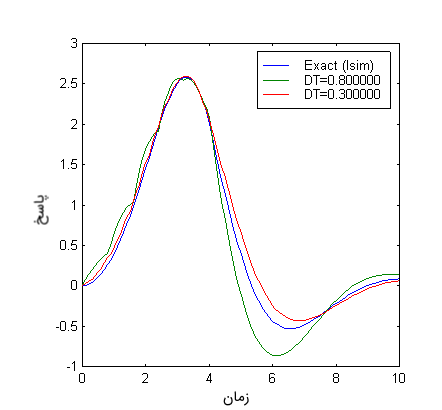
اگر $$\Delta T$$ کوچک‌تر شود، دقت تقریب بهبود پیدا می‌کند. برای مثال، اگر $$\Delta T=0.8$$ را به $$\Delta T=0.3$$ تبدیل کنیم، می‌بینیم که پاسخ تقریبی به پاسخ دقیق نزدیک‌تر می‌شود. شکل زیر این موضوع را نشان می‌دهد (نتایج با نرم‌افزار متلب رسم شده‌اند).

محاسبه کانولوشن با متلب

شکل زیر، مقایسه پاسخ «دقیق» و پاسخ محاسبه شده با تابع «conv» متلب را نشان می‌دهد.

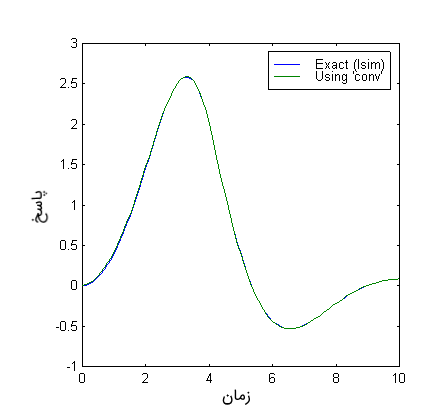
با نوشتن دستور «help conv» در متلب می‌توانید نحوه کار با این تابع را ببینید.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

برنامه متلب مربوط به شکل‌های بالا به شرح زیر است:

1DT=0.1;
2DT1=0.8;
3DT2=0.3;
4
5t=0:DT:10;		%Time (high resolution)
6f=(sin(t).*t+1).*(t<4.1);
7t1=0:DT1:10;	%Time (low resolution)
8f1=(sin(t1).*t1+1).*(t1<4.1);
9t2=0:DT2:10;	%Time (medium resolution)
10f2=(sin(t2).*t2+1).*(t2<4.1);
11
12sys=tf(1,[1 1 1]);
13
14plot(t,f,'b');
15xlabel('Time');
16ylabel('Input');
17title('Input vs Time');
18pause;
19
20hold on;
21bar(t1,f1,1,'c');
22ax=axis;		%Add axis
23plot([ax(1) ax(2)],[0 0],'k:')
24plot([0 0],[ax(3) ax(4)],'k:')
25axis(ax)
26bar(t1,f1,1,'c');
27title('Input vs Time and discrete approximation');
28plot(t,f,'b');
29hold off
30pause;
31
32plot(t,f,'b');
33xlabel('Time');
34ylabel('Input');
35
36hold on;
37stem(t1,f1,'g');
38title('Input vs Time and approximation with impulses');
39hold off
40pause;
41
42impulse(sys,t);
43title('Impulse response of system');
44xlabel('Time');
45ylabel('Output');
46pause
47
48h=impulse(sys,t);		%impulse response of system.
49colors='ymcrgb';
50
51imp=zeros(length(t),length(t1));
52for i=1:length(t1),
53   offset=(i-1)*round(DT1/DT);
54   x=h*f1(i)*DT1;
55   imp(offset+1:length(t),i)=x(1:length(t)-offset);
56   plot(t,imp(:,i),colors(mod(i-1,6)+1));
57   hold on;
58end
59ttl=sprintf('Scaled and Delayed Impulse Response DT=%f',DT1);
60title(ttl);
61xlabel('Time');
62ylabel('Response');
63legend('Delay 1','Delay 2','Delay 3','Delay 4','Delay 5','Delay 6')
64pause;
65approx=sum(imp,2);
66plot(t,approx,'k');
67gtext('Sum of impulses is shown in black');
68pause;
69hold off;
70
71imp2=zeros(length(t),length(t1));
72for i=1:length(t1),
73   offset=(i-1)*round(DT2/DT);
74   x=h*f2(i)*DT2;
75   imp2(offset+1 :length(t),i)=x(1:length(t)-offset,:);
76   plot(t,imp2(:,i),colors(mod(i-1,6)+1));
77   hold on;
78end
79hold off;
80ttl=sprintf('Scaled and Delayed Impulse Response DT=%f',DT2);
81title(ttl);
82xlabel('Time');
83ylabel('Response');
84pause;
85
86approx2=sum(imp2,2);
87soln=lsim(sys,f,t);
88plot(t,soln,t,approx,t,approx2);
89title('Sum of impulse responses');
90xlabel('Time');
91ylabel('Response');
92legend('Exact (lsim)',sprintf('DT=%f',DT1),sprintf('DT=%f',DT2));
93pause;
94
95soln2=conv(f,h)*DT;
96plot(t,soln,t,soln2(1:length(t)));
97title('Exact response, and using Matlab''s ''conv'' function');
98xlabel('Time');
99ylabel('Response');
100legend('Exact (lsim)','Using ''conv''');

بررسی شهودی انتگرال کانولوشن

برای بررسی شهودی انتگرال کانولوشن، تعریف کانولوشن یا معادل آن را در نظر بگیرید:

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

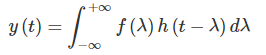
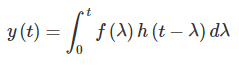
پاسخ ضربه سیستمی را که ابتدای این آموزش بررسی کردیم، مجدداً در نظر بگیرید:

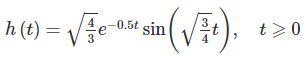
برای یافتن پاسخ $$y(t)$$ سیستم به ورودی $$f(t)$$ در $$t=1$$، باید انتگرال زیر را برای $$t=1$$‌ محاسبه کنیم:

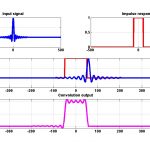
برای درک شهودی انتگرال کانولوشن، ضرب $$f(\lambda)h(t- \lambda)$$ را در نظر بگیرید. شکل $$f(\lambda)$$ که همان ورودی است. شکل $$h(t-\lambda)$$ نیز یک نسخه معکوس شده از پاسخ ضربه را با تاخیر زمانی t (در این مثال 1 ثانیه) نشان می‌دهد. این دو نمودار همراه با حاصل‌ضرب‌شان (خط سیاه ممتد) در شکل زیر نشان داده شده‌اند. تابع $$h(t-\lambda)$$، به رنگ ارغوانی رسم شده است.

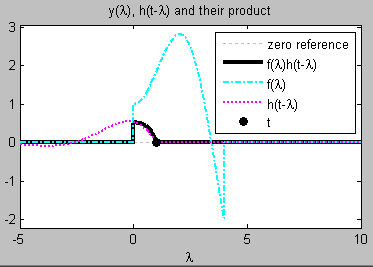
شکل زیر نتیجه انتگرال را برای کل محدوده زمانی نشان می‌دهد.

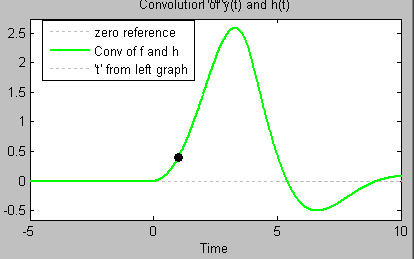
اگر t زیاد شود، تابع $$h(t-\lambda)$$ بیشتر به سمت راست جابه‌جا می‌شود. ضرب و انتگرال را می‌توان برای هر مقدار t به‌منظور به‌دست آوردن پاسخ $$y(t)$$ سیستم انجام داد. نمودارهای زیر، مشابه شکل‌های قبلی هستند، با این تفاوت که در آن‌ها $$t=4$$ است.

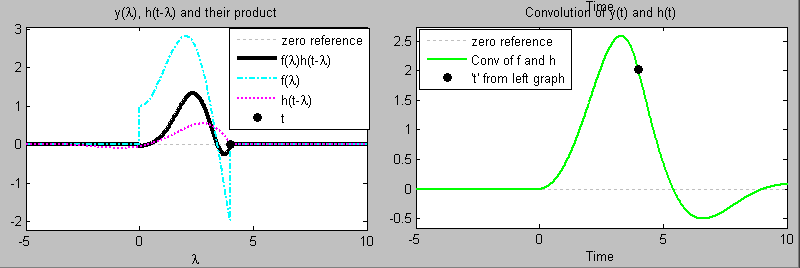
با استفاده از انتگرال کانولوشن، می‌توان خروجی هر سیستم خطی را با ورودی و پاسخ ضربه آن محاسبه کرد. هرچند، انتگرال‌گیری اغلب دشوار است و نمی‌توان آن را صریحاً محاسبه کرد.

کانولوشن از دیدگاه سیستم

یک سیستم خطی تغییرناپذیر با زمان (LTI) را در نظر بگیرید. ورودی سیستم $$x(t)$$ و خروجی آن، $$y(t)$$ است.

اگر به سیستم بالا، ورودی ضربه $$\delta$$ را اعمال کنیم، خروجی، پاسخ ضربه خواهد بود.

اگر ضربه ورودی، تاخیر داشته باشد، پاسخ نیز تاخیر خواهد داشت.

به دلیل خاصیت خطی سیستم، اگر ورودی را در هر عاملی ضرب کنیم، خروجی نیز در همان عامل ضرب خواهد شد. بنابراین، می‌توانیم ورودی و در نتیجه خروجی را در $$x(\lambda) d \lambda$$ ضرب کنیم.

اگر از ورودی انتگرال بگیریم، از خروجی نیز انتگرال گرفته می‌شود. در این حالت، حد بالای انتگرال را +t در نظر می‌گیریم. این مقدار می‌تواند $$+\infty$$‌ نیز باشد. همچنین، حد پایین را نیز می‌توانیم برابر $$-\infty$$ قرار دهیم.

با توجه به خاصیت جابه‌جایی تابع ضربه (اگر $$\lambda>0$$ و $$t.0$$)، داریم:

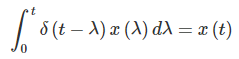
در نتیجه، با اعمال ورودی $$x(t)$$‌به سیستم، خروجی به‌صورت زیر خواهد بود:

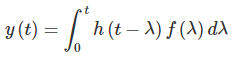
مثال

می‌خواهیم حل دقیق انتگرال کانولوشن سیستمی با پاسخ ضربه و ورودی زیر را محاسبه کنیم:

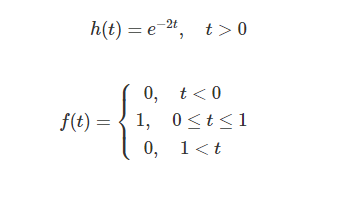
خروجی با رابطه انتگرال کانولوشن زیر به‌دست می‌آید:

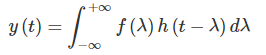
از آن‌جایی که تابع ورودی، سه ناحیه مجزا دارد، باید انتگرال را به سه بخش جدا تقسیم کنیم.

بازه اول: $$t<0$$

برای $$t<0$$‌، آرگومان $$(t-\lambda)$$ تابع ضربه همواره منفی است. از آن‌جایی که در این حالت، $$h(t-\lambda)=0$$، نتیجه انتگرال صفر است. این وضعیت، در شکل زیر نشان داده شده است ($$t=-0.2$$).

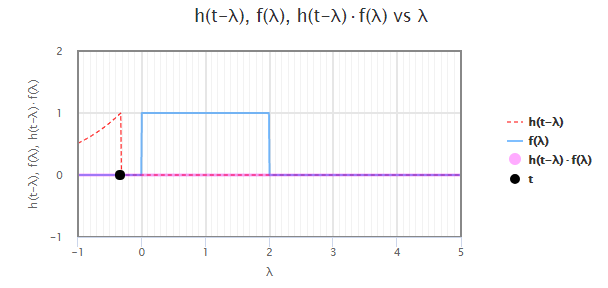
بنابراین، نتیجه انتگرال بازه اول به‌صورت زیر خواهد بود:

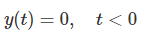
بازه دوم: $$0$$

در بازه $$0$$، باید انتگرال را فقط از $$\lambda =0$$ تا $$\lambda =t$$ حساب کنیم. شکل زیر، این وضعیت را نشان می‌دهد.

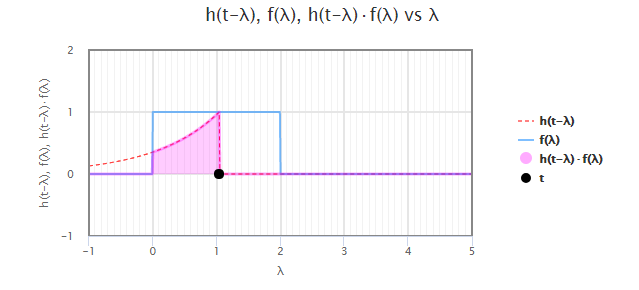
اکنون می‌توانیم خروجی را محاسبه کنیم:

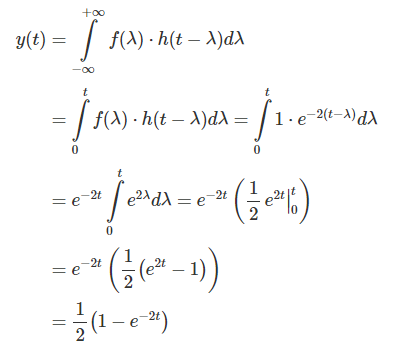
خروجی در این بازه به‌صورت زیر به‌دست می‌آید:

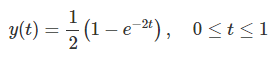
بازه سوم: $$t>1$$

در این بازه، باید انتگرال را از $$\lambda =0$$ تا $$\lambda =1$$ محاسبه کنیم، زیرا وقتی $$\lambda <0$$ و $$\lambda>1$$ باشد، $$f(\lambda)=0$$ است:

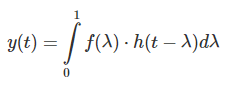
این وضعیت در شکل زیر نشان داده شده است ($$t=1.2$$).

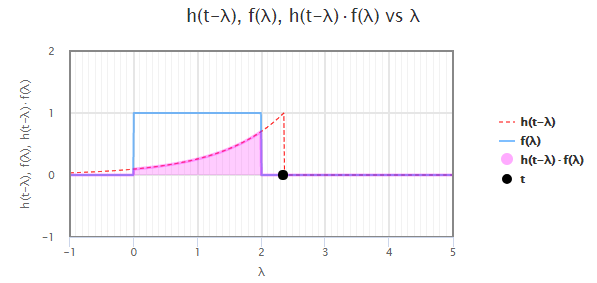
خروجی در این حالت، به‌صورت زیر محاسبه می‌شود:

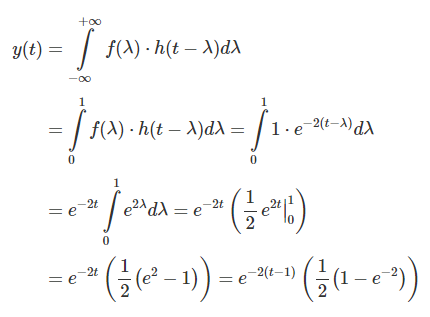
در نتیجه:

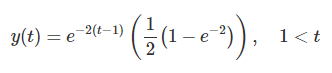
در نهایت، پاسخ سیستم به ورودی، خروجی زیر خواهد بود:

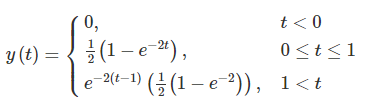
شکل خروجی نهایی، به‌صورت زیر است:

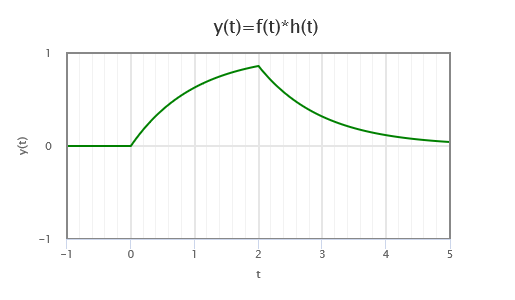
محاسبه کانولوشن با تبدیل لاپلاس

برای شرح استفاده از تبدیل لاپلاس در محاسبه کانولوشن، از یک مثال استفاده می‌کنیم. فرض کنید پاسخ ضربه یک سیستم، به‌صورت زیر باشد:

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

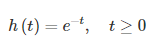
می‌خواهیم خروجی را به‌ازای ورودی زیر محاسبه کنیم:

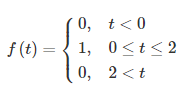
می‌دانیم خروجی با رابطه کانولوشن $$y(t)=f(t)*h(t)$$ محاسبه می‌شود. ویژگی کانولوشن تبدیل لاپلاس به‌صورت زیر است:

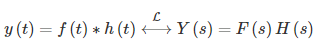
بنابراین، باید $$f(t)$$ و $$h(t)$$ را با کمک جدول محاسبه تبدیل لاپلاس به‌دست آوریم که نتیجه آن به‌شکل زیر است:

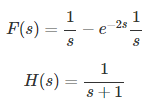
بنابراین:

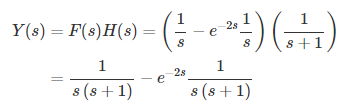
با استفاده از فرمول‌های تبدیل لاپلاس معکوس، داریم:

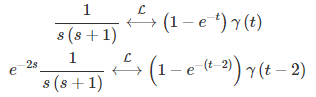
اکنون می‌توانیم $$y(t)$$ را محاسبه کنیم:

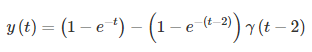
در عبارات بالا $$\gamma (t)$$ همان پله واحد است.

اگر مطالب بیان شده برای شما مفید بوده و علاقه‌مند به یادگیری مباحث مرتبط با آن هستید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• مجموعه آموزش‌های مهندسی برق
• مجموعه آموزش های پردازش تصویر و پردازش سیگنال
• مجموعه آموزش‌های مهندسی کنترل
• تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس

^^