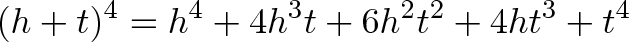درک ترکیب در ریاضی با استفاده از مفهوم ضرب – به زبان ساده

در این نوشته یکی دیگر از کارکردهای عمل ضرب یعنی ترکیب فهرست‌بندی‌ها را بررسی می‌کنیم.

ضرب یک عمل ریاضی ساده و جالب محسوب می‌شود. بسته به این که در چه زمینه‌ای از این عمل استفاده می‌کنید، معنی این عمل ریاضی می‌تواند متفاوت باشد:

• افزایش مقیاس یا بزرگ‌تر کردن یک عدد
• چرخش یک بردار بدون نیاز به سینوس یا کسینوس

تغییر زاویه نگاه به عمل ضرب چند کاربرد دارد:

از بخش‌های دیگر ریاضی نیز رمزگشایی می‌کند. درک قضیه دوجمله‌ای، جبر بولی (که در مدارهای رایانه کاربرد دارد)، و حتی بخش‌هایی از حسابان با داشتن چنین تفسیری از «ضرب» آسان‌تر خواهد بود.

ذهن ما روشن‌تر می‌شود. ریاضیات مدل‌هایی در اختیار ما قرار می‌دهد و خوب است که ببینیم یک مدل چطور می‌تواند کاربردهای مختلفی داشته باشد. زمانی که ماهیت واقعی یک چکش را شناخته باشید، حتی از یک آچار می‌توانید برای کوبیدن میخ استفاده کنید.

روش ضرب چندرقمی که در دوران دبستان آموخته‌ایم کاملاً مفید است. برای مثال به وسیله آن می‌توانیم احتمال‌های مختلف برای پرتاب چندباره سکه را محاسبه کنیم.

ما همیشه مشغول استفاده از ترکیب هستیم.

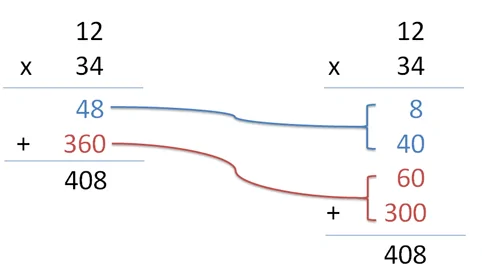
حاصلضرب 34 × 12 را چطور می‌توان یافت؟ بدین منظور باید محاسبه زیر را روی کاغذ بنویسیم:

روش محاسبه این چنین است که 4 ضرب در 12 برابر با 48 است. 3 ضرب در 12 برابر با 36 است، که البته آن را یک رقم جا به جا می‌کنیم و بنابراین 360 است. بعد 48 را با 360 جمع می‌کنیم و نتیجه برابر با 408 خواهد بود.

برخی به روش فوق عمل می‌کنند. اما بعضی افراد دیگر ضرب‌های دو رقمی را نیز تجزیه می‌کنند و در واقع به روش زیر ضرب می‌کنند:

در تصویر فوق چه اتفاقی افتاده است؟ 12 × 4 در واقع همان (2+ 10) × 4 است که نتیجه 8+ 40 خواهد بود. می‌توان گام نخست (به رنگ آبی) را به صورت دو ضرب مجزا در نظر گرفت یعنی 10 × 4 و 2 × 4.

ما چنان به ترکیب کردن و اجرای محاسبات عادت کرده‌ایم که این مراحل را در هم ادغام می‌کنیم؛ اما در واقع این مراحل وجود دارند. برای مثال:

4 × 17

= 4 × (10 + 7)

= 40 + 28

= 68

اما معمولاً آن را به این صورت تجزیه نمی‌کنیم.

به طور مشابه گام قرمز رنگ یعنی 12 × 3 نیز در واقع 12 × 30 است چون 3 در ستون دهگان است. بنابراین داریم:

30 × (10 + 2)

300 + 60

در این مورد نیز عدد را به دو بخش افراز کردیم. شاید از خود بپرسید که این‌ها چه ربطی به ترکیب دارد. در ادامه پاسخ این سؤال را خواهید یافت.

تکنیک FOIL

در این بخش نگاهی دقیق‌تر به فرایند محاسبات فوق خواهیم داشت. 34 × 12 در واقع به صورت زیر است:

(10 + 2) × (30 + 4)

= 300 + 40 + 60 + 8

این تجزیه مانند معادله جبری (a + b) * (c + d) است.

در واقع اتفاق مشابهی افتاده است. در هر مورد ما مشغول ضرب یک گروه در گروه دیگر هستیم. ما می‌توانیم هر آیتم از گروه قرمز (10 و 2) را برداریم و با عناصر گروه آبی (30 و 4) ترکیب کنیم. ما عناصر گروه قرمز را با هم مخلوط نمی‌کنیم. عناصر آبی را نیز با هم دیگر مخلوط نمی‌کنیم.

این تکنیک ترکیب غالباً FOIL یعنی «ابتدا-داخل-خارج-انتها» (first-inside-outside-last) نامیده می‌شود و در واقع مایه سردرد دانش آموزان است؛ اما این یک عملیات عجیب و غریب نیست. کافی است همه چیز را روی یک جدول قرار دهید. ما در ضرب‌های خودمان همیشه از FOIL استفاده می‌کنیم.

زمانی که مشغول ضرب چندرقمی هستید، می‌دانید که نباید موارد هم گروه را ضرب کنید. بنابراین برای مثال ضرب 2 × 1 درست نیست، چون آن‌ها در یک ردیف هستند. به طور مشابه ضرب a در b نیز صحیح نیست چون در یک پرانتز هستند. ما تنها عناصر بالا و پایین را درهم ضرب می‌کنیم. یعنی یک آیتم باید از بالا و یک آیتم از پایین باشد.

ضرب‌های روزمره یعنی روش FOIL ایده‌ای در مورد درک ترکیب دو گروه به ما می‌دهند، چون هر بار یک عنصر از گروه A یا یک عنصر از گروه B ترکیب می‌شود. می‌بینید که گاهی اوقات خوب است همه احتمال‌ها را به صورت یک معادله بنویسیم.

بررسی یک مثال

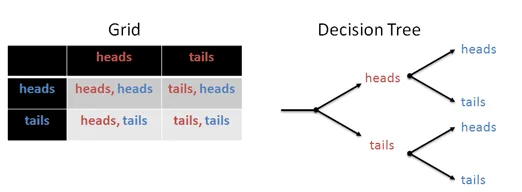
در این بخش مثالی را برای درک بهتر مسئله بررسی می‌کنیم. فرض کنید می‌خواهید همه ترکیب‌های ممکن پرتاب دو بار سکه را بیابید. روش‌های مختلفی برای این کار وجود دارد، مانند استفاده از یک جدول یا درخت تصمیم:

این روش‌ها هم خوب هستند؛ اما می‌خواهیم روش متفاوتی را دنبال کنیم. می‌توانیم این سؤال را با استفاده از قواعد زیر به یک معادله تبدیل کنیم:

جمع(OR) - ما می‌توانیم شیر (h) یا خط (t) بیاوریم: h + t

ضرب (AND) - ما ابتدا یک پرتاب «و» در ادامه پرتاب دوم را داریم: (h+t) * (h+t)

اما روش کار چگونه است؟

در واقع در این روش ترکیب را همان‌طور که معادله دوجمله‌ای را تجزیه می‌کردیم، تجزیه خواهیم کرد:

(a+b) * (c+d) = ac + bc + ad + bd

اگر به دقت نگاه کنید این قالب به این معنی است که باید یک a یا b انتخاب کرد و آن را با یکی از c یا d ترکیب کرد.

زمانی که یک جمع (a+b) را می‌بینیم می‌دانیم که باید یک متغیر را انتخاب کنیم: این «یا» آن. وقتی ضرب را می‌بینیم (گروه 1 × گروه 2) می‌دانیم که باید یک آیتم را از یک گروه در آیتم گروه دیگر ضرب کنیم: این «و» آن.

این میانبر یعنی AND برای ضرب و «OR» برای جمع یک روش متفاوت برای توصیف رابطه درون این معادله محسوب می‌شود. البته باید دقت کنید که وقتی می‌گوییم «سیصد و چهار» اغلب افراد فکر می‌کنند که منظور 304 است که آن نیز درست است. اما در این جا ما از قالب معادله‌ای خودمان استفاده کرده‌ایم.

بنابراین با همه این تفاصیل جمله «شیر یا خط» و «شیر یا خط» را می‌توانیم به صورت زیر بنویسیم:

همانند روش ضرب دوجمله‌ای می‌توانیم آن را به صورت زیر بسط دهیم:

نتیجه h² + 2ht + t² مانند روش جدول یا درخت تصمیم، همه حالت‌های ممکن را به ما نشان می‌دهد. همچنین اندازه (ضریب) هر ترکیب تعداد روش‌های ممکن برای رخداد را نشان می‌دهد:

• h² : یک راه برای داشتن دو شیر هست (h² یعنی hh یعنی شیر و شیر)
• 2ht: دو راه برای داشتن یک شیر و یک خط هست (ht یا th)
• t² : دو راه برای داشتن دو خط وجود دارد (tt).

فیلم آموزش المپیاد ریاضی مبحث ترکیبیات – مرحله اول + نکات و حل نمونه سوالات در فرادرس

کلیک کنید

مجموع ضرایب به صورت 1 + 2 + 1 = 4 است که کل حالت‌های ممکن را نشان می‌دهد. احتمال داشتن دقیقاً یک شیر و یک خط به صورت 2/4 یا به عبارت دیگر 50% است. ما این نتیجه را بدون استفاده از درخت یا جدول به دست آوردیم و راهنمای ما صرفاً عمل ضرب بوده است. یعنی دیگر به جدول یا درخت نیاز نداریم، چون می‌توانیم به صورت ذهنی محاسبه کنیم.

محاسبات ذهنی

اینک مثال خود را کمی بسط می‌دهیم. به چند روش مختلف می‌توان دقیقاً دو شیر و دو خط را در چهار بار پرتاب به دست آورد؟ شانس داشتن 3 شیر یا بیشتر چقدر است؟

اینک جمله ما به صورت زیر در آمده است:

(h OR t) AND (h OR t) AND (h OR t) AND (h OR t)

اگر به نتیجه نگاه کنیم، می‌بینیم که 6 روش برای داشتن 2 شیر و 2 خط وجود دارد. در واقع داریم 1 + 4 + 6 + 4 + 1 = 16 حالت. بنابراین تنها 6/16 یا به عبارت دیگر 37.5% شانس رخداد حالت متقارن (یعنی شیر و خط برابر) پس از چهار بار پرتاب وجود دارد. البته شاید کمی شگفت‌زده شوید، چون احتمال به دست آوردن حالت‌های غیرمتقارن بیشتر از حالت‌های متقارن است.

سؤال بعدی این بود که احتمال به دست آمدن 3 شیر یا بیشتر چقدر است؟ پاسخ این است که باید حالت‌های h³ یا h⁴ را بشماریم یعنی 4+1 = 5. بنابراین احتمال برابر 5/16 یا به عبارت دیگر 31.25% است که 3 شیر یا بیشتر داشته باشید.

برخی اوقات معادلات بهتر از جدول و درخت هستند. در بخش فوق دیدیم که چه میزان از اطلاعات را می‌توانیم تنها در یک خط ارائه کنیم. البته زمانی که یک ماشین حساب یا رایانه در دست داشته باشید، چنین فرمول‌هایی ارزش دو چندان خواهند داشت. اما مهم‌ترین دستاورد رویکرد فوق این است که ما یک ابزار دیگر به دست آورده‌ایم. بدین ترتیب می‌توانیم حالت‌های مختلف را به صورت معادله بنویسیم و از ضرب برای یافتن ترکیب استفاده کنیم.

جمع‌بندی

چند حوزه ریاضیاتی وجود دارند که می‌توان از این رویکرد ضربی در آن استفاده کرد:

• قضیه دوجمله‌ای – این قضیه با ظاهر ترسناک (h+t)^n را به ضرایبش ربط می‌دهد. اگر زیرک باشید درمی‌یابید که می‌توانید از ترکیب و جایگشت برای یافتن توان‌ها به جای ضرب کردن کل معادله استفاده کنید. این همان کاری است که قضیه دوجمله‌ای انجام می‌دهد. این قضیه جای صحبت بسیار دارد و در موارد مختلف از جمله مطالب مربوط به حسابان در آینده بیشتر در مورد آن توضیح خواهیم داد.
• جبر بولی – علاقه‌مندان رایانه عاشق تبدیل شروطی مانند OR یا AND به جمله‌های ریاضیاتی هستند. این نوع از منطق AND/OR در زمان طراحی مدارهای رایانه مورد استفاده قرار می‌گیرد و حالت‌های مختلف با استفاده از معادلات (و نه نمودارها) بیان می‌شوند که رویکرد مفیدی است. نام جذاب این تکنیک جبر بولی است که در ادامه مطالب ریاضیات به زبان ساده در بلاگ فرادرس به آن نیز خواهیم پرداخت.
• حسابان – حسابان از این تفسیر ضربی ما بهره‌های بسیار بیشتری می‌برد. در ابتدا باید اشاره کرد که قضیه دوجمله‌ای باعث شده است کار کردن با معادلاتی مانند x^2 بسیار آسان‌تر باشد. دوم این که یک تفسیر از حسابان همان بسط عمل ضرب است. امروزه ما به این تفکر که ضرب چیزی بیشتر از تکرار عمل جمع است عادت کرده‌ایم.
• ترکیب‌های پیچیده‌تر – فرض کنید 3 میهمان به نام‌های علی، داوود و مرضیه دارید و آن‌ها با خود نوشابه، بستنی یا ماست می‌آورند. اگر کسی زنگ در را بزند حالت‌های مختلف برای این که هر یک چه آورده باشد چیست؟ همه پاسخ‌ها در معادله (علی + داوود + مرضیه) * (نوشابه + بستنی + ماست) است.

سخن پایانی

در این مقاله دیدیم که می‌توان از مفهومی قدیمی به نام ضرب ایده‌های تازه‌ای گرفت. همیشه روش‌های متفاوت برای اندیشیدن وجود دارند. البته رویکردهای نو همیشه و همه جا هستند، فقط کافی است اندکی با ذهن باز با آن‌ها مواجه شویم تا بتوانیم آن‌ها را ببینیم. چه کسی فکر می‌کرد 12 × 34 مبنایی برای ترکیب باشد؟ اما دیدیم که عمل ضرب معمولی می‌تواند روشی برای محاسبه ترکیب‌های پیچیده باشد.

اگر این نوشته مورد توجه‌تان قرار گرفته، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های ریاضیات
• جایگشت و ترکیب — به زبان ساده
• ضرب داخلی بردارها — به زبان ساده
• مجموعه آموزش های آمار، احتمالات و داده‌کاوی
• آموزش ترکیب، تساوی و اعمال جبری روی توابع در ریاضی پایه
• یادگیری ترکیب و جایگشت به همراه مثال های عینی — به زبان ساده
• ضرب خارجی بردارها — به زبان ساده

==