ضرب دکارتی مجموعه ها و مختصات دکارتی — به زبان ساده

در نظریه مجموعه‌ها، ضرب دکارتی از اهمیت خاصی برخوردار است. زیرا مفاهیم دیگر مثل رابطه و تابع براساس آن بنا نهاده شده‌اند. البته به عنوان تعمیم ضرب دکارتی دو مجموعه، می‌توان از ضرب دکارتی n مجموعه نیز صحبت کرد. مطالعات «رنه دکارت» (Rene Descartes) فیلسوف و دانشمند بزرگ فرانسوی در زمینه مجموعه‌ها در قرن ۱۵ میلادی،‌ موجب به وجود آمدن مفهوم جدیدی در ریاضیات به نام ضرب مجموعه‌‌ها گردید. به همین دلیل این مفهوم به نام ضرب دکارتی یا ضرب کارتزین معرف است. البته بعدها این مفهوم گسترش پیدا کرد و در هندسه تحلیلی به کار رفت.

برای مطالعه بهتر این نوشتار پیشنهاد می‌شود، مطلب مجموعه ها در ریاضیات – مفاهیم پایه و همچنین اجتماع، اشتراک و تفاضل مجموعه ها — به زبان ساده را مطالعه کنید.

ضرب دکارتی دو مجموعه

همانطور که می‌دانید، هر مجموعه بوسیله اعضای آن مشخص می‌شود. تشخیص اینکه آیا شئ درون مجموعه قرار دارد یا خیر به عهده قانون عضویت مجموعه است. بنابراین برای تعیین یک مجموعه یا باید اعضای آن را یک به یک معرفی کنیم یا قانون عضویت را برای آن بنویسیم.

فیلم آموزش مبانی آنالیز ریاضی – مرور، حل مثال و تست کنکور ارشد – بخش یکم در فرادرس

کلیک کنید

برای اینکه ضرب دکارتی دو مجموعه را بهتر بشناسیم، ابتدا به معرفی «زوج مرتب» (Ordered Pair) پرداخته سپس از آن برای معرفی ضرب دو مجموعه کمک می‌گیریم.

زوج مرتب

اگر x و y دو شئ باشند، زوج مرتب x و y را به صورت $$(x,y)$$ نشان می‌دهند. در این حالت، عنصر اول یعنی x را مولفه اول و عنصر دوم یعنی y را مولفه دوم می‌نامند. در زوج مرتب، ترتیب قرار گیری عناصر در مولفه‌ها مهم است.

نکته: جابجایی مولفه‌ها، باعث ایجاد زوج مرتب جدید می‌شود. به این ترتیب برای دو زوج مرتب $$(x,y)$$ و $$(y,x)$$ لزوما تساوی برقرار نیست. در نتیجه خواهیم داشت:

$$\large (x,y)\neq (y,x)$$

ضرب دوکارتی دو مجموعه A و B

ضرب دکارتی دو مجموعه نیز خود یک مجموعه است که بوسیله قانون عضویت، تعریف می‌شود. فرض کنید A و B دو مجموعه باشند، آنگاه ضرب دکارتی یا «ضرب کارتزین» (Cartesian Product) این دو مجموعه، توسط مجموعه زیر مشخص می‌شود:

$$\large \displaystyle A\times B=\{\,(a,b)\mid a\in A\ {\mbox{ and }}\ b\in B\,\}$$

مشخص است که اعضای این مجموعه به صورت زوج مرتب‌هایی هستند که مولفه اول از مجموعه اول و مولفه دوم از مجموعه دوم انتخاب می‌شود.

برای مثال فرض کنید که مجموعه A به صورت $$A=\{x,y,z\}$$ و مجموعه B نیز به صورت $$B=\{1,2,3\}$$ تعریف شده باشند. منظور از $$A\times B$$ مجموعه‌ای به صورت زیر است.

$$\large A\times B =\{(x,1),(x,2),(x,3),(y,1),(y,2),(y,3),(z,1),(z,2),(z,3)\}$$

البته ارتباط بین اعضای این مجموعه و مجموعه‌های A و B را می‌توان به صورت جدول زیر نیز نشان داد.

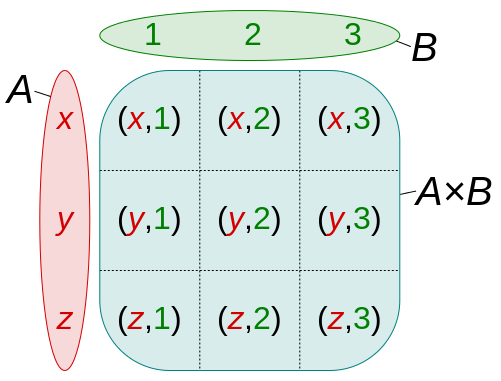
اگر ضرب دکارتی دو مجموعه B و A را بنویسیم خواهیم دید که ضرب دکارتی خاصیت جابجایی ندارد. یعنی $$A\times B \neq B\times A$$.

$$\large A\times B =\{(x,1),(x,2),(x,3),(y,1),(y,2),(y,3),(z,1),(z,2),(z,3)\}$$

$$\large B\times A =\{(1,x),(2,x),(3,x),(1,y),(2,y),(3,y),(1,z),(2,z),(3,z)\}$$

$$\large A\times B \neq B\times A$$

در این حالت مشخص است که اگر مجموعه A دارای $$n_A$$ عضو و مجموعه B نیز دارای $$n_B$$ عضو باشد، مجموعه $$A\times B$$ نیز دارای $$n_A\times n_B$$ عضو خواهد بود. اگر ضرب دکارتی را براساس جدول بالا در نظر بگیریم، تعداد اعضای حاصل از ضرب دکارتی دو مجموعه، بوسیله حاصلضرب سطرها و ستون‌های جدول مشخص می‌شود.

به عنوان یک مثال دیگر، فرض کنید مجموعه اعداد حقیقی که آن را با ℝ نشان می‌دهیم را در خودش ضرب دکارتی کنیم. به این ترتیب خواهیم داشت:

$$\large ℝ×ℝ=\{(x,y)| x , y \in ℝ \}$$

این مجموعه از زوج‌های مرتب را فضای دکارتی حاصل از اعداد حقیقی گویند. برای نمایش این زوج‌ها از مختصاتی استفاده می‌کنند که به مختصات دکارتی معروف است.

تعمیم ضرب دکارتی در چند بعد

به عنوان یک تعمیم برای ضرب دکارتی دو مجموعه، می‌توان از ۳ مجموعه یا بیشتر استفاده کرد. اگر A، ‌B، C سه مجموعه باشند، منظور از ضرب دکارتی آن‌ها ایجاد «سه‌تایی‌های مرتب» (Triples) است. در ادامه نمایش و اعضای ضرب دکارتی برای سه مجموعه نشان داده شده است.

$$\large A\times B \times C =\{(x,y,z)|x \in A , y\in B, z\in C\}$$

همینطور، منظور از ضرب دکارتی n مجموعه $$A_1,A_2,\cdots ,A_n$$، یک «nتایی مرتب» (Tuples) است که به صورت زیر تعریف می‌شود.

$$\large A_1\times A_2 \times \cdots \times A_n =\{(x_1,x_2,\cdots, x_n)|x_1 \in A_1 , x_2\in A_2,\cdots ,x_n\in A_n\}$$

مختصات دکارتی

یک خط مستقیم را در نظر بگیرید. اگر برای این خط، جهتی در نظر بگیریم، می‌توان آن‌ را یک «محور» (Axis) نامید. از محور برای نمایش اعداد استفاده می‌کنند زیرا برای اعداد، ترتیب وجود دارد و می‌توان به واسطه این ترتیب، جهت بزرگتر یا کوچکتر شدن را روی محور در نظر گرفت.

فیلم آموزش ساختمان گسسته با رویکرد حل مساله در فرادرس

کلیک کنید

در زیر یک محور برای نمایش اعداد حقیقی دیده می‌شود.

حال یک صفحه را در نظر بگیرید که از دو محور عمود بر هم ساخته شده که هر محور نیز شامل اعداد حقیقی است. نقاط این صفحه را می‌توان به صورت زوج‌های مرتبی نشان داد که از ضرب دکارتی اعداد حقیقی حاصل می‌شوند. چنین فضای دوبعدی را مختصات دکارتی یا کارتزین می‌نامند و با $$R^2$$ نشان می‌دهند.

ویژگی‌های مختصات دکارتی

با توجه به ساختار مختصات دکارتی، در ادامه به بررسی چند ویژگی آن می‌پردازیم:

• هر دو محور در این مختصات بر یکدیگر عمودند.
• هر دو محور با مقیاس واحد مدرج شده‌اند. به این معنی که طول واحد برای هر دو محور منظور شده است. منظور از طول واحد، فاصله‌ی دو نقطه از محور است که با مقدار ۱ برابر است.
• هر نقطه در مختصات دکارتی با یک زوج مرتب به صورت $$(x,y)$$ نشان داده می‌شود. x را طول و y را عرض نقطه می‌نامند.
• نقطه برخورد دو محور دارای مختصات $$(0,0)$$ است. به این معنی که طول و عرض آن برابر با صفر است. به این نقطه «مبدا مختصات» (Origin) می‌گویند که معمولا با حرف O نشان داده می‌شود.
• اگر مختصات دکارتی را برای فضای اعداد حقیقی به کار ببریم، به آن فضای دو بعدی ($$R^2$$) از اعداد حقیقی می‌گوییم.
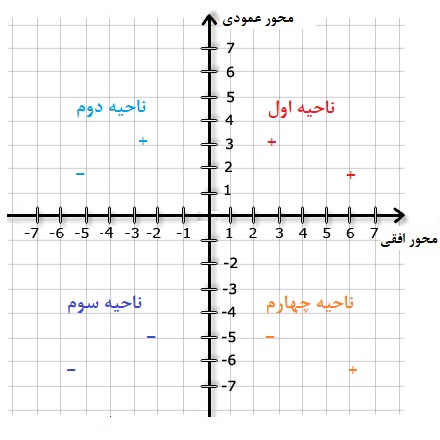
• نواحی چهارگانه روی مختصات دکارتی وجود دارد که وضعیت منفی یا مثبت بودن طول یا عرض نقطه را نشان می‌دهد. در تصویر زیر، این قسمت‌ها روی مختصات دکارتی مشخص شده‌اند. واضح است که ناحیه اول قسمتی است که طول و عرض نقطه‌ها در آن مثبت هستند. در ناحیه دوم، طول‌ها منفی و عرض‌ها، مثبت و در ناحیه سوم، هم طول و هم عرض نقطه‌ها، منفی است. در ناحیه چهار نیز برعکس ناحیه دوم، طول‌ها مثبت و عرض‌ها منفی است.

• ممکن است مقیاس محور افقی یا عمودی برحسب لگاریتم اعداد حقیقی محاسبه شود. در این حالت مختصات را مختصات دکارتی لگاریتمی روی محور x یا y می‌نامند. در تصویر زیر، محور افقی مختصات دکارتی، براساس لگاریتم مبنای ۱۰ تعیین شده است.

فضای سه و چند بعدی

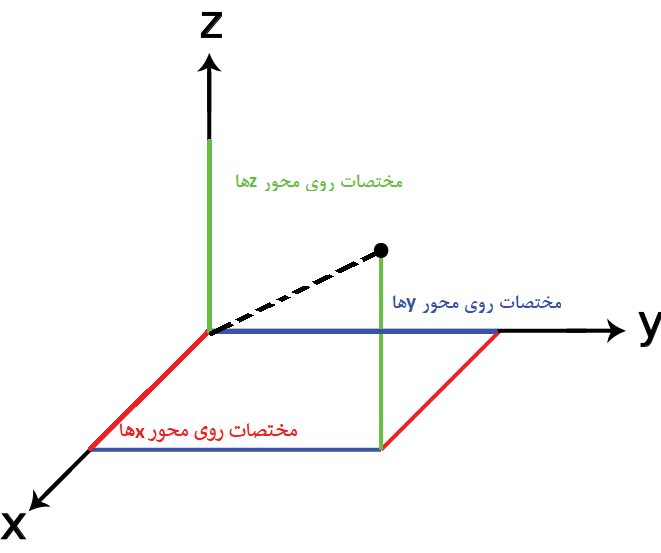
فرض کنید که مختصات دکارتی براساس $$R\times R\times R$$ ساخته شده باشد. مختصات حاصل از این ضرب به صورت سه محور عمود بر هم در فضای سه بعدی نمایش داده می‌شود که به مختصات دکارتی در سه بعد شهرت دارد. در زیر نمایش مختصات دکارتی سه بعدی را می‌بینید که توسط ضرب دکارتی $$R\times R\times R=R^3$$ حاصل می‌شود. با این مختصات می‌توان نقاطی با سه مولفه را نمایش داد. به این ترتیب مختصات یک نقطه در فضای سه بعدی برای مثال به صورت $$A(1,2,3)$$ خواهد بود که اولین مولفه را طول، دومین مولفه را عرض و سومین مولفه را ارتفاع می‌نامند.

به همین ترتیب مختصات nبعدی نیز به کمک ضرب دکارتی n مجموعه ساخته می‌شود. اگر این مجموعه‌ها، مجموعه اعداد حقیقی باشند، فضای حاصل را به صورت $$R^n$$ نشان می دهند. به این ترتیب هر نقطه با n مولفه مشخص می‌شود.

در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضیات، آموز‌ش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• مجموعه‌ آموزش‌های ریاضی و فیزیک
• مجموعه‌ آموزش‌های دبیرستان و پیش‌دانشگاهی
• معادله صفحه — به زبان ساده
• معادله خط — به زبان ساده
• چندجمله‌ای‌ها – به زبان ساده
• رسم نامعادلات و نامساوی‌ های خطی — به زبان ساده
• معادله های پارامتری — به زبان ساده

^^