گراف دو همبند (Biconnected Graph) – از صفر تا صد

در این مطلب، مفهوم گراف دو همبند و مولفه دو همبند مورد بررسی قرار می‌گیرد و روش تشخیص هر یک از آن‌ها بیان می‌شود. همچنین، پیاده‌سازی روش‌های بیان شده در زبان‌های برنامه‌نویسی گوناگون شامل «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java)، «پایتون ۳» (Python 3) انجام خواهد شد.

یک گراف بدون جهت، «دو همبند» (Biconnected Graph) نامیده می‌شود اگر بین هر دو «راس» (Node) آن، حداقل دو مسیر مجزا وجود داشته باشد. در یک گراف دو همبند، چرخه ساده‌ای بین هر دو راس وجود دارد. بر اساس قرارداد، دو گره متصل شده به وسیله یک یال، یک گراف دو همبند می‌سازند؛ اما این مورد، خصوصیت بیان شده در خط پیشین را تایید نمی‌کند. برای یک گراف با بیش از دو راس، خصوصیت بالا باید وجود داشته باشد تا گراف دو همبند محسوب شود. مثال‌هایی از گراف دو همبند و غیر دو همبند در ادامه آمده است.

روش بررسی دو همبند بودن یک گراف

یک گراف دو همبند است اگر همبند باشد و هیچ «راس برشی» (ٰArticulation Point) نداشته باشد. بنابراین، برای تشخیص گراف دو همبند، نیاز به تشخیص دو چیز در یک گراف است:

1. گراف هم‌بند باشد.
2. هیچ راس برشی در گراف وجود نداشته باشد.

کار را می‌توان از هر راسی آغاز کرد و «پیمایش جستجوی اول عمق» (Depth-First Search Traversal | DFS) را انجام داد. در پیمایش DFS، بررسی می‌شود که آیا راس برشی وجود دارد یا خیر. اگر هیچ راس برشی پیدا نشد، گراف دو همبند است. در نهایت، باید بررسی شود که آیا همه راس‌ها از پیمایش جستجوی اول عمق در دسترس هستند یا خیر. اگر همه راس‌ها در دسترس نباشند بدین معنا است که گراف حتی متصل نیز نیست. در ادامه، پیاده‌سازی رویکرد بیان شده در زبان‌های برنامه‌نویسی گوناگون ارائه شده است.

برنامه تشخیص گراف دو همبند در ++C

برنامه تشخیص گراف دو همبند در جاوا

برنامه تشخیص گراف دو همبند در پایتون

خروجی قطعه کدهای بالا، به صورت زیر است.

Yes
Yes
No
No
Yes

تابع بالا، یک DFS ساده با آرایه‌های اضافی است. بنابراین، پیچیدگی زمانی آن مشابه با DFS و برای ارائه لیست همجواری گراف، برابر با O(V+E)‎ است.

برنامه تشخیص مولفه دو همبند (Biconnected Components)

یک «مولفه دو همبند» (Biconnected Components) یک زیر گراف حداکثر دو همبند است. در این مطلب، روش نوشتن برنامه تشخیص مولفه دو همبند در گراف با استفاده از الگوریتم ارائه شده توسط «جان هاپکرافت» (John Hopcroft) و «رابرت تارجان» (Robert Tarjan) آموزش داده شده است.

فیلم آموزش نظریه گراف و کاربردها در فرادرس

کلیک کنید

همچنین، پیاده‌سازی روش ارائه شده، در زبان‌های «سی‌پلاس‌پلاس» (++C)، «جاوا» (Java) و «پایتون ۳» (Python 3) انجام شده است.

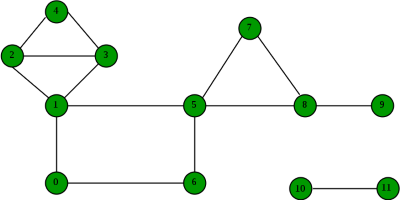
در گراف بالا، مولفه‌های دو همبند به شرح زیر هستند:

4–2 3–4 3–1 2–3 1–2‎‎‎‎

8–9

8–5 7–8 5–7

6–0 5–6 1–5 0–1

10–11

الگوریتم ارائه شده برای تشخیص مولفه دو همبند، بر پایه Disc و Low Value‌های موجود در قطعه کدهای مربوط به گراف دو همبند است. هدف، ذخیره‌سازی یال‌های ملاقات شده در پشته در حالی است که جستجوی اول عمق (Depth First Search) روی گراف انجام و به دنبال «راس‌های برشی» (Articulation Point) گشته می‌شود.

فیلم آموزش مقدمه ای بر هوش مصنوعی و عامل های هوشمند (رایگان) در فرادرس

کلیک کنید

به محض اینکه راس برشی پیدا شود، همه راس‌های ملاقات شده در طول DFS از نود u به بعد یک مولفه دو همبند را تشکیل می‌دهند. هنگامی که DFS برای یک مولفه همبند انجام شد، همه راس‌های ارائه شده در پشته یک مولفه دو همبند را تشکیل می‌دهند. اگر هیچ راس برشی در گراف وجود نداشته باشد، گراف دو همبند است و بنابراین، یک مولفه دو همبند وجود دارد که خود گراف است.

برنامه تشخیص مولفه دو همبند در ++C

برنامه تشخیص مولفه دو همبند در جاوا

برنامه تشخیص مولفه دو همبند در پایتون

خروجی قطعه کدهای بالا به صورت زیر است.

4--2 3--4 3--1 2--3 1--2
8--9
8--5 7--8 5--7
6--0 5--6 1--5 0--1 
10--11
Above are 5 biconnected components in graph

اگر نوشته بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های برنامه‌‌ نویسی
• آموزش ساختمان داده‌ها
• مجموعه آموزش‌های ساختمان داده و طراحی الگوریتم
• برنامه تشخیص وجود دور در گراف جهت‌دار — راهنمای کاربردی
• برنامه بررسی وجود دور در گراف بدون جهت — راهنمای کاربردی
• یافتن دور همیلتونی با الگوریتم پس گرد — به زبان ساده
• الگوریتم بازی مار و پله همراه با کد — به زبان ساده
• حل مساله n وزیر با الگوریتم پس‌گرد (Backtracking) — به زبان ساده

^^