هر عدد به توان صفر | صفر به توان هر عدد — به زبان ساده و با مثال

در این آموزش از مجله فرادرس می‌خواهیم درباره چند مورد از پرسش‌های رایج دانش‌آموزان در درس ریاضی بحث کنیم؛ پرسش‌هایی از قبیلِ نتیجه هر عدد به توان صفر چیست؟ صفر به توان هر عدد چگونه محاسبه می‌شود؟ حاصل صفر به توان صفر چیست؟

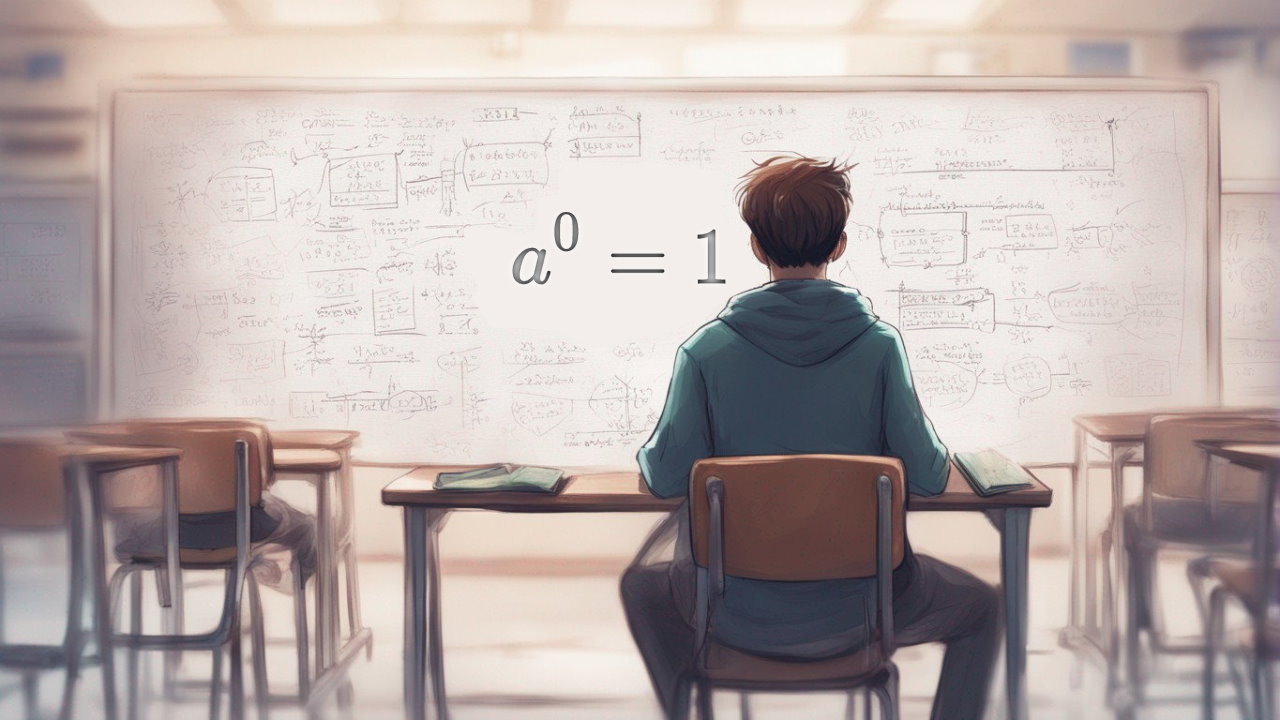
هر عدد به توان صفر

حاصل هر عدد به توان صفر برابر با یک است. البته در اینجا منظورمان عددی غیر از صفر است. این یعنی اینکه برای عدد غیرصفر $$a\neq 0$$، می‌توان چنین نوشت:

$$\large \boxed { a ^ 0 = 1 }$$

فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم در فرادرس

کلیک کنید

برای مثال، داریم:

$$\large \begin {align*} 0.0002 ^ 0 & = 1 \\ (-2.3) ^ 0 & = 1 \\ 6 ^ 0 & = 1 \\ 10000 ^ 0 & = 1 \\ ( - 1 ) ^ 0 & = 1 \\ 1 ^ 0 & = 1 \\ (-4528) ^ 0 & = 1 \\ 1.3 ^ 0 & = 1 \end {align*}$$

اما چرا هر عدد به توان صفر همیشه برابر با یک می‌شود؟‌ یکی از مواردی که برای پاسخ به این پرسش مطرح می‌شود، با بهره‌گیری از مفهوم توان در ریاضیات است. همان‌طور که می‌دانیم، در تقسیم دو عدد با پایه مشابه و توان متفاوت، پایه ثابت می‌ماند و توان‌ها از یکدیگر کم می‌شوند.

برای مثال، عدد دلخواه $$a$$ را در نظر بگیرید. حاصل تقسیم $$a^m$$ بر $$a^ n$$ به صورت زیر خواهد بود:

$$\large \frac { a ^ m } { a ^ n } = a ^ { m - n }$$

برای مثال، داریم:

$$\large \frac { 3 ^ 8 } { 3 ^ 6 } = 3 ^ { 8 - 6 } = 3 ^ 2 = 9$$

حال فرض کنید $$a$$ یک عدد صحیح غیرصفر باشد و $$n=m$$. بنابراین، می‌توان نوشت:

$$\large a ^ { m - m } = \frac { a ^ m } { a ^ m } = 1$$

یکی دیگر از راه‌هایی که می‌توان به این نتیجه رسید که هر عدد به توان صفر برابر با یک است، استفاده از قاعده ضرب اعداد توان‌دار است. همان‌طور که می‌دانیم، برای عدد صحیح غیرصفر $$a$$ و اعداد صحیح $$m$$ و $$n$$ می‌توان نوشت:

$$\large a ^ { m + n } = a ^ m a ^ n$$

 با قرار دادن $$m = 1$$ و $$n= 0$$، داریم:

$$\large a ^ { 1 + 0 } = a ^ 1 a ^ 0$$

و در نتیجه:

$$\large a ^ 1 = a ^ 1 a ^ 0$$

با تقسیم طرفین بر $$a ^ 1$$، می‌توان نوشت:

$$\large \frac { a ^ 1 } { a ^ 1 } = \frac {a ^ 1 a ^ 0 } { a ^ 1 }$$

بنابراین، به تساوی زیر می‌رسیم که نشان می‌دهد هر عدد به توان صفر برابر با یک است:

$$\large 1 = a ^ 0$$

برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

یکی از راه‌هایی شهودی که می‌توانید مقدار هر عدد به توان صفر را تخمین بزنید، استفاده از ماشین حساب است. اما چگونه؟ برای مثال، به جای عدد صفر عددی بسیار کوچک و نزدیک به صفر در نظر بگیرید و محاسبه را در ماشین‌حساب انجام دهید. اگر مثلاً عدد ۵ را به توان عدد بسیار کوچک ۰٫۰۰۰۰۰۰۰۰۰۳ برسانید، عدد زیر به دست خواهد آمد که بسیار نزدیک به ۱ است.

صفر به توان هر عدد

اگر $$n$$ یک عدد صحیح مثبت و غیرصفر باشد. در این صورت، صفر به توان هر عدد برابر با صفر خواهد بود. یعنی، داریم:

$$0 ^ n = 0$$

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

این تساوی واضح به نظر می‌رسد. زیرا، داریم:

$$\large \begin {align*} & n = 1 \rightarrow 0 ^ 1 = 0 \\ & n = 2 \rightarrow 0 ^ 2 = 0 \times 0 = 0 \\ & n = 3 \rightarrow 0 ^ 3 = 0 \times 0 \times 0= 0 \\ & \vdots \end {align*}$$

صفر به توان صفر

اگر دو بخش بالا را خوانده باشید، احتمالاً این پرسش برایتان پیش آمده که پس صفر به توان صفر چه می‌شود؟ چرا در دو بخش قبلی به آن نپرداختیم. واقعیت این است که برای پاسخ به این پرسش، دودستگی وجود دارد. عده‌ای صفر به توان صفر را مبهم می‌دانند و عده‌ای در برخی موارد آن را برابر با یک در نظر می‌گیرند و البته دلایل منطقی نیز برای آن دارند.

معمولاً در ریاضیات دانشگاهی و آنالیز ریاضی مقدار $$0 ^ 0$$، تعریف‌نشده و صورت مبهم در نظر گرفته می‌شود. دلیل این امر نیز نشان دادن این موضوع است که برای مثال، تابع $$x ^ y$$ در نقطه $$( 0 , 0 )$$ نه مشتق‌پذیر و نه پیوسته است. البته قرار دادن صفر به توان صفر برابر با $$1$$ نیز مشکلی ایجاد نخواهد کرد.

برای آشنایی بیشتر با پاسخ صفر به توان صفر، پیشنهاد می‌کنیم به مطلب «صفر به توان صفر — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» از مجله فرادرس  مراجعه کنید.

جمع‌بندی

آنچه را که گفتیم، می‌توان در موارد زیر خلاصه کرد:

1. هر عدد صحیح غیرصفر به توان صفر برابر با یک است.
2. صفر به توان یک عدد صحیح مثبت برابر با صفر است.
3. صفر به توان صفر معمولاً در آنالیز ریاضی (حسابان) مبهم است، اما در جبر، ترکیبیات، یا نظریه مجموعه‌ها، برابر با یک در نظر گرفته می‌شود.