نمونه برداری سیگنال – راهنمای جامع
نمونه برداری سیگنال (Signal Sampling) یکی از مباحث مهم در پردازش سیگنال است. در این مطلب ابتدا به بیان قضیه نمونه برداری نایکویست (Nyquist Theorem) و اثبات آن میپردازیم و سپس تکنیکهای نمونه برداری از سیگنالها را بیان میکنیم.
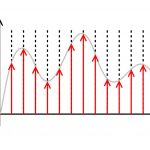
بیان قضیه نایکوئیست در نمونه برداری سیگنال
یک سیگنال پیوسته در زمان را میتوان توسط نمونههای (Samples) آن نمایش داد. بر اساس قضیه نمونه برداری سیگنال نایکویست یا نایکوئیست-شانون، عکس این عمل، یعنی ساخت مجدد سیگنال اصلی از روی سیگنال نمونه برداری شده، در شرایطی امکانپذیر است که فرکانس نمونه برداری بزرگتر یا مساوی با دو برابر بزرگترین مولفه فرکانسی سیگنال پیام یا سیگنال اصلی باشد.
بنابراین شرط زیر باید در نمونه برداری برقرار باشد:
اثبات قضیه نایکوئیست
یک سیگنال پیوسته در زمان را در نظر بگیرید. طیف فرکانسی این سیگنال در محدوده باند هرتز قرار دارد. به عبارت دیگر، طیف فرکانسی سیگنال برای برابر با صفر است.
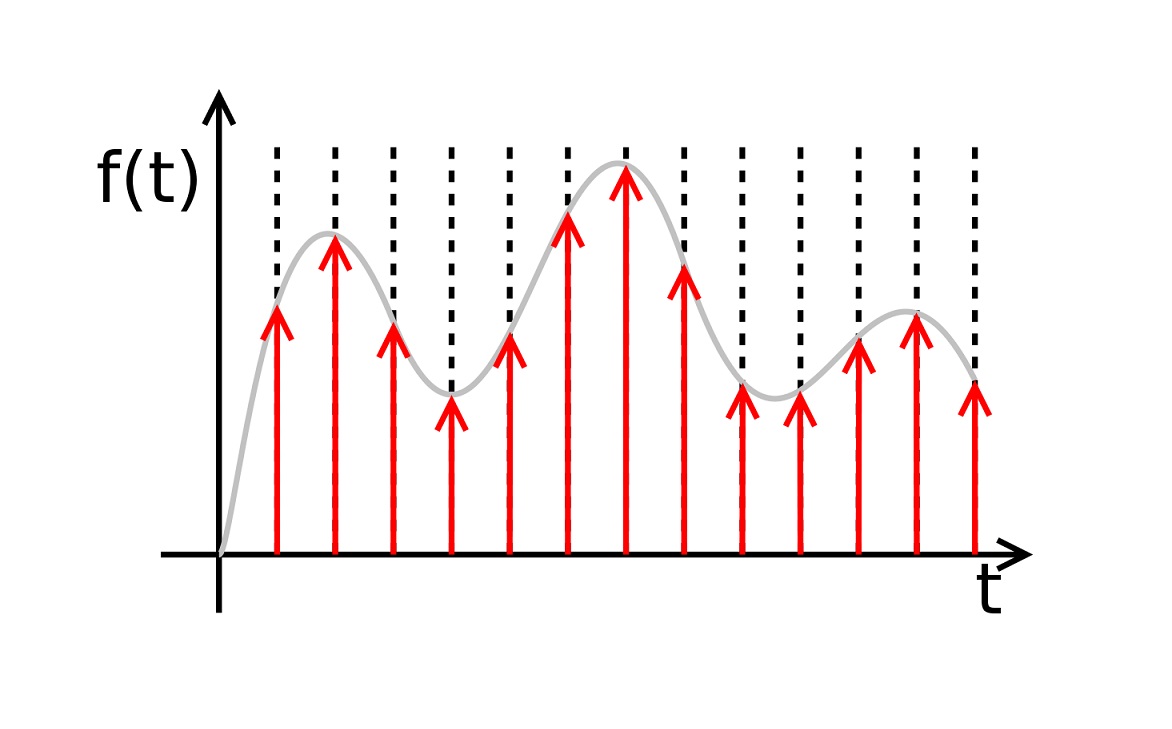
برای نمونه برداری از سیگنال ورودی باید این سیگنال را در قطار ضربه با تناوب ضرب کرد. خروجی ضربکننده یک سیگنال گسسته است که سیگنال نمونه برداری شده نام دارد. سیگنال نمونه برداریشده را با نمایش میدهند. در تصویر زیر نمایی از نحوه نمونه برداری از یک سیگنال پیوسته در زمان را میتوان مشاهده کرد.
با توجه به تصاویر بالا میتوان به این نکته پی برد که سیگنال نمونه برداری شده فرکانس و دوره تناوبی برابر با دوره تناوب و فرکانس سیگنال ضربه را به دست خواهد آورد.
روند نمونه برداری از یک سیگنال پیوسته در زمان را با استفاده از فرمول زیر نیز میتوان نشان داد:
نمایش سری فوریه مثلثاتی تابع ضربه به صورت زیر خواهد بود:
در فرمول بالا داریم:
با جایگذاری مقادیر بالا در معادله شماره ۲ داریم:
همچنین با جایگذاری در معادله شماره ۱ داریم:
از هر دو طرف رابطه بالا تبدیل فوریه میگیریم. در نتیجه معادله زیر را به دست میآوریم:
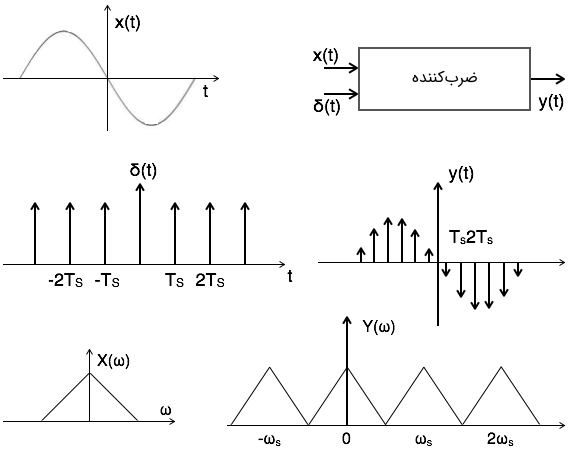
برای بازسازی ، باید طیف فرکانسی سیگنال ورودی () را از روی طیف فرکانسی سیگنال نمونه برداری شده () به دست آورد. این عمل زمانی امکان پذیر است که بین تناوبهای هیچ همپوشانی (Overlapping) وجود نداشته باشد. در تصویر زیر نمایی از امکان به دست آوردن طیف فرکانسی سیگنال اصلی از روی طیف فرکانسی سیگنال نمونه برداری شده نشان داده شده است. بر این اساس نمونه برداری از یک سیگنال را به سه دسته بیشنمونه برداری، نمونه برداری ایدهآل و کمنمونه برداری تقسیم میکنند.
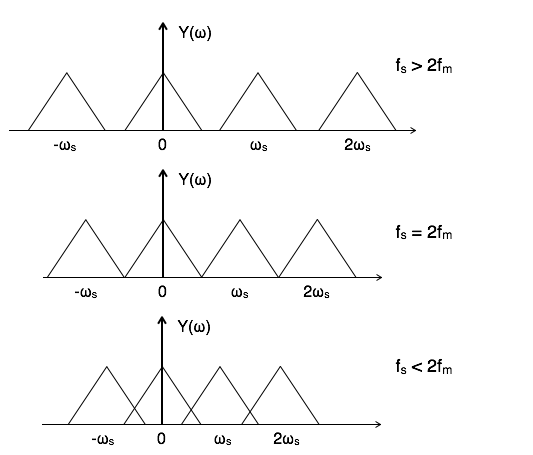
در تصویر اول، است و به اصطلاح بیش نمونه برداری (Over Sampling) اتفاق افتاده است. در تصویر دوم، است و در این حالت نمونه برداری ایدهآل انجام گرفته است. اما در تصویر سوم، است که در این حالت کمنمونه برداری (Under Sampling) به وقوع پیوسته است.
اثر تداخل
در حالت کمنمونه برداری، ناحیه دارای همپوشانی نشاندهنده اثر تداخل یا در همروی (Aliasing Effect) است. به عبارت دیگر، زمانی که فرکانس نمونه برداری یعنی از دو برابر پهنای باند سیگنال یعنی بیشتر باشد، پدیده تداخل اتفاق میافتد. در این حالت به راحتی میتوان سیگنال اصلی را با استفاده از یک فیلتر پایین گذر ایدهآل جداسازی کرد. راه حل دیگر برای حذف کردن اثر تداخل در نمونه برداری این است که فرکانس سیگنال اصلی را بیشتر از دو برابر فرکانس سیگنال ضربه در نظر بگیریم.
تکنیکهای نمونه برداری
در حالت کلی میتوان گفت که سه تکنیک اساسی برای نمونه برداری از سیگنال وجود دارد.
- نمونه برداری تابع ضربه (Impulse Sampling)
- نمونه برداری طبیعی (Natural Sampling)
- نمونه برداری بالا مسطح (Flat Top Sampling)
نمونه برداری سیگنال با استفاده از تابع ضربه
همان طور که در بالا نیز بیان کردیم، نمونه برداری سیگنال به روش تابع ضربه را میتوان از طریق ضرب کردن سیگنال اصلی در قطار تابع ضربه با تناوب T به دست آورد. در این حالت، دامنه ضربهها متناسب با دامنه سیگنال اصلی ورودی تغییر میکنند. این نوع نمونه برداری در تصویر زیر نشان داده شده است.
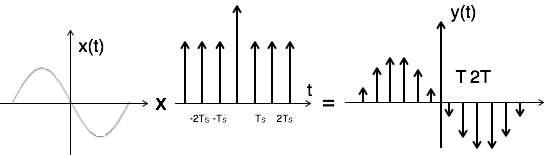
سیگنال خروجی نمونه برداری را در این حالت توسط فرمول زیر به دست میآورند:
برای به دست آوردن طیف فرکانس سیگنال نمونه برداری شده، بر روی دو سمت معادله بالا تبدیل فوریه اعمال میکنیم:
این نوع نمونه برداری، نمونه برداری ایدهآل یا نمونه برداری تابع ضربه نام دارد. اما مشکلی که وجود دارد این است که از این نوع نمونه برداری در عمل نمیتوان استفاده کرد؛ زیرا عرض پالسها در عمل نمیتواند برابر با صفر شود و به همین دلیل تولید قطار ضربه به صورت عملی و در واقعیت امکانپذیر نیست.
نمونه برداری سیگنال طبیعی
نمونه برداری سیگنال طبیعی مشابه با نمونه برداری تابع ضربه است، با این تفاوت که به جای توابع ضربه از قطار پالسها با تناوب T استفاده میکند. به عبارت دیگر، در این نمونه برداری سیگنال ورودی در قطار پالس ضرب میشود. در تصویر زیر، نمایی از فرایند نمونه برداری طبیعی نشان داده شده است.
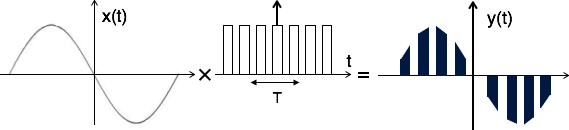
خروجی نمونه برداری به صورت زیر خواهد بود:
نمایش سری فوریه نمایی را میتوان به صورت زیر نوشت:
که در این فرمول داریم:
با جایگذاری مقادیر در معادله شماره ۴ داریم:
با جایگذاری در معادله شماره ۳ داریم:
برای به دست آوردن طیف سیگنال نمونه برداری شده، باید از هر دو طرف معادله بالا تبدیل فوریه بگیریم. در نتیجه داریم:
بر اساس مشخصه انتقال فرکانسی (Frequency Shifting) میتوان نوشت:
نمونه برداری سیگنال بالا مسطح
در طول انتقال سیگنال، این امکان وجود دارد که نویزهای ناخواسته به سطح بالایی سیگنال اضافه شوند. در این حالت، اگر سیگنال از فرم بالا مسطح باشد، میتوان به سادگی آنها را حذف کرد. در این جا سطح بالای نمونهها صاف است، به عبارت دیگر، پالسها دارای دامنه ثابت هستند. نمونه برداری بالا مسطح از نمونهها و نیز مدارات نگهدار استفاده میکند. در تصویر زیر نمونهای از فرایند نمونه برداری بالا مسطح نشان داده شده است.
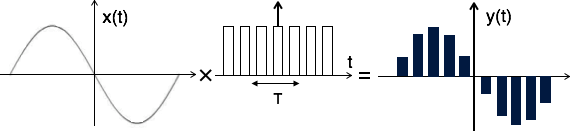
از نظر تئوری، سیگنال نمونه برداری شده را میتوان از طریق کانولوشن پالس مستطیلی با سیگنال نمونه برداری شده ایدهآل به دست میآید. بنابراین سیگنال خروجی به صورت زیر به دست میآید:
در تصویر زیر نیز دیاگرام این کار نشان داده شده است.
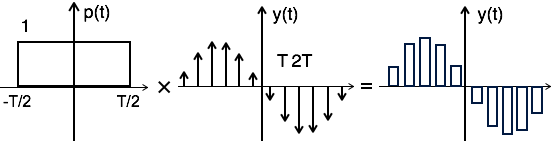
برای به دست آوردن طیف فرکانسی سیگنال نمونه برداری شده، از هر دو طرف معادله بالا تبدیل فوریه میگیریم. بنابراین داریم:
با استفاده از مشخصه کانولوشن میتوانیم بنویسیم:
در نتیجه داریم:
نرخ نایکویست در نمونه برداری سیگنال
بر اساس قضیه نایکوئیست-شانون، یک نرخ نمونه برداری کمینه وجود دارد که در آن میتوان یک سیگنال پیوسته را به نمونههای آن تبدیل کرد و نیز بدون اعوجاج آنها را بازیابی کرد.
این نرخ را نرخ نایکویست میگویند که به صورت زیر است:
همچنین بازه نایکویست (Nyquist Interval) برابر است با:
نمونه برداری سیگنال میان گذر
در مورد سیگنالهای میان گذر (Band Pass Signals)، طیف فرکانسی این سیگنالها برای فرکانسهای خارج از برابر با است. فرکانس همیشه بزرگتر از صفر است. همچنین، زمانی که باشد، اثر تداخل در سیگنال خروجی وجود نخواهد داشت. اما دو عیب اساسی در این شرایط وجود دارد:
- نرخ نمونه برداری نسبت به بزرگ است که باعث میشود یک محدودیت در کاربردهای عملی محسوب شود.
- طیف فرکانسی سیگنال نمونه برداری شده دارای گپهای طیفی خواهد بود.
برای غلبه بر این مشکلات، قضیه میان گذر (Band Pass Theorem) بیان میکند که اگر فرکانس نمونه برداری باشد، آنگاه سیگنال ورودی را میتوان نمونه برداری کرد و سپس مجددا از روی سیگنال نمونه برداری شده بدون اعوجاج بازیابی کرد. همچنین:
که در این فرمول m برابر با بزرگترین عدد صحیح است که کوچکتر از باشد. B در این فرمول پهنای باند سیگنال است. اگر باشد، آنگاه داریم:
برای سیگنالهای میان گذر با پهنای باند و کمینه نرخ نمونه برداری ، طیف فرکانسی سیگنال نمونه برداری شده به صورت زیر به دست میآید:
نمونه برداری سیگنال در متلب
در این قسمت میخواهیم نحوه ایجاد کردن یک سیگنال پیوسته در زمان و نمونه برداری از آن با یک نرخ معین را نشان دهیم. در بسیاری از کاربردهای شبیهسازی، ممکن است لازم باشد تا یک سیگنال پیوسته در زمان را از طریق نمونه برداری صحیح به یک سیگنال گسسته در زمان تبدیل کنیم.
همان طور که بیان کردیم، برای یک سیگنال باند پایه پیوسته در زمان باید از قضیه نمونه برداری نایکوئیست-شانون استفاده و نرخ نمونه برداری را توسط آن تعیین کرد. بر اساس این قضیه، حداقل فرکانس نمونه برداری باید بزرگتر از دو برابر فرکانس بیشینه سیگنال اصلی باشد. نرمافزار متلب یا هر نرمافزار شبیهسازی دیگر، تمام پردازشها را به صورت گسسته در زمان انجام میدهد؛ زیرا سیگنالها در حافظه کامپیوتر به صورت گسسته در زمان نشان داده میشوند.
بنابراین نمیتوان یک سیگنال پیوسته در زمان واقعی را در کامپیوتر تولید کنیم و تنها کاری که باید انجام داد این است که از طریق اتخاذ نرخ نمونه برداری بسیار بالا، یک سیگنال شبه پیوسته (Continuous-Like) ایجاد کنیم. چنین سیگنالی پس از رسم شدن بسیار شبیه به یک سیگنال پیوسته در زمان خواهد بود. حال میخواهیم در نرمافزار متلب یک سیگنال سینوسی شبه پیوسته با فرکانس تولید کنیم. برای اینکه سیگنال هنگام ترسیم پیوسته به نظر برسد، نرخ نمونه برداری برابر با در نظر میگیریم.
قطعه کد زیر نحوه انجام این کار در متلب را نشان میدهد.
نمودار زیر در خروجی ترسیم میشود.
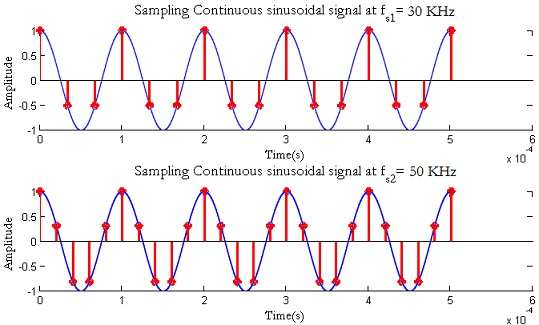
حال میخواهیم سیگنال پیوسته در زمان بالا را با استفاده از قضیه نمونه برداری نایکوئیست-شانون به یک سیگنال در حوزه گسسته در زمان تبدیل کنیم. در نتیجه فرکانس نمونه برداری حداقل باید باشد. به عنوان مثال، ابتدا سیگنال را با فرکانس و سپس با فرکانس نمونه برداری میکنیم.
برای نمونه برداری سیگنال، قطعه کد زیر را در محیط متلب اجرا میکنیم.
در تصویر زیر سیگنال گسسته ایجاد شده پس از نمونه برداری در دو فرکانس مختلف نشان داده شده است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی مخابرات
- آموزش مخابرات ۱
- مجموعه آموزشهای پردازش سیگنال
- آموزش تجزیه و تحلیل سیگنال ها و سیستم ها
- مدولاسیون دامنه — از صفر تا صد
- دمدولاسیون دامنه — از صفر تا صد
- انرژی و توان سیگنال — از صفر تا صد
^^













اگر فقط دو تا مثال عددی هم حل می کردید عالی میشد
خیلی عالی
سلام. مرجع مطالب بالا را لطفا بفرمایید.
با سلام؛
منبع تمامی مطالب مجله فرادرس، اگر ترجمه باشند، در انتهای مطلب و پیش از نام نویسنده آورده شدهاند.
با تشکر از همراهی شما با مجله فرادرس
از مطلب پر کاربرد شما بسیار سپاسگزارم