نامساوی نمایی – به زبان ساده

نامساوی نمایی یک نامساوی ریاضی است که در آن، یک (یا هر دو) طرف نامساوی یک متغیر نمایی دارند. این‌ نامساوی‌ها در موقعیت‌هایی که ضرب مکرر وجود دارد، مفید هستند، به ویژه وقتی که با یک مقدار ثابت مانند نرخ بهره مقایسه شوند. به عنوان مثال، برای آنکه مشخص گردد که چه مدت طول می‌کشد تا پول افراد بر اساس نرخ سود مشخصی دو برابر شود، از نامساوی نمایی استفاده می‌شود. مثلاً، تقریباً ۱۲ سال طول خواهد کشید تا پول با نرخ سود ثابت ۶ درصد دو برابر شود.

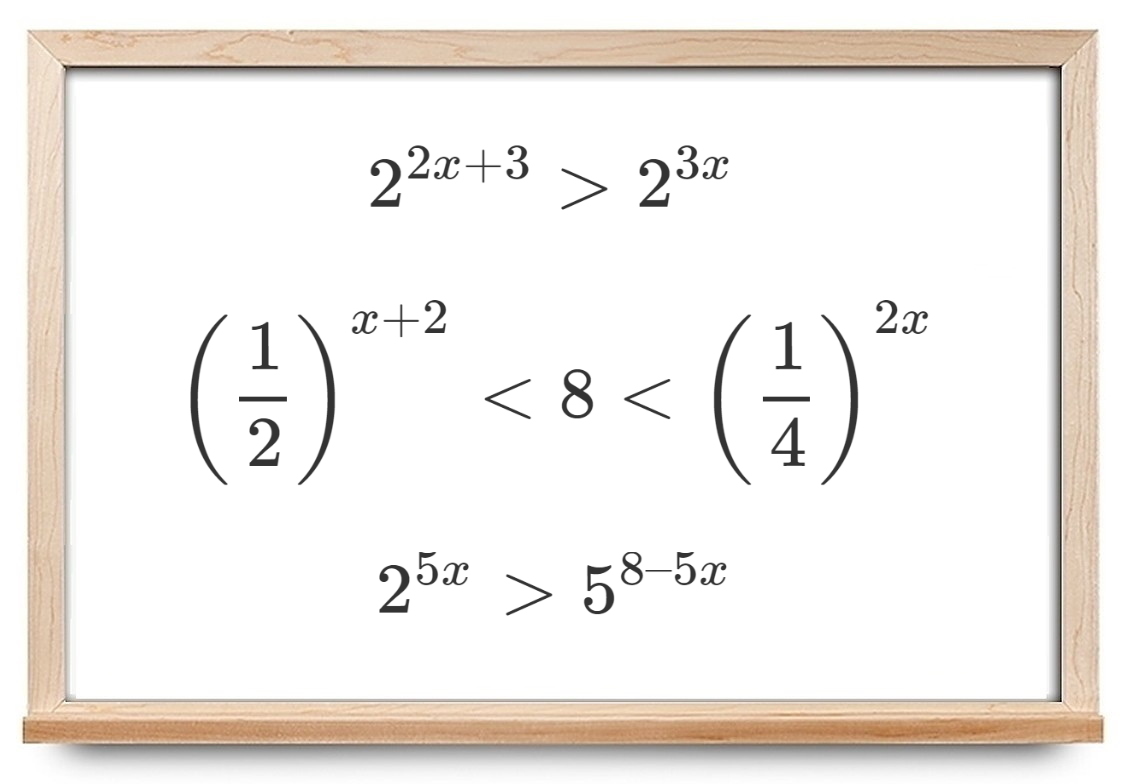
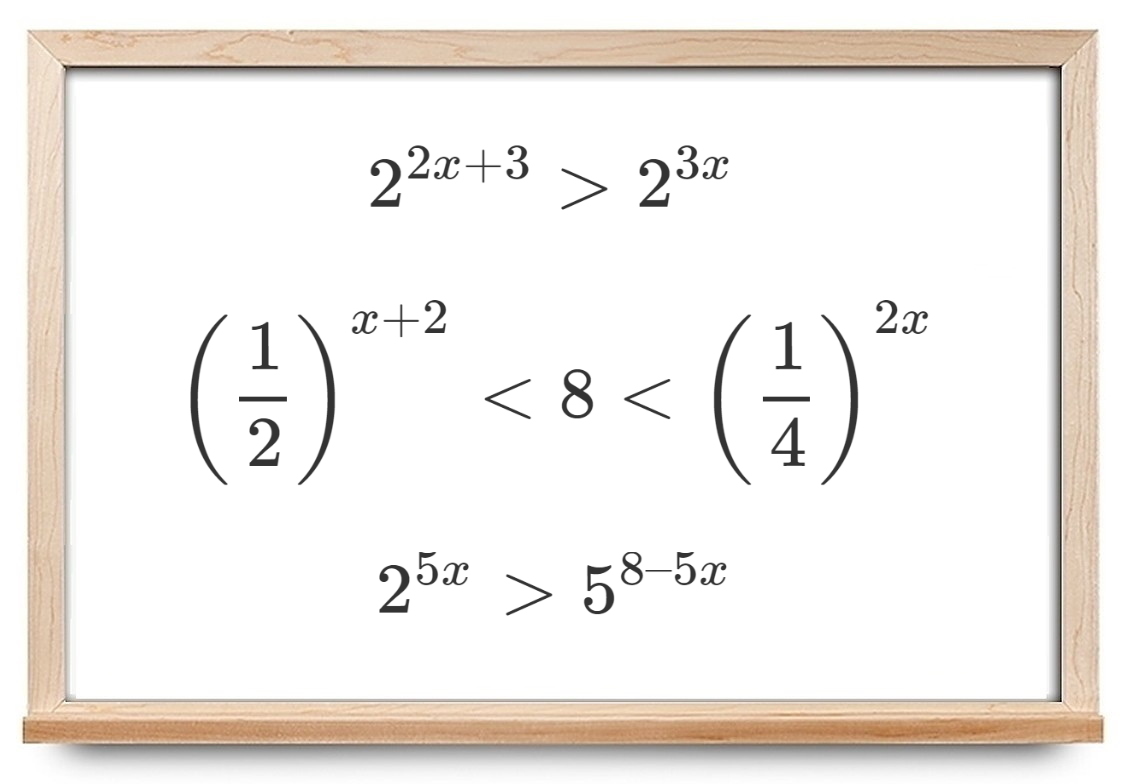
نامساوی نمایی

نکته کلیدی کار با نامساوی نمایی، گزاره زیر است:

اگر $$a > 1$$ و $$x > y$$ باشد، آنگاه $$a ^ x > a ^ y$$ است. برعکس، اگر $$0 < a < 1$$، آنگاه $$a ^ x < a ^ y$$ خواهد بود.

اگر $$a = 1$$ باشد، آنگاه $$1 ^ x = 1$$ است و به طور مشابه، اگر $$a = 0$$، آنگاه $$0 ^ x = 0$$ خواهد بود ($$x$$ هر عدد مثبتی است). مهم‌تر از همه، عبارت زیر صحیح است:

اگر $$a > 1$$ و $$a ^ x > a ^ y$$ باشد× آنگاه $$x > y$$ خواهد بود. برعکس، اگر $$0 < a < 1$$ و $$a ^ x > a ^ y$$ باشد، آنگاه $$x < y$$ است.

به بیان رسمی‌تر، $$f ( x ) = a ^ x$$ به ازای $$a > 1$$ صعودی یکنوا (افزایش $$x$$ همواره سبب افزایش $$f ( x )$$ می‌شود) و برای $$0< a < 1$$ نزولی یکنواست (با افزایش $$x$$، مقدار $$f (x)$$ همواره کاهش می‌یابد).

خوشبختانه، هر دو مورد به صورت شهودی قابل درک است؛ وقتی مبنا یا پایه بزرگ‌تر از ۱ باشد، آن سمتی که نمای بزرگ‌تری دارد، بزرگ‌تر خواهد بود. برعکس این گفته برای وقتی که پایه کوچک‌تر از ۱ باشد، صحیح است. برای مثال، بدون داشتن هرگونه دانشی از گزاره‌هایی که در بالا بیان کردیم، به طور شهوی انتظار داریم $$2 ^ {100}$$ بزرگ‌تر از $$2 ^ { 95 }$$ باشد.

نامساوی نمایی با پایه مشابه

وقتی دو طرف نامساوی دارای پایه مشابه باشند، از گزاره‌ای که در ابتدای متن معرفی کردیم، استفاده می‌کنیم.

مثال ۱: مقدار $$x$$ در نامساوی زیر در چه بازه‌ای است؟

$$\large 2 ^ { 2 x + 3 } > 2 ^ { 3 x }$$

حل: از آنجا که پایه $$2$$ است (بزرگ‌تر از $$1$$)، نامساوی $$2 ^ { 2 x + 3 } > 2 ^ { 3 x }$$ منجر به نامعادله $$2 x + 3 > 3 x$$ می‌شود. با کم کردن $$2 x$$ از دو طرف نامساوی، به $$3 > x$$ می‌رسیم. بنابراین، جواب نامعادله، $$x$$های کوچک‌تر از $$3$$ است.

مثال ۲: به ازای چه مقادیری از $$x$$ نامعادله زیر برقرار است؟

$$\large 2^ { 3 ^ { 4 x + 1 } } > 2 ^ {3 ^{ 2 x+ 3 } }$$

حل: از آنجا که پایه برابر با $$2$$ و کوچک‌تر از $$1$$ است، نامساوی $$3 ^ { 4 x + 1 } > 3 ^ { 2 x + 3 }$$ را خواهیم داشت. در نتیجه، نامساوی $$4 x + 1 > 2 x + 3$$ یا $$2 x > 2 \implies x > 1$$ را داریم. بنابراین، همه $$x$$های بزرگ‌تر از $$1$$ در نامعادله اصلی صدق می‌کنند.

نامساوی نمایی با پایه کوچک‌تر از یک

در حالتی که پایه کوچک‌تر از یک باشد، آنچه پیش‌تر گفتیم برعکس می‌شود؛ طرف بزرگ‌تر اکنون آن است که نمای کوچک‌تری داشته باشد.

مثال ۱: چه مقادیری از $$x$$ در نامعادله زیر صدق می‌کنند؟

$$\large \left ( \frac { 1 } { 2 } \right ) ^ { 3 x } > \left ( \frac { 1 } { 2 } \right ) ^ { 2 x + 3 }$$

حل: از آنجا که پایه برابر با $$\frac 12$$ و کوچک‌تر از $$1$$ است، نامساوی $$3 x < 2 x + 3$$ را خواهیم داشت که برای همه $$x$$های کوچک‌تر از $$3$$ برقرار است.

نامساوی نمایی با پایه متفاوت

گاهی پایه‌ها ظاهراً متفاوت هستند، اما می‌توان آن‌ها را به یک پایه یکسان تبدیل کرد.

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

مثال ۱: نامعادله زیر را حل کنید.

$$\large 4 ^ { x + 2 } > 8 ^ { 2 x }$$

حل: می‌بینیم که پایه‌ها متفاوت هستند، اما می‌توان آن‌ها را با استفاده از روابط $$4=2^2$$ و $$8=2^3$$ به یک پایه مشابه تبدیل کرد. با بازنویسی نامساوی با پایه $$2$$، خواهیم داشت:

$$\large 2 ^ { 2 ( x + 2 ) } > 2 ^ { 3 ( 2 x ) } \implies 2 ^ { 2 x + 4 } > 2 ^ { 6 x }$$

بنابراین، $$2 x + 4 > 6 x$$ است و نتیجه نهایی $$1 > x$$ را حاصل می‌کند. بنابراین، جواب نامساوی نمایی، همه $$x$$های کوچک‌تر از $$1$$ است.

مثال ۲: جواب نامعادله زیر را محاسبه کنید.

$$\large 1 6 ^ x > 2 ^ 2 \cdot 4 ^ 3 \cdot 8 ^ 4$$

حل: همه پایه‌ها را به $$2$$ تبدیل می‌کنیم:

$$\large \big ( 2 ^ 4 \big ) ^ x > 2 ^ 2 \cdot \big ( 2 ^ 2 \big ) ^ 3 \cdot \big ( 2 ^ 3 \big ) ^ 4 \implies 2 ^ { 4 x } > 2 ^ 2 \cdot 2 ^ 6 \cdot 2 ^ { 1 2 } = 2 ^ { 2 0 } .$$

بنابراین، $$4 x > 2 0 \implies x > 5$$. در نتیجه، جواب همه $$x$$های بزرگ‌تر از $$5$$ است.

وقتی دو پایه متفاوت باشند و نتوان آن‌ها را به یک پایه یکسان تبدیل کرد، استفاده از لگاریتم ضروری خواهد بود. خوشبختانه، لگاریتم‌ها اساساً ویژگی‌های مشابهی با توابع نمایی دارند:

اگر $$a > 1$$ و $$x > y$$ باشد، آنگاه $$\log _ a x > \log _ a y$$. برعکس، اگر $$0 < a < 1$$ باشد، آنگاه $$\log _ a x < \log _ a y$$ خواهد بود.

گزاره زیر نیز صحیح است:‌

اگر $$a > 1$$ و $$\log _ a x > \log _ a y$$، آنگاه $$x > y$$ است. برعکس، اگر $$0 < a < 1$$ باشد نیز $$x < y$$ را خواهیم داشت.

مثال ۳: چه مقادیری از $$x$$ در نامساوی زیر صدق می‌کنند؟

$$\large 2 ^ { 5 x } > 5 ^ { 8 - 5 x }$$

حل: از دو طرف نامساوی لگاریتم (مبنای ۱۰) می‌گیریم و خواهیم داشت:

$$\large \log 2 ^ { 5 x } > \log 5 ^ { 8 - 5 x } \implies 5 x \log 2 > ( 8 - 5 x ) \log 5$$

بنابراین، $$5 x \log 2 > 8 \log 5 - 5 x \log 5$$. با بازآرایی این نامعادله، $$5 x ( \log 2 + \log 5 ) > 8 \log 5$$ را داریم. از آنجا که $$\log 2 + \log 5 = \log 1 0 = 1$$، نامساوی $$5 x > 8 \log 5$$ و در نتیجه، $$x > \frac { 8 } { 5 } \log 5$$ را خواهیم داشت.

نامساوی نمایی با چند عبارت

در حالتی که چند عبارت داشته باشیم، باید یک متغیر دیگر را به عبارت نمایی اختصاص دهیم و نتیجه را حل کنیم. در نتیجه این کار، با نامعادله‌ای با یک عبارت کار خواهیم کرد.

مثال ۱: نامعادله زیر را حل کنید:

$$\large 2 ^ x + 4 ^ x > 6$$

حل: فرض کنید $$y = 2 ^ x$$ باشد، به طوری که $$y + y ^ 2 > 6$$. این را می‌توان به صورت $$y ^ 2 + y - 6 = ( y - 2 ) ( y + 3 ) > 0$$ بازآرایی کرد که وقتی $$y > 2$$ یا $$y < - 3$$ باشد، برقرار است. از آنجا که $$2 ^ x$$ نمی‌تواند منفی باشد، در نتیجه، $$y > 2 \implies 2 ^ x > 2 ^ 1$$ را خواهیم داشت که $$x > 1$$ را نتیجه می‌دهد. بنابراین، همه $$x$$های بزرگ‌تر از $$1$$ در نامساوی اصلی صدق می‌کنند.

مثال ۲: نامعادله زیر را حل کنید.

$$\large \left ( \frac { 1 } { 2 } \right ) ^ { x + 2 } < 8 < \left ( \frac { 1} { 4 } \right ) ^ { 2 x }$$

حل: نامعادله اول $$\left ( \frac { 1 } { 2 } \right ) ^ { x + 2 } < 8$$ یا $$\left ( \frac { 1 } { 2 } \right ) ^ { x + 2 } < \left ( \frac { 1 } { 2 } \right ) ^ { - 3 }$$ خواهد بود. از آنجا که $$\frac 12$$ کوچک‌تر از $$1$$ است، در نتیجه، نامساوی $$x + 2 > - 3$$ یا $$x > - 5$$ را خواهیم داشت.

نامساوی دوم $$8< \left ( \frac { 1 } { 4 } \right ) ^ { 2 x }$$ یا $$\left ( \frac { 1 } { 2 } \right ) ^ { - 3 } < \left ( \frac { 1 }{ 2 } \right ) ^ { 4 x }$$ است. در نتیجه، $$- 3 > 4 x$$ یا معادل آن، $$- \frac { 3 } { 4 } > x$$ را داریم.

با کنار هم قرار دادن دو نامعادله در کنار یکدیگر، جواب مجموعه $$- 5 < x < - \frac { 3 } { 4 }$$ است.

حل مسائل نامساوی نمایی

یک استراتژی کلیدی برای حل نامساوی نمایی به توان رساندن دو طرف به نمای عددی یکسان است تا مسئله ساده شود.

مثال ۱: بزرگ‌ترین عدد صحیح $$x$$ را بیابید که در نامعادله زیر صدق می‌کند:

$$\large 3 ^ { 2 0 } > 3 2 ^ x$$

حل: از آنجا که $$32 = 2 ^ 5$$، نامساوی را می‌توان به صورت $$3 ^ { 2 0 } > 2 ^ { 5 x } \implies \big ( 3 ^ 4 \big ) ^ 5 > \big ( 2 ^ x \big ) ^ 5$$  نوشت. این بدین معنی است که $$3 ^ 4 > 2 ^ x$$ است و با به توان $$\frac 15$$ رساندن دو طرف نامعادله به دست آمده است. از آنجا که $$3 ^ 4 = 81$$، بزرگ‌ترین عدد صحیح ممکن $$6$$ خواهد بود. از سوی دیگر، $$3 ^ 4 > 2 ^ x$$ نتیجه می‌دهد که $$\log _ 2 ( 3 ^ 4 ) > x \implies 4 \log _ 2 3 > x$$ و از آنجا که $$4 \log _ 2 3 \approx 6 . 3 4 4$$، بزرگ‌ترین عدد صحیح ممکن برای $$x$$، برابر با $$6$$ خواهد بود.

مثال ۱: نامعادله زیر را حل کنید.

$$\large ( x ^ 2 + x - 2 ) ^ { x ^ 2 - x - 2 } > 0 .$$

حل: مسئله را به چند قسمت بر اساس پایه $$x ^ 2 + x - 2$$ تقسیم می‌کنیم.

حالت ۱: اگر $$x ^ 2 + x - 2$$ مثبت باشد، آنگاه نامعادله بدون توجه به نما، درست خواهد بود. بنابراین، اولین حالت برای حل به صورت زیر است:

$$\large x ^ 2 + x - 2 > 0 \implies ( x + 2 ) ( x - 1 ) > 0 \implies x > 1 \text { or } x < - 2 .$$

حالت ۲: اگر $$x ^ 2 + x - 2$$ برابر با صفر باشد، آنگاه عبارت نمی‌تواند مثبت باشد. بنابراین، جواب وجود نخواهد داشت.

حالت ۳: اگر $$x ^ 2 + x - 2$$ منفی باشد، آنگاه $$x \in ( - 2 , 1 )$$.

برای آنکه $$( x ^ 2 + x - 2 ) ^ { x ^ 2 - x - 2 }$$ مثبت باشد، باید $$x ^ 2 - x - 2$$ یک عدد صحیح زوج باشد. مقادیر $$x ^ 2 - x - 2$$ روی دامنه محدود شده $$x \in (-2,1)$$ برابر با $$[-\frac 9 4 , 4 )$$ است. بنابراین، تنها مقادیر ممکن برای آنکه $$x ^ 2 - x - 2$$ یک عدد صحیح مثبت باشد، $$- 2$$، $$0$$ یا $$2$$ است.

اگر $$x ^ 2 - x - 2 = - 2$$، آنگاه $$x ^ 2 - x = 0 \implies x = 0 , 1$$. از آنجا که $$0, 1 \in [ - 2 , 1 ]$$، این جواب‌ها معتبر هستند.

اگر $$x ^ 2 - x - 2 = 0$$، آنگاه $$( x - 2 ) ( x + 1 ) = 0 \implies x = - 1 , 2$$. تنها $$- 1 \in [ - 2 , 1 ]$$، بنابراین، این تنها جواب در این زیرحالت است.

اگر $$x ^ 2 - x - 2 = 2$$ ، آنگاه $$x ^ 2 - x - 4 = 0 \implies x = \frac { 1 \pm \sqrt { 1 7 } } { 2 }$$. تنها $$\frac { 1 - \sqrt { 1 7 } } { 2 } \in [ - 2 , 1 ]$$. بنابراین، این تنها جواب در این حالت است.

با ترکیب این حالت‌ها، مجموعه جواب به صورت زیر خواهد بود:

$$\large x < - 2 ,\ x = \frac { 1 - \sqrt { 1 7 } } { 2 } ,\ x = - 1 , \ x = 0 , \ x > 1 .$$