معیار پایداری نایکویست در سیستم کنترل — از صفر تا صد

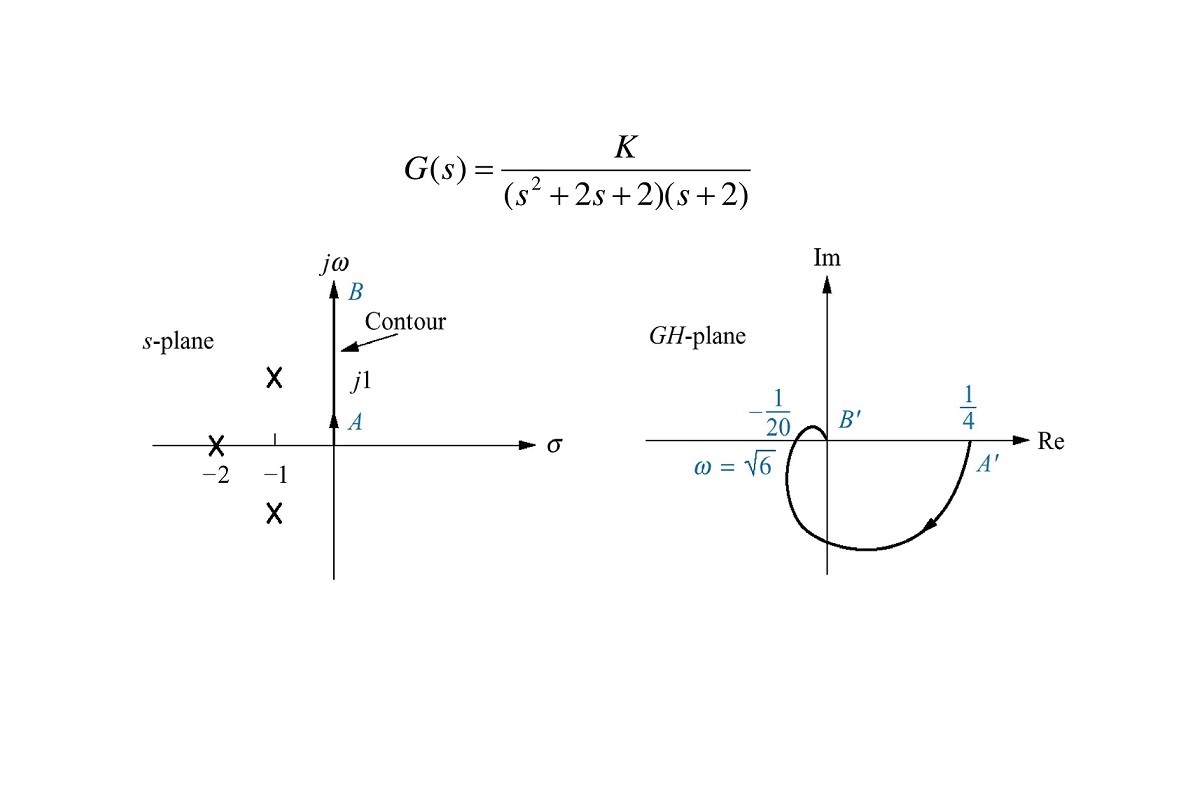
معیار پایداری نایکویست (Nyquist Stability Criterion) یک ابزار حوزه فرکانس است که برای بررسی پایداری سیستم‌های کانتوری مورد استفاده قرار می‌گیرد. برای استفاده از معیار پایداری نایکویست باید داده‌های پاسخ فرکانسی سیستم به صورت «نمودار قطبی» (Polar Plot) یا نمودار نایکویست ترسیم شوند. نمودار قطبی نموداری است که در آن دامنه و زاویه فاز به صورت تابعی از فرکانس بیان شده باشند. در این مطلب قصد داریم به بررسی معیار پایداری نایکویست بپردازیم.

قضیه نایکویست

در سال ۱۹۳۲ فردی به نام «نایکویست» از قضیه «کوشی» (Cauchy) استفاده کرد و در آن یک تابع از متغیرهای مختلط را در نظر گرفت تا به عنوان یک معیار در پایداری سیستم‌ها مورد استفاده قرار گیرد. قضیه کوشی مربوط به نگاشت «نواحی یا کانتورها» (Contours) از یک صفحه مختلط به صفحه‌ای دیگر است.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

به دلیل اینکه مطلوب است ریشه های معادله مشخصه در نیم صفحه راست محور $$ j \omega $$ قرار گیرد، ما کانتوری که کل نیم صفحه راست را احاطه می کند (توسط تابع تبدیل سیستم) نگاشت می‌دهیم. معادله مشخصه زیر را در نظر بگیرید:

$$ 1 + G H ( S ) = 0 $$

این معادله مشخصه در واقع یک تابع $$ F ( S ) $$ از متغیر مختلط S است که برابر با صفر قرار داده شده باشد:

$$ F ( S ) = 1 + G H ( S ) = 0 $$

معادله فوق را می‌توان به صورت زیر در نظر گرفت:

$$ F ( s ) = \frac { K \left ( s + z _ { 1 } \right) \left( s + z _ { 2 } \right) \cdots \left( s + z _ { n } \right)}{ \left ( s + p _ { 1 } \right) \left ( s + p _ { 2 } \right) \cdots \left ( s + p _ { m } \right ) } = 0 $$

در این رابطه، $$ z _ { i } $$ها برابر با ریشه‌های معادله مشخصه و $$ P _ { j } $$ها برابر با قطب‌های تابع تبدیل حلقه باز سیستم یا GH هستند. ما ابتدا کانتورهای صفحه S را به صفحه $$ 1 + G H $$ نگاشت می‌کنیم. سپس برای سادگی از یک در $$ 1 + G H $$ صرف نظر می‌کنیم و کانتورها را به صفحه GH نگاشت می‌کنیم. کانتورهایی که در این مرحله به دست می‌آیند، اطلاعاتی را درباره ریشه‌هایی به دست می‌دهند که دارای قسمت حقیقی مثبت هستند. در واقع، این‌ها همان ریشه‌هایی هستند که در  صفحه سمت راست واقع شده‌اند.

قضیه کوشی (Cauchy’s Theorem)

قضیه کوشی قادر است که اطلاعاتی را درباره تعداد صفرهای مربوط به تابع $$ F ( S ) $$ فراهم کند که قسمت حقیقی مثبت دارند. در مورد بررسی پایداری یک سیستم، قضیه را باید به معادله مشخصه آن اعمال کرد که به صورت زیر نوشته می‌شود:

$$ F ( S ) = 1 + G H ( S ) = 0 \; \; \; \; \; \; \; ( 1 )  $$

در این معادله $$ F ( S ) $$ معمولا به صورت زیر بیان می‌شود:

$$ F ( s ) = \frac { K \left ( s + z _ { 1 } \right) \left( s + z _ { 2 } \right) \cdots \left( s + z _ { n } \right)}{ \left ( s + p _ { 1 } \right) \left ( s + p _ { 2 } \right) \cdots \left ( s + p _ { m } \right ) } = 0 \; \; \; \; \; \; ( 2 ) $$

حال اگر قضیه کوشی را به معادلات ۱ و ۲ اعمال کنیم، به صورت زیر خواهد بود.

اگر:

1. یک کانتور در صفحه S را نگاشت کنیم که صفرهای Z و قطب‌های P مربوط به $$ F ( S ) $$ را محاصره کرده‌اند.
2. کانتور از هیچ قطب یا صفر $$ F ( S ) $$ عبور نکند.
3. جهت تراگشتی کانتورها در صفحه S ساعت‌گرد باشد.

آن‌گاه:

کانتور متناظر (یا تصویر) در صفحه $$ F ( S ) $$، مبدا را به اندازه N = Z - P بار در جهت ساعتگرد دور می‌زند.

این قضیه را می‌توان توسط رابطه زیر خلاصه کرد:

$$ N = Z - P \; \; \; \; \; \; \; ( 3 ) $$

در این رابطه، P تعداد قطب‌های تابع $$ F ( S ) $$ و Z تعداد صفرها یا ریشه‌های $$ F (S ) $$ و N تعداد دور زدن‌های مبدا در صفحه $$ F (S ) $$ است.

نگاشت به $$ G H ( S ) $$ نسبت به نگاشت به $$ 1 + G H ( S ) = F ( S ) $$ راحت‌تر است. برای نگاشت $$ G H ( S ) $$، معادله شماره ۳ را اعمال می‌کنیم، اما این بار N را برابر با تعداد دور زدن‌های ساعت‌گرد نقطه 1- در صفحه GH فرض می‌کنیم. برای تعداد زیادی از کاربردها، $$ G H ( S ) $$ را در فرم فاکتوری زیر می‌توان نوشت:

$$ G H ( S ) = \frac { K ( s + s _ 1 ) ( s + s _ 2 ) ... } { ( s + p _ 1) ( s + p _ 2 ) ... } $$

در این رابطه $$ s _ i $$ها برابر با صفرهای تابع تبدیل حلقه باز هستند. حال با یافتن تصویر یا نگاشت در صفحه GH به جای صفحه $$ F ( S ) $$، از اضافه شدن یک به محاسبات جلوگیری می‌کنیم.

معیار پایداری نایکویست

پایداری یک سیستم را می‌توان با جست و جوی نیمه راست صفحه S برای صفرها یا ریشه‌های معادله مشخصه ($$ F ( S ) = 1 + G H ( S ) = 0 $$) تعیین کرد. اگر هیچ ریشه‌ای در سمت راست صفحه قرار نگرفته باشد، آن‌گاه می‌توان گفت که سیستم پایدار است.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

حال می‌توان رویه‌ای معین را برای جست‌و‌جوی نیمه راست صفحه و ارتباط پایداری سیستم با نمودار قطبی به دست آورد که معیار پایداری نایکویست نام دارد. محور $$ j \omega $$ مثبت در صفحه S که در نمودارهای قطبی مورد استفاده قرار می‌گیرد، به یک کانتور بسط داده می‌شود که تمام نیم صفحه راست را در بر بگیرد. کانتوری که در تصویر زیر نشان داده شده، از سه بخش تشکیل شده است.

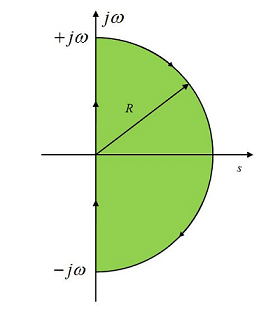
این سه بخش عبارتند از:

1. نیمه مثبت محور $$ j \omega $$
2. نیمه منفی محور $$ j \omega $$
3. نیم دایره با شعاع نامحدود R

کانتور نایکویست

به کانتور کاملی که کل نیم صفحه راست را در بر بگیرد، یک «کانتور نایکویست» (Nyquist Contour) می‌گویند. اگر بدانیم که هیچ کدام از ریشه‌های معادله مشخصه فراتر از یک منطقه خاص قرار نمی‌گیرند، آن‌گاه می‌توانیم از یک شعاع کوچک‌تر استفاده کنیم. برای نگاشت کانتور نایکویست صفحه S به صفحه GH، ما از صفحه GH استفاده می‌کنیم که برابر است با:

$$ F ( S ) - 1 = G H ( S ) $$

این تغییر در تابع نگاشت بسیار ساده است؛ زیرا ما همواره $$ G H ( S ) $$ را در فرم فاکتوری به صورت زیر می‌شناسیم:

$$ G H ( S ) = \frac { K (s + s _ 1 ) ( s + s _ 2 ) . . . } { ( s + p _ 1 ) ( s + p _ 2 ) . . . } $$

حال می‌توانیم معیار پایداری لیاپانوف را به صورت زیر بیان کنیم:

زمانی که کانتور نایکویست توسط تابع تبدیل حلقه باز $$ G H ( S ) $$ به صفحه $$ G H ( S ) $$ نگاشت شود، آن‌گاه یکی از دو حالت زیر اعمال می‌شود:

حالت اول: زمانی که هیچ کدام از قطب‌های $$ G H ( S ) $$ در نیمه راست صفحه S نباشند، سیستم کنترل فیدبک متناظر یک سیستم پایدار محسوب می‌شود اگر و فقط اگر کانتور تصویر کانتور نایکویست نقطه $$ - 1 + j 0 $$ را در صفحه $$ G H ( S ) $$ دور نزند.

حالت دوم: زمانی که تعداد قطب‌های $$ G H ( S ) $$ در سمت راست صفحه S غیر صفر باشد، سیستم کنترل فیدبک متناظر پایدار محسوب می‌شود اگر و فقط اگر کانتور تصویر کانتور نایکویست نقطه $$ - 1 + j 0 $$ را در جهت پادساعتگرد به اندازه تعداد قطب‌های $$ G H ( S ) $$ با بخش حقیقی مثبت، دور بزند.

اساس این دو حالت بر رابطه $$ N = Z - P $$ استوار است که همان معیار پایداری نایکویست است. برای حالت اول، در صورتی که $$ P = 0 $$ باشد، رابطه $$ N = Z $$ صحیح است. یعنی تعداد صفرها باید برابر با تعداد دور زدن‌ها باشد. برای یک سیستم پایدار، N باید برابر با صفر باشد. برای حالت دوم، $$ N = Z - P $$ تبدیل به $$ N = - P $$ می‌شود؛ زیرا در یک سیستم پایدار $$ Z = 0 $$ است.

مثال۱: معیار پایداری نایکویست

تابع انتقال حلقه باز یک سیستم با پیکربندی فیدبک واحد استاندارد به صورت زیر است:

$$ G ( s ) = \frac { 1 } { ( s + 1 ) ( s + 2 ) } . $$

این سیستم هیچ قطب حلقه بازی در سمت راست صفحه ندارد. مقدار K را به نحوی تعیین کنید که سیستم حلقه بسته پایدار باشد.

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

حل

ابتدا می‌خواهیم این سوال را با معیار راوث هرویتز حل کنیم. معادله مشخصه این سیستم به صورت زیر نوشته می‌شود:

$$ \begin {align*}
( s + 1 ) ( s + 2 ) + K = 0 \iff s ^ 2 + 3 s + K + 2 = 0.
\end {align*} $$

با استفاده از معیار پایداری راوث هرویتز برای یک چند جمله‌ای درجه دو، می‌توان به این نتیجه رسید که سیستم به ازای $$ K > - 2 $$ پایدار است. حال می‌خواهیم با استفاده از معیار پایداری نایکویست نیز به نتیجه مشابهی برسیم. در تصویر زیر، نمودار بود مربوط به این سیستم رسم شده است.

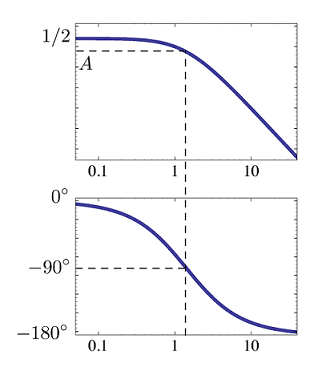
از نمودار بود می‌توان برای رسم کردن $$ \text{Im } G(j\omega) $$ بر حسب $$ \text{Re } G ( j \omega ) $$ برای $$ 0 \le \omega < \infty $$ استفاده کرد. در تصویر زیر نیمه‌ای از نمودار نایکویست این سیستم رسم شده است.

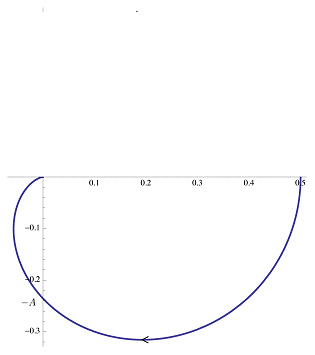
اما این نصفی از نمودار نایکویست سیستم است. با استفاده از خاصیت تقارن می‌توان نوشت:

$$ G ( - j \omega) = \overline { G ( j \omega ) }. $$

این بدین معنی است که برای به دست آوردن نیمه دیگر نمودار نایکویست، می‌توان از نیمه اول مزدوج گرفت.

$$ \left ( \text {Re } G(j\omega), \text{Im } G(j\omega)\right) \text{ for } -\infty < \omega < \infty. $$

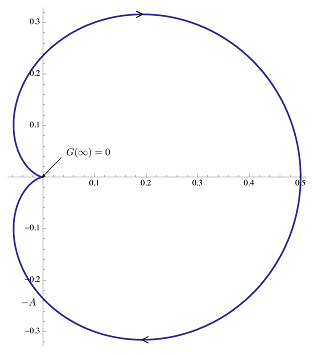
نمودار نایکویست همواره نسبت به محور حقیقی دارای تقارن است. حال از طریق اعمال معیار پایداری نایکویست داریم:

$$ \begin{align*}
&\#(\circlearrowright \text{ of $-1/K$}) \\
&= \#(\text{RHP CL poles}) - \underbrace{\#(\text{RHP OL poles})}_{=0}.
\end{align*} $$

به دلیل این که در صورت سوال ذکر شده است که سیستم هیچ قطب حلقه بازی در سمت راست صفحه ندارد، در نتیجه $$ K \in R $$ پایدار است اگر و فقط اگر:

$$ \begin{align*}
\#(\circlearrowright \text{ of $-1/K$}) = 0.
\end{align*} $$

با استفاده از این رابطه، می‌توان به نتایج زیر رسید:

• اگر $$ - \frac { 1 } K < 0 $$ یا به عبارتی $$ K > 0 $$ باشد، آن‌گاه $$ \#(\circlearrowright \text{ of $- 1 / K $ } ) = 0 $$ است.
• اگر $$ 0 < - \frac { 1 } K < 0.5 $$ باشد، آن‌گاه $$ \#(\circlearrowright \text{ of $ - 1 / K $ } ) > 0 $$ است.
• اگر $$ -\frac { 1 } K > 0.5 $$ یا به عبارتی $$ K > -2 $$ باشد، آن‌گاه $$ \#(\circlearrowright \text{ of $ - 1 / K $ } ) = 0 $$ است.

نمودار نایکویست

نمودار نایکویست که گاهی به آن نمودار قطبی نیز می‌گویند، در واقع پاسخ فرکانسی یک سیستم خطی است. به عبارت دیگر، در تابع تبدیل $$ G ( S ) $$ به جای تمام Sها، باید $$ j \omega $$ قرار دهیم. از نمودار نایکویست به عنوان ابزار اصلی معیار پایداری نایکویست استفاده می‌کنیم.

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

به منظور ترسیم نمودار نایکویست مربوط به تابع تبدیل $$ G ( j \omega ) $$ در بازه فرکانسی ۰ تا بی‌نهایت، باید چهار نقطه مهم زیر را شناسایی کنیم:

1. شروع ترسیم نمودار که در $$ \omega = 0 $$ قرار دارد.
2. پایان نمودار که در $$ \omega = \infty $$ قرار دارد.
3. محلی که نمودار از محور حقیقی عبور می‌کند یا به عبارتی $$ \text { Imaginary } ( G ( j ω ) ) = 0 $$.
4. محلی که نمودار از محور موهومی عبور می‌کند یا به عبارتی $$ \text { Real } ( G ( j ω ) ) = 0 $$.

مثال۲: ترسیم نمودار نایکویست

سیستم مرتبه اول زیر را در نظر بگیرید:

$$ G ( S ) = \frac { 1 } { 1 + s T } $$

در این رابطه T برابر با ثابت زمانی سیستم در نظر گرفته می‌شود. حال می‌خواهیم از طریق جایگذاری $$ j ω $$ به جای $$ S $$، تابع $$ G ( S ) $$ را به صورت پاسخ فرکانسی $$ G ( j ω ) $$ نمایش دهیم. در نتیجه داریم:

$$ G ( S ) = \frac { 1 } { 1 + j ω T } $$

دامنه $$ | G ( j ω ) | $$ به صورت زیر به دست می‌آید:

$$ | G ( j ω ) | = \frac { 1 } { \sqrt { 1 + ω ^ 2 T ^ 2 } } $$

فاز $$ G ( j ω ) $$ که با $$ \phi $$ نمایش داده می‌شود را نیز می‌توان به صورت زیر محاسبه کرد:

$$ \angle G ( j ω ) = - \arctan ( ω T ) $$

محل شروع نمودار نایکویست در $$ ω = 0 $$ به صورت زیر به دست می‌آید:

$$ | G ( j ω ) | = \frac { 1 } { \sqrt { 1 + 0 } } = 1 $$

$$ \angle G ( j ω ) = \phi = - \arctan ( \frac { 0 } { 1 } ) = 0 $$

به طریق مشابه اندازه و زاویه پایان نمودار نایکویست در $$ \omega = \infty $$ را نیز به دست می‌آوریم:

$$ | G ( j ω ) | = \frac { 1 } { \sqrt { 1 + \infty } } = 0 $$\\
$$ \angle G ( j ω ) = \phi = \arctan ( \frac { - \infty } { 1 } ) = - 90 ^ \circ $$

قسمت میانی نمودار که در $$ \omega = \frac { 1 } { T } $$ قرار دارد:

$$ | G ( j ω ) | = \frac { 1 } { \sqrt { 1 + 1 } } = \frac { 1 } { \sqrt { 2 }} $$\\
$$ \angle G ( j ω ) = \phi = \arctan ( \frac { - 1 } { 1 } ) = - 45 ^ \circ $$

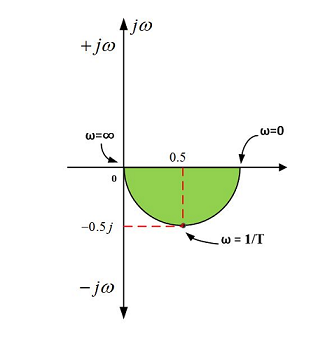
بنابراین برای یک سیستم مرتبه اول، نمودار قطبی یا نمودار نایکویست به صورت زیر ترسیم می شود:

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی کنترل
• آموزش کنترل خطی با رویکرد حل مساله
• مجموعه آموزش‌های مهندسی برق
• آموزش سیستم های کنترل خطی
• معیار پایداری راث هرویتز — به زبان ساده
• جبران ساز پیش فاز و پس فاز — از صفر تا صد
• پاسخ سیستم مرتبه دوم — از صفر تا صد

^^