مشتق ln(x+1) – به زبان ساده + مثال و حل تمرین

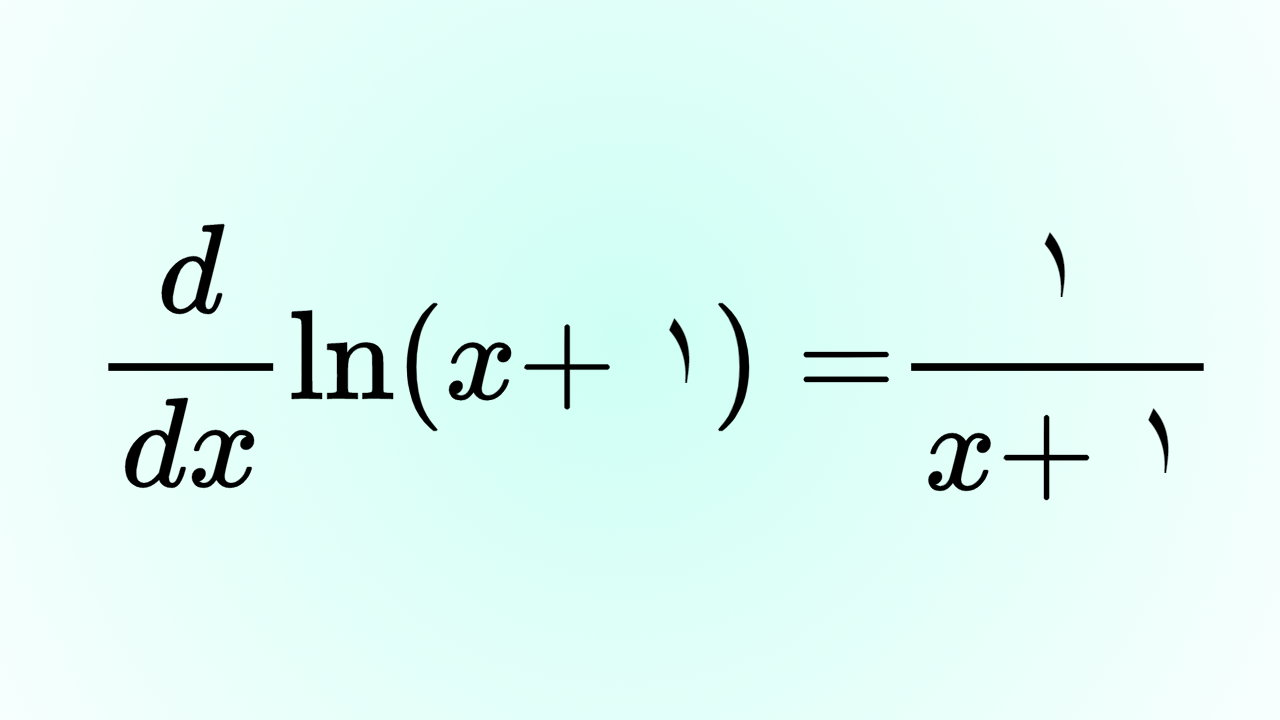
مشتق ln (x+۱) برابر با $$ \frac { ۱ } { x + ۱ } $$ است. ln، به منظور نمایش یک لگاریتم خاص مورد استفاده قرار می‌گیرد. این لگاریتم با عنوان لگاریتم طبیعی شناخته می‌شود. اگر مبنای لگاریتم را برابر با ثابت عددی e یا همان عدد اویلر (۲/۷۱۸۲۸)، قرار دهیم، لگاریتم طبیعی $$ (\log _ { ۲/۷۱۸۲۸ } ( x ) = \ln ( x )) $$ به وجود می‌آید. مشتق‌گیری از لگاریتم‌های طبیعی، قواعد مخصوص به خود را دارد. در این مقاله، روش‌های گرفتن مشتق ln (x+۱) را به همراه حل چندین مثال و تمرین متنوع آموزش می‌دهیم. در انتها نیز به اثبات فرمول مشتق ln(x+۱) می‌پردازیم.

مشتق log چیست ؟

به منظور آشنایی با نحوه محاسبه مشتق ln(x+۱)، ابتدا باید با حالت‌های مختلف مشتق‌گیری از توابع لگاریتمی، مخصوص لگاریتم طبیعی آشنا شوید. به این منظور، تابع لگاریتمی زیر را در نظر بگیرید:

$$
\log _ { a } [ f ( x ) ]
$$

مشتق تابع لگاریتمی بالا، از رابطه زیر به دست می‌آید:

$$ \frac { d } { d x } \log _ a [ f ( x ) ] = \frac { f ' ( x ) } { f ( x ) \ln ( a ) } $$

به عنوان مثال، اگر $$ f ( x ) = x $$ باشد، مشتق تابع $$ \log _ { a } ( x ) $$ برابر می‌شود با:

$$ \frac { d } { d x } \log _ a ( x ) = \frac { ۱ } { x \ln ( a ) } $$

 

مشتق ln

برای تعیین مشتق لگاریتم طبیعی (ln)، حالت‌های مختلفی به وجود می‌آید. برای شروع، تابع زیر را در نظر بگیرید:

$$ f ( x ) = \ln ( x ) $$

تابع بالا، ln(x) را نمایش می‌‌دهد. در این حالت، مشتق $$ f ( x ) $$ برابر است با:

$$
f ^ { \prime } ( x ) = \frac { d } { d x } \ln ( x )
$$

$$
= \frac { d } { d x } \log _ e ( x )
$$

$$
= \frac { ۱ } { x \ln ( e ) }
$$

$$
= \frac { ۱ } { x \log _ { e } ( e ) }
$$

$$
= \frac { ۱ } { x }
$$

اگر x دارای یک ضریب ثابت عددی مانند c بود، نتیجه مشتق ln(cx) با مشتق بالا تفاوتی نمی‌کرد. به عبارت دیگر:

$$
f ^ { \prime } ( x ) = \frac { d } { d x } \ln ( c x ) = \frac { ۱ } { x }
$$

 

تمرین ۱: تعیین مشتق ln cx

اگر c یک عدد ثابت باشد، اثبات کنید مشتق $$ \ln ( c x ) $$ با مشتق $$ \ln ( x ) $$ برابر است.

برای اثبات مشتق $$ \ln ( c x ) $$ از ویژگی ضرب در لگاریتم استفاده می‌کنیم. بر اساس این ویژگی، لگاریتم حاصل‌ضرب دو متغیر، با جمع لگاریتم‌های هر یک از آن متغیرها برابر است. به عبارت دیگر:

$$
\ln ( c x ) = \ln ( c ) + \ln ( x )
$$

مشتق جمع دو عبارت، برابر با جمع مشتق هر یک از آن عبارت‌ها است:

$$
\frac { d } { d x } \ln ( c x ) = \frac { d } { d x } \ln ( c ) + \frac { d } { d x }\ln ( x )
$$

حاصل عبارت $$ \ln ( c ) $$، یک عدد ثابت است. بنابراین، مشتق آن ($$ \frac { d } { d x } \ln ( c ) $$) برابر با صفر می‌شود:

$$
\frac { d } { d x } \ln ( c x ) = ۰ + \frac { d } { d x }\ln ( x )
$$

$$
\frac { d } { d x } \ln ( c x ) = \frac { d } { d x }\ln ( x )
$$

در نتیجه، مشتق $$ \ln ( c x ) $$ با مشتق $$ \ln ( x ) $$ برابری می‌کند.

 

مشتق ln (x+۱)

به منظور تعیین مشتق ln (x+۱)، به سراغ حالت کلی مشتق‌گیری از لگاریتم طبیعی می‌رویم. فرم کلی تابع لگاریتم طبیعی به صورت زیر نوشته می‌شود:

$$ f ( x ) = \ln [ g ( x ) ] $$

عبارت داخل لگاریتم ($$ g ( x ) $$)، تابعی از x است. در این حالت، مشتق ln از رابطه کلی زیر به دست می‌‌آید:

$$ f ' ( x ) = \frac { g ' ( x ) } { g ( x ) } $$

تا زمانی که $$ g ( x ) $$ برابر با صفر نبوده و امکان مشتق‌گیری از آن وجود داشته باشد، $$ f ' ( x ) $$ دارای جواب موجه خواهد بود. اکنون، لگاریتم طبیعی ln (x+۱) را در نظر بگیرید. عبارت داخل این لگاریتم ($$ x + ۱ $$)، تابعی از متغیر x است. این عبارت را برابر با $$ g ( x ) $$ قرار می‌دهیم:

$$
f ( x ) = \ln ( x + ۱ )
$$

$$
g ( x ) = x + ۱
$$

مطابق با رابطه کلی مشتق ln داریم:

$$ f ' ( x ) = \frac { g ' ( x ) } { g ( x ) } $$

به این ترتیب، برای به دست آوردن مشتق ln(x+۱)، باید مشتق $$ g ( x ) $$ را به دست بیاوریم:

$$
g ' ( x ) = \frac { d } { d x } g ( x )
$$

$$
= \frac { d } { d x } ( x + ۱ )
$$

$$
= \frac { d } { d x } x + \frac { d } { d x } ۱
$$

$$
= ۱ + ۰
$$

$$
g ' ( x ) = ۱
$$

اکنون، $$ g ( x ) = x + ۱ $$ و $$ g ' ( x ) = ۱ $$ را درون رابطه مشتق ln (x+۱) قرار می‌دهیم:

$$ f ' ( x ) = \frac { ۱ } { x + ۱ } $$

نکته: یکی از اشتباهات رایج بین دانش‌آموزان در هنگام مواجه با ln (x+۱) این است که تصور می‌کنند می‌توانند آن را تجزیه کرده و به شکل حاصل‌جمع دو عبارت لگاریتمی ($$\ln ( x ) + \ln ( ۱ ) $$) دربیاورند. به خطر داشته باشید که این ویژگی در اینجا کاربرد ندارد و برای لگاریتم ضرب دو عبارت قابل اجرا است.

مثال ۱: محاسبه مشتق ln (x+c)

اگر c، یک ثابت عددی باشد، نسبت مشتق ln (x+c) به مشتق ln(x+۱) را به دست بیاورید.

تابع ln (x+c) شباهت زیادی به تابع ln (x+۱) دارد. البته در این جا، به جای عدد ۱، از ثابت عددی c استفاده شده است. برای به دست مشتق ln (x+c)، از فرمول کلی مشتق ln استفاده می‌کنیم:

$$ f ' ( x ) = \frac { g ' ( x ) } { g ( x ) } $$

در فرمول بالا، داریم:

$$
g ( x ) = x + c
$$

به دلیل ثابت بودن c، خواهیم داشت:

$$
g ' ( x ) = ۱
$$

$$ g ( x ) $$ و $$ g ' ( x ) $$ را در رابطه مشتق قرار می‌دهیم:

$$ f ' ( x ) = \frac { ۱ } { x + c } $$

می‌دانیم که مشتق ln (x+۱) برابر است با:

$$
F ' ( x ) = \frac { ۱ } { x + ۱ }
$$

در نتیجه، نسبت مشتق ln (x+c) به مشتق ln(x+۱) برابر خواهد بود با:

$$
\frac { f ' ( x ) } { F ' ( x ) } = \frac { \frac { ۱ } { x + c } } { \frac { ۱ } { x + ۱ } } = \frac { x + ۱ } { x + c }
$$

مثال ۲: محاسبه مشتق ln (۲x+۵)

مشتق تابع مشتق ln (۲x+۵) را تعیین کنید.

برای تعیین مشتق ln (۲x+۵)، از فرمول کلی مشتق ln استفاده می‌کنیم:

$$ f ' ( x ) = \frac { g ' ( x ) } { g ( x ) } $$

برای این مثال، داریم:

$$
g ( x ) = ۲x + ۵
$$

مشتق این عبارت برابر است با:

$$
g ' ( x ) = ۲
$$

با جایگذاری $$ g ( x ) $$ و $$ g ' ( x ) $$ در رابطه مشتق، به جواب زیر می‌رسیم:

$$ f ' ( x ) = \frac { ۲ } { ۲x + ۵ } $$

مثال ۳: محاسبه مشتق ln (x^۲+x)

مشتق ln (x^۲+x) را با کمک مشتق ln (x+۱) به دست بیاورید.

برای محاسبه مشتق ln (x۲+x)، دو روش وجود دارد. روش اول، استفاده از فرمول کلی مشتق ln است. روش دوم، بازنویسی عبارت $$ \ln ( x ^ ۲ + x ) $$ به صورت $$ x ( x + ۱) $$ و استفاده از خصوصیات لگاریتم است. بر اساس صورت سوال، روش دوم را در پیش می‌گیریم. به این ترتیب، داریم:

$$
f ( x ) = \ln ( x ^ ۲ + x ) = \ln [ x ( x + ۱ ) ]
$$

با استفاده از قانون ضرب در لگاریتم، می‌توانیم عبارت بالا را به صورت زیر باز کنیم:

$$
f ( x ) = \ln ( x ) + \ln ( x + ۱ )
$$

مشتق تابع بالا برابر است با:

$$
f ' ( x ) = \frac { d } { d x } \ln ( x ) + \frac { d } { d x } \ln ( x + ۱ )
$$

می‌دانیم که:

$$
\frac { d } { d x } \ln ( x ) = \frac { ۱ } { x }
$$

و

$$
\frac { d } { d x } \ln ( x + ۱ ) = \frac { ۱ } { x + ۱ }
$$

در نتیجه:

$$
f ' ( x ) = \frac { ۱ } { x } + \frac { ۱ } { x + ۱ }
$$

$$
f ' ( x ) = \frac { x + ۱ + x } { x ( x + ۱ ) }
$$

$$
f ' ( x ) = \frac { ۲ x + ۱ } { x ^ ۲ + x }
$$

اثبات مشتق ln(x+۱)

اثبات مشتق ln (x+۱) با استفاده از قواعد مشتق زنجیره‌ای انجام می‌گیرد. در مطلب «مشتق ln – به زبان ساده + مثال و حل تمرین»، با استفاده از قضیه حد و پیوستگی اثبات کردیم که اگر $$ f ( x ) = \ln ( x ) $$ باشد، مشتق آن برابر با عبارت زیر می‌شود:

$$
f ' ( x ) = \lim _ { \Delta x \rightarrow ۰ } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } = \frac { ۱ } { x }
$$

فرم کلی تابع ln (x+۱)، به صورت $$ \ln [ f ( x ) ] $$ است. برای اثبات مشتق $$ \ln [ f ( x ) ] $$، از قاعده مشتق زنجیره‌ای استفاده می‌کنیم. بر اساس این قاعده، تابع بیرونی را برابر با $$ g ( x ) $$ در نظر می‌گیریم:

$$ g ( x ) = \ln ( x ) $$

تابع درونی را نیز برابر با $$ h ( x ) $$ قرار می‌دهیم:

$$ h ( x ) = f ( x ) $$

به این ترتیب داریم:

$$ \ln [ f ( x ) ] = g [ h ( x ) ] $$

بر اساس قواعد مشتق زنجیره‌ای، خواهیم داشت:

$$
\frac { d } { d x } g [ h ( x ) ] = g ' [ h ( x ) ] . h ' ( x )
$$

اکنون، بر اساس دانسته‌های قبلی، عبارت‌های سمت راست را به دست می‌آوریم:

$$
g ' ( x ) = \frac { d } { d x } \ln ( x ) = \frac { ۱ } { x }
$$

$$
\downarrow
$$

$$
g ' [ h ( x ) ] = \frac { ۱ } { h ( x ) }= \frac { ۱ } { f ( x ) }
$$

و

$$
h ' ( x ) = f ' ( x )
$$

در نتیجه:

$$
\frac { d } { d x } g [ h ( x ) ] = \frac { ۱ } { f ( x ) } f ' ( x )
$$

$$
\frac { d } { d x } \ln [ f ( x ) ] = \frac { f ' ( x ) } { f ( x ) }
$$

به این ترتیب، اگر $$ f ( x ) = x + ۱ $$ در نظر بگیریم، خواهیم داشت:

$$
\frac { d } { d x } \ln ( x + ۱ ) = \frac { \frac { d } { d x } ( x + ۱ ) } { ( x + ۱ ) }
$$

$$
\frac { d } { d x } \ln ( x + ۱ ) = \frac { ۱ } { ( x + ۱ ) }
$$

مشتق معکوس ln (x+۱)

تابع معکوس ln (x+۱) از رابطه زیر به دست می‌آید:

$$
f ( x ) = \ln ( x + ۱ )
$$

به جای $$ f ( x ) $$، متغیری مانند y را در نظر می‌گیریم:

$$
y = \ln ( x + ۱ )
$$

برای به دست آوردن معکوس تابع، جای x و y را عوض می‌کنیم:

$$
x = \ln ( y + ۱ )
$$

سپس، تابع را بر حسب y بازنویسی می‌کنیم. به این منظور، عبارت‌های دو طرف رابطه را به عنوان توان e در نظر می‌گیریم:

$$
e ^ x = e ^ { \ln ( y + ۱ ) }
$$

به این ترتیب داریم:

$$
e ^ x = y + ۱
$$

$$
y = e ^ x - ۱
$$

در نتیجه، معکوس تابع $$ f ( x ) $$ به دست می‌آید:

$$
f ( x ) ^ { - ۱ } = e ^ x - ۱
$$

تابع بالا، یک تابع نمایی است. مشتق e، به صورت زیر محاسبه می‌شود:

$$ \frac { d } { dx } e ^ { x } = e ^ x $$

 

به این ترتیب، مشتق معکوس ln (x+۱) برابر است با:

$$
\frac { d } { dx } ( e ^ x - ۱ ) = \frac { d } { dx } e ^ x - \frac { d } { dx } ۱
$$

$$
\frac { d } { dx } ( e ^ x - ۱ ) = e ^ x - ۰
$$

$$
\frac { d } { dx } ( e ^ x - ۱ ) = e ^ x
$$

در نتیجه، مشتق معکوس ln (x+۱) برابر با e^x است.

سوالات متداول در رابطه با مشتق ln (x+۱)

در این بخش، به برخی از سوالات پرتکرار در رابطه مشتق ln(x+۱) به صورت خلاصه پاسخ می‌دهیم.

ln (x+۱) چه نوع تابعی است ؟

ln (x+۱)، یک تابع لگاریتمی (لگاریتم طبیعی) است.

فرم کلی تابع ln (x+۱) چگونه است ؟

فرم کلی تابع ln (x+۱)، به صورت f(x)=ln[g(x)] است.

فرمول مشتق ln (x+۱) چیست ؟

فرمول مشتق تابع f(x)=ln (x+۱) مطابق با فرم کلی آن و به صورت f(x)=g'(x)/g(x) نوشته می‌شود.

مشتق ln(x+۱) چیست ؟

مشتق ln (x+۱) برابر با کسر (x+۱)/۱ است.

معکوس ln (x+۱) چیست ؟

معکوس ln (x+۱) برابر با e^x-۱ است.

مشتق معکوس ln (x+۱) چیست ؟

مشتق معکوس ln (x+۱) برابر با e^x است.