مرتبه اجرایی در ساختمان داده — به زبان ساده، رایگان و کامل
پیچیدگی زمانی و مرتبه اجرایی در ساختمان داده و طراحی الگوریتم از مباحث پایه و مهم در علوم کامپیوتر به حساب میآیند. دو مفهوم «پیچیدگی زمانی» و «مرتبه اجرایی» هر دو به محاسبه میزان افت عملکرد یک تابع یا الگوریتم در ازای رشد اندازه ورودی مربوط میشوند. پیچیدگی زمانی به انگلیسی «Time Complexity» خطاب میشود و گاهی به آن «پیچیدگی اجرایی» هم میگویند. در این مطلب سعی شده است تا حد امکان به طور جامع به آموزش مرتبه اجرایی در ساختمان داده پرداخته شود. همچنین برای درک بهتر، مثالها و نمونه سوالهایی هم برای اکثر بخشهای این نوشته ارائه شدهاند. همچنین در این نوشتار به مرتبه اجرایی حلقه For و While، مرتبه اجرایی توابع بازگشتی، مرتبه اجرایی فاکتوریل و سایر موارد مهم پیرامون مبحث مرتبه اجرایی در ساختمان داده پرداخته شده است.
مرتبه اجرایی در ساختمان داده چیست ؟
در برنامه نویسی برای پیادهسازی و ایجاد برنامههای نرم افزاری در اکثر مواقع الگوریتمهای مختلفی وجود دارند که کار یکسانی انجام میدهند؛ اما هر یک از این الگوریتمها زمان اجرا و سرعت متفاوتی دارند. بنابراین، در صورتی که چند الگوریتم برای پیادهسازی یک برنامه قابل استفاده باشد، لازم است ملاکی معتبر برای مقایسه آنها وجود داشته باشد تا بتوان الگوریتم بهینه را مشخص کرد. یک راه این است که زمان اجرای الگوریتم ملاک قرار داده شود.
اما این سوال بوجود میآید که آیا زمان اجرا معیار مناسبی برای این منظور است؟ خیر، زیرا توان سختافزاری هم در زمان اجرا تاثیر دارد و برنامه در کامپیوترهای مختلف زمان اجرای متفاوتی خواهد داشت. همچنین، اگر همزمان با برنامه مربوطه، برنامههای دیگری هم روی سیستم در حال اجرا باشند، آنگاه منابع سختافزاری بین برنامهها تقسیم میشود و قدرت پردازشی کمتری در اختیار برنامه مورد نظر قرار خواهد گرفت؛ این مسئله هم باعث میشود که سنجش زمان اجرای برنامه با استفاده از الگوریتمی خاص، ملاک مناسبی برای تعیین میزان عملکرد و کارایی آن الگوریتم نباشد. بنابراین لازم است معیار بهتری برای این مقصود استفاده شود.
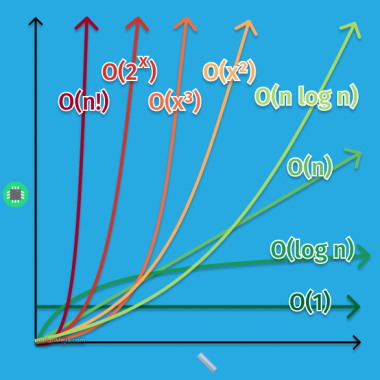
سنجش میزان رشد زمان اجرای برنامه به ازای اندازههای متفاوت ورودی میتواند انتخاب مناسبی برای مشخص کردن سطح عملکرد و کارایی یک الگوریتم باشد. به عنوان مثالی ساده اگر تابعی وجود داشته باشد که آرایهای را در ورودی دریافت کند و مجموع مقادیر عناصر آن آرایه را خروجی بدهد، با افزایش تعداد عناصر آرایه، اندازه و حجم ورودی تابع افزایش پیدا میکند.
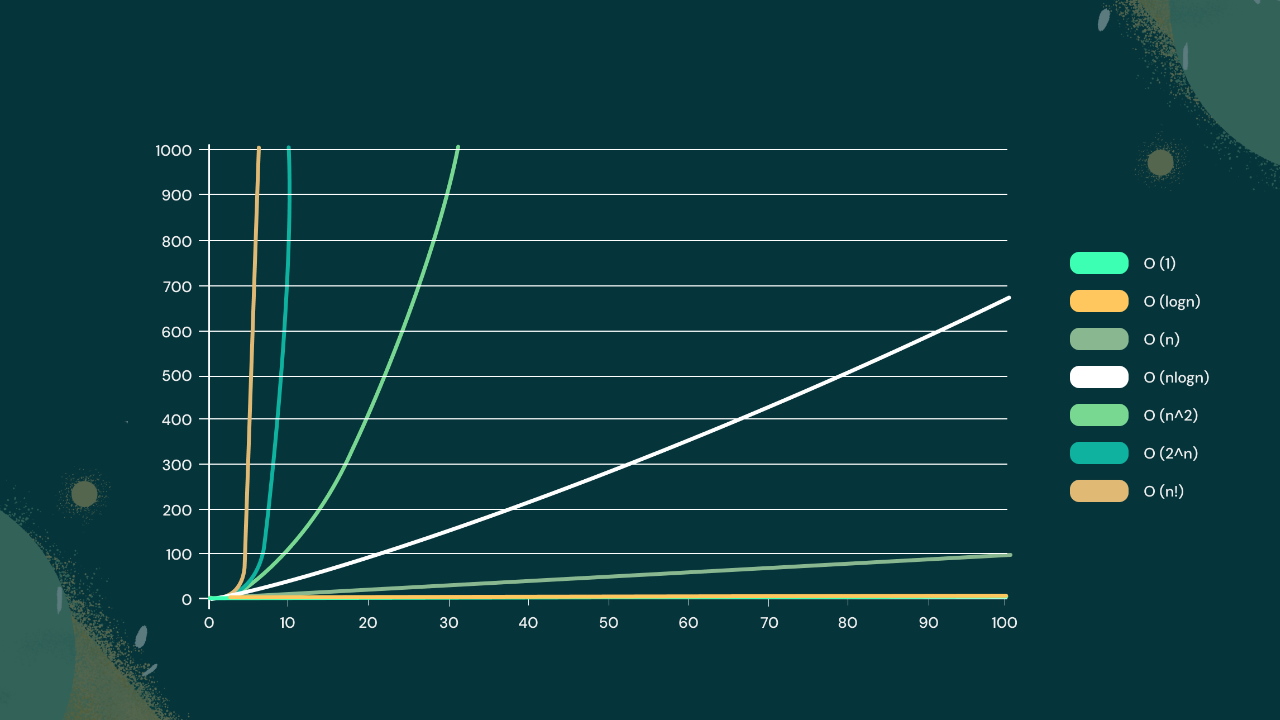
میتوان میزان رشد زمان اجرای این برنامه را نسبت به افزایش اندازه ورودی روی نمودار نشان داد؛ بهگونهای که محور x نشان دهنده اندازه ورودی و محور y هم زمان اجرا به ازای هر ورودی باشد. در این صورت، مشخص میشود که میزان رشد زمان اجرا نسبت به افزایش اندازه ورودی دارای نظم خاصی است و از تابع مشخصی تبعیت میکند. این نمودار و تابع ممکن است ثابت، خطی یا سهمی باشد. به این تابع، پیچیدگی زمانی میگویند.
مرتبه اجرایی در ساختمان داده روش و رویکردی ریاضیاتی برای نمایش نسبت رشد اندازه ورودی به رشد زمان اجرا یا همان تابع و نمودار بدست آمده در این خصوص است. برای نمایش مرتبه اجرایی در ساختمان داده از «نمادها» (Notation) استفاده میشود. یکی از رایجترین نمادها برای مرتبه اجرایی در ساختمان داده، «نماد O بزرگ» (Big O Notation) است که در ادامه این مقاله به آموزش آن و ۲ نماد رایج دیگر پرداخته میشود. مثلاً مرتبه اجرایی خطی در ساختمان داده را میتوان به صورت $$ O(n)$$ نشان داد. در تصویر فوق، مرتبه اجرایی یا همان پیچیدگیهای اجرایی مختلف در ساختمان داده با نماد O بزرگ نمایش داده شده است.
پیچیدگی اجرایی در ساختمان داده چیست ؟
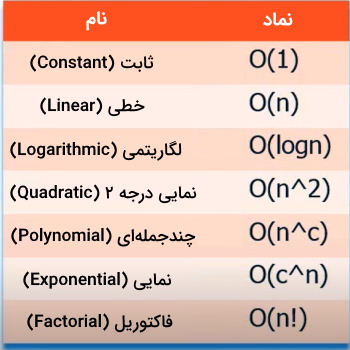
پیچیدگی یک الگوریتم به تابعی گفته میشود که خروجی آن، مدت زمان اجرای الگوریتم و ورودی آن، اندازه دادههای ورودی است. در ساختمان داده معمولاً تعداد دادههای ورودی با n نمایش داده میشود. در واقع تابع پیچیدگی اجرایی، مدت زمان اجرای به کار گرفته شده توسط الگوریتم را برحسب تعداد دادههای ورودی n اندازهگیری میکند. در جدول زیر برخی از انواع رایج پیچیدگی اجرایی آمده است:
مفهوم T(n) در ارتباط با نماد O بزرگ O(n) چیست؟
در بحث الگوریتمها، استفاده معمول از نماد $$ T$$ برای نمایش پیچیدگی زمانی الگوریتم به کار گرفته میشود. $$ T$$ یک تابع به حساب میآید. ورودی این تابع اندازه ورودی الگوریتم و خروجی آن زمان اجرای الگوریتم (در بدترین حالت) برای آن ورودی با اندازه مربوطه است. بنابراین، $$T(n)$$ یک عدد است؛ عددی که به وسیله تابع $$ T$$ در زمان دریافت عدد $$n$$ بازگردانده میشود. این عدد، زمان اجرای الگوریتم برای ورودی با اندازه $$n$$ است.
حرف $$O$$ در $$O(n)$$ یک تابع نیست. این در واقع همان «نماد O بزرگ» یا «Big O Notation» است. در واقع، $$O(n)$$ نمادی از کلاس و دسته تمام توابعی به حساب میآید که (بهطور مجانبی) حداکثر با سرعت یکسانی با تابع خطی $$ f(n) = n$$ رشد میکند.
نماد O بزرگ روشی مطلوب برای بحث راجع به کرانهای بالا محسوب میشود. برای مثال، میتوان گفت پیچیدگی زمانی یا مرتبه اجرایی یک الگوریتم مثلاً $$O(n^2)$$ است. البته بهطور رسمی و به زبان ریاضی اینگونه نوشته میشود:
$$ T \in O(n^2)$$
رابطه فوق بیان میدارد که زمان اجرای الگوریتم در بدترین حالت اندازه ورودی، به صورت نمایی درجه دوم است. گاهی مشاهده میشود که از هر دو نماد T و O در یک رابطه استفاده شده است. برای مثال، پیچیدگی زمانی یا همان مرتبه اجرایی «مرتبسازی ادغامی» (Merge Sort) اغلب به وسیله رابطه بازگشتی (Recurrence Relation) زیر توصیف میشود:
$$ T (n)= 2 T({n \over 2}) + O(n)$$
مفهوم رابطه فوق این است که برای هر $$n$$، زمان $$T(n)$$ مورد نیاز برای مرتبسازی $$n$$ عنصر را میتوان به وسیله محاسبه زمان $$T({n \over 2})$$ مورد نیاز برای مرتبسازی تعداد $${n \over 2}$$ عنصر، ضرب این زمان در ۲ و اضافه کردن «چیزی بیشتر» بدست آورد. آن چیزی بیشتر باید حداکثر در $$n$$ خطی باشد؛ یعنی از مرتبه $$O(n)$$ باشد.
مرتبه اجرایی در ساختمان داده توابع چند جمله ای
فرض میشود تابعی چند جملهای با نام $$f(n)$$ به صورت زیر وجود دارد:
$$f(n) = n^m + n^{m-1}+ ... + n^2 + n +c$$
آنگاه مرتبه اجرایی در ساختمان داده این تابع چند جملهای به صورت زیر خواهد بود:
$$f(n) = O(n^m)$$
یعنی داریم:
$$f(n) = n^m + n^{m-1}+ ... + n^2 + n +c =>\; f(n) = O(n^m)$$
به طور کلی مرتبه اجرایی در ساختمان داده توابعی چندجملهای با ساختاری که در رابطه فوق نشان داده شد، برابر با $$ O(n^m) $$ است. در واقع این میزان مطابق با بزرگترین جملهای است که در آن چندجملهای وجود دارد. به بیان دیگر، جمله اثرگذار در یک چندجملهای یا اثرگذارترین جمله به عنوان مرتبه اجرایی در ساختمان داده چندجملهای در نظر گرفته میشود.
اگر هر یک از جملههای چندجملهای دارای ضریب هم باشند، آنگاه هیچگونه تاثیری در مرتبه اجرایی به وجود نخواهد آمد. برای درک بهتر مرتبه اجرایی در توابع چندجملهای در ادامه مثالی ارائه شده است.
مثال مرتبه اجرایی در ساختمان داده توابع چند جمله ای
در این مثال فرض میشود $$ f(n) $$ به صورت زیر باشد:
$$f(n) = 6n^2 - 4n+5$$
اثرگذارترین جمله در چندجملهای فوق، جمله $$ 6n^2$$ است، بنابراین، مرتبه اجرایی در ساختمان داده چندجملهای در این مثال برابر با $$ O(n^2) $$ خواهد بود. مرتبه اجرایی در ساختمان داده با حرف O برگرفته شده از کلمه «Ordnung» به معنی «مرتبه تقریبی» (Order of Approximation) نشان داده میشود. Order به معنی مرتبه است. وقتی میگوییم Order یک تابع $$n^2$$ است، یعنی مرتبه تقریبی آن تابع متعلق به پیچیدگی از جنس تابع $$ n^2$$ است و آن را با $$ O(n^2)$$ نشان میدهند.
ضرایب جملهها در توابع چندجملهای اثری در مرتبه اجرایی ندارند. مثلاً در تابع بالا اگر ضریب جمله $$ 6n^2$$ به جای عدد $$6$$، عدد ۱۰ یا حتی ۱۰۰ هزار باشد، تاثیری در مرتبه اجرایی ساختمان داده نخواهد داشت. همچنین، سایر ضرایب تابع چندجملهای در این مثال، یعنی عددهای ۴ و ۵ هم هیچ تاثیری در Order آن ندارند.
معرفی فیلم های آموزش ساختمان داده و طراحی الگوریتم

در پلتفرم فرادرس، مجموعه آموزشی اختصاصی برای ساختمان داده و طراحی الگوریتم ارائه شده است. در این صفحه تمامی دورههای آموزشی مرتبط با ساختمان داده و طراحی الگوریتم گردآوری شدهاند. ساختمان داده و الگوریتمها از مباحث بسیار مهم و پایه در رشته علوم کامپیوتر به حساب میآید. یادگیری این مفاهیم پیشنیاز بسیار مهمی برای آن دسته از افرادی محسوب میشود که قصد دارند در حوزه علوم کامپیوتر و برنامه نویسی فعالیت کنند. به ویژه در حوزه هوش مصنوعی و یادگیری ماشین هم ساختمان داده و الگوریتمها پیشنیازی بسیار مهم و ضروری به شمار میرود. در تصویر فوق تنها برخی از دورههای آموزشی این مجموعه نشان داده شدهاند.
- برای شروع یادگیری ساختمان داده و طراحی الگوریتم + اینجا کلیک کنید.
مقایسه رایج ترین مرتبه های اجرایی در ساختمان داده
به طور کلی میتوان بزرگی مرتبههای اجرایی رایج و شناختهشده را به صورت زیر نشان داد:
O(1) < O(lg n) < O(n) < O(n lg n) < O(n2) < O(2n) < O(n!)
لازم به توضیح است که منظور از $$ O( \lg n) $$ در واقع لگاریتم $$ n $$ در پایه ۲ یعنی $$ log_{2}^{n}$$ است. مرتبههای اجرایی دیگری هم وجود دارند که میتوان در بین موارد فوق جای داد و در رابطه فوق تنها مرتبههای اجرایی رایجی آمدهاند که بیشتر در ساختمان دادهها و الگوریتمها با آنها سر و کار داریم.
میتوان الگوریتمی یکسان را با مرتبههای اجرایی مختلفی نوشت و ایجاد کرد. مثلاً ممکن است فردی الگوریتم مرتبسازی را با مرتبه اجرایی $$ O(n \lg n) $$ بنویسد و فردی دیگر همین الگوریتم را با مرتبه اجرایی متفاوتی مثلاً با مرتبه $$O(n^2) $$ بنویسد.
در چنین شرایطی الگوریتمی بهتر است که مرتبه اجرایی آن کوچکتر، یعنی در این مثال از مرتبه $$ O(n \lg n) $$ باشد.
وقتی مرتبه اجرایی یک الگوریتم از مرتبه اجرایی الگوریتم دیگر کمتر باشد، یعنی سرعت اجرای آن بهتر و بالاتر است. این حقیقت را میتوان با مقداردهی هر یک از مرتبههای اجرایی مربوطه به اثبات رساند.
یعنی برای مقایسه ۲ مرتبه اجرایی مختلف، میتوان به جای متغیر $$n$$ در هر دو رابطه عدد ثابتی را قرار داد و با بدست آوردن مقدار حاصل شده، هر کدام که عدد بزرگتری باشد به معنای آن است که مرتبه اجرایی بزرگتری دارد و بنابراین سرعت اجرای آن کمتر است.
مثالی برای مقایسه رایج ترین مرتبه های اجرایی در ساختمان داده
برای مثال در خصوص الگوریتم جستجو در مبحث ساختمان داده، الگوریتمی به نام «جستجوی دودویی» (Binary Search) وجود دارد که مرتبه اجرایی آن $$ O( \lg n) $$ است. از طرف دیگر، الگوریتم جستجوی دیگری هم به نام «جستجوی خطی» (Linear Search) وجود دارد که مرتبه اجرایی آن $$ n $$ است که آن را به صورت $$ O(n) $$ نشان میدهند.
در این مثال الگوریتم جستجویی که مرتبه اجرایی آن کمتر است، جستجوی سریعتری به حساب میآید. همیشه باید سعی کرد الگوریتمی به کار برده شود که مرتبه اجرایی آن کمتر و ضعیفتر است.
نمادهای رایج برای نمایش پیچیدگی اجرایی در ساختمان داده و الگوریتم ها
در این بخش به معرفی نمادهای رایج برای نمایش پیچیدگی اجرایی در ساختمان داده و الگوریتمها پرداخته شده است. این نمادهای رایج در ادامه ابتدا فهرست میشوند و سپس توضیحات لازم برای هر یک ارائه خواهد شد.
- نماد $$O $$ (O بزرگ) در پیچیدگی اجرایی (Big O Notation)
- نماد $$ \Omega $$ (امگا بزرگ) برای مرتبه اجرایی در ساختمان داده
- نوتیشن (Notation) یا همان نماد $$ \theta $$ (تتا)
نماد O بزرگ در مرتبه اجرایی ساختمان داده و الگوریتم ها
از این نماد در اصل به صورت $$ f(n) \in O(g(n)) $$ استفاده میشود و مفهومش این است که $$ f(n)$$ به پیچیدگی اجرایی O بزرگ تابع $$ g(n)$$ تعلق دارد. در واقع اگر فرض شود پیچیدگی، تابع $$ g(n)$$ باشد، آنگاه $$ O(g(n))$$ به مجموعهای از توابع اشاره دارد که برای آنها ثابتهای $$ C $$ و $$ n_0 $$ وجود دارند و برای همهی $$ n \geq n_0 $$، رابطه $$ f(n) \le cg(n) $$ برقرار است.
یعنی اگر رابطه $$ f(n) \le cg(n) $$ برقرار باشد، آنگاه $$ f(n)$$ به ازای $$ n \geq n_0 $$، پیچیدگی اجرایی O بزرگ تابع $$ g(n)$$ تعلق دارد. به بیان سادهتر، وقتی از نماد O بزرگ استفاده میشود که $$ f(n)$$ از $$ g(n)$$ کوچکتر باشد. برای درک بهتر این مسئله در ادامه مثالی در قالب پرسش ارائه شده است.
مثال ۱ نماد O بزرگ در مرتبه اجرایی — نشان دهید: $$ n^2 + 10n \in O(n^2) $$
در اینجا $$ g(n) = n^2 $$ و $$ f(n) = n^2 + 10n $$ را داریم. طبق تعریفی که پیشتر در این بخش ارائه شد، باید نشان داده شود که رابطه زیر برقرار است:
$$ n^2 + 10n \leq cn^2 $$
بنابراین اگر بتوان نشان داد که به ازای مقدار خاصی برای ضریب $$ c $$ رابطه فوق برقرار است، آنگاه مسئله حل خواهد شد و درستی عبارت $$ n^2 + 10n \in O(n^2) $$ به اثبات خواهد رسید.
اگر مقدار ضریب $$ c $$ برابر با عدد یک باشد، آنگاه رابطه فوق برقرار نخواهد بود؛ زیرا $$ n^2 + 10n \nleq cn^2 $$ است.
اما اگر به ضریب c مقدار ۲ را اختصاص دهیم، آنگاه رابطه برقرار خواهد شد:
$$ n^2 + 10n \leq 2n^2 $$
بنابراین میتوان مقدار ۲ را برای ضریب c انتخاب کرد. در تعریف مرتبه اجرایی در ساختمان داده علاوهبر c، ضریب دیگری هم به نام $$ n_0 $$ وجود داشت که لازم است برای اثبات از مرتبه $$ n^2 $$ بودن چندجملهای مربوطه در این مسئله، مقدار آن را هم تعیین کنیم.
حالا برای پیدا کردن مقدار $$ n_0$$ در این تعریف، لازم است دو تابع $$ f(n) $$ و $$ g(n) $$ را با هم قطع بدهیم یا به بیان سادهتر، مساوی هم قرار بدهیم:
$$ n^2 + 10n = 2n^2 =>\; 10n = n^2 =>\; n= 10 $$
برای درک بهتر اینکه چرا ۲ تابع با هم قطع داده میشوند، در ادامه تصویری از نمودار ۲ تابع ارائه شده است و پس از این تصویر نیز توضیحات لازم ارائه شدهاند.
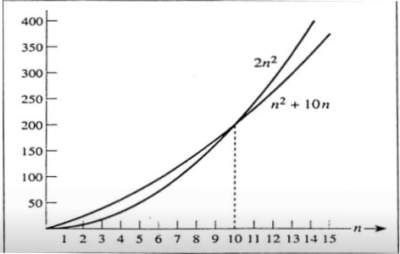
در نمودار فوق ملاحظه میشود که تا قبل از نقطه $$ n = 10 $$ تابع $$ n^2 + 10n $$ از تابع $$ 2n^2$$ بزرگتر است و نمودار آن بالای نمودار $$ g(n) $$ قرار گرفته است. بنابراین رابطه $$ f(n) \le cg(n) $$ در این ناحیه برقرار نیست؛ یعنی تا قبل از نقطه $$ n = 10 $$ تابع چندجملهای $$ f(n)$$ در این مثال متعلق به مرتبه اجرایی $$ O(n^2$$ نیست. اما پس از آن، ۲ نمودار یکدیگر را قطع کردهاند و تا بینهایت، تابع $$ 2n^2$$ از $$ n^2 + 10n $$ بزرگتر خواهد بود و بنابراین میتوان گفت $$ n^2 + 10n \in O(n^2) $$ برقرار است.
مثال ۲ نماد O بزرگ در مرتبه اجرایی — نشان دهید: $$ {n(n-1) \over 2} \in O(n^2) $$
باز هم مثل سوال (مثال) قبل، باید نشان دهیم که رابطه زیر برای همه $$ n \geq n_0 $$ برقرار است:
$$ {n(n-1) \over 2} \leq cn^2 $$
حالا دوباره باید مقداری را برای ضریب c پیدا کنیم که به ازای آن عبارت فوق برقرار باشد. اگر برای ضریب c مقدار $$ 1 \over 2 $$ انتخاب شود، آنگاه رابطه فوق برقرار خواهد بود:
$$ {n(n-1) \over 2} \leq {n^2 \over 2} $$
حالا اگر دو تابع فوق را برابر با یکدیگر قرار بدهیم یا به اصطلاح آنها را با هم قطع دهیم، مقدار $$ n $$ برابر با صفر خواهد شد و مشخص میشود که نمودارهای این ۲ تابع یکدیگر را در نقطه $$ n=0$$ قطع خواهند کرد:
$$ {n(n-1) \over 2}= {n^2 \over 2} =>\; n =0$$
با پیدا کردن مقادیر مناسب برای $$ c $$ و $$ n_0 $$ و برقرار شدن رابطه $$ {n(n-1) \over 2} \leq cn^2 $$ مشخص میشود که $$ n^2 + 10n \in O(n^2) $$ است.
مثالی برای درک بهتر نماد O بزرگ در مرتبه اجرایی ساختمان داده و الگوریتم ها
به عنوان مثال در این بخش تصویری ارائه شده است که در آن طبقهبندی و کلاسهای مربوط به تفاوت مرتبههای اجرایی مختلف در آن به نمایش گذاشته شده است.
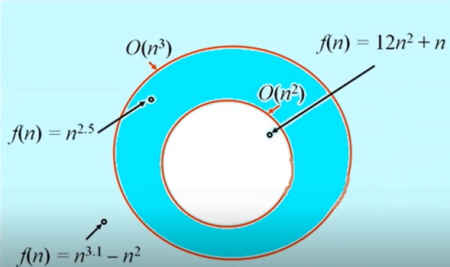
در تصویر فوق ۳ تابع $$ f(n) $$ مختلف به عنوان نمونه ملاحظه میشوند. دایره بزرگتر مرز مرتبه اجرایی $$ O(n^3)$$ به حساب میآید. یعنی هر تابعی که در محدوده داخل دایره بزرگتر قرار بگیرد، در کلاس $$ n^3 $$ قرار دارد و مرتبه اجرایی آن از $$ n^3 $$ کمتر یا مساوی با آن است. دایره کوچکتر در داخل دایره بزرگ هم محدوده $$ O(n^2)$$ را مشخص میکند و هر تابعی که در محدوده آن قرار بگیرد هم متعلق به کلاس این مرتبه اجرایی خواهد بود.
همچنین در تصویر فوق مشخص میشود که چگونه مرتبههای اجرایی همدیگر را پوشش میدهند. یعنی میتوان متوجه شد که در تابع عضو مرتبه اجرایی $$ O(n^۲)$$ متعلق به کلاس مرتبه اجرایی $$ O(n^3)$$ نیز خواهد بود.
نماد امگای بزرگ در مرتبه اجرایی ساختمان داده و الگوریتم ها
از نماد «امگای بزرگ» ($$ \Omega $$) به صورت $$ f(n) \in \Omega (g(n)) $$ استفاده میشود؛ یعنی $$ f(n)$$ به پیچیدگی اجرایی اومگای بزرگ تابع $$ g(n)$$ تعلق دارد. در صورت استفاده از نماد امگا بزرگ، به جای علامت $$\leq$$ از $$\geq$$ استفاده میشود. یعنی در این حالت رابطه $$ f(n) \ge cg(n) $$ برقرار است.
به بیان دقیقتر، اگر فرض شود تابع پیچیدگی $$ g(n)$$ است، آنگاه $$ \Omega (g(n)) $$ به مجموعهای از توابع اشاره دارد که برای آن توابع، ثابتهای $$ C $$ و $$ n_0 $$ وجود دارند، بهطوریکه برای تمام $$ n \geq n_0 $$ رابطه $$ f(n) \ge cg(n) $$ برقرار باشد. در اینجا هم به بیان ساده میتوان گفت که استفاده از نماد اومگا به معنی بزرگتر بودن ه $$ f(n)$$ از $$ g(n)$$ است. حالا در ادامه برای درک بهتر نماد امگا بزرگ ۲ مثال ارائه شده است.
مثال نماد امگای بزرگ در مرتبه اجرایی — نشان دهید: $$ {n(n-1) \over 2} \in \Omega (n^2) $$
برای اینکه بتوان نشان داد $$ n(n-1) \over 2 $$ به مرتبه اجرایی $$ \Omega (n^2)$$ تعلق دارد، باید ثابت کنیم که رابطه زیر برقرار است:
$$ {n(n-1) \over 2} \in \Omega (n^2) $$
در واقع درست مثل وقتی عمل میکنیم که میخواستیم نشان بدهیم تابع مورد نظر عضو مرتبه $$ O(n)$$ است، اما این بار به جالی علامت کوچکتر مساوی از علامت بزرگتر مساوی استفاده میکنیم. حالا همانند مثالهای قبلی، لازم است ضریب c را بیابیم. در این مثال اگر مقدار c را برابر با $$ 1 \over 4 $$ قرار بدهیم و رابطه را به صورت زیر بنویسیم، به وضوح مشخص میشود که رابطه صحیح خواهد بود:
$$ {n^2 \over 2} - {n \over 2} \ge {n^2 \over 4}$$
حالا باید دو تابع را در دو طرف رابطه با هم قطع بدهیم (با هم برابر قرار بدهیم) تا مقدار $$ n_0$$ بدست آید. بنابراین داریم:
$$ {n^2 \over 2} - {n \over 2} = {n^2 \over 4} =>\; n = 2$$
بنابراین اگر مقدار c را برابر با $$ 1 \over 4 $$ قرار دهیم، مقدار $$ n_0$$ برابر با ۲ بدست خواهد آمد. به این ترتیب میتوان گفت که رابطه صورت سوال، یعنی $$ {n(n-1) \over 2} \in \Omega (n^2) $$ برقرار و تابع مربوطه متعلق به $$ \Omega (n^2)$$ است. با رسم نمودار هم میتوان مشخص کرد که از تقطه $$ n_0 = 2 $$ تا بینهایت، نمودار تابع $$ n(n-1) \over 2$$ در بالای نمودار $$ n^2 \over 4 $$ قرار میگیرد و این یعنی مقدار آن بیشتر از $$ n^2 \over 4 $$ و رابطه صورت سوال برقرار است.
نماد تتا در پیچیدگی اجرایی ساختمان داده و الگوریتم ها
اگر $$ f(n) \in \theta (g(n)) $$ (یعنی $$ f(n)$$ متعلق به $$ \theta (g(n)) $$ باشد، آنگاه این بدان معنا خواهد بود که $$ f(n)$$ هم به $$ O(g(n))$$ و هم به $$ \Omega (g(n)) $$ تعلق دارد. یعنی اگر تابعی وجود داشته باشد که هم کمتر مساوی تابع پیچیدگی باشد و هم بزرگتر مساوی آن، اشتراک این کمتر مساوی و بزرگتر مساوی بودن به معنی مساوی بودن خواهد بود که آن را با نماد $$\theta (g(n))$$ نمایش میدهند. در اینجا هم به بیان ساده میتوان گفت وقتی از نماد تتا استفاده میشود که $$ f(n)$$ از $$ g(n)$$ با هم برابر باشند.
مثال نماد تتا در مرتبه اجرایی — نشان دهید: $$ {n(n-1) \over 2} \in \theta (n^2) $$
در مثالهای قبلی نشان داده شد که رابطههای $$ {n(n-1) \over 2} \in O(n^2) $$ و $$ {n(n-1) \over 2} \in \Omega (n^2) $$ برقرار هستند. بنابراین، طبق تعریف میتوان گفت:
$$ {n(n-1) \over 2} \in \theta (n^2) $$
بهطور کلی باید گفت که مرتبه اجرایی تتا در ساختمان داده را میتوان شبیه به رابطه برابری (مساوی) فرض کرد و چون درجه یا همان رتبه چندجملهای سمت چپ با درجه چندجملهای طرف راست رابطه برابر است، آنگاه چندجملهای مربوطه به تتای $$ n^2 $$ تعلق دارد.
مرتبه اجرایی حلقه for در ساختمان داده و برنامه نویسی
پیچیدگی زمانی یا همان مرتبه اجرایی در ساختمان داده و برنامه نویسی میتواند از هر مرتبهای مثلاُ $$ O(1)$$، $$O(n)$$ یا $$O(\log n)$$ باشد که این مسئله بستگی به شرطهای حلقه و کدهایی دارد که نوشته میشوند. بنابراین لازم است مرتبه اجرایی حلقه for در شرایط و سناریوهای مختلف بررسی شود.
سناریوی اول مرتبه اجرایی حلقه for در ساختمان داده و برنامه نویسی
برای بررسی این سناریو در ادامه مثالی ارائه شده است.
1 int sum = 0;
2 for (int x = 0; x < 10; x++) {
3 sum = sum +x;
4 }حلقه فوق هر دفعه ۱۰ بار اجرا میشود. به بیان دیگر، این حلقه For برای اجرا نیاز به زمان ثابتی دارد؛ بنابراین پیچیدگی اجرایی آن ثابت است و با $$O(1)$$ نشان داده میشود.
سناریوی دوم مرتبه اجرایی حلقه for در ساختمان داده و برنامه نویسی
برای بررسی این سناریو، لازم است به کدهای زیر توجه کنید.
1 int sum = 0;
2 for (int x = 0; x < n; x++) {
3 sum = sum +x;
4 }پیچیدگی زمانی یا همان مرتبه اجرایی این حلقه for از مرتبه $$ O(n)$$ است، زیرا تعداد تکرارها با تغییر مقدار $$n$$ متفاوت خواهد بود.
سناریوی سوم مرتبه اجرایی حلقه for در ساختمان داده و برنامه نویسی
در سناریو فرض میکنیم کدهای زیر را داریم:
1 for (int x = 1; x <= n; ) {
2 x = x * 2;
3 }در کدهای فوق لازم است توجه شود که در هر تکرار، مقدار x همانطور که در ادامه نشان داده شده است، ۲ برابر میشود تا اینکه در nامین تکرار، مقدار x با $$ 2^k $$ برابر خواهد بود.
Iteration | x
-----------------
0 | 20 // = 1
1 | 21 // = 2
2 | 22 // = 4
3 | 23 // = 8
... | ...
... | ...
n | 2k
So, we can represent it as
2k = n
Apply algorithms at both sides considering base 2
=> log 2k = log n // base 2
=> k = log ( n) .
مرتبه اجرایی حلقه for تو در تو
در ادامه مثالی از حلقه for تو در تو آمده است:
1 int sum = 0;
2 for (int x = 0; x < n; x++) {
3 for (int y = 0; y < n; y++)
4 sum = sum +x+y;
5 }حلقه for تو در تو کدهای فوق، دارای مرتبه اجرایی $$ O(n^2) $$ است؛ زیرا حلقه for بیرونی برای هر تکرار n بار اجرا خواهد شد و حلقه for داخلی هم n بار اجرا میشود. بنابراین خواهیم داشت:
$$ O(n) \times I(n) = O(n^2) $$
مرتبه اجرایی توابع بازگشتی
اغلب مرتبه اجرایی توابع بازگشتی را میتوان به وسیله فرمولهسازی و حل کردن «رابطه بازگشتی» (Recurrence Relation) محاسبه کرد.

در این بخش چند مثال و یک فرمول، یعنی «قضیه اصلی» (Master Theorem) ارائه شده است که راهحلی را برای دستهای از رابطههای بازگشتی ارائه میدهد. در زمان تجزیه و تحلیل توابع بازگشتی اغلب با این رابطههای بازگشتی سر و کار داریم. همچنین در این بخش از نشان داده شده است که چگونه آن دسته از الگوریتمهای بازگشتی را تجزیه و تحلیل کنیم که به اندازه و شکل ساختمان دادهها وابسته هستند.
مرتبه اجرایی رابطه بازگشتی چیست ؟
به عنوان مقدمه، در ادامه نشان میدهیم که تابع بازگشتی زیر دارای مرتبه اجرایی خطی است.
1// Sum returns the sum 1 + 2 + ... + n, where n >= 1.
2func Sum(n int) int {
3 if n == 1 {
4 return 1
5 }
6 return n + Sum(n-1)
7}فرض میشود تابع $$ T(n)$$ تعداد عملیات ابتدایی اجرا شده به وسیله فراخوانی تابع $$ Sum(n)$$ را نشان میدهد. ۲ خصوصیت برای $$ T(n) $$ قابل شناسایی است:
- چون $$ Sum(1) $$ با استفاده از تعداد عملیات ثابت $$k_1$$ محاسبه میشود، آنگاه $$ T(1) = k_1$$
- اگر $$ n>\;1 $$ باشد، تابع مربوطه تعداد عملیات ثابت $$k_2$$ را اجرا خواهد کرد و علاوه بر آن، فرخوانی بازگشیت به $$ Sum(n-1)$$ نیز خواهد داشت. این فراخوانی بازگشتی عملیاتی به تعداد $$T(n-1)$$ را اجرا خواهد کرد. به طور کلی، رابطه $$ T(n)=k_2 + T(n-1)$$ را خواهیم داشت.
در صورتی که تنها به دنبال تخمینی تقریبی از پیچیدگی زمانی باشیم، نیازی به مشخص کردن مقادیر واقعی ثابتهای $$k_1$$ و $$k_2$$ نخواهیم داشت. بنابراین میتوان مقدار آنها را به صورت $$ k_1 = k_2 = 1$$ در نظر گرفت. بنابراین، مسئله پیدا کردن پیچیدگی زمانی تابع Sum را میتوان به حل رابطه بازگشتی تقلیل داد. بنابراین روابط زیر برقرار خواهند بود:
- $$T(1) = 1 $$
- وقتی $$ n>\;1 $$،آنگاه $$T(n) = 1+ T(n-1)$$
با اعمال روابط فوق به طور متوالی، میتوان $$ T(n)$$ را برای هر عدد مثبت $$ n$$ محاسبه کرد:
$$ T(n) = 1 + T({n-1}) = 1 + (1+T({n-2})) = 2 +T({n-2})= k + T(n-k)$$
$$ n -1 + T(1) = n-1+1 = \theta(n)$$
مرتبه اجرایی تابع بازگشتی جستجوی دودویی
از همین روش بخش قبلی میتوان برای الگوریتمهای بازگشیت پیچیدهتر هم استفاده کرد. نحوه فرمولهسازی تکرارها آسان است، اما حل کردن آنها گاهی دشوارتر خواهد بود. در ادامه، سعی میکنیم مرتبه اجرایی پیادهسازی زیر از جستجوی دودویی را بدست آوریم.
1// Find returns the smallest index i at which x <= a[i].
2// If there is no such index, it returns len(a).
3// The slice must be sorted in ascending order.
4func Find(a []int, x int) int {
5 switch len(a) {
6 case 0:
7 return 0
8 case 1:
9 if x <= a[0] {
10 return 0
11 }
12 return 1
13 }
14 mid := 1 + (len(a)-1)/2
15 if x <= a[mid-1] {
16 return Find(a[:mid], x)
17 }
18 return mid + Find(a[mid:], x)
19}از نماد $$ T(n)$$ به منظور نشان دادن تعداد عملیات ابتدایی اجرا شده به وسیله این الگوریتم در بدترین حالت ممکن یعنی زمانی استفاده میشود که قطعهای مرتبسازی شده از n عنصر دریافت میشود.
این بار هم مسئله تنها به وسیله محاسبه مرتبه اجرایی تقریبی سادهسازی شده است و اجازه میدهیم تمام مقادیر ثابت برابر با یک در نظر گرفته شوند. آنگاه تکرار به صورت زیر خواهد بود:
- $$T(1) = 1 $$
- وقتی $$ n>\;1 $$، آنگاه $$T(n) = 1+ T(n/2)$$
در رابطه ۲، این حقیقت مشخص میشود که تابع، کار ثابتی را به همراه یک فراخوانی بازگشتی به قطعهای با اندازه $$n \over 2$$ انجام میدهد. (در واقع آن قطعه ممکن است در آخر دارای $$ n \over 2 + 1$$ عنصر باشد. اما نگرانی در این خصوص وجود ندارد، زیرا تنها به دنبال تخمینی تقریبی هستین. بار دیگر میتوان راهحلی را به وسیله تقسیم کردنهای متوالی پیدا کرد:
$$ T(n) = 1 + T({n \over 2}) = 1 + (1+T({n \over 4})) = 2 +(1+T({n \over 8})) = k + T({n \over 2^k}))$$
$$ \log n +T({n \over 2^{ \log n}}) = \log n + T(1) = \log n + 1 = \theta(\log n) $$
قضیه اصلی مرتبه اجرایی توابع بازگشتی در ساختمان داده
قضیه اصلی روش و دستورالعملی است که تخمینهایی تقریبی برای دستهای از آن رابطههای بازگشتی ارائه میدهد که اغلب هنگام تجزیه و تحلیل الگوریتمهای بازگشتی با آنها موجه میشویم.
فرض میشود $$ a \ge 1$$ و $$ b >\; 1$$ مقادیری ثابت، $$f(n)$$ تابع و $$ T(n)$$ هم تابعی روی اعداد مثبت تعریف شده به وسیله بازگشت باشد:
$$ T(n) = aT({n \over b}) + f(n)$$
اگر جایی که $$ d \ge 0$$ باشد، $$ f(n) = \theta(n^d)$$:
- اگر $$ a <\;b^d $$ باشد، $$T(n) = \theta (n^d) $$
- اگر $$ a=b^d$$ باشد، $$T(n) = \theta (n^d \log n) $$
- اگر $$ a >\; b^d $$ باشد، $$T(n) = \theta (n^{log_ba}) $$
از ارائه اثبات این قضیه صرف نظر شده است؛ البته اثباتش سخت نیست، اما طولانی است و در حوصله این مقاله نمیگنجد. در واقع برای اثبات قضیه فوق میتوان از جایگزینی پیدرپی، به همان گونهای عمل کرد که در مثالهای قبلی ارائه شدهاند.
حالا بهتر است بررسی شود که آیا قضیه اصلی مرتبه اجرایی توابع بازگشتی در ساختمان داده مثلاً برای مثال مرتبه اجرایی تابع بازگشتی جستجوی دودویی به درستی عمل میکند یا خیر. در این مسئله، هر یک از مقادیر به صورت زیر هستند:
- $$ a = 1$$
- $$b=2$$
- $$ f(n) =1$$
این نشان میدهد که $$f(n) = \theta (n^0) $$، یعنی $$d=0$$ است. ملاحظه میشود که $$ a=b^d$$، بنابراین میتوان از رابطه $$T(n) = \theta (n^d \log n) $$ در قضیه اصلی برای جمعبندی استفاده کرد. پس $$T(n) = \theta (n^d \log n) $$ صحیح است و قضیه اصلی به درستی کار میکند.
تحلیل مرتبه اجرایی در ساختمان داده غیربازگشتی
برای الگوریتمهایی که روی یک ساختمان داده عملیات انجام میدهند، معمولاً ممکن نیست که بتوان رابطهای بازگشتی را پیدا کرد. به جای میتوان کارهایی انجام شده برای هر بخشی از ساختمان داده را شمارش کرد که به وسیله الگوریتم ملاقات شده است. به عنوان مثال میتوان گراف زیر را در نظر گرفت که دارای ۳۶ راس (با رنگ آبی) است و ۳ بخش متصل جداگانه دارد.
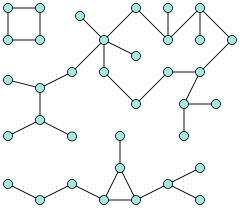
جستجوی «اول-عمق» (Depth-First) الگوریتمی است که تمام آن یالهایی از گراف G را ملاقات میکند که به همان جزء متصل به راس v تعلق دارند.
1Algorithm DFS(G, v)
2 if v is already visited
3 return
4 Mark v as visited.
5 // Perform some operation on v.
6 for all neighbors x of v
7 DFS(G, x)پیچیدگی زمانی این الگوریتم به اندازه و ساختار گراف بستگی دارد. برای مثال، اگر از گوشه بالا سمت چپ گراف بالا شروع کنیم، الگوریتم تنها ۴ راس را ملاقات خواهد کرد. برای محاسبه مرتبه اجرایی یا همان پیچیدگی زمانی، میتوان از تعداد فراخوانیها به DFS به عنوان عملیات ابتدایی استفاده کرد: گزاره if و عملیات علامتگذاری هر دو در زمان ثابت اجرا میشوند و حلقه For برای هر تکرار تنها یک فراخوانی واحد به DFS انجام میدهد.
- پیش از اجرای الگوریتم، تمام راسهای $$ |V| $$ باید به عنوان ملاقات نشده علامتگذاری شوند. مرتبه اجرایی این عملیات برابر با $$ \theta (|V|) $$ است.
- فرض میشود $$E' $$ مجموعه تمام یالها در جزء متصلی باشد که به وسیله الگوریتم ملاقات شده است. الگوریتم ۲ فراخوانی را به DFS برای هر یال $${u\,v} $$ در $$E' $$ انجام میدهد. یک بار وقتی که همسایههای $$ u$$ را ملاقات میکند و یک بار هم زمانی که همسایههای $$ v$$ را ملاقات میکند.
بنابراین، مرتبه اجرایی در این الگوریتم برابر با $$ \theta (|V| + |E'|) $$ است.
مرتبه اجرایی حلقه while
وقتی که لازم باشد کاری را به تعداد n بار انجام دهیم، میتوان از حلقه for در برنامه نویسی یا حلقه While یا هر آنچه استفاده کرد که زبان برنامه نویسی مربوطه (یا حتی شبهکد مربوطه) ارائه میدهد. مشکل اینجاست که در مرتبه اجرایی و نماد O بزرگ تنها به میزان کاری پرداخته میشود که باید انجام شود و به نحوه انجام آن توجهی نشان داده نمیشود. در واقع، مرتبه اجرایی به افزایش میزان کار انجام شده با رشد میزان خروجی مربوط میشود.
حلقههای for و while ساختارهای زبانهای برنامه نویسی به حساب میآیند که برای ابراز انجام عملیات تکراری استفاده میشوند. تجزیه و تحلیل الگوریتمها و تخمین مرتبه اجرایی آنها از زبان پیادهسازی مستقل است و در تحلیل الگوریتمها به ساختارهای مورد استفاده توجهی اهمیتی داده نمیشود. برای مثال، آنچه لازم است به آنچه در ادامه آمده است توجه کنیم:
1Input n
2Do OperationX n timesکارکرد نماد O بزرگ در مرتبه اجرایی کمک میکند تا بتوانیم در مورد پیچیدگی عملیات فوق اظهار نظر کنیم. این قابلیت در موارد بسیاری مفید واقع میشود. برای مثال، امکان محاسبه مرتبه اجرایی در ساختمان داده میتواند به مقایسه زمان اجرای عملیات فوق با عملیات زیر کمک کند:
1Input n
2Input m
3Repeat m OperationX n times.در نماد O بزرگ، مرتبه اجرایی مورد اول برابر با $$ O(n)$$ و پیچیدگی زمانی مثال دوم از مرتبه $$O(m \times n) $$ است (با فرض اینکه اجرای عملیات OperationX در زمان ثابتی انجام شود). میتوان کدهای هر یک از مثالهای بالا را با استفاده از ساختار حلقه دلخواه خود نوشت و تفاوتی وجود ندارد:
1for(int i = 0; i < n; i++) {
2 operationX;
3}کدهای فوق با استفاده از حلقه For برای عملیات اول نوشته شدهاند و کدهای زیر نیز با استفاده از حلقه While برای عملیات یا مثال دوم نوشته شدهاند:
1i = j = 0;
2while(i < n) {
3 j = 0;
4 while(j < m) {
5 operationX;
6 j++;
7 }
8 i++;
9}بنابراین پیچیدگی زمانی یا همان مرتبه اجرایی حلقه While با مرتبه اجرایی حلقه For که پیشتر به آن پرداخته و مثالهایی هم ارائه شد، تفاوتی ندارد و با هم یکسان هستند. در ادامه مثالی با استفاده از حلقه While ارائه شده است:
1x = 0;
2A[n] = some array of length n;
3while (x != A[i]) {
4 i++;
5}همین برنامه و مثال بالا در ادامه با استفاده از حلقه For به جای While پیادهسازی شده است:
1A[n] = some array of length n;
2for(x = 0;x != A[i];i++) {
3
4}پیچیدگی زمانی هر دو مورد یکسان و از مرتبه $$ O(n)$$ است.
مرتبه اجرایی فاکتوریل در ساختمان داده چیست ؟
پیچیدگی زمانی یا مرتبه اجرایی فاکتوریل به صورت O(n!) نشان داده میشود. در واقع O(n!) مرتبه اجرایی فاکتوریل در بدترین حالت به حساب میآید. برای درک بهتر این موضوع، باید به یاد آورد که فاکتوریل در واقع ضرب دنبالهای از n عدد صحیح است. برای مثال، مقدار فاکتوریل عدد ۵ یا همان $$ 5\!$$ به صورت زیر محاسبه میشود:
$$ 5 \times 4 \times 3 \times 2 \times 1 = 120$$
با پیچیدگی زمانی یا همان مرتبه اجرایی فاکتوریل زمانی مواجه میشویم که با جایگشتها و ترکیبها سر و کار داریم. با توجه به نمودار زیر، مشخص میشود که نرخ رشد مرتبه اجرایی فاکتوریل تقریباً عمودی و بسیار نامطلوب است.
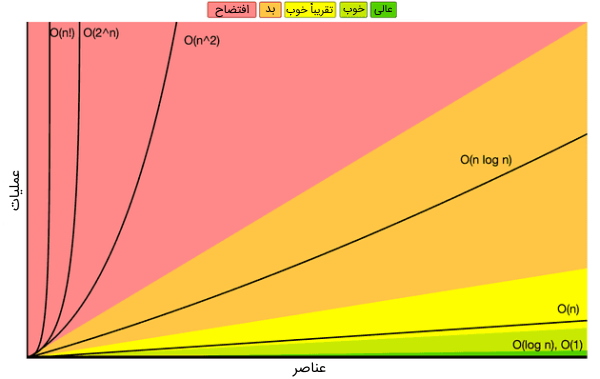
بنابراین مرتبه اجرایی فاکتوریل در ساختمان داده اصلاً مطلوب نیست و این یعنی با رشد اندازه ورودی، زمان اجرای الگوریتم به شدت افزایش خواهد داشت و در پی آن عملکرد و کارایی برنامه به شدت افت میکند. در بسیاری از موارد، ماهیت مسئله باعث میشود که مرتبه اجرایی فاکتوریل داشته باشیم، یعنی مسئله به قدری پیچیده است که راهحلی با مرتبه اجرایی بهتر از پیچیدگی فاکتوریل برای آن پیدا نمیشود.
اینجاست که بحث مسائل NP-Complete مطرح میشود. مثلاً پیچیدگی زمانی الگوریتم Brute Force از نوع مرتبه اجرایی فاکتوریل به حساب میآید. بروت فورس روشی است که در آن برای یافتن بهترین جواب، تمام ترکیبات ممکن محاسبه و بررسی میشوند.
جمعبندی
در این مقاله سعی شد بهطور جامع پیرامون مبحث مهم و پایهای مرتبه اجرایی در ساختمان داده بحث شود. مرتبه اجرایی در ساختمان داده در واقع مرتبهای است که تابع پیچیدگی زمانی یا همان اجرایی از آن تبعیت میکند و در اکثر مواقع با نماد $$ O(n)$$ نمایش داده میشود که به آن «نماد O بزرگ» (Big O Notaion) میگویند.
نمادهای دیگری هم برای توصیف مرتبه اجرایی در ساختمان داده وجود دارند که در این مقاله به آنها هم پرداخته شد و مثالهایی (سوالهایی) هم برای درک بهتر هر یک مطرح شدند. به مرتبه اجرایی توابع چندجملهای، مرتبه اجرایی حلقه For، مرتبه اجرایی توابع بازگشتی، مرتبه اجرایی حلقه While و مرتبه اجرایی فاکتوریل نیز در این مقاله پرداخته شد.











سلام میشه این سوالو با روش trace توضیح بدین؟
int fact(int n)
}
;int i
;f=1
for(i=1;i
ترتیب مرتبه زمانی هایی که زیر عنوان “مقایسه رایج ترین مرتبه های اجرایی در ساختمان داده” نوشتید کاملا غلط هست
با سلام و احترام؛
ضمن تشکر از ارائه بازخورد، ترتیب مرتبههای زمانی اصلاح شد.
از همراهی شما بسیار خوشنود و سپاسگزاریم.