مدولاتور FM — از صفر تا صد

در مطالب قبلی مجله فرادرس به بررسی اهمیت مدولاسیون در مخابرات پرداختیم و همچنین با انواع مختلف روش‌های مدولاسیون دامنه و فاز و فرکانس آشنا شدیم. در این مطلب قصد داریم به بررسی مدارات مختلف مدولاتور (Modulator) فرکانس یا مدولاتور FM بپردازیم. مدولاتورهای FM اصولا دو نوع هستند. یک نوع از مدارهای مدولاتور FM قادر هستند سیگنال‌های «مدولاسیون فرکانس باند باریک» یا NBFM را تولید کنند و نوع دوم از مدولاتورهای FM، سیگنال «مدولاسیون فرکانس پهن باند» یا (WBFM) را تولید می‌کنند. ابتدا مدار مدولاتور فرکانس NBFM را معرفی می‌کنیم.

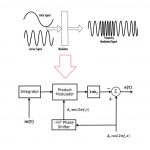
مدولاتور FM باند باریک یا NBFM

برای شروع بهتر است به نکته زیر اشاره کنیم.

فیلم آموزش مبانی سیستم های مخابراتی‎ در فرادرس

کلیک کنید

می‌دانیم که معادله استاندارد مربوط به یک سیگنال مدولاسیون فرکانس باند باریک یا NBFM به صورت زیر نوشته می‌شود:

$$s \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t + 2 \pi k _ f \int m \left ( t \right ) d t \right )$$

$$\Rightarrow s \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) \cos \left ( 2 \pi k _ f \int m \left ( t \right ) d t \right ) -$$

$$A _ c \sin \left ( 2 \pi f _ c t \right ) \sin \left ( 2 \pi k _ f \int m \left ( t \right ) d t \right )$$

در مورد یک سیگنال مدولاسیون FM باند باریک همواره رابطه زیر صحیح و برقرار است:

$$\left | 2 \pi k _ f \int m \left ( t \right ) d t \right | < < 1$$

همچنین می‌دانیم که زمانی که $$\theta$$ بسیار کوچک باشد، $$\cos \theta \approx 1$$ و $$\sin \theta \approx 1$$ صحیح هستند. حال با استفاده از این روابط به دست آمده، می‌توانیم معادله سیگنال مدولاسیون NBFM را به صورت زیر بنویسیم:

$$s \left ( t \right ) = A _ c \cos \left ( 2 \pi f _ c t \right ) - A _ c \sin \left ( 2 \pi f _ c t \right ) 2 \pi k _ f \int m \left ( t \right ) d t$$

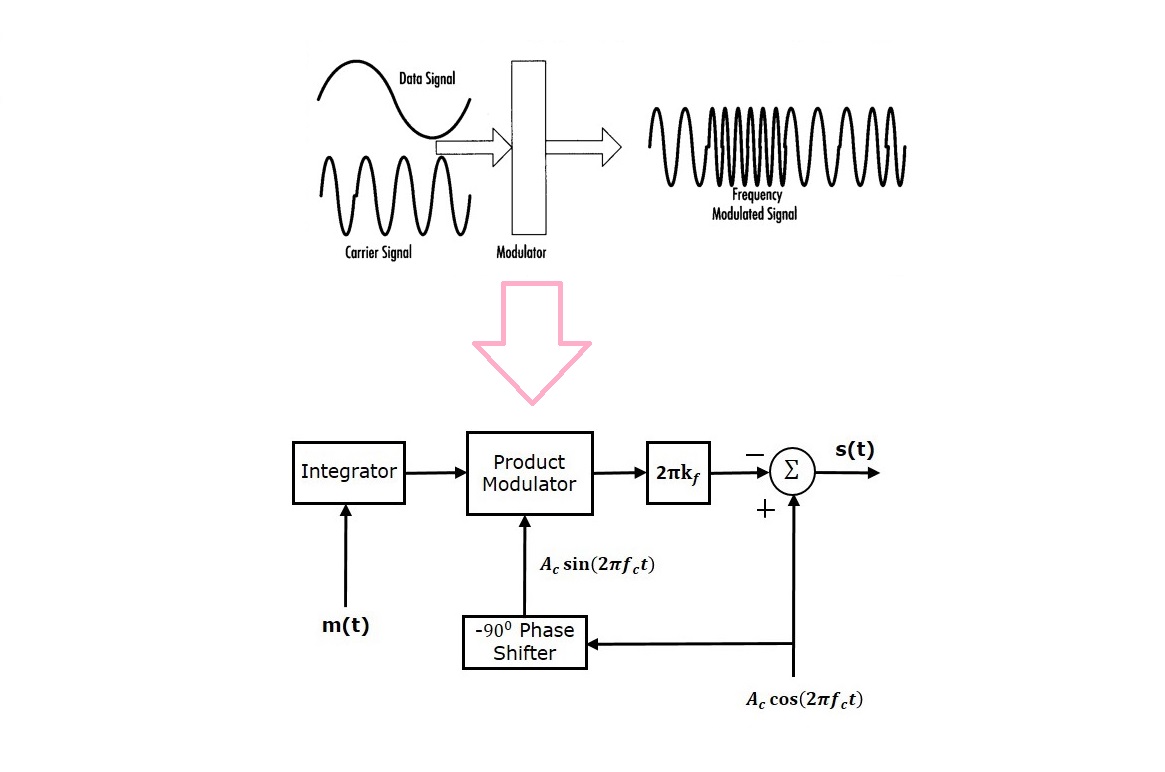
بلوک دیاگرام مربوط به یک مدولاتور FM باند باریک یا NBFM در تصویر زیر نشان داده شده است.

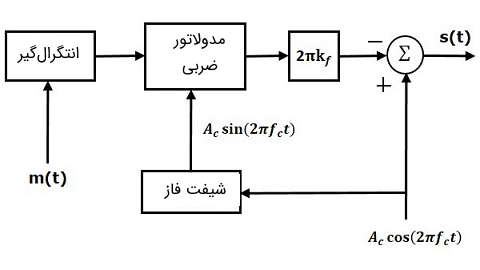
در این بلوک دیاگرام از یک بلوک انتگرال‌گیر برای انتگرال گرفتن از سیگنال پیام $$m \left (t \right )$$ استفاده شده است. همچنین با کمک بلوک شیفت فاز، سیگنال حامل $$A _ c \cos \left ( 2 \pi f _ c t \right )$$ به اندازه ۹۰- درجه شیفت فاز پیدا کرده است تا در نهایت به سیگنال $$A _ c \sin \left ( 2 \pi f _ c t \right )$$ تبدیل شود.

بلوک «مدولاتور ضرب کننده یا ضربی» (Product Modulator) دارای دو ورودی $$\int m \left ( t \right ) d t$$ و $$A _ c \sin \left ( 2 \pi f _ c t \right )$$ است. این بلوک خروجی را تولید می‌کند که برابر با حاصل ضرب این دو سیگنال ورودی باشد. در مسیر پیش روی این سیگنال، یک بلوک $$2 \pi k _ f$$ قرار دارد که سیگنال را در مقدار $$2 \pi k _ f$$ ضرب می‌کند.

بلوک جمع کننده در بلوک دیاگرام نیز دارای دو ورودی است که این ورودی‌ها در واقع همان دو عبارت مربوط به معادله NBFM هستند. علامت‌های مثبت و منفی به سیگنال حامل و نیز ترم دیگر در ورودی بلوک جمع کننده اختصاص داده شده است. در نهایت، خروجی بلوک جمع کننده همان سیگنال مدولاسیون فرکانس باند باریک یا NBFM محسوب می‌شود.

مدولاتور FM پهن باند یا WBFM

برای تولید یک سیگنال مدولاسیون فرکانس پهن باند یا WBFM، در حالت کلی دو روش وجود دارد که عبارتند از «روش مستقیم» (Direct Method) و «روش غیر مستقیم» (Indirect Method).

فیلم آموزش مبانی سیستم های مخابراتی‎ در فرادرس

کلیک کنید

روش مستقیم

این مدولاتور FM، روش مستقیم نام گرفته است؛ زیرا سیگنال مدولاسیون فرکانس WBFM به صورت مستقیم تولید می‌شود. در مدولاتور سیگنال FM پهن باند به روش مستقیم، از یک «اسیلاتور کنترل شده با ولتاژ» (Voltage Controlled Oscillator) یا VCO برای تولید سیگنال WBFM استفاده می‌شود. در واقع مدار اسیلاتور کنترل شده با ولتاژ قادر است سیگنالی را در خروجی خود تولید کند که فرکانس آن با سیگنال ولتاژ ورودی متناسب است. همان طور که می‌دانیم این تعریف بسیار شبیه به تعریف سیگنال مدولاسیون فرکانس یا FM است. در تصویر زیر یک بلوک دیاگرام از نحوه تولید سیگنال مدولاسیون فرکانس یا مدار مدولاتور FM پهن باند WBFM نوع مستقیم نشان داده شده است.

در اینجا سیگنال پیام $$m \left ( t \right )$$ به عنوان ورودی به یک اسیلاتور کنترل شده با ولتاژ یا VCO اعمال شده است. VCO یک خروجی تولید می‌کند که دقیقا همان سیگنال WBFM یا مدولاسیون فرکانس است. در نتیجه روابط زیر صحیح است:

$$f _ i \: \propto \: m \left ( t \right )$$

$$\Rightarrow f _ i = f _ c + k _ f m \left ( t \right )$$

که در این فرمول $$f _ i$$ برابر با فرکانس لحظه‌ای سیگنال مدولاسیون WBFM است.

روش غیرمستقیم

دلیل نام‌گذاری این نوع مدولاتور FM این است که سیگنال مدولاسیون فرکانس پهن باند به صورت غیرمستقیم تولید می‌شود. این امر بدین معنی است که ابتدا یک سیگنال مدولاسیون فرکانس باند باریک یا NBFM را تولید می‌کنیم و سپس با کمک یک ضرب کننده فرکانسی، می‌توانیم سیگنال مدولاسیون فرکانس پهن باند یا WBFM را به دست آوریم. در تصویر زیر بلوک دیاگرام یک مدولاتور FM پهن باند نوع غیرمستقیم نشان داده شده است.

این بلوک دیاگرام اساسا شامل دو طبقه است. در طبقه اول، با استفاده از یک مدولاتور FM پهن باند یا NBFM، یک سیگنال مدولاسیون فرکانس باند باریک را تولید می‌کنیم. در ابتدای این فصل با مدولاتور FM نوع NBFM آشنا شدیم. همچنین می‌دانیم که شاخص مدولاسیون یک سیگنال NBFM کمتر از یک است. به همین دلیل برای به دست آوردن شاخص مدولاسیون سیگنال مدولاسیون فرکانس پهن باند مورد نیاز که بزرگ‌تر از یک است، باید مقدار «ضرب کننده فرکانسی» (Frequency Multiplier) را به صورت مناسبی انتخاب کنیم.

ضرب کننده فرکانسی یک المان غیر خطی است. این مدار یک سیگنال خروجی تولید می‌کند که فرکانس خروجی آن n برابر فرکانس سیگنال ورودی است. در این حالت به n، فاکتور ضرب مدار می‌گویند. اگر سیگنال مدولاسیون NBFM که شاخص مدولاسیون $$\beta$$ آن کمتر از یک است را به عنوان ورودی به یک مدار ضرب کننده فرکانسی وارد کنیم، آن‌گاه ضرب کننده فرکانسی در خروجی خود سیگنالی را تولید می‌کند که شاخص مدولاسیون آن برابر با n ضرب در $$\beta$$ است. همچنین مقدار فرکانس خروجی این مدار، n برابر فرکانس سیگنال NBFM است. گاهی اوقات امکان دارد به چندین طبقه از «میکسرها» (Mixers) و نیز ضرب کننده‌های فرکانسی نیاز داشته باشیم تا در نهایت شاخص مدولاسیون و انحراف فرکانسی را افزایش دهیم و مقدار مورد نظر خود را به دست آوریم.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌‌های مهندسی مخابرات
• آموزش مخابرات ۱
• مجموعه آموزش‌‌های مهندسی الکترونیک
• آموزش مبانی ​الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
• دمدولاسیون دامنه — از صفر تا صد
• مدولاتور AM — از صفر تا صد
• حلقه قفل فاز (PLL) چیست؟ — از صفر تا صد

^^