مدل موج سیار خط – از صفر تا صد

در آموزش‌های قبلی مجله فرادرس، با مدل خط انتقال تک‌فاز و سه فاز آشنا شدیم. در این آموزش، درباره مدل موج سیار خط بحث خواهیم کرد. یک موج سیار (Travelling Wave) روی خط انتقال، اغتشاش گذرایی است که با سرعت ثابتی در طول خط حرکت می‌کند و طی این حرکت شکل آن ثابت باقی می‌ماند. تصویر زیر این موضوع را به خوبی نشان می‌دهد. مثال‌هایی از این اغتشاش صاعقه، حالت گذرای سوئیچینگ، خطاها و... هستند.

در این مطلب، مدل‌های حوزه زمان مختلفی را برای امواج سیار روی خط انتقال به دست خواهیم آورد. بدین منظور، از ساده‌ترین حالت، یعنی خط تکفاز بدون تلفات شروع کرده و در نهایت آن را برای خط تکفاز با تلفات بیان خواهیم کرد.

مدل موج سیار خطوط تکفاز بدون تلفات

یک بخش کوچک به طول $$\Delta x$$ متر را از خط انتقال تکفاز بدون تلفات شکل ۲ در نظر بگیرید.

این مدل، مشابه همان مدل خط با پارامتر توزیع شده کلاسیک است، با این تفاوت که در این مدل، ولتاژها و جریان‌ها توابعی از فاصله $$x$$ و زمان $$t$$ و پارامترهایی حقیقی (نه به صورت فازور) هستند. در مدل پارامتر توزیع شده کلاسیک، ولتاژها و جریان‌ها در حالت ماندگار محاسبه می‌شوند و توابعی از فقط فاصله $$x$$ هستند.

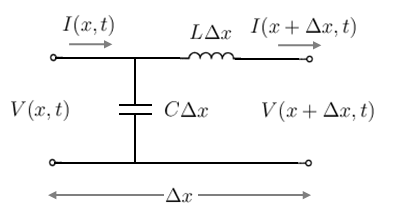
استخراج معادلات ولتاژ و جریان

با تحلیل این مدار با استفاده از KVL و KCL جفت معادله زیر به دست می‌آید:

$$\large V ( x + \Delta x , t ) = V ( x , t ) - L \Delta x \frac { \partial I ( x + \Delta x , t ) } { \partial t } \,$$

$$\large I ( x , t ) = I ( x + \Delta x , t ) + C \Delta x \frac { \partial V ( x , t ) } { \partial t } \,$$

نکات زیر را در نظر داشته باشید:

1. ولتاژ سلف برابر با $$v = L \frac{di}{dt}$$ و جریان گذرنده از خازن $$i = C \frac{dv}{dt}$$ است.
2. از مشتقات جزئی استفاده می‌کنیم، زیرا ولتاژها و جریان‌ها توابعی از زمان و فاصله هستند.

با بازنویسی معادلات بالا، داریم:

$$\large \frac { V ( x + \Delta x , t ) - V ( x , t ) } { \Delta x } = - L \frac { \partial I ( x + \Delta x , t ) } { \partial t } \,$$

$$\large \frac { I ( x + \Delta x , t ) - I ( x , t ) } { \Delta x } = - C \frac { \partial V ( x , t ) } { \partial t } \,$$

با اعمال حد، معادلات معروف تلگرافی (Telegrapher's equations) را به دست می‌آوریم:

$$\large \frac { \partial V ( x , t ) } { \partial x } = - L \frac { \partial I ( x , t ) } { \partial t } \, \; \; \; \; \; (1)$$

$$\large \frac { \partial I ( x , t ) } { \partial x } = - C \frac { \partial V ( x , t ) } { \partial t } \, \; \; \; \; \; ( 2 )$$

با مشتق‌گیری از معادله ولتاژ نسبت به $$x$$ و جریان نسبت به $$t$$ داریم:

$$\large \frac { \partial ^ { 2 } V ( x , t ) } { \partial x ^ { 2 } } = - L \frac { \partial ^ { 2 } I ( x , t ) } { \partial x \partial t } \, \; \; \; \; \; (3)$$

$$\large \frac { \partial ^ { 2 } I ( x , t ) } { \partial x \partial t } = - C \frac { \partial ^ { 2 } V ( x , t ) } { \partial t ^ { 2 } } \, \;\;\;\;\; (4)$$

اکنون با جایگذاری معادله (۴) در معادله (۳)، می‌توان نوشت:

$$\large \frac { \partial ^ { 2 } V ( x , t ) } { \partial x ^ { 2 } } = L C \frac { \partial ^ { 2 } V ( x , t ) } { \partial t ^ { 2 } } \, \; \;\;\;\; (5)$$

به طور مشابه، می‌توانستیم از معادله جریان نسبت به $$x$$ و از معادله ولتاژ نسبت به $$t$$ مشتق بگیریم و جریان را از معادله به دست آوریم:

$$\large \frac { \partial ^ { 2 } I ( x , t ) } { \partial x ^ { 2 } } = L C \frac { \partial ^ { 2 } I (x , t) } { \partial t ^ { 2 } } \, \;\;\;\;\; (6)$$

زوج معادلات (۵) و (۶) به عنوان معادلات موج خط انتقال شناخته می‌شوند.

جواب عمومی هر یک از این معادلات را می‌توان با استفاده از فرمول دالامبر (d'Alembert's Formula) پیدا کرد:

$$\large I ( x , t ) = i ^ { + } ( x - v t ) + i ^ { - } ( x + v t ) \,$$

$$\large V ( x , t ) = v ^ { + } ( x - v t ) + v ^ { - } ( x + v t ) \,$$

که در آن، $$v = \frac{1}{\sqrt{LC}}$$ سرعت انتشار برحسب متر بر ثانیه است.

• $$i^{+}(t)$$ و $$i^{-}(t)$$ توابع جریان هستند.
• $$v^{+}(t)$$ و $$v^{-}(t)$$ توابع ولتاژ هستند.

با استفاده از معادله جریان بالا می‌توانیم معادله ولتاژ را به صورت زیر حل کنیم:

$$\large v ( x , t ) = Z _ { c } \left[ i ^ { +} ( x - v t ) - i ^ { - } ( x + v t ) \right] \,$$

که در آن، $$Z_{c} = \frac{1}{vC} = \frac{\sqrt{LC}}{C} = \sqrt{\frac{L}{C}}$$ امپدانس مشخصه برحسب اهم است.

اهمیت معادلات + و -

معادلات ولتاژ و جریان زیر را داریم:

$$\large I ( x , t ) = i ^ { + } ( x - v t ) + i ^ { - } (x + vt ) \,$$

$$\large V ( x , t ) = Z _ { c } \left[ i ^ { + } ( x - v t ) - i ^ { - } ( x + v t ) \right] \,$$

اما اهمیت $$i^{+}(x - vt)$$ و $$i^{-}(x + vt)$$ در چیست؟

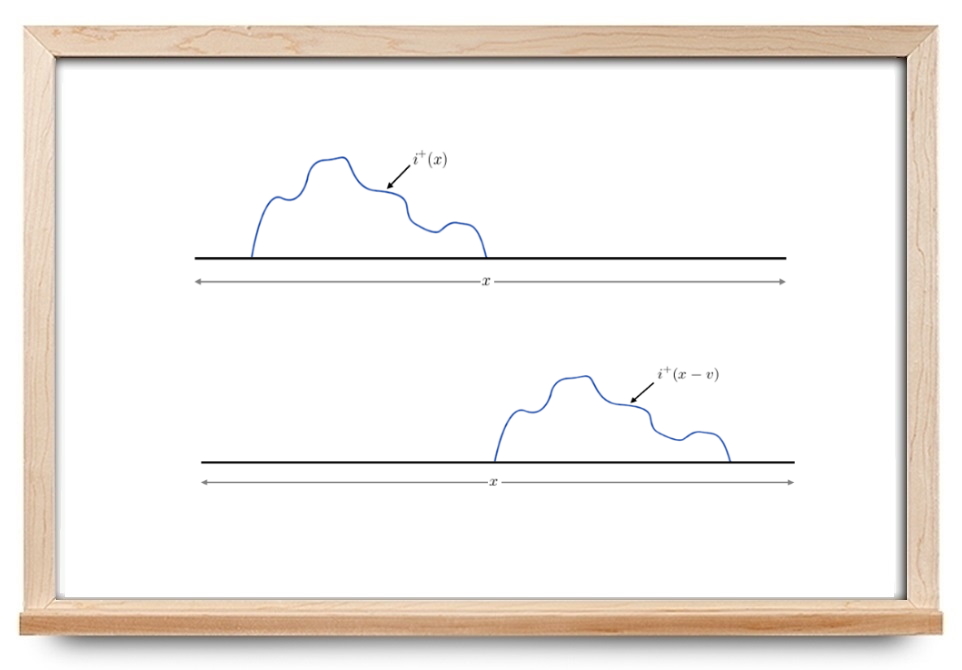
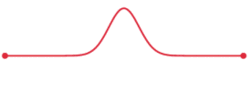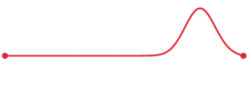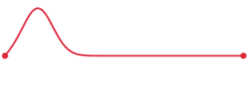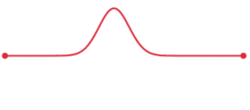
توجه کنید که در زمان $$t = 0$$، تابع $$i^{+}(x)$$ یک شکل موج توزیع شده در فضا را در طول خط انتقال نشان می‌دهد (شکل ۳).

$$i^{+}(x)$$ در زمان $$t = 0$$" width="871" height="223">

اکنون می‌خواهیم بررسی کنیم که در زمان $$t = 1 \; \text{s}$$ چه اتفاقی می‌افتد. در این لحظه تابع $$i^{+}(x - v)$$ شکل مشابهی با تابع بالا دارد، اما به اندازه $$v$$ متر به سمت راست جابه‌جا شده است.

$$i^{+}(x - v)$$ در زمان $$t = 1 \; \text{s}$$" width="862" height="220">

آنچه در اینجا می‌توانیم نتیجه بگیریم، این است که تابع $$i^{+}(x - vt)$$ یک شکل موج اختیاری است که شکل آن تغییری نمی‌کند، اما با گذشت زمان با سرعت $$v$$ متر بر ثانیه به سمت انتهای خط حرکت می‌کند. در این حالت یک موج سیار رو به جلو را پیش‌سو (Forward Travelling Wave) داریم.

با استدلال‌های مشابه می‌توان نتیجه گرفت که تابع $$i^{-}(x + vt)$$ یک شکل موج اختیاری است که در جهت عکس حرکت می‌کند (یعنی به سمت ابتدای خط). در این حالت یک موج سیار رو به عقب یا پس‌سو (Backward Travelling Wave) خواهیم داشت.

مدل موج سیار خطوط تکفاز با تلفات

مدل با پارامتر توزیع شده یک خط تکفاز به طول $$l$$ متر در شکل ۵ نشان داده شده است.

با تحلیل مدار با استفاده از قوانین کیرشهف، مشابه آنچه برای خط بدون تلفات به دست آوردیم، خواهیم داشت:

$$\large \frac { \partial V ( x , t ) } { \partial x } = - I ( x , t ) R - L \frac { \partial I ( x , t ) } { \partial t } \,$$

فیلم آموزش دینامیک سیستم های قدرت ۱ در فرادرس

کلیک کنید

$$\large \frac { \partial I ( x , t ) } { \partial x } = - V ( x , t ) G - C \frac { \partial V ( x , t ) } { \partial t } \,$$

که در آن، $$G = \frac{1}{R_{sh}}$$ رسانایی شنت است.

با مشتق‌گیری از معادله ولتاژ نسبت به $$x$$ و معادله جریان نسبت به $$t$$، داریم:

$$\large \frac { \partial ^ { 2 } V ( x , t ) } { \partial x ^ { 2 } } = - R \frac { \partial I ( x , t ) } { \partial x } - L \frac { \partial ^ { 2 } I ( x , t ) } { \partial x \partial t } \, \;\;\;\;\; (7)$$

$$\large \frac { \partial ^ { 2 } I ( x , t ) } { \partial x \partial t } = - G \frac { \partial V ( x , t ) } { \partial t } - C \frac { \partial ^ { 2 } V ( x , t ) } { \partial t ^ { 2 } } \, \;\;\;\;\; (8)$$

با جایگذاری معادله (۸) در معادله (۷)، خواهیم داشت:

$$\large \frac { \partial ^ { 2 } V ( x , t ) } { \partial x ^ { 2 } } = - R \frac { \partial I ( x , t ) } { \partial x } + L G \frac { \partial V ( x , t ) } { \partial t } + L C \frac { \partial ^ { 2 } V ( x , t ) } { \partial t ^ { 2 } } \, \;\;\;\;\; ( 9 )$$

اگر در معادله بالا $$R = G = 0$$ را قرار دهیم، آنگاه معادله موج خط انتقال مشابه با معادله (۵) در حالت بدون تلفات خواهد بود.

اگرچه با استفاده از فرمول دالامبر یک جواب عمومی برای خط بدون تلفات وجود دارد، اما برای خط دارای تلفات یک جواب به فرم بسته نداریم.

استخراج مدل موج سیار در حوزه فرکانس

در بخش‌های قبلی، مدل موج سیار را در حوزه زمان به دست آوردیم. یک راه دیگر برای بررسی مدل موج سیار، به دست آوردن آن در حوزه فرکانس و تبدیل آن به حوزه زمان است.

همان‌طور که می‌دانیم، مدل پارامتر توزیع شده (حوزه فرکانس) حالت ماندگار که ولتاژ و جریان ابتدا و انتهای خط را به هم مربوط می‌کند، به صورت زیر است:

$$\large \left[ \begin {matrix} \boldsymbol { V _ { s } } \\ \\ \boldsymbol { I _ { s } } \end {matrix} \right] = \left[ \begin {matrix} \cosh ( \boldsymbol { \gamma } l ) & \boldsymbol { Z } _ { c } \sinh ( \boldsymbol { \gamma } l ) \\ \\ \frac { 1 } { \boldsymbol { Z } _ { c } } \sinh ( \boldsymbol { \gamma } l ) & \cosh ( \boldsymbol { \gamma } l ) \end {matrix} \right] \left[ \begin {matrix} \boldsymbol { V _ { r } } \\ \\ \boldsymbol { I _ { r } } \end {matrix} \right] \,$$

که در آن، $$\boldsymbol{\gamma} = \sqrt{\boldsymbol{zy}}$$ ثابت یا ضریب انتشار ($$\text{m}^{-1}$$)، $$\boldsymbol{Z}_{c} = \sqrt{\boldsymbol{\frac{z}{y}}}$$ امپدانس مشخصه برحسب اهم و $$\boldsymbol{z} = R + j \omega l$$ و $$\boldsymbol{y} = G + j \omega C$$، به ترتیب، امپدانس سری و ادمیتانس شنت هستند.

با کمی عملیات جبری، معادلات حالت ماندگار بالا را می‌توان به فرم زیر نوشت:

$$\large \boldsymbol { V _ { r } } + \boldsymbol { Z } _ { c } \boldsymbol { I _ { r } } = ( \boldsymbol { V _ { s } } + \boldsymbol { Z } _ { c } \boldsymbol { I _ { s } } ) e ^ { -\boldsymbol { \gamma } l } \;\;\;\;\; (10)$$

مدل حوزه زمان از تبدیل فوریه معکوس معادله (۱۰) به دست آورد.

در حالت بدون تلفات، (یعنی $$R= G = 0$$)، ضریب انتشار و امپدانس مشخصه به صورت زیر هستند:

$$\large \boldsymbol { \gamma } = \sqrt { \boldsymbol { z y } } = \sqrt { ( j \omega L ) ( j \omega C ) } = j \omega \sqrt { L C }$$

$$\large \boldsymbol { Z } _ { c } = \sqrt { \boldsymbol { \frac { z } { y } } } = \sqrt { \frac { ( j \omega L ) } { ( j \omega C ) } } = \sqrt { \frac { L } { C } }$$

یکی از ویژگی‌های عکس تبدیل فوریه این است که نمایی‌های مختلط در فضای فرکانس را به جابه‌جایی زمانی در حوزه زمان تبدیل می‌کند. بنابراین، با اعمال تبدیل فوریه معکوس به معادله (۱۰)، برای حالت بدون تلفات داریم:

$$\large v _ { r } ( t ) + \sqrt { \frac { L } { C } } i _ { r } ( t ) = v _ { s } ( t - \sqrt { L C } l ) + \sqrt { \frac { L } { C } } i _ { s} ( t - \sqrt { L C } l ) \,$$

حالت بدون تلفات بالا نشان می‌دهد که مقادیر انتهای خط اساساً نسخه‌های جابه‌جا شده (گذشته) مقادیر ابتدای خط هستند که آن‌ها را با استفاده از فرمول دالامبر به دست آوردیم.

در حالت کلیِ با تلفات، امپدانس مشخصه یک ثابت اسکالر نیست (اما تابعی از فرکانس است ($$\boldsymbol{Z}_{c}(\omega)$$)) و ثابت انتشار منجر به یک جابه‌جایی زمانی ساده در حوزه زمان نمی‌شود. بنابراین، معکوس تبدیل فوریه معادله (۱۰) به کانوولوشن منجر خواهد شد:

$$\large v _ { r } ( t ) + z _ { c } ( t ) * i _ { r } ( t ) = \left[ v _ { s } ( t ) + z _ { c } ( t ) * i _ { s } ( t ) \right] * a ( t )$$

که در آن، $$a(t)$$ معکوس تبدیل فوریه $$e^{-\boldsymbol{\gamma}(\omega) l}$$ و $$z_{c}(t)$$ عکس تبدیل فوریه $$\boldsymbol{Z}_{c}(\omega)$$ است. همان‌گونه که می‌توان تصور کرد، انتگرال‌های کانوولوشن در معادله بالا قابل حل نیستند.

مدل موج سیار برای خط‌هایی با چند هادی

مدل موج سیار برای خطوط تکفاز بدون تلفات را می‌توان با جایگزینی مقادیر ولتاژ و جریان با بردارهای $$n \times 1$$ برای $$n$$ هادی بیان کرد. مثلاً برای یک خط سه فاز با سه هادی داریم:

$$\large \boldsymbol { V } ( x , t ) = \left[ \begin {matrix} \boldsymbol { V _ { a } } ( x , t ) \\ \boldsymbol { V _ { b } } ( x, t ) \\ \boldsymbol { V _ { c } } ( x , t ) \end {matrix} \right], \, \; \; \boldsymbol { I } ( x , t ) = \left[ \begin {matrix} \boldsymbol { I _ { a } } ( x , t ) \\ \boldsymbol { I _ { b } } ( x , t ) \\ \boldsymbol { I _ { c }} ( x , t ) \end {matrix} \right]$$

فیلم آموزش ماشین های الکتریکی ۲ در فرادرس

کلیک کنید

همچنین، اندوکتانس و ظرفیت (برحسب واحد طول) را می‌توان با ماتریس‌های $$n \times n$$ برای نشان دادن کوپلینگ بین فازها نمایش داد. برای مثال،‌ در یک خط سه فاز با سه هادی، خواهیم داشت:

$$\large [ L ] = \left[ \begin {matrix} L _ { a a } & L _ { a b } & L _ { a c } \\ L _ { b a } & L _ { b b } & L _ { b c } \\ L _ { c a } & L _ { c b } & L _ { c c } \end {matrix} \right] \, , \; \; \; \; [ C ] = \left[ \begin {matrix} C _ { a a } & C _ { a b } & C _ { a c } \\ C _ { b a } & C _ { b b } & C _ { b c } \\ C _ { c a } & C _ { c b } & C _ { c c } \end {matrix} \right] \,$$

اکنون معادلات موج خط انتقال برای مدل تکفاز (معادلات (5) و (۶) بالا) را می‌توان برای مدل خط با چند هادی بازنویسی کرد:

$$\large \frac { \partial ^ { 2 } \boldsymbol { V } ( x , t ) }{ \partial x ^ { 2 } } = [ L ] [ C ] \frac { \partial ^ { 2 } \boldsymbol { V } ( x , t ) } { \partial t ^ { 2 } } \, \;\;\;\;\; (10)$$

$$\large \frac { \partial ^ { 2 } \boldsymbol { I } ( x , t ) } { \partial x ^ { 2 } } = [ C ] [ L ] \frac { \partial ^ { 2 } \boldsymbol { I } ( x , t ) } { \partial t ^ { 2 } } \, \;\;\;\;\; (11)$$

برخلاف حالت تکفاز، جواب عمومی برای معادلات دیفرانسیل مرتبه دوم (۱۰) و (۱۱) وجود ندارد، زیرا ضرب ماتریسی $$[L][C]$$ معمولاً کامل است (یعنی درایه‌های غیر از قطر اصلی غیرصفر هستند). برای حل چنین معادلات دیفرانسیلی، یک تبدیل مدال برای دکوپله‌سازی فازها لازم است.

بردارهای ولتاژ و جریان با ماتریس‌های $$n\times n$$ تبدیلِ $$[T_{v}]$$ و $$[T_{i}]$$ از حوزه فاز به حوزه مدال تبدیل می‌شوند:

$$\large \boldsymbol { V } ( x , t ) = [ T _ { v } ] \boldsymbol {V' } ( x , t )$$

$$\large \boldsymbol { I } ( x , t ) = [ T _ { i } ] \boldsymbol { I' } ( x , t )$$

که در آن، $$\boldsymbol{V'}(x,t)$$ و $$\boldsymbol{I'}(x,t)$$ بردارهای ولتاژ و جریان مدال هستند:

$$\large \boldsymbol { V' } ( x , t ) = \left[ \begin {matrix} \boldsymbol { V _ { 0 } } ( x ) \\ \boldsymbol { V _ { 1 } } ( x ) \\ \boldsymbol { V _ { 2 } } ( x ) \end {matrix} \right] \, , \;\;\;\; \boldsymbol { I' } ( x , t ) = \left[ \begin {matrix} \boldsymbol { I _ { 0 } } ( x ) \\ \boldsymbol { I _ { 1 } } ( x ) \\ \boldsymbol { I _ { 2 } } ( x ) \end {matrix} \right]$$

ماتریس‌های تبدیلِ $$[T_{v}]$$ و $$[T_{i}]$$ به گونه‌ای انتخاب می‌شوند که به ترتیب، بردارهای ویژه $$[L][C]$$ و $$[C][L]$$ باشند (مقادیر ویژه آن‌ها یکسان است).

در حوزه مدال، معادلات (۱۰) و (۱۱) را می‌توان به صورت مجموعه‌ای از معادلات دکوپله بازنویسی کرد:

$$\large \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { V _ { 0 } } ( x , t ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 1 } } ( x , t ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 2 } } ( x , t ) } { d x ^ { 2 } } \end {matrix} \right] = \left[ \begin {matrix} \lambda _ { 0 } & & \\ & \lambda _ { 1 } & \\ & & \lambda _ { 2 } \end {matrix} \right] \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { V _ { 0 } } ( x , t ) } { d t ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 1 } } ( x , t ) } { d t ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { V _ { 2 } } ( x , t ) } { d t ^ { 2 } } \end {matrix} \right] \, \;\;\;\;\; (12)$$

$$\large \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { I _ { 0 } } ( x ,t ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 1 } } ( x , t ) } { d x ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 2 } } ( x , t ) } { d x ^ { 2 } } \end {matrix} \right] = \left[ \begin {matrix} \lambda _ { 0 } & & \\ & \lambda _ { 1 } & \\ & & \lambda _ { 2 } \end {matrix} \right] \left[ \begin {matrix} \frac { d ^ { 2 } \boldsymbol { I _ { 0 } } ( x , t ) } { d t ^ {2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 1 } } ( x , t ) } { d t ^ { 2 } } \\ \\ \frac { d ^ { 2 } \boldsymbol { I _ { 2 } } ( x , t ) } { d t ^ { 2 }} \end {matrix} \right] \, \;\;\;\;\; (13)$$

این معادلات دیفرانسیل مدال را می‌توان به صورت تکی و با استفاده از فرمول دالامبر حل کرد. برای مثال، جواب برای حالت $$0$$ به صورت زیر است:

$$\large I _ { 0 } ( x , t ) = i _ { 0 } ^ { + } ( x - v _ { 0 } t ) + i _ { 0 } ^ { - } (x + v _ { 0 } t ) \,$$

$$\large V _ { 0 } ( x , t ) = v _ { 0 } ^ { + } ( x - v _ { 0 } t ) + v _ { 0 } ^ { - } ( x + v _ { 0 } t ) \,$$

که در آن، $$v_{0} = \frac{1}{\sqrt{\lambda_0}}$$ سرعت انتشار برای حالت $$0$$ و برحسب متر بر ثانیه است. همچنین، $$i^{+}(t)$$ و $$i^{-}(t)$$ توابع جریان و $$v^{+}(t)$$ و $$v^{-}(t)$$ توابع ولتاژ برای مد $$0$$ هستند.

بعد از آنکه مقادیر حوزه مدال محاسبه شدند، آنگاه مقادیر حوزه فاز را می‌توان با اعمال تبدیل معکوس به دست آورد.

در نهایت، باید این نکته را متذکر شد که جواب عمومی با استفاده تبدیل مدال فقط بر خطوط چندهادی بدون تلفات اعمال می‌شود. یک خط با تلفات موضوعاتی از قبیل جملات کوپلینگ دارد که موجب می‌شود نتوان از فرمول دالامبر استفاده کرد.

وابستگی پارامترهای خط به فرکانس

تاکنون اندوکتانس ($$L$$)، ظرفیت ($$C$$)، مقاومت ($$R$$) و هدایت ($$G$$) بر واحد طول پارامترهای خط را ثابت فرض کرده و برای محدوده‌ای از فرکانس‌ها به دست آوردیم. البته، این فرض معتبر نیست، خصوصاً در فرکانس‌های بالاتر. برای مثال، اثر پوستی منجر به مقاومت‌های بالاتر در فرکانس‌های بالاتر می‌شود. بنابراین، صحیح‌تر این است که پارامترهای خط را وابسته به فرکانس بنویسیم؛ یعنی به صورت $$L(\omega)$$، $$C(\omega)$$، $$R(\omega)$$ و $$G(\omega)$$.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• سیستم پریونیت (Per-Unit) — از صفر تا صد
• پارامترهای خط انتقال در مهندسی قدرت — به زبان ساده
• پخش بار نیوتن رافسون در متلب — از صفر تا صد

^^