مدل استاندارد ذرات — به زبان ساده

نظریه‌ها و اکتشافات هزاران فیزیکدان از دهه 1930 منجر به بینشی چشمگیر در ساختار اساسی ماده شده است و مشخص کرده که همه چیز در جهان از چند بلوک اساسی به نام ذرات بنیادی ساخته شده که توسط چهار نیروی اساسی اداره می‌شود. بهترین درک ما از چگونگی ارتباط این ذرات و سه نیرو با یکدیگر در مدل استاندارد فیزیک ذرات محصور شده است. مدل استاندارد ذرات در اوایل دهه 1970 توسعه یافته و تقریباً همه نتایج تجربی را با موفقیت توضیح داده و طیف گسترده‌ای از پدیده‌ها را به طور دقیق پیش‌بینی کرده است. با گذشت زمان و انجام آزمایشات فراوان مدل استاندارد به عنوان یک تئوری فیزیک کاملاً آزمایش شده ثابت شده است.

مدل استاندارد چیست؟

مدل استاندارد نامی است که در دهه 1970 به نظریه ذرات بنیادی و نحوه تعامل آن‌ها با یکدیگر داده شده است. این نظریه تمام آنچه در مورد ذرات زیر اتمی در آن زمان شناخته شده بود را شامل می‌شد و وجود ذرات اضافی را نیز پیش‌بینی کرد.

هفده ذره شناخته شده با نام‌ در مدل استاندارد وجود دارند که در تصویر زیر نیز نشان داده شده و طبقه‌بندی شده‌اند. آخرین ذرات کشف شده بوزون W و Z در سال 1983، کوارک «بالا» (Top) در سال 1995، تاو نوترینو در سال 2000 و بوزون هیگز در سال 2012 بود.

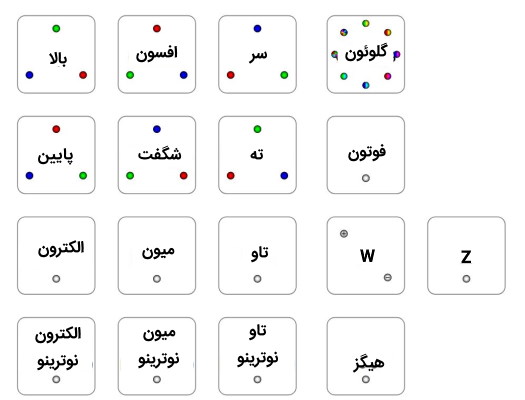
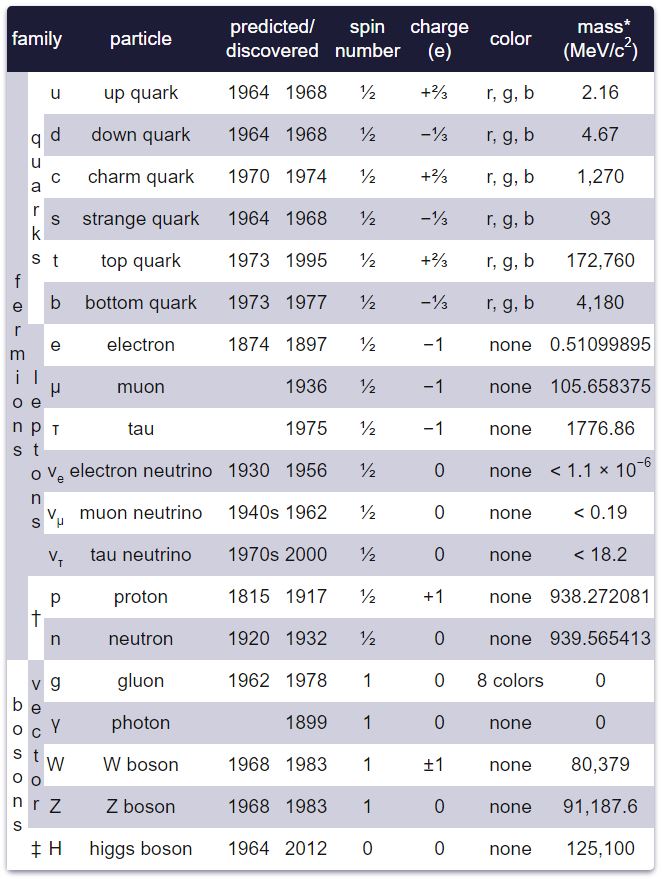
خانواده‌های ذرات بنیادی در مدل استاندارد

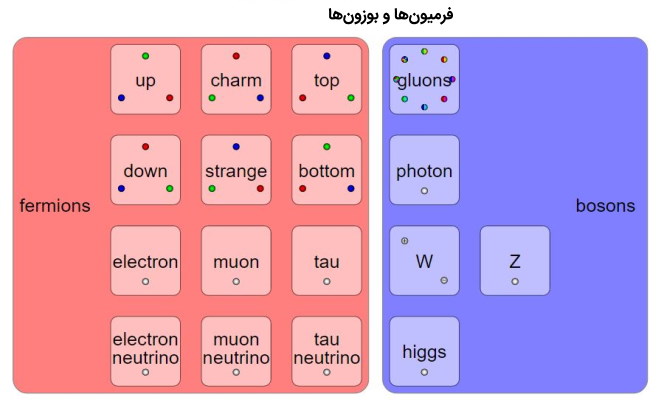
ذرات بنیادی اگر عناصر سازنده ماده باشند فرمیون نامیده می‌شوند و اگر واسطه‌های فعل و انفعالات باشند به نام بوزون شناخته می‌شوند. در مدل استاندارد دوازده فرمیون و پنج بوزون وجود دارد.

رفتار فرمیون‌ها از یک قانون آماری که توسط «انریکو فرمی» (Enrico Fermi) (1954-1901) از ایتالیا، «پائول دیراک» (Paul Dirac) (1984-1902) از انگلستان و «ولفگانگ پائولی» (Wolfgang Pauli) (1958-1900) از اتریش ارائه شد پیروی می‌کنند و آن را «اصل طرد» (exclusion principle) می‌نامند. به زبان ساده فرمیون‌ها نمی‌توانند همزمان مکان مشابه را اشغال کنند و به بیان رسمی‌تر هیچ دو فرمیون را نمی‌توان با عدد کوانتومی یکسان توصیف کرد.

لپتون‌ها و کوارک‌ها فرمیون هستند، همچنین مواردی مانند پروتون‌ها، نوترون‌ها، اتم‌ها‌، مولکول‌ها، مردم و دیوارها نیز از فرمیون ساخته می‌شوند. این با مشاهدات ماکروسکوپی ما در زندگی روزمره همخوانی دارد و بر این اساس مردم نمی‌توانند از میان دیوارها عبور کنند مگر اینکه دیوار از سر راه آن‌ها برداشته شود.

در مقابل بوزون‌ها مشکلی برای اشغال همزمان یک مکان ندارند و به بیانی دیگر دو یا چند بوزون ممکن است با اعداد کوانتومی یکسان توصیف شوند. قوانین آماری که بوزون‌ها از آن‌ها پیروی می‌کنند ابتدا توسط «ساتیندرا بوز» (Satyendra Bose) (1894-1974) از هند و سپس توسط «آلبرت اینشتین» (Albert Einstein) (1879–1955) از آلمان معرفی شد. گلوئون‌ها، فوتون‌ها، W ،Z و هیگز همه بوزون هستند. این ذرات به عنوان اجزای سازنده‌ای که نور و سایر تابش‌های الکترومغناطیسی را تشکیل می‌دهند شناخته می‌شوند و در میان این ذرات فوتون بوزون‌هایی هستند که مستقیم‌ترین تجربه را با آن‌ها داریم. در تجربه روزمره خود هرگز نمی‌بینیم که پرتوهای نوری به یکدیگر برخورد کنند در حقیقت فوتون‌ها مانند شبح هستند و بدون تأثیر بر یکدیگر از میان هم عبور می‌کنند.

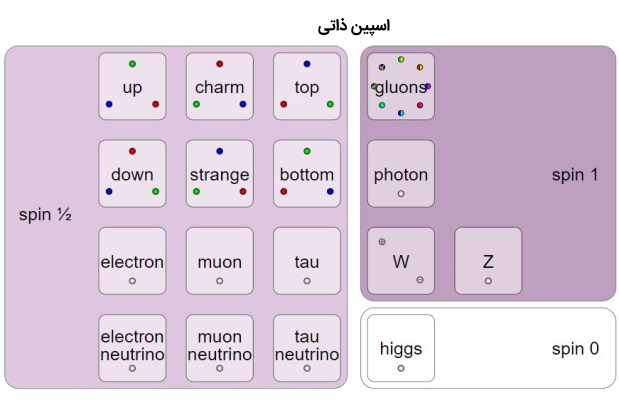
ذرات بنیادی دارای یک تکانه زاویه‌ای اسپین ذاتی یا S نیز هستند. صفت ذاتی به معنای اصلی یا اساسی برای ذره است. ذرات بنیادی چرخش ندارند زیرا کسی آن‌ها را می‌چرخاند، آن‌ها فقط می‌چرخند یا بهتر بگوییم آن‌ها فقط یک مقدار قابل اندازه گیری با واحدهای مشابه حرکت زاویه‌ای دارند. در فیزیک امروزی ذرات بنیادی فاقد ویژگی هستند و مانند یک نقطه ریاضی در نظر گرفته می‌شوند.

برای درک چیزی تحت عنوان چرخش به توصیفی مانند جلو و پشت نیاز است. ذرات نقطه‌ای چیزی شبیه به این ویژگی ندارند. فیزیک ذرات به بهترین شکل با ریاضیات توصیف می‌شود. «اسپین» (Spin) عبارتی مناسب برای یک کیفیت قابل اندازه گیری است و توصیف یک واقعیت نیست.

هر ذره بنیادی با یک عدد کوانتومی اسپین s همراه است که اغلب به آن عدد اسپین یا اسپین می‌گویند. اسپین برابر با حاصلضرب هر عدد صحیح در نیم است. فرمیون‌ها دارای اعداد اسپین کوانتومی نیمه صحیح $$(\frac{1}{2}, 1\frac{1}{2}, 2\frac{1}{2}, etc.)$$ و بوزون‌ها دارای اعداد اسپین کوانتومی صحیح $$(0,1,2,etc.)$$ هستند. در میان این اعداد هیچ عدد اسپین دیگری امکان پذیر نیست و اسپین یک کمیت کوانتیده است.

فرمیون‌های ابتدایی اسپین $$\frac{1}{2}$$ دارند. ذرات ساخته شده از ترکیب فرمیون‌ها یک اسپین کلی دارند که ترکیبی از اسپین‌های منفرد است. یک باریون که از سه کوارک تشکیل شده دارای اسپین کل $$\frac{1}{2}$$ یا $$\frac{1}{2}1$$ است، زیرا این مقادیر تنها ترکیبات غیرمنفی و ممکن $$\frac{1}{2}\pm\frac{1}{2}\pm\frac{1}{2}$$ هستند. این موضوع نشان می‌دهد که همه باریون‌ها (به عنوان مثال پروتون‌ها و نوترون‌ها) نیز فرمیون هستند. به همین ترتیب یک مزون متشکل از یک کوارک و یک آنتی کوارک با اسپین کل 0 یا 1 ترکیب می‌شود زیرا این مقادیر تنها مقادیر غیرمنفی و ممکن از $$\frac{1}{2}\pm\frac{1}{2}$$ هستند. این موضوع نشان می‌دهد که همه مزون‌ها (به عنوان مثال پیون باقیمانده از فعل و انفعالات قوی) نیز بوزون هستند.

بوزون‌های حمل کننده نیرو در مدل استاندارد (گلوئون‌ها، فوتون‌ها، W و Z) زمانی که با میدان‌های برداری همراه باشند اسپین یک دارند. بوزون هیگز مربوط به یک میدان اسکالر است بنابراین دارای اسپین صفر است. اگر ذره‌ای از میدان گرانشی کشف شود به آن گراویتون گفته می‌شود و از آنجا که با یک میدان تانسوری همراه است اسپین 2 خواهد داشت.

تانسور یک شی ریاضی است که پیچیده‌تر از یک بردار و به نوبه خود پیچیده‌تر از یک اسکالر است. در حقیقت روند به این صورت است: یک میدان اسکالر بدون جهت ذره‌ای با اسپین 0، یک میدان برداری با جهت ذره‌ای با اسپین 1 و یک میدان تانسوری که فضا را از دو جهت کشیده و فشرده می‌کند ذره‌ای با اسپین 2 می‌دهد.

تمام ذرات بنیادی و ترکیبات آن‌ها دارای عدد کوانتومی اسپین هستند که با s نمایش داده می‌شوند، این کمیت با یک تکانه زاویه‌ای اسپین که با S نمایش داده می‌شود همراه است. واحد SI حرکت زاویه‌ای کیلوگرم متر مربع در ثانیه $$[kg \frac{m^2}{s}]$$ یا به طور معادل ژول ثانیه $$[J s]$$ است که برای ذرات بنیادی واحدی بسیار بزرگ است و در عوض از $$\hbar$$ استفاده می‌شود که ثابت کاهیده پلانک است. همچنین باید اضافه کرد که عدد کوانتومی اسپین s (که فقط یک عدد است) و تکانه زاویه‌ای اسپین S (که یک عدد با واحد است) از نظر عددی یکسان نیستند و در عوض با یک معادله غیر شفاف به یکدیگر مرتبط می‌شوند.

$$\large S=[s(s+1)]^{\frac{1}{2}}\hbar$$

برای ذراتی با عدد کوانتومی اسپین صفر، تکانه‌ زاویه‌ای اسپین به صورت زیر و برابر با $$0 \hbar$$ به دست می‌آید:

$$\large S(0)=[0(0+1)]^{\frac{1}{2}}\hbar=0 \hbar$$

برای عدد کوانتومی اسپین بالاتر، تکانه زاویه‌ای اسپینی افزایش می‌یابد اما غیر از این چیز دیگری نیست که بتوان به سادگی بیان کرد.

$$\large S(\frac{1}{2})=[\frac{1}{2}(\frac{1}{2}+1)]^{\frac{1}{2}}\hbar=\frac{\sqrt{3}}{2} \hbar$$

$$\large S(1)=[1(1+1)]^{\frac{1}{2}}\hbar=\sqrt{2} \hbar$$

$$\large S(1\frac{1}{2})=[\frac{3}{2}(\frac{3}{2}+1)]^{\frac{1}{2}}\hbar=\frac{\sqrt{15}}{2} \hbar$$

$$\large S(2)=[2(2+1)]^{\frac{1}{2}}\hbar=\sqrt{6} \hbar$$

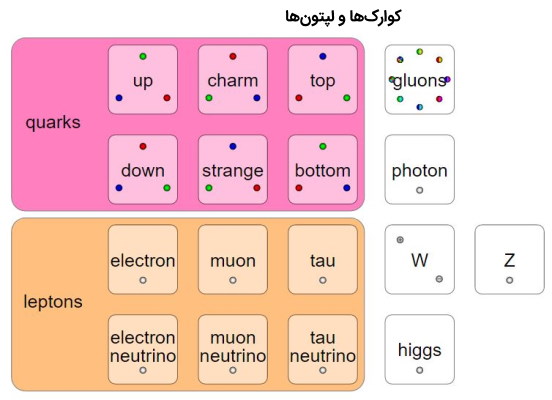
فرمیون‌ها به دو گروه شش‌تایی تقسیم می‌شوند، به ذراتی که باید به یکدیگر متصل باشند کوارک و به ذراتی که می‌توانند به طور مستقل وجود داشته باشند لپتون می‌گویند.

واژه کوارک در اصل در یک خط از رمان Finnegans Wake که توسط نویسنده ایرلندی جیمز جویس (1882–1941) نوشته شده، آمده است. شخصیت اصلی کتاب یک تاجر به نام هامفری شمپدن ارویکر است که در خواب می‌بیند در حال سرو کردن نوشیدنی برای یک مرغ دریایی است و پرنده به جای درخواست سه چهارم لیوان برای آقای مارک، عصبی می‌گوید: سه کوارک برای مارک ماستر! از آنجا که در آن زمان نظریه مدل پیش استاندارد فقط با سه کوارک کامل می‌شد، این نام تا حدودی معنادار بود و استفاده از آن رایج شد. امروزه مدل استاندارد کامل به شش کوارک نیاز دارد ولی این باعث نشده است که کلمه کوارک کمتر استفاده شود. کوارک شش حالت کوارک «بالا» (Up)، «پایین» (Down)، «افسون» (Charm)، «شگفت» (Strange)، «سر» (Top) و «ته» (Bottom) دارد، با این حال نام این حالت‌های کوارک اساساً بی‌معنی است.

کوارک‌ها به انواع دوتایی و سه‌تایی نیز شناخته می‌شوند. کوارک‌های سه تایی را باریون می‌نامیم که اصطلاحی است که از کلمه یونانی βαρύς مشتق شده و به معنی سنگین است. کوارک‌های دوتایی مزون نامیده می‌شوند و این اصطلاحی است که از کلمه یونانی μέσος گرفته شده و به معنی متوسط است.

در مجموع باریون‌ها (کوارک‌های سه‌تایی)، مزون‌ها (کوارک‌های دوتایی) و کوارک‌ها (ذرات بنیادی) به عنوان هادرون شناخته می‌شوند که از کلمه یونانی αδρός گرفته شده و به معنای ضخیم، قوی، عظیم یا بزرگ است. این نام در حقیقت اشاره به توانایی کوارک‌های نقطه‌ای دارد که می‌توانند به یکدیگر متصل شده و ذراتی را که به نوعی محکم هستند را تشکیل دهند.

شش فرمیون دیگر لپتون نامیده می‌شوند نامی که از کلمه یونانی λεπτός گرفته شده و به معنی لاغر، ظریف، سبک یا کوچک است. این ذرات نیازی به اتصال به یکدیگر ندارند و این ویژگی سبب می‌شود تا آن‌ها به معنی واقعی کلمه نازک باشند. در ابتدا لپتون‌ها ذرات سبک و هادرون‌ها ذرات سنگین در نظر گرفته می‌شدند اما کشف تائو لپتون در 1975 این قانون را نقض کرد. تاو (سنگین‌ترین لپتون) تقریباً دو برابر یک پروتون (سبک‌ترین هادرون) جرم دارد.

باریون‌های موجود در هسته (پروتون و نوترون) نوکلئون نامیده می‌شوند. معادل کلمه لاتین kernel هسته یا nucleus است. باریون‌هایی که حداقل حاوی یک کوارک شگفت باشند اما کوارک افسون، ته و سر نداشته باشند هایپرون نامیده می‌شوند. کلمه یونانی که معنای فراتر را بدهد υπέρ (yper) است که به پیشوند انگلیسی hyper- تبدیل می‌شود. هایپرون‌ها ذراتی هستند که معنای ذرات غیرعادی را می‌رسانند.

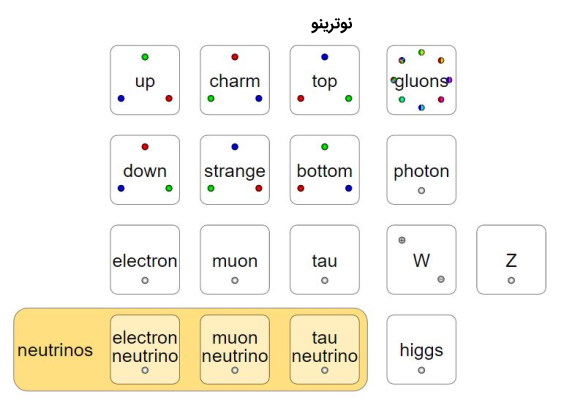
نوترینوها یک زیر گروه مهم در لپتون‌ها هستند که در سه حالت وجود دارند. این سه حالت عبارت از الکترون، میون و تاو هستند که با الکترون نوترینو، میون نوترینو و تاو نوترینو نمایش داده می‌شوند. جرم نوترینوها بسیار کم است (حتی برای لپتون‌ها) و با سایر ذرات برهم‌کنش ضعیفی دارند و به همین دلیل تشخیص آن‌ها بسیار دشوار است.

نام نوترینوها به نوعی بازی با کلمات است. کلمه ایتالیایی نوترون (neutrone) نوشتاری شبیه به کلمه خنثی (neutro) دارد که در انتهای آن یک پسوند تقویت کننده (-one) قرار داده می‌شود. در حقیقت در زبان ایتالیایی نوترون به معنای ذره خنثی اصلی است. با جایگزین کردن پسوند -one با پسوند ino- این کلمه به نوترینو یا neutrino تبدیل می‌شود که به معنای یک ذره خنثی کوچک است که مفهوم و نقش نوترینو را نیز می‌رساند. نوترینو یک ذره کوچک و خنثی است.

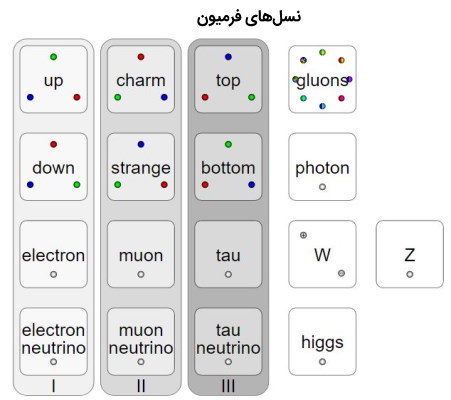
فرمیون‌ها متعلق به یکی از سه نسل شناخته شده «معمولی» (Ordinary)، «عجیب» (Exotic) یا «خیلی عجیب» (Very Exotic) هستند. ذرات نسل معمولی یا نسل I می‌توانند با هم ترکیب شده و هادرون‌هایی با طول عمر موثر بی‌نهایت ایجاد کنند (به عنوان مثال اتم‌های پایدار ساخته شده از الکترون، پروتون و نوترون از این نسل هستند). ذرات نسل II یا عجیب همیشه هادرون‌های ناپایدار تشکیل می‌دهند. طولانی‌ترین طول عمر هادرون حاوی کوارک نسل دوم را ذره لامبدا دارد که از کوارک بالا، پایین و شگفت ساخته شده است. طول عمر این ذره کمتر از یک میلیاردم ثانیه است که برای یک هادرون ناپایدار زمانی طولانی در نظر گرفته می‌شود. ذرات نسل III یا خیلی عجیب رفتارهای متفاوتی را از خود نمایش می‌دهند. کوارک ته نسبت به کوارک شگفت رفتار خیلی متفاوتی نشان نمی‌دهد اما کوارک سر آنقدر طول عمر کوتاهی دارد که زمان لازم برای انجام هیچ کاری را ندارد و حتی قبل از اینکه عالم از وجود آن آگاه شود از هم می‌پاشد. حضور کوارک‌های سر تنها از آثار ناشی از تابش‌ و پرتوهای مربوط به آن‌ها تایید می‌شود.

فعل و انفعالات ذرات بنیادی

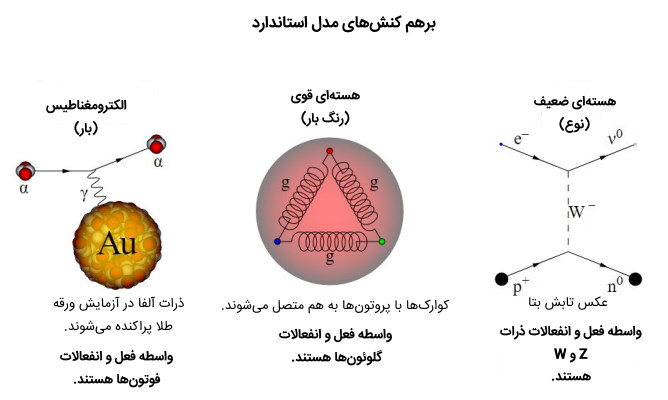
سه نیرو از چهار نیروی بنیادی عالم در مدل استاندارد فیزیک ذرات گنجانده شده است که عبارتند از نیروهای الکترومغناطیس، نیروی هسته‌ای قوی و نیروی هسته‌ای ضعیف. در حقیقت گرانش در مدل استاندارد قابل تعریف و بررسی نیست.

هر نیرو به دلیل خاصیتی از یک ذره بین ذرات وارد عمل می‌شود بارالکتریکی باعث ایجاد نیروی الکترومغناطیس، رنگ باعث ایجاد نیروی هسته‌ای قوی و نوع ذره باعث ایجاد نیروی هسته‌ای ضعیف می‌شود. بوزون‌های مرتبط با هر نیرو را بوزون‌های پیمانه‌ می‌نامند این پیمانه برای نیروی الکترومغناطیس فوتون، برای نیروی هسته‌ای قوی گلوئون و بوزون‌های W و Z برای نیروی هسته‌ای ضعیف هستند. در ادامه هر سه ویژگی ذرات بنیادی را به تفکیک بررسی می‌کنیم.

بار الکتریکی ذرات بنیادی در مدل استاندارد

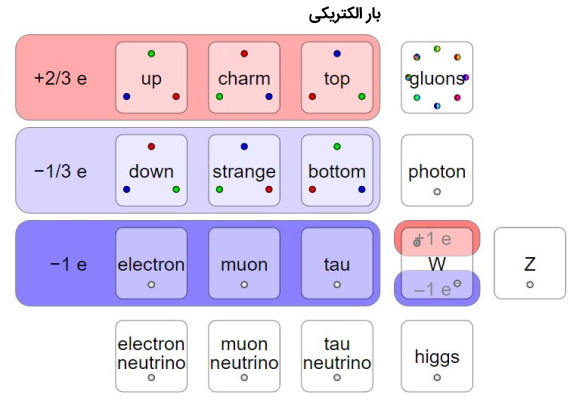
بار الکتریکی خاصیتی از ماده است که باعث پدیده‌های الکتریکی و مغناطیسی می‌شود که در مجموع به عنوان نیروی الکترومغناطیس شناخته می‌شود. بار الکتریکی کمیتی کوانتیده است به این معنی که فقط در مقادیر گسسته و به صورت ضرایب یا کسری از $$e=1.6\times 10^{-19}$$ کولن وجود دارد.

ذراتی که به طور مستقل وجود دارند یعنی الکترون، میون و تاو مضربی از بار ابتدایی را با خود حمل می‌کنند در حالی که کوارک‌ها کسری از بار ابتدایی را حمل می‌کنند ($$+\frac{2}{3}e$$ یا $$-\frac{1}{3}e$$). کوارک‌ها همیشه در گروه‌هایی قرار می‌گیرند که در نهایت بار کل آن‌ها یک عدد صحیح است و به همین دلیل تا به حال کسی بار کسری اندازه‌گیری نکرده است. علاوه بر این از آنجا که بارهای مخالف یکدیگر را جذب می‌کنند الکترون‌ها توسط پروتون‌ها جذب می‌شوند و اتم‌هایی را تشکیل می‌دهند که بار الکتریکی آن‌ها در کل صفر است و خنثی هستند. به همین دلیل معمولاً متوجه ماهیت الکتریکی ماده نمی‌شویم.

برهم کنش الکترومغناطیس

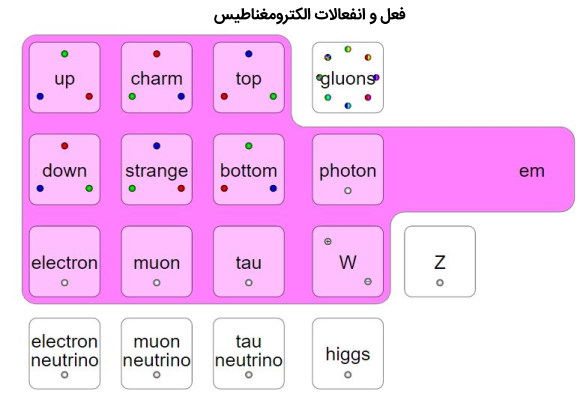
ذرات باردار با تبادل فوتون‌ها که حامل نیروی الکترومغناطیسی هستند برهم کنش می‌کنند. هرگاه الکترونی یک الکترون دیگر را دفع کند یا هر الکترونی به دور یک هسته بچرخد یک فوتون نقش بازی می‌کند. فوتون‌ها بدون جرم، بدون بار و دامنه حرکتی نامحدود هستند. مدل ریاضی مورد استفاده برای توصیف برهم کنش ذرات باردار از طریق تبادل فوتون‌ها به عنوان الکترودینامیک کوانتومی (QED) شناخته می‌شود.

بار رنگ ذرات بنیادی

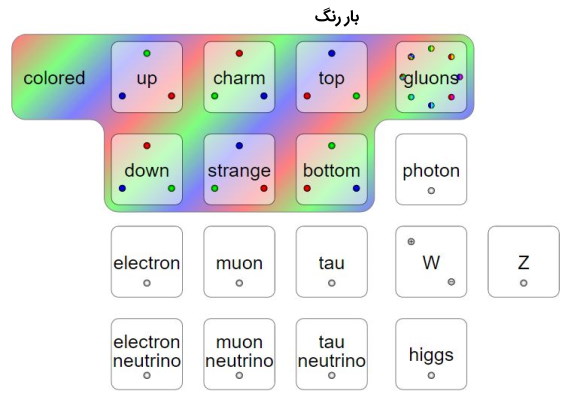
کوارک‌ها به کوارک‌های دیگر می‌چسبند زیرا دارای مشخصه‌ای هستند که به آن رنگ یا بار رنگی می‌گویند. کوارک‌ها در یکی از سه رنگ قرمز، سبز و آبی وجود دارند. اما این اصطلاح مانند رنگ اپتیکی که ما از آن یاد می‌کنیم نیست، در حقیقت کوارک‌ها بسیار کوچک هستند که حتی دیده شوند و بنابراین هرگز نمی‌توانند خاصیت ادراکی مانند رنگ داشته باشند. این نام به دلیل تشابه فیزیکی با رنگ اپتیکی اینگونه انتخاب شده است.

در حقیقت موضوع از این قرار است که نور قرمز به علاوه نور سبز و نور آبی در نظر ما انسان‌ها به عنوان نور سفید یا بی‌رنگ ظاهر می‌شود. یک باریون ترکیبی سه‌تایی از یک کوارک قرمز، یک کوارک سبز و یک کوارک آبی است. با قرار دادن این سه ذره در کنار هم یک ذره با رنگ خنثی به دست می‌آورید. یک رنگ به علاوه رنگ مخالف آن نیز نور سفید می‌دهد، برای مثال نور قرمز به علاوه نور فیروزه‌ای برای انسان مانند نور سفید به نظر می‌رسد. یک مزون یک دوتایی از یک کوارک رنگی و یک ضد کوارک ضد رنگ است، با قرار دادن این دو در کنار هم یک ذره با رنگ خنثی به دست می‌آید.

چیزی در مورد رنگ وجود دارد که باعث می‌شود خودش را از هر چیزی که بزرگتر از یک هسته است پنهان کند. کوارک‌ها تحمل جدا بودن از یکدیگر را ندارند. آن‌ها فقط باید به هم بپیوندند و همیشه باید این کار را به شکلی انجام دهند که رنگ آن‌ها از دنیای خارج مخفی بماند. وقتی کوارک‌ها دور هم جمع می‌شوند هرگز یک رنگ نسبت به رنگ دیگر مورد توجه واقع نمی‌شود و این موضوع بدان معنی است که ماده از لحاظ رنگی تا حد بسیار زیادی خنثی است.

برهم‌‌کنش هسته‌ای قوی

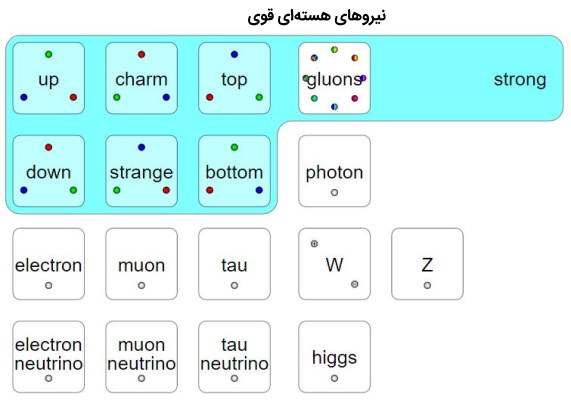
ذرات رنگی توسط گلوئون‌های مناسب به یکدیگر متصل می‌شوند. گلوئون‌ها نیز رنگی هستند اما رنگی بودن آن‌ها بسیار پیچیده‌تر از کوارک‌ها است. شش گلوئون از هشت گلوئون دارای دو رنگ، یکی دارای چهار رنگ و دیگری دارای شش رنگ است. گلوئون‌ها کوارک‌ها را به هم می‌چسباند اما آنها خودشان نیز به یکدیگر می‌چسبند و یک نتیجه بدیهی این امر این است که دامنه حرکتی و تاثیر آن‌ها فراتر از هسته نخواهد بود.

مدل ریاضی مورد استفاده برای توصیف برهم کنش ذرات رنگی از طریق تبادل گلوئون‌ها به عنوان کرومودینامیک کوانتومی (QCD) شناخته‌ می‌شود. به کل این آشفتگی چسبنده نیروی هسته‌ای قوی یا فعل و انفعالات قوی گفته می‌شود. این نام به این دلیل انتخاب شده است که منجر به ایجاد نیروهایی در هسته می‌شود که از نیروی الکترومغناطیسی قویتر هستند. بدون وجود نیروی هسته‌ای قوی هر هسته‌ای خود را به قسمت‌های کوچکتر تبدیل می‌کند.

نوع فرمیون‌ها

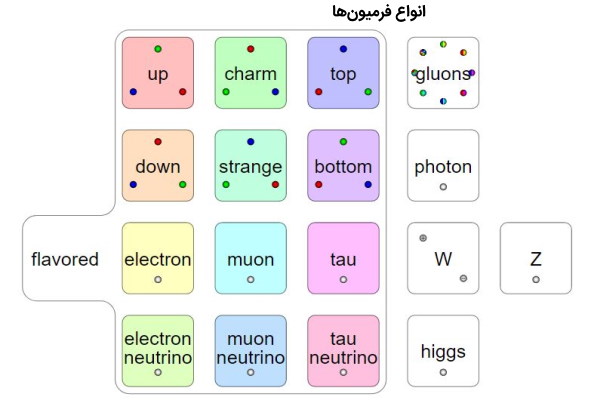
دوازده فرمیون وجود دارد که تفاوت بین آن‌ها نوع فرمیون است. کلمه flavor به معنای نوع استفاده شده است و فقط در مورد فرمیون‌ها کاربرد دارد. اما اگر دقت کنید flavor به معنی طعم و مزه است و چیزی است که در مورد ذرات زیراتمی قابل درک نیست. در حقیقت ذرات زیراتمی بسیار کوچک هستند و نمی‌توانند خصوصیاتی داشته باشند که مستقیماً توسط حواس انسان مشاهده شوند.

برهم کنش هسته‌ای ضعیف

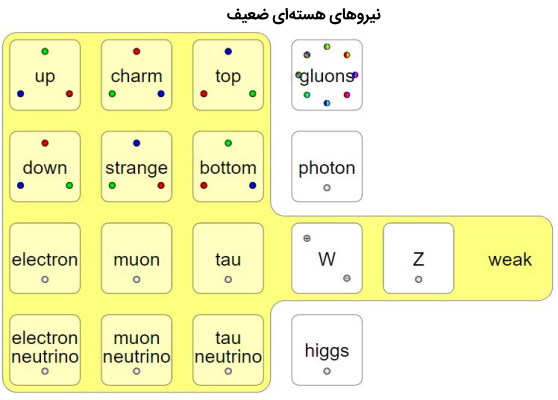
انواع ذرات از طریق تبادل بوزون W یا Z که حامل‌های نیروی ضعیف هستند و به عنوان بوزون‌های بردار میانی نیز شناخته می شوند با یکدیگر ارتباط ضعیفی دارند. در حقیقت هنگامی که یک نوترون یک پروتون تابش می‌کند یک بوزون $$W^{-}$$ مسئول است. مدل ریاضی که برای توصیف برهم کنش انواع فرمیون‌ها از طریق تبادل بوزون W و Z استفاده می‌شود به عنوان فلاوردینامیک کوانتومی (QFD) شناخته می‌شود، با این حال برخی از فیزیکدانان از این اصطلاح استفاده نمی‌کنند. در انرژی‌های بالاتر نیروهای ضعیف و الکترومغناطیسی بیشتر و بیشتر شبیه یکدیگر می‌شوند، مدل ریاضیاتی که این تعاملات را با هم توصیف می‌کند به عنوان نظریه الکتروضعیف (EWT) شناخته می‌شود. این نام برای توصیف ریاضیاتی نیروهای هسته‌ای ضعیف نیز استفاده می‌شود.

جرم و گرانش ذرات بنیادی

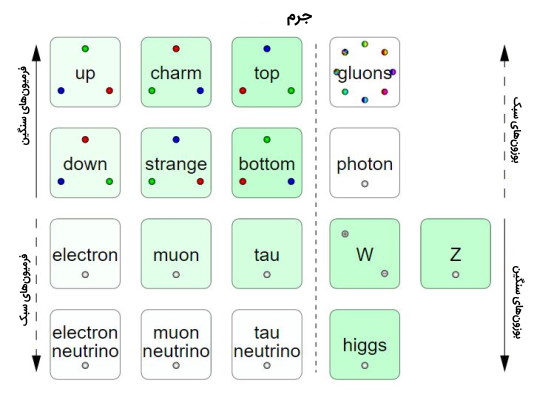
تصور می‌شود که تمام فرمیون‌ها دارای جرم سکون غیر صفر هستند. ذرات موجود در نسل I نسبت به نسل II از جرم کمتری برخوردار هستند و همچنین این ارتباط بین جرم ذرات موجود در نسل II و نسل III نیز وجود دارد. در طول نسل‌های مختلف کوارک‌ها جرم بیشتری نسبت به لپتون‌ها و نوترینوها جرم کمتری نسبت لپتون‌های دیگر دارند. وقتی صحبت از جرم می‌شود بوزون‌ها تقسیم می‌شوند، به این صورت که گلوئون‌ها و فوتون‌ها بدون جرم هستند در حالی که بوزون‌های W ،Z و هیگز جرم دارند.

جرم شکلی از انرژی است. یک ذره متحرک نسبت به ذره ثابت جرم بیشتری دارد زیرا دارای انرژی جنبشی است. از نظر منطقی یک ذره ثابت نباید جرمی داشته باشد. اگر بتوانیم یک فوتون را متوقف کنیم (که نمی‌توانیم) خواهیم دید که هیچ وزنی نخواهد داشت و به نظر می‌رسد منطق ما کار می‌کند. اما اگر یک الکترون را متوقف کنیم (که می‌توانیم) متوجه می‌شویم که وزن دارد و در این حالت منطق ما در مورد انرژی بودن جرم و صفر بودن جرم ذرات ساکن اشتباه خواهد بود. بدین ترتیب این سوال مطرح است که چرا بعضی از ذرات در حالت سکون وزن دارند و برخی دیگر هیچ وزنی ندارند؟

جرم شکلی از انرژی است و انرژی در دو نوع وجود دارد: انرژی جنبشی (انرژی حرکت) و انرژی پتانسیل (انرژی ساختار). سهم انرژی جنبشی در جرم جزئی است، بیشتر جرم اطراف ما از نوعی انرژی بالقوه حاصل می‌شود. به عنوان مثال یک پروتون از دو کوارک بالا و یک کوارک پایین ساخته شده است اما جرم این سه کوارک برابر با جرم یک پروتون نیست.

$$\large m_p\neq 2m_u+1m_d$$

$$\large 938.272 \mathrm{MeV} / \mathrm{c}^{2} \neq 2\left(2.3 \mathrm{MeV} / \mathrm{c}^{2}\right)+1\left(4.8 \mathrm{MeV} / \mathrm{c}^{2}\right)$$

$$\large 938.272 \mathrm{MeV} / \mathrm{c}^{2} \neq 9.4 \mathrm{MeV} / \mathrm{c}^{2}$$

جرم ذرات تشکیل دهنده پروتون فقط $$1\%$$ جرم کل ذره است. $$99\%$$ باقیمانده از انرژی پتانسیل نیروی قوی هسته‌ای نگهدارنده پروتون حاصل می‌شود. ذراتی که باعث ایجاد نیروی هسته‌ای قوی می‌شوند گلوئون‌ها هستند. انرژی برهم کنشی این ذرات بدون جرم همان چیزی است که بیشترین جرم را به پروتون می‌دهد.

سوالی که مطرح می‌شود این است که چرا کوارک‌ها جرم دارند اما گلوئون‌ها جرم ندارند؟ یا همانطور که این سوال از نظر تاریخی نیز بیان شد این است که چرا بوزون‌های W و Z جرم دارند اما فوتون اینگونه نیست؟ شاید نوع دیگری از انرژی پتانسیل وجود داشته باشد، یا شاید فعل و انفعال دیگری وجود داشته باشد. برهمکنشی که بعضی از ذرات احساس می‌کنند و برخی دیگر آن را احساس نمی‌کنند.

بدین ترتیب اگر چنین برهم کنشی وجود داشته باشد باید یک ذره وجود داشته باشد که در حالتی که ذرات بنیادی ساکن و بدون برهم کنش هستند به آن‌ها جرم دهد. نظریه برهم کنشی که به ذرات بنیادی جرم می‌دهد در سال 1964 توسط دانشمندان در سه مکان آکادمیک مستقل پیشنهاد شد، این سه گروه عبارت بودند از:

1. «فرانسوا انگلرت» (François Englert) و «رابرت بروت» (Robert Brout) در L'Université Libre de Bruxelles در بلژیک
2. «پیتر هیگز» (Peter Higgs) در دانشگاه ادینبورگ اسکاتلند
3. «جرالد گورالنیک» (Gerald Guralnik)، «کارل هاگن» (Carl Hagen) و «تام کیبل» (Tom Kibble) در کالج امپریال لندن

این ذره و این مکانیزم باید به نام Englert-Brout-Higgs-Guralnik-Hagen-Kibble نامیده شود اما به هر دلیلی اینطور نیست و برهم کنشی که به ذرات بنیادی جرم می‌دهد را مکانیزم هیگز و ذره‌ای که باعث جرم دار شدن ذرات بنیادی می‌شود را بوزون هیگز، ذره هیگز یا به ندرت هیگسون می‌نامند.

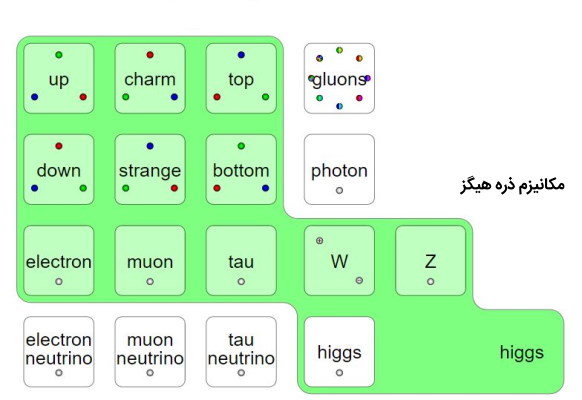
فرض بر این است که تمام فضا با یک میدان هیگز پر شده است. در حقیقت دریایی به عنوان پس زمینه از بوزون‌های هیگز مجازی وجود دارد که بین وجود و عدم وجود نوسان می‌کنند. کوارک‌ها، لپتون‌ها و بوزون‌های W و Z که در فضا به اطراف حرکت می‌کنند با این میدان برهم کنش دارند و به همین دلیل این ذرات دارای جرم هستند. فوتون‌ها و گلوئون‌ها با میدان هیگز برهم کنش ندارند و به همین دلیل این ذرات جرم ندارند.

حتی خود بوزون هیگز نیز با میدان هیگز برهم کنش می‌کند اما آیا به خودش جرم می‌دهد؟ بوزون هیگز با بوزون‌های دیگر یعنی گلوئون‌ها، فوتون‌ها و بوزون‌های W و Z متفاوت است زیرا نتیجه مکانیسم هیگز چیزی شبیه به نیروهایی مانند نیروهای هسته‌ای قوی، الکترومغناطیس و هسته‌ای ضعیف نمی‌شود. میدان هیگز یک میدان اسکالر و بوزون هیگز یک ذره با اسپین صفر است.

جاذبه نیروی بین اجسام به دلیل جرم آن‌ها است. مدل ریاضی که گرانش را روی سطح ذرات توصیف می‌کند گاهی اوقات هندسه دینامیک کوانتومی (QGD) نامیده می‌شود اما بیشتر اوقات به عنوان جاذبه کوانتومی نیز شناخته می‌شود. مدل استاندارد فیزیک ذرات گرانش را شامل نمی‌شود و در حال حاضر نظریه کوانتومی گرانش وجود ندارد. اگر وجود داشت باید یک نیرو برای حمل ذرات نیز وجود می‌داشت. نام پیشنهادی برای این ذره گراویتون است. نسبیت عام امواج گرانشی را به عنوان یک اختلال تانسوری توصیف می‌کند که منتشر می‌شوند و در امتداد دو جهت عمود متناوب فضا-زمان را قطع می‌کنند. این رفتار دو بعدی باعث می‌شود که فیزیکدانان نظری به این باور برسند که گراویتون اسپین دو دارد.

امید است که در نظریه‌ای فراتر از مدل استاندارد گرانش نیز در نظر گرفته شود. برخی از نظریه پردازان و تئوریسین‌ها باور دارند که چنین نظریه‌ای می‌تواند نظریه همه چیز یا Theory of everything باشد. با این حال تاریخ علم نشان داده است که هر چیزی گه ادعا می‌کند که نماینده‌ای از واقعیت نهایی است توسط نظریه‌ای بزرگتر و بهتر جایگزین می‌شود.

نظریه گروه مدل استاندارد ذرات

برای کسانی که ریاضیات پیشرفته را دوست دارند مدل استاندارد با استفاده از زبان نظریه گروه‌ها به صورت زیر بیان می‌شود:

$$\large \mathrm{SU}(3) \times \mathrm{SU}(2) \times \mathrm{U}(1)$$

در رابطه بالا پیمانه نیروهای هسته‌ای قوی با $$\mathrm{SU}(3)$$ و پیمانه نیروی‌های الکتروضعیف با $$\mathrm{SU}(2)\times\mathrm{U}(1)$$ نمایش داده می‌شود.

دقت داشته باشید که $$\mathrm{SU}(3)$$ ویژگی‌های زیر را دارا است:

• گروه واحد ویژه از مرتبه ۳
• مجموعه تمام ماتریس‌های $$3\times 3$$ واحد با دترمینان یک

همچنین $$\mathrm{SU}(2)$$ دارای ویژگی‌های زیر است:

• گروه واحد ویژه از مرتبه 2
• مجموعه تمام ماتریس‌های $$2\times 2$$ واحد با دترمینان یک
• نامتقارن با گروه چهارگانه با مقدار مطلق 1 $$\{x \in \mathbb{H}:|x|=1\}$$
• متفاوت با یک ابر کره
• همگن با گروه چرخش $$SO(3)$$ که مجموعه تمام چرخش‌های مربوط حول مرکز در فضای اقلیدسی سه بعدی معمولی است.

و در نهایت $$U(1)$$ نیز دارای ویژگی‌های زیر است:

• گروه واحد از مرتبه ۱
• مجموعه تمام ماتریس‌های واحد $$1\times 1$$
• نامتقارن با گروه دایره (گروه دایره یک گروه حاصلضرب اعداد مختلط با مقدار مطلق 1 است یعنی: $$\mathrm{T}=\{x \in C:|x|=1\}$$)
• نامتقارن با گروه $$SO(2)$$، یک گروه متعامد ویژه مرتبه دوم

جمع‌بندی

در این مطلب در مورد ذرات بنیادی و مدل استاندارد صحبت کردیم. بر اساس مدل استاندارد ۶ ذره حامل ماده و پنج ذره حامل انرژی هستند که با در نظر گرفتن گراویتون تعداد حامل‌های انرژی در مدل استاندارد ۶ ذره است (گلوئون، فوتون، Z، $$W^{-}$$، $$W^{+}$$ و هیگز).

همچنین در مورد نیرو‌های حاکم بر ذرات بنیادی در مدل استاندارد ذرات صحبت کردیم و نشان دادیم دلیل هر یک از نیروها در ذرات بنیادی به دلیل وجود مشخصه‌ای در ذرات است. در ادامه پیمانه فعل و انفعالات هر نیرو را نیز معرفی کردیم. در نهایت توضیح دادیم که چرا برخی از ذرات جرم دارند و برخی فاقد جرم هستند.