مجموع زوایای داخلی ذوزنقه چقدر است؟ + حل تمرین و مثال

مجموع زوایای داخلی ذوزنقه برابر با 360 درجه است. اما این مجموع چگونه به دست می‌آید. در این مقاله، فرمول و نحوه محاسبه مجموع زوایای داخلی ذوزنقه را به همراه حل چندین مثال متنوع آموزش می‌دهیم. به علاوه، نحوه بدست آوردن مجموع زوایای داخلی ذوزنقه برای حالت‌های خاص (قائم الزاویه و متساوی الساقین) را نیز بررسی می‌کنیم.

ذوزنقه چیست ؟

ذوزنقه چهار ضلعی‌ای است که حداقل دو ضلع آن با هم موازی هستند. تصویر زیر مثال‌های مختلف ذوزنقه را نمایش می‌دهد. به ضلع‌های موازی، قاعده ذوزنقه و به ضلع‌های غیر موازی، ساق ذوزنقه می‌گویند.

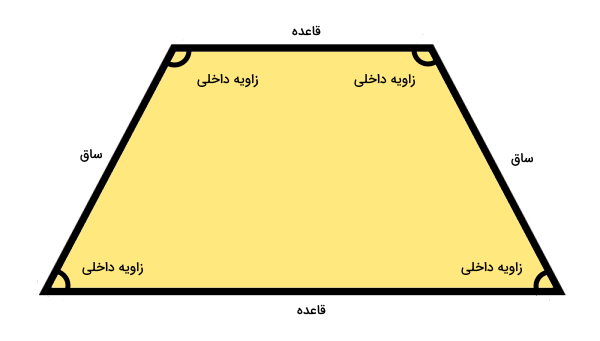
از ویژگی‌های ذوزنقه می‌توان به موارد زیر اشاره کرد:

• دو تا از ضلع‌های ذوزنقه همیشه با هم موازی‌اند.
• ذوزنقه گاهی دو زاویه راست دارد (ذوزنقه قائم الزاویه).
• ذوزنقه گاهی دو ساق برابر دارد (ذوزنقه متساوی الساقین).
• دو زاویه هر ساق ذوزنقه همیشه مکمل یکدیگر هستند (مجموع آن‌ها برابر 180 درجه است).

در ذوزنقه متساوی الساقین، زوایای داخلی مجاور به هر قاعده با هم برابر هستند.

زاویه داخلی چیست ؟

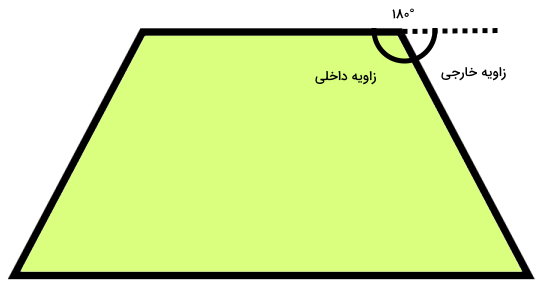
زاویه داخلی، زاویه بین ضلع‌های مجاور یک چند ضلعی است که درون محیط آن قرار می‌گیرد. تصویر زیر، ارتباط بین یکی از زوایای داخلی و خارجی ذوزنقه را نمایش می‌دهد.

مجموع زوایای داخلی اشکال هندسی چگونه بدست می آید ؟

مجموع زوایای داخلی اشکال هندسی، بر اساس تعداد ضلع‌های آن به دست می‌آید. در ادامه، مجموع زوایای داخلی برخی از چند ضلعی‌ها آورده شده است:

• مجموع زوایای داخلی سه ضلعی (مثلث): 180 درجه
• مجموع زوایای داخلی چهار ضلعی (مربع، لوزی، مستطیل و غیره): 360 درجه
• مجموع زوایای داخلی پنج ضلعی: 540 درجه
• مجموع زوایای داخلی شش ضلعی: 720 درجه

رابطه جبری بین تعداد ضلع‌های چند ضلعی و مجموع زوایای داخلی آن به صورت زیر نوشته می‌شود:

$$S = (n-2) \times180°$$

• S: مجموع زوایای داخلی
• n: تعداد ضلع‌ها

مجموع زاویه داخلی ذوزنقه چقدر است ؟

مجموع زوایای داخلی ذوزنقه برابر 360 درجه است. ذوزنقه، یک چهار ضلعی با دو ضلع موازی و دو ضلع غیر موازی محسوب می‌شود. بر اساس فرمول مجموع زوایای داخلی، داریم:

$$S = (n-2) \times 180°$$

• S: مجموع زوایای داخلی ذوزنقه
• n: تعداد ضلع‌ها برابر 4

$$S = (4-2) \times180°$$

$$S = (2) \times 180°$$

$$S = 360°$$

تصویر زیر، یک ذوزنقه و زوایای داخلی آن را نمایش می‌دهد.

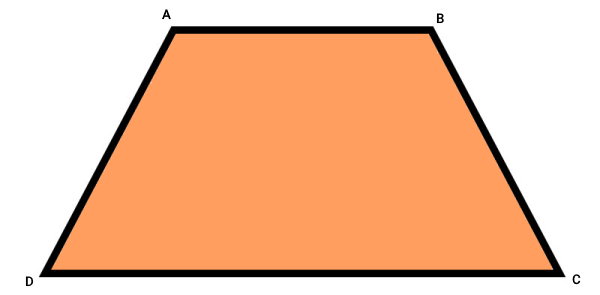
مجموع زوایای داخلی ذوزنقه بالا برابر است با:

360° = زاویه چهارم + زاویه سوم + زاویه دوم + زاویه اول

360° = A + B + C + D

مجموع زوایای خارجی ذوزنقه چقدر است ؟

مجموع زوایای داخلی ذوزنقه برابر 360 است. در واقع، مجموع زوایای خارجی تمام چندضلعی‌ها برابر با 360 خواهد بود.

مجموع زاویه داخلی و خارجی ذوزنقه چقدر است ؟

جمع زاویه داخلی یک راس ذوزنقه با زاویه خارجی همان راس، برابر 180 درجه است. قانون جمع زوایای داخلی و خارجی راس‌ها، برای تمام چند ضلعی‌ها صدق می‌کند.

مثال های مجموع زوایای داخلی ذوزنقه

در این بخش، چند مثال متنوع را در زمینه محاسبه مجموع زوایای داخلی ذوزنقه حل می‌کنیم.

مثال 1: تعیین اندازه زاویه و نوع ذوزنقه از روی مجموع زوایای داخلی

مجموع سه زاویه داخلی یک ذوزنقه برابر 270 درجه است. اندازه زاویه چهارم و نوع ذوزنقه را مشخص کنید.

به منظور محاسبه زاویه چهارم، از مجموع زوایای داخلی استفاده می‌کنیم. رابطه مجموع زوایای داخلی ذوزنقه به صورت زیر نوشته می‌شود:

360° = زاویه چهارم + زاویه سوم + زاویه دوم + زاویه اول

با توجه به صورت سوال، مجموع سه زاویه ذوزنقه، برابر با 270 درجه است. این عدد را به جای سه زاویه در رابطه بالا قرار می‌دهیم:

360° = زاویه چهارم + °270

90° = زاویه چهارم

زاویه چهارم ذوزنقه برابر 90 درجه است. در نتیجه، این ذوزنقه از نوع قائم الزاویه است.

مثال 2: محاسبه مجموع سه زاویه ذوزنقه

یکی از زوایای ذوزنقه نمایش داده شده در تصویر زیر برابر 100 درجه است. مجموع سه زاویه دیگر آن را پیدا کنید.

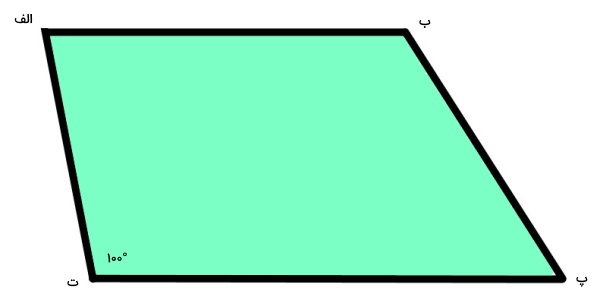
برای این مثال، مجموع زوایای ذوزنقه را می‌توان به صورت زیر نوشت:

360° = زاویه ت + مجموع سه زاویه

360° = 100° + مجموع سه زاویه

100° - 360° = مجموع سه زاویه

260° = مجموع سه زاویه

مجموع سه زاویه دیگر ذوزنقه برابر 260 درجه است.

مثال 3: تعیین تمام زوایای داخلی ذوزنقه قائم الزاویه

یکی از زوایای یک ذوزنقه قائم الزاویه برابر 70 درجه است. اندازه سه زاویه دیگر آن را حساب کنید.

ذوزنقه قائم الزاویه دارای دو زاویه راست یا 90 درجه است. با توجه به اطلاعات مسئله شکل کلی این ذوزنقه به صورت زیر خواهد بود.

مجموع زوایای داخلی ذوزنقه بالا عبارت است از:

$$A + B + C + D = 360°$$

$$90° + 90° + 70° + D = 360°$$

$$250° - D = 360°$$

$$D = 110°$$

زاویه چهارم ذوزنقه برابر 110 درجه است.

مثال 4: تعیین مجموع زوایای داخلی ذوزنقه متساوی الساقین

اندازه دو زاویه یک ذوزنقه متساوی الساقین برابر 60 درجه است. اندازه دو زاویه دیگر این ذوزنقه را حساب کنید.

در ذوزنقه متساوی الساقین، چهار زاویه داخلی، دو به دو با هم برابر هستند. تصویر زیر، شکل کلی ذوزنقه این مثال را نمایش می‌دهد.

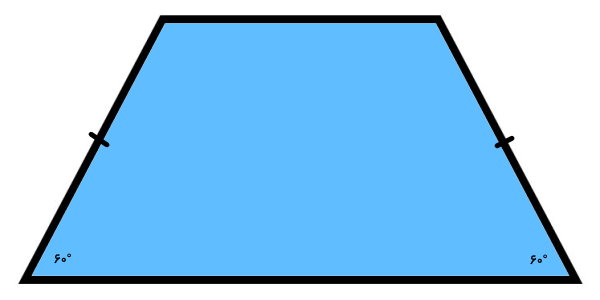
بر اساس رابطه مجموع زوایای ذوزنقه، داریم:

$$A + B + C + D = 360°$$

زوایای A و B، مجاور با یکی از قاعده‌ها و برابر با 60 درجه هستند. این مقادیر را درون رابطه بالا قرار می‌دهیم:

$$60° + 60° + C + D = 360°$$

$$120° + C + D = 360°$$

$$C + D = 360° - 120°$$

$$C + D = 240°$$

مجموع دو زاویه دیگر ذوزنقه برابر 240 درجه است. از آنجایی که این دو زاویه، مجاور با قاعده دیگر ذوزنقه هستند، اندازه آن‌ها با هم برابر خواهد بود. در نتیجه:

$$C = 120°$$

$$D = 120°$$

مثال 5: مجموع زوایای داخلی مثلث های درون ذوزنقه

تصویر زیر، ذوزنقه‌ای را نمایش می‌دهد که با رسم یک پاره خط از دو راس مقابل آن، به دو مثلث تبدیل شده است. مجموع زوایای داخلی این دو مثلث را تعیین و مقدار به دست آمده را با مجموع زوایای داخلی ذوزنقه مقایسه کنید. از این مثال چه نتیجه‌ای می‌گیرید؟

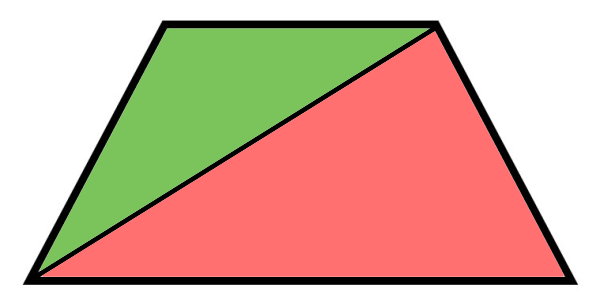
مجموع زوایای داخلی مثلث برابر 180 درجه است. این مقدار از رابطه زیر به دست می‌آید:

$$S = (n-2) \times180°$$

• S: مجموع زوایای داخلی مثلث
• n: تعداد ضلع‌های مثلث برابر 3

$$S = (3-2) \times180°$$

$$S = (1) \times 180°$$

$$S = 180°$$

در نتیجه مجموع دو مثلث تشکیل ذوزنقه برابر است با:

$$180° + 180° = 360°$$

مجموع زوایای داخلی دو مثلث با مجموع زوایای داخلی ذوزنقه برابر شد. از این مثال می‌توان نتیجه گرفت که مجموع زوایای داخلی هر چند ضلعی، برابر با مجموع زوایای داخلی مثلث‌های تشکیل‌دهنده آن‌ها است؛ به شرطی که ضلع‌های این مثلث‌ها از مبدا یکی از راس‌های ذوزنقه رسم شده و همدیگر را قطع نکرده باشند.

مثال 6: زوایای خارجی و مجموع زوایای خارجی ذوزنقه

تصویر زیر، یک ذوزنقه با دو زاویه داخلی معلوم را نمایش می‌دهد. اندازه زاویه داخلی چهارم، هر یک از زوایای خارجی و مجموع زوایای خارجی ذوزنقه را حساب کنید.

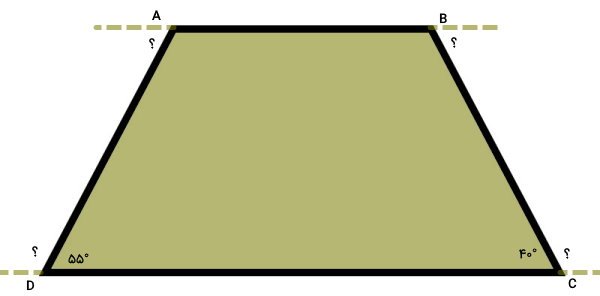
در ذوزنقه بالا، زوایای داخلی C و D معلوم هستند. می‌دانیم که مجموع دو زاویه داخلی متصل به هر ساق برابر 180 درجه است. با توجه به این نکته، زاویه A به صورت زیر تعیین می‌شود:

$$A + D = 180°$$

$$A + 55° = 180°$$

$$A = 180° - 55°$$

$$A = 125°$$

زاویه B نیز به همین صورت به دست می‌آید:

$$B + C = 180°$$

$$B + 40° = 180°$$

$$B = 180° - 40°$$

$$B = 140°$$

اکنون می‌توانیم تمام زوایای خارجی ذوزنقه را بدست بیاوریم. مجموع زوایای داخلی و خارجی هر راس برابر با 180 درجه است. از این‌رو، زوایای خارجی راس‌های A تا D، به ترتیب برابر خواهند بود با:

$$180° - 125° = 55°$$

$$180° - 140° = 40°$$

$$180° - 40° = 140°$$

$$180° - 55° = 125°$$

مجموع زوایای خارجی نیز برابر است با:

$$55° + 40° + 140° + 125° = 360°$$

همان طور که مشاهده می‌کنید، مجموع زوایای خارجی ذوزنقه مانند تمام چند ضلعی‌ها برابر 360 درجه است.

سوالات متداول مجموع زاویه های داخلی ذوزنقه

در این بخش، به برخی از سوالات پرتکرار در رابطه با مجموع زوایای داخلی ذوزنقه پاسخ می‌دهیم.

ذوزنقه چند زاویه داخلی دارد؟

ذوزنقه یکی از اشکال هندسی چند ضلعی است که چهار ضلع و چهار زاویه داخلی دارد.

مجموع زاویه های داخلی ذوزنقه چند درجه است ؟

مجموع زوایای داخلی ذوزنقه برابر 360 درجه است.

مجموع زاویه های خارجی ذوزنقه چند درجه است ؟

مجموع زوایای خارجی ذوزنقه برابر 360 درجه است.

فرمول مجموع زاویه های داخلی ذوزنقه چیست؟

فرمول مجموع زوایای داخلی ذوزنقه برابر °180×(n-2) است که در آن، n، تعداد ضلع‌های ذوزنقه را نمایش می‌دهد.