مجموعه محدب چیست؟ — راهنمای جامع

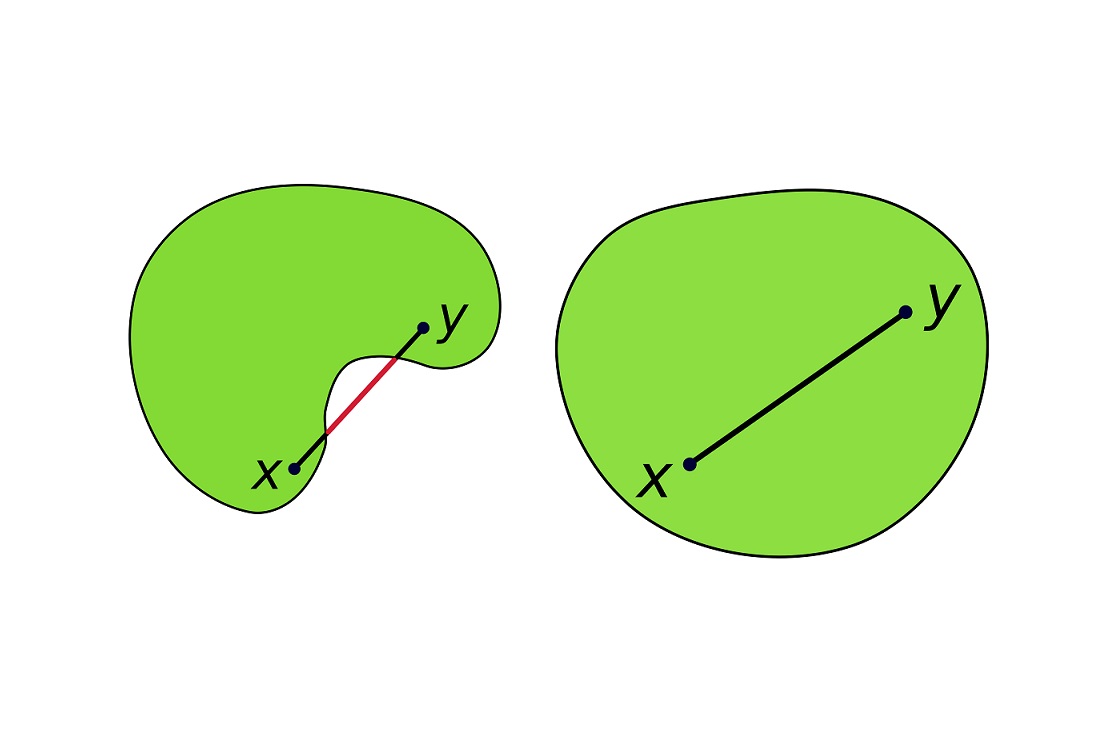
یک «مجموعه محدب» (Convex Set) به مجموعه‌ای از نقاط گفته می‌شود که خط AB که هر دو نقطه فرضی A و B در این مجموعه را به هم متصل می‌کند، به صورت کامل درون مجموعه قرار داشته باشد. به صورت شهودی این امر بدین معنا است که مجموعه «متصل» (Connected) است، بنابراین می‌توان از هر دو نقطه از مجموعه چنان گذر کرد که لازم نباشد از مجموعه خارج شد. در یک مجموعه محدب هیچ دندانه و فرورفتگی در فضای احاطه کننده وجود ندارد. بخش‌های محیط بیرونی ممکن است خطوط راست باشند. در این مطلب قصد داریم به بیان تعریف مجموعه محدب بپردازیم و چند مثال از مجموعه‌های محدب را به صورت ریاضی اثبات کنیم.

تعریف مجموعه محدب

فرض کنید که $$ S \subseteq \mathbb { R } ^ n $$ باشد. یک مجموعه S را محدب می‌گویند اگر خط متصل کننده هر دو نقطه در مجموعه S، خود نیز به مجموعه S تعلق داشته باشد. به عبارت دیگر، اگر $$ x _ 1 , x _ 2 \in S $$ باشند، آن‌گاه $$ \lambda x _ 1 + \left ( 1 - \lambda \right ) x _ 2 \in S $$ نیز صادق باشد که در این رابطه $$ \lambda \in \left ( 0 , 1 \right ) $$ است.

فیلم آموزش کنترل بهینه در فرادرس

کلیک کنید

در تصویر زیر نمایی از یک مجموعه محدب نشان داده شده است.

نکته

1. اجتماع دو مجموعه محدب، ممکن است یک مجموعه محدب باشد یا نباشد.
2. اشتراک دو مجموعه محدب همواره یک مجموعه محدب است.

اثبات

فرض کنید $$ S _ 1 $$ و $$ S _ 2 $$ دو مجموعه محدب باشند. مجموعه $$ S _ 3 = S _ 1 \cap S _ 2 $$ را در نظر می‌گیریم به نحوی که $$ x _ 1 , x _ 2 \in S _ 3 $$ باشند. چون $$ S _ 3 = S _ 1 \cap S _ 2 $$ است، در نتیجه $$ x _ 1 , x _ 2 \in S _ 1 $$ و $$ x _ 1 , x _ 2 \in S _ 2 $$ صادق هستند. چون به ازای هر $$ i \in 1 , 2 $$، مجموعه $$ S _ i $$ یک مجموعه محدب است، در نتیجه $$ \lambda x _ 1 + \left ( 1 - \lambda \right ) x _ 2 \in S _ i $$ است که در آن $$ \lambda \in \left ( 0 , 1 \right ) $$ فرض شده است. از این می‌توان نتیجه گرفت $$ \lambda x _ 1 + \left ( 1 - \lambda \right ) x _ 2 \in S _ 1 \cap S _ 2 $$ است و بنابراین $$ \lambda x _ 1 + \left ( 1 - \lambda \right ) x _ 2 \in S _ 3  $$ صادق است. به همین دلیل می‌توان گفت که $$ S _ 3 $$ که اشتراک دو مجموعه محدب است، خود یک مجموعه محدب به شمار می‌آید.

در ادامه می‌خواهیم چند تعریف که در مجموعه‌های محدب متداول است را بررسی کنیم.

ترکیب مخروطی (Conic Combination): میانگین وزن‌دار به فرم $$ \displaystyle \sum \limits _ { i = 1 } ^ k \lambda _ i x _ i $$ که در آن $$ \displaystyle \sum \limits _ { i = 1 } ^ k \lambda _ i = 1 $$ و $$ \lambda _ i \geq 0 , \forall i \in \left [ 1 , k \right ] $$ باشد، یک ترکیب مخروطی از $$ x _ 1 , x _ 2 , . . . . x _ k $$ نام دارد.

ترکیب افاین (Affine Combination): میانگین وزن‌دار به فرم $$ \displaystyle \sum \limits _ { i = 1 } ^ k \lambda _ i x _ i $$ را یک ترکیب افاین از $$ x _ 1 , x _ 2 , . . . . x _ k $$ می‌گویند که در آن $$ \displaystyle \sum \limits _ { i = 1 } ^ k \lambda _ i = 1 $$ است.

ترکیب خطی (Linear Combination): میانگین وزن‌دار به فرم $$ \displaystyle \sum \limits _ { i = 1 } ^ k \lambda _ i x _ i $$، یک ترکیب خطی از $$ x _ 1 , x _ 2 , . . . . x _ k $$ نام دارد.

مثال ۱

ثابت کنید که مجموعه $$ S = \left \{ x \in \mathbb { R } ^ n : C x \leq \alpha \right \} $$ یک مجموعه محدب است.

حل

فرض کنید $$ x _ 1 $$ و $$ x _ 2 $$ عضو مجموعه $$ S $$ باشند. آن‌گاه می‌توان نوشت $$ C x _ 1 \leq \alpha $$ و $$ C x _ 2 \leq \alpha $$. برای اثبات این سوال می‌توانیم به طریق زیر عمل کنیم:

$$ y = \left ( \lambda x _ 1 + \left ( 1 - \lambda \right ) x _ 2 \right ) \in S \: \forall \: \lambda \in \left ( 0 , 1 \right ) $$

حال $$ C $$ را در دو طرف معادله ضرب می‌کنیم:

$$ C y = C \left ( \lambda x _ 1 + \left ( 1 - \lambda \right ) x _ 2 \right ) = \lambda C x _ 1 + \left ( 1 - \lambda \right ) C x _ 2 $$

نتیجه را می‌توان به صورت زیر بازنویسی کرد:

$$ \Rightarrow C y \leq \lambda \alpha + \left ( 1 - \lambda \right ) \alpha $$

$$ \Rightarrow C y \leq \alpha $$

در نتیجه $$ y\in S $$ است و اثبات شد که $$ S $$ یک مجموعه محدب است.

مثال ۲

اثبات کنید که مجموعه $$ S = \left \{ \left ( x _ 1 , x _ 2 \right ) \in \mathbb { R } ^ 2 : x _ { 1 } ^ { 2 } \leq 8 x _ 2 \right \} $$ یک مجموعه محدب به شمار می‌آید.

حل

فرض کنید $$ x , y \in S $$ باشد. حال دو مجموعه $$ x = \left ( x _ 1 , x _ 2 \right ) $$ و $$ y = \left ( y _ 1 , y _ 2 \right ) $$ را تعریف می‌کنیم. بنابراین می‌توانیم بنویسیم که $$ x _ { 1 } ^ { 2 } \leq 8 x _ 2 $$ و $$ y _ { 1 } ^ { 2 } \leq 8 y _ 2 $$ است. برای اثبات این سوال نیز همانند سوال قبل عمل می‌کنیم و شرط محدب بودن را می‌نویسیم:

$$ \lambda x + \left ( 1 - \lambda \right ) y \in S \\
\Rightarrow \lambda \left ( x _ 1 , x _ 2 \right ) + \left ( 1 -\lambda \right ) \left ( y _ 1 , y _ 2 \right ) \in S \\
\Rightarrow \left [ \lambda x _ 1 + \left ( 1 - \lambda) y _ 1 ] \in S \right ) \right ] $$

حال رابطه را به توان دو می‌رسانیم:

$$ \left [ \lambda x _ 1 + \left ( 1 - \lambda \right ) y _ 1 \right ] ^ { 2 } = \lambda ^ 2 x _ { 1 } ^ { 2 } + \left ( 1 - \lambda \right ) ^ 2 y _ { 1 } ^ { 2 } + 2 \lambda \left ( 1 - \lambda \right ) x _ 1 y _ 1 $$

رابطه $$ 2 x _ 1 y _ 1 \leq x _ { 1 } ^ { 2 } + y _ { 1 } ^ { 2 } $$ صحیح است، بنابراین داریم:

$$ \left [ \lambda x _ 1 + \left ( 1 - \lambda \right ) y _ 1 \right ] ^ { 2 } \leq \lambda ^ 2 x _ { 1 } ^ { 2 } + \left ( 1 - \lambda \right ) ^ 2 y _ { 1 } ^ { 2 } + 2 \lambda \left ( 1 - \lambda \right ) \left ( x _ { 1 } ^ { 2 } + y _ { 1 } ^ { 2 } \right ) $$

با توجه به رابطه فوق، رابطه زیر نیز صحیح است:

$$ \Rightarrow \left [ \lambda x _ 1 + \left ( 1 - \lambda \right ) y _ 1 \right ] ^ { 2 } \leq \lambda x _ { 1 } ^ { 2 } + \left ( 1 - \lambda \right ) y _ { 1 } ^ { 2 } $$

حال اگر طرف دوم رابطه را در ۸ ضرب کنیم و توان دوم را نیز حذف کنیم، رابطه باز هم صادق است:

$$ \Rightarrow \left [ \lambda x _ 1 + \left ( 1 - \lambda \right ) y _ 1 \right ] ^ { 2 } \leq 8 \lambda x _ 2 + 8 \left ( 1 - \lambda \right ) y _ 2 $$

از عدد ثابت ۸ فاکتور می‌گیریم:

$$ \Rightarrow \left [ \lambda x _ 1 + \left ( 1 - \lambda \right ) y _ 1 \right ] ^ { 2 } \leq 8 \left [ \lambda x _ 2 + \left ( 1 - \lambda \right ) y _ 2 \right ] $$

با توجه به رابطه فوق، اثبات شد که $$ \lambda x + \left ( 1 - \lambda \right ) y \in S  $$ صادق است و در نتیجه این مجموعه، یک مجموعه محدب است.

مثال ۳

اثبات کنید که مجموعه $$ S \in \mathbb { R } ^ n $$ یک مجموعه محدب است اگر و فقط اگر برای هر عدد صحیح K، هر ترکیب محدب از نقاط K مربوط به $$ S $$ نیز در $$ S $$ قرار داشته باشد.

حل

فرض کنید $$ S $$ یک مجموعه محدب باشد، در این صورت باید ثابت کنیم که به ازای $$ \forall i \in 1 , 2 , . . . . , k  $$ و $$ c _ i \geq 0 $$ روابط زیر صحیح هستند:

$$ c _ 1 x _ 1 + c _ 2 x _ 2 + . . . . . + c _ k x _ k \in S $$

$$ \displaystyle \sum \limits _ { 1 } ^ k c _ i = 1 $$

حال می‌توانیم به روش استقرایی این سوال را اثبات کنیم. به ازای $$ k = 1 , x _ 1 \in S , c _ 1 = 1 $$ داریم:

$$ c _ 1 x _ 1 \in S $$

به ازای $$ k = 2 , x _ 1 , x _ 2 \in S $$ نیز رابطه $$ c _ 1 + c _ 2 = 1 $$ صحیح است و چون $$ S $$ یک مجموعه محدب است، در نتیجه داریم:

$$ c _ 1 x _ 1 + c _ 2 x _ 2 \in S $$

فرض کنید ترکیب محدب نقاط m از مجموعه $$ S $$ در مجموعه $$ S $$ باشد. به عبارت دیگر می‌توان نوشت:

$$ c _ 1 x _ 1 + c _ 2 x _ 2 + . . . + c _ m x _ m \in S , \displaystyle \sum \limits _ { 1 } ^ m c _ i = 1 , c _ i \geq 0 , \forall i \in 1 , 2 , . . . , m $$

حال فرض کنید $$ x _ 1 , x _ 2 . . . . , x _ m , x _ { m + 1 } \in S $$ باشد. متغیر $$ x = \mu _ 1 x _ 1 + \mu _ 2 x _ 2 + . . . + \mu _ m x _ m + \mu _ { m + 1 } x _ { m + 1 } $$ را در نظر بگیرید. این متغیر را به دو بخش می‌شکنیم و بخش اول را در کسر $$ \frac { \mu _ 1 x _ 1 + \mu _ 2 x _ 2 + . . . + \mu _ m x _ m } { \mu _ 1 + \mu _ 2 + . . . . . . . . . + \mu _ m } $$ ضرب می‌کنیم. در نتیجه داریم:

$$ x = \left ( \mu _ 1 + \mu _ 2 + . . . + \mu _ m \right ) \frac { \mu _ 1 x _ 1 + \mu _ 2 x _ 2 + \mu _ m x _ m }{ \mu _ 1 + \mu _ 2 + . . . . . . . . . + \mu _ m } + \mu _ { m + 1 } x _ { m + 1 } $$

متغیر $$ y = \frac { \mu _ 1 x _ 1 + \mu _ 2 x _ 2 + . . . + \mu _ m x _ m } { \mu _ 1 + \mu _ 2 + . . . . . . . . . + \mu _ m } $$ را در معادله جایگذاری می‌کنیم. نتیجه به صورت زیر نوشته می‌شود:

$$ x = \left ( \mu _ 1 + \mu _ 2 + . . . + \mu _ m \right ) y + \mu _ { m + 1 } x _ { m + 1 } $$

حال می‌توان گفت $$ y \in S $$ است؛ زیرا مجموع ضرایب برابر با یک در نظر گرفته می‌شود. در نتیجه $$ x \in S $$ است چون $$ S $$ یک مجموعه محدب است و $$ y , x _ { m + 1 } \in S $$. بنابراین سوال به صورت استقرایی اثبات شد.

اگر این مطلب برای شما مفید بوده است و به یادگیری بیشتر در این زمینه علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• توابع محدب و مقعر — از صفر تا صد
• بهینه سازی چند هدفه چیست؟ — راهنمای جامع
• عدد اصلی مجموعه یا کاردینالیتی — به زبان ساده
• مجموعه فازی (Fuzzy Set) — به زبان ساده

^^