قضیه میلر – از صفر تا صد (+ دانلود فیلم آموزش رایگان)
قضیه میلر به فرایند معادلسازی بخشی از یک مدار الکتریکی اشاره میکند. در این مطلب قصد داریم به بیان این قضیه و نیز دوگان قضیه آن بپردازیم و کاربردهای آنها را شرح دهیم.
فیلم آموزشی قضیه میلر
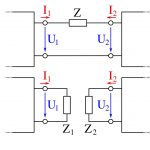
ثابت میشود که یک المان با امپدانس شناور، که به دو پورت آن دو منبع ولتاژ به صورت سری متصل شده است، میتواند به دو المان با امپدانس متناظر تجزیه شود که این المانهای متناظر به زمین متصل شدهاند. همچنین قضیه دوگان میلر نیز وجود دارد، که برای معادلسازی امپدانسهایی که با منابع جریان تغذیه شدهاند، بکار میرود. هر دو قضیه بر پایه قوانین تحلیل مدارهای الکتریکی با استفاده از KCL و KVL یا کیرشهف استوار هستند.
قضیه میلر فقط یک بیان ریاضی محض نیست. این تئوری پدیدههای مهم مداری درباره اصلاح امپدانس (اثر میلر، زمین مجازی، امپدانس منفی و ...) را توضیح میدهد. علاوه بر این، منجر به طراحی راحتتر و درک بهتر مدارات متداول (تقویتکننده فیدبک، مقاومتها و مبدلهای وابسته به زمان و مبدلهای با امپدانس منفی) میشود. این قضیه در آنالیز مداراتی که دارای فیدبک هستند، کاربرد ویژهای دارد. همچنین برای تحلیل برخی تقویتکنندههای ترانزیستوری در فرکانسهای بالا کاربردهای فراوانی دارد.
بین قضیه میلر و اثر میلر ارتباطی نزدیک وجود دارد. قضیه میلر را میتوان به صورت فرم تعمیم یافته اثر میلر در نظر گرفت و همچنین اثر میلر را میتوان به عنوان حالتی خاصی از قضیه میلر در نظر گرفت.
قضیه میلر برای ولتاژ
قضیه میلر بیان میکند که در یک مدار خطی، اگر شاخهای با امپدانس Z وجود داشته باشد که دو گره با ولتاژهای و را به یکدیگر متصل کند، آنگاه میتوان این شاخه را با دو شاخه دیگر جایگزین کرد، که این شاخهها گرههای متناظر را از طریق امپدانسهای و به زمین متصل میکنند.
قضیه میلر را میتوان با استفاده از تکنیک شبکههای دو قطبی و اعمال قضیه جذب منبع (Source Absorption) اثبات کرد. این حالت قضیه میلر بر اساس قانون ولتاژ کیرشهف است و به همین دلیل قضیه میلر برای ولتاژ نیز نام دارد. تصویر زیر اعمال قضیه میلر برای حذف امپدانس مستقیم بین دو گره 1 و 2 را به صورت شماتیکی نشان میدهد.
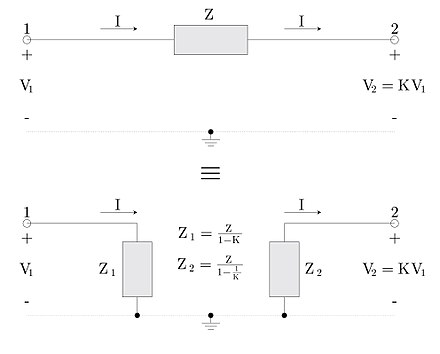
شرح قضیه میلر
قضیه میلر در رابطه با یک امپدانس است که توسط دو منبع ولتاژ دلخواه (نه لزوما وابسته) تغذیه میشود. این منابع ولتاژ از طریق زمین مشترک خود به صورت سری به یکدیگر متصل میشوند. یکی از منابع ولتاژ، به عنوان منبع ولتاژ اصلی (مستقل) با ولتاژ و دیگری به عنوان یک منبع ولتاژ اضافی عمل میکنند. منبع ولتاژ دوم به صورت خطی وابسته به ولتاژ منبع اول است و مقدار آن برابر با است. ایده اصلی قضیه میلر (اصلاح امپدانس دیده شده از طرفین منابع ورودی و خروجی) از طریق مقایسه دو حالت اتصال به منبع ولتاژ اضافی و بدون اتصال به منبع ولتاژ اضافی به دست آمده است.
اگر ولتاژ برابر با صفر باشد (منبع ولتاژ دوم وجود نداشته باشد، یا سمت راست المان با امپدانس Z به زمین متصل باشد.)، جریان ورودی جاری در المان، بر اساس قانون اهم و تنها با کمک ولتاژ به صورت زیر به دست میآید:
امپدانس ورودی مدار نیز برابر است با:
چون مدار شامل یک منبع ولتاژ دوم نیز هست، جریان ورودی به هر دو ولتاژ بستگی دارد. بر حسب پلاریته منبع ولتاژ، ولتاژ یا به ولتاژ اضافه میشود و یا از آن کم میشود. بنابراین جریان ورودی یا اضافه یا کم میشود.
امپدانس ورودی مدار که از سمت منبع ورودی دیده میشود نیز به صورت متناظر افزایش یا کاهش مییابد.
بنابراین میتوان گفت قضیه میلر این حقیقت را بیان میکند که اتصال یک منبع ولتاژ دوم با مقدار نسبی به صورت سری با منبع ولتاژ ورودی، باعث تغییر در ولتاژ موثر و جریان میشود و به صورت متناظر امپدانس مدار دیده شده از سمت منبع ورودی نیز تغییر میکند. بسته به پلاریته، مانند یک منبع ولتاژ مکمل عمل میکند که یا به منبع ولتاژ اصلی برای عبور دادن جریان از امپدانس کمک و یا با آن مخالفت میکند.
از طرف دیگر، با معادل کردن ترکیب دو منبع ولتاژ به عنوان یک منبع ولتاژ ترکیبی، میتوان قضیه میلر را اینطور توضیح داد که با ترکیب المان واقعی و منبع ولتاژ دوم، یک عنصر مجازی جدید با امپدانس دینامیکی اصلاح شده به دست میآید. از این نظر، یک ولتاژ اضافی است که به صورت مصنوعی افت ولتاژ در طول امپدانس Z را افزایش یا کاهش میدهد. نسبت بین ولتاژها، مقدار امپدانس اصلاح شده را مشخص میکند و در شش گروه طبقهبندی انجام میگیرد.
تفریق از
| مقایسه و | ||||
| منفی با جریان معکوس | بینهایت | افزایش یافته | عادی | امپدانس |
جمع با
| مقایسه و | ||||
| منفی با ولتاژ معکوس | صفر | کاهش یافته | عادی | امپدانس |
اگر جای ولتاژهای و عوض شود و نیز ضریب با جایگزین شود، امپدانس مدار دیده شده از سمت منبع خروجی نیز، میتواند به صورت مشابه تعریف شود.
پیادهسازی قضیه میلر با استفاده از تقویتکننده ولتاژ
قضیه میلر غالبا توسط آرایشی متشکل از یک المان با امپدانس پیادهسازی میشود. این المان بین دو ترمینال یک شبکه خطی قرار دارد و به زمین متصل است. معمولا یک تقویتکننده ولتاژ با بهره به عنوان چنین شبکه خطی در نظر گرفته میشود، اما المانهای دیگری نیز میتوانند این نقش را بازی کنند؛ مثلا یک پتانسیومتر یا انتگرالگیر الکترومکانیکی (یک سرومکانیزم با استفاده از سنسور فیدبک پتانسیومتری). شکل زیر نمایی از یک پیادهسازی متداول قضیه میلر بر اساس تقویتکننده ولتاژ را نشان میدهد.
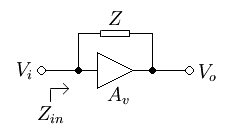
در پیادهسازی قضیه میلر با استفاده از تقویتکننده، ولتاژ ورودی ، به عنوان و ولتاژ خروجی ، به عنوان در نظر گرفته میشوند. در بسیاری از موارد، منبع ولتاژ ورودی دارای امپدانس ورودی است و یا یک امپدانس ورودی اضافی به آن متصل شده است که در ترکیب با ، موجب ایجاد یک فیدبک میشوند. بسته به نوع تقویتکننده (غیر معکوسکننده، معکوسکننده و تفاضلی)، فیدبک میتواند مثبت، منفی، و یا ترکیبی باشد.
آرایش تقویتکننده میلر دو جنبه مهم دارد:
- تقویتکننده ممکن است به صورت یک منبع ولتاژ اضافی در نظر گرفته شود، که امپدانس واقعی را به امپدانس مجازی تبدیل میکند (تقویتکننده امپدانس المان اصلی را اصلاح میکند).
- امپدانس مجازی میتواند به صورت یک المان در نظر گرفته شود، که به صورت موازی با ورودی تقویتکننده متصل میشود (امپدانس مجازی باعث اصلاح امپدانس ورودی تقویتکننده میشود).
کاربردهای قضیه میلر
افزودن یک امپدانس که پورت ورودی تقویتکننده را به خروجی آن متصل میکند، باعث افزایش پیچیدگی در فرایند آنالیز میشود. قضیه میلر به کاهش پیچیدگی در بعضی مدارات مخصوصا مدارات دارای فیدبک، کمک میکند و آنها را به مدارات معادل آسانتری برای تجزیه و تحلیل تبدیل میکند. اما قضیه میلر تنها ابزاری مناسب برای به دست آوردن مدار معادل نیست، بلکه ابزاری بسیار مفید در طراحی و درک مدارها بر اساس امپدانس اصلاح شده از طریق افزودن منبع ولتاژ است.
بر حسب پلاریته ولتاژ خروجی در مقایسه با ولتاژ ورودی و نسبت بین دامنه آنها، شش طبقهبندی وجود دارد که در جدول بالا به اختصار به آنها اشاره شد. در بعضی از این موارد، پدیده میلر به صورت اثرات ناخواسته مطلوب (Bootstrapping) یا غیرمطلوب (اثر میلر) ظاهر میشود.
کاربردهای مبتنی بر تفاضل از
در این کاربردها، ولتاژ خروجی با یک پلاریته که در جهت مخالف با ولتاژ ورودی است، در طول حلقه به گردش در میآید (اما پلاریته با توجه به زمین، یکسان است). در نتیجه، ولتاژ موثر و جریان در طول امپدانس، کاهش یافته و امپدانس ورودی افزایش مییابد.
امپدانس افزایش یافته
این حالت توسط یک تقویتکننده غیر معکوسکننده با بهره پیادهسازی میشود. دامنه ولتاژ خروجی کمتر از ولتاژ ورودی است و تا حدی آن را خنثی میکند. این حالت شامل تعقیبکنندههای ولتاژ غیرایدهآل (تعقیبکنندههای امیتر، سورس و کاتد) و تقویتکنندههای با فیدبک منفی سری است که امپدانس ورودی آنها نسبتا افزایش یافته است.
امپدانس بینهایت
امپدانس بینهایت از یک تقویتکننده غیر معکوسکننده استفاده میکند که در آن است. ولتاژ خروجی برابر با ولتاژ ورودی است و به صورت کامل آن را خنثی میکند. به عنوان نمونههایی از کاربردهای این حالت، میتوان به تعقیبکننده ولتاژ با تقویتکنندههای عملیاتی (بافر ولتاژ)، اندازهگیرهای نقطه خنثی (تعادل) پتانسیومتری (potentiometric null-balance meters) و تقویتکنندههای با فیدبک منفی سری اشاره کرد که در آنها امپدانس ورودی مدار فوقالعاده افزایش یافته است. به این تکنیک بوت استرپینگ (Bootstrapping) نیز گفته میشود و عمدتا در مدارات بایاس و مدارات محافظ ورودی به کار میرود. نمایی از مدار در امپدانس بینهایت در شکل زیر نشان داده شده است.
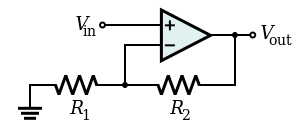
امپدانس منفی همراه با جریان معکوس
این حالت توسط تقویتکننده غیر معکوس کننده با پیادهسازی میشود. در این شرایط چون ولتاژ ورودی از ولتاژ خروجی بالاتر است، جریان جهت خود را تغییر میدهد. اگر منبع جریان ورودی، دارای امپدانس داخلی باشد، یا به یک المان امپدانسی دیگر متصل باشد، منجر به یک فیدبک مثبت میشود. یک کاربرد معمول، مبدل امپدانس منفی (Negative Impedance Converter) همراه با معکوس جریان است که هم از فیدبک مثبت و هم فیدبک منفی استفاده میکند. فیدبک منفی برای تحقق یک تقویتکننده غیر معکوسکننده و فیدبک مثبت برای اصلاح امپدانس مورد استفاده قرار میگیرند.
کاربردهای مبتنی بر جمع و
در این کاربرد، ولتاژ خروجی با پلاریته یکسان با منبع ولتاژ وارد مدار میشود اما در مقایسه با زمین دارای پلاریته مخالف است. در نتیجه، ولتاژ موثر و جریان در امپدانس افزایش مییابند و امپدانس ورودی کاهش مییابد.
امپدانس کاهش یافته
امپدانسِ کاهش یافته توسط یک تقویتکننده معکوسکننده پیادهسازی میشود که معمولا دارای بهره متوسط در بازه است و ممکن است به صورت اثر میلر نامطلوب در طبقه تقویتکننده امیتر مشترک، منبع مشترک و کاتد مشترک دیده شود که در آن ظرفیت خازنی موثر ورودی افزایش مییابد. جبرانساز فرکانسی برای تقویتکنندههای عملیاتی همهمنظوره و انتگرالگیرهای میلر ترانزیستوری مثالهایی از استفاده مفید از اثر میلر هستند.
امپدانس صفر شده
این مد از یک تقویتکننده عملیاتی معکوسکننده (اپ امپ) با بهره فوقالعاده بزرگ () استفاده میکند. ولتاژ خروجی همیشه برابر با افت ولتاژ در طول امپدانس است و کاملا آن را خنثی میکند. مدار همانند یک اتصال کوتاه عمل میکند و به عنوان یک زمین مجازی در ورودی ظاهر میشود. بنابراین نباید توسط یک منبع ولتاژ ثابت تغذیه شود. به این منظور، بعضی مدارات توسط یک منبع جریان ثابت یا منبع ولتاژ حقیقی با امپدانس داخلی تغذیه میشوند؛ مانند مبدلهای جریان به ولتاژ (تقویتکنندههای انتقال امپدانس)، انتگرالگیرهای خازنی، مبدلهای مقاومت به ولتاژ (یک سنسور مقاومتی که در محل امپدانس Z متصل شده باشد). شکل زیر نمایی از مدار اپ امپ تقویتکننده معکوسکننده برای پیادهسازی این حالت را نشان میدهد.
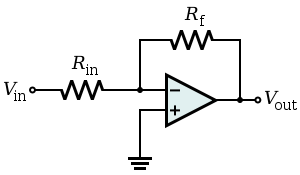
بقیه موارد دارای امپدانس اضافی هستند که به صورت سری به ورودی متصل شده است؛ مانند مبدلهای ولتاژ به جریان (تقویتکنندههای ترارسانایی)، تقویتکننده معکوسکننده، تقویتکننده جمعکننده، انتگرالگیر سلفی، تفریقکننده خازنی و انتگرالگیر خازنی-مقاومتی. انتگرالگیر معکوسکننده در این لیست مثالی از کاربرد مفید و مطلوب اثر میلر است.
در تمام این مدارات معکوسکننده اپ امپی با فیدبک منفی موازی، جریان ورودی به بیشینه خود افزایش مییابد. جریان فقط توسط ولتاژ ورودی و امپدانس ورودی بر اساس قانون اهم تعیین میشود و به امپدانس Z بستگی ندارد.
امپدانس منفی با جریان معکوس
این حالت توسط اعمال همزمان فیدبک منفی و مثبت به یک تقویتکننده عملیاتی با ورودی تفاضلی پیادهسازی میشود. منبع ولتاژ ورودی باید دارای امپدانس داخلی باشد و یا از طریق یک المان امپدانسی دیگر به ورودی متصل شود. تحت این شرایط، زمانی که ولتاژ خروجی از افت ولتاژ در طول امپدانس فراتر رود ()، ولتاژ ورودی در مدار پلاریته خود را تغییر میدهد.
یک کاربرد متداول این حالت، مبدلهای امپدانس منفی با ولتاژ معکوس است. جالب است که ولتاژ ورودی مدار با وجود اینکه به ورودی معکوسکننده اپ امپ اعمال شده است، اما دارای پلاریته یکسان با ولتاژ خروجی است. زیرا منبع ورودی پلاریته مخالف با ولتاژهای ورودی و خروجی مدار دارد.
تعمیم قضیه میلر
اصل اثر میلر توسط امپدانس خازنی متصل بین دو گره قابل پیادهسازی است. تئوری میلر، اثر میلر را به صورت اعمال اختیاری امپدانس Z بین گرهها تعمیم میدهد. همچنین یک ضریب ثابت K را فرض میکند. به جز این دو تغییر، تمام موارد ذکر شده در بالا صحیح است. اما حتی زمانی که این ملزومات نقض شوند، مشخصههای اصلاحشده تئوری میلر وجود دارند و این آرایش میتواند توسط تغییر امپدانس و ضریب تعمیم داده شوند.
المان غیرخطی
علاوه بر امپدانس، آرایش میلر می تواند منحنی مشخصه جریان-ولتاژ یک المان اختیاری را نیز اصلاح کند. مدار یک مبدل لگاریتمی دیودی مثالی از یک مقاومت غیرخطی است که در آن منحنی مشخصه نمایی جریان-ولتاژ بایاس مستقیم دیود به یک خط عمودی مستقیم دارای همپوشانی با محور Y تبدیل شده است.
ضریب غیرثابت
اگر ضریب K تغییر کند، المانهای ناشناختهای به دست میآیند. یک مدار ژیراتور، مثالی از چنین المان مجازی است که در آن مقاومت به نحوی اصلاح شده است که بتواند عکس مقاومت، خازن یا سلف را تقلید کند.
دوگان قضیه میلر (برای جریان)
دوگان قضیه میلر مربوط به حالتی است که دو منبع جریان مختلف، یک امپدانس زمین شده را تغذیه میکنند و بر اساس قانون جریان کیرشهف بنا شده است. این قضیه بیان میکند که اگر در مدار شاخهای با امپدانس Z متصل به یک گره وجود داشته باشد، که از طریق آن دو جریان و به زمین ختم شوند، میتوان این شاخه را با دو شاخه جایگزین کرد که جریانهای مذکور را از طریق امپدانسهای و به زمین هدایت میکنند و در آن است. دوگان قضیه میلر ممکن است با جایگزینی شبکه دو قطبی با معادل آن و سپس اعمال قضیه جذب منبع اثبات شود.
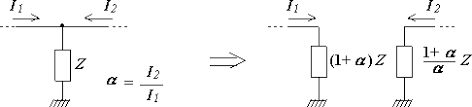
شرح قضیه
قضیه دوگان میلر در حقیقت بیان میکند که اتصال منبع جریان دوم، جریان نسبی را موازی با منبع ورودی اصلی ایجاد میکند و المان امپدانسی جریان عبوری، ولتاژ و به صورت متناظر امپدانس مدار دیده شده از طرفین منبع ورودی را تغییر میدهد. بسته به جهت، مانند یک منبع جریان اضافی عمل میکند که به منبع جریان اصلی برای ساخت ولتاژ در طول امپدانس کمک میکند و یا با آن مخالفت میکند. ترکیب منبع جریان اصلی و منبع جریان دوم میتواند به عنوان یک عنصر مجازی جدید با امپدانس دینامیکی اصلاحشده در نظر گرفته شود.
پیادهسازی
دوگان قضیه میلر، معمولا با آرایشی متشکل از دو منبع ولتاژ پیادهسازی میشود، که امپدانس Z را از طریق امپدانسهای متغیر تغذیه میکنند. ترکیب منابع ولتاژ و امپدانسهای متناظر، دو منبع جریان اصلی و کمکی را تشکیل میدهند. همانند قضیه میلر که در بالا توضیح داده شد، ولتاژ دوم همیشه توسط یک تقویتکننده ولتاژ ایجاد میشود. بسته به نوع تقویتکننده (معکوسکننده، غیر معکوسکننده و تفاضلی) و بهره آن، امپدانس ورودی مدار ممکن است به صورت مجازی افزایش یابد، به بینهایت برود، کاهش یابد و یا صفر یا منفی شود.
کاربردها
دوگان قضیه میلر نیز علاوه بر سادهتر کردن آنالیز مدارات، با افزودن جریان اضافی در طراحی راحتتر و درک بهتر مدارات مبتنی بر اصلاح امپدانس کمک میکنند. کاربردهای متداول شامل برخی مدارات با امپدانس منفی به عنوان لغوکننده بار (Load Canceller)، خنثیکننده ظرفیت خازنی و منابع جریان Howland هستند.
اگر مطالب بیان شده برای شما مفید بوده و میخواهید درباره موضوعات مرتبط با آن بیشتر بدانید، پیشنهاد میکنیم به آموزشهای زیر مراجعه کنید:
- مجموعه آموزشهای مهندسی برق
- آموزش الکترونیک ۳
- مجموعه آموزشهای نرمافزارهای مهندسی برق و الکترونیک
- آموزش مبانی الکترونیک – مفاهیم تئوریک به همراه شبیه سازی عملی و کاربردی
- امپدانس ورودی (Input Impedance) تقویت کننده — مفاهیم کلیدی
- تقویت کننده ها (Amplifiers) — به زبان ساده
- تقویت کننده های الکترونیکی — مجموعه مقالات جامع وبلاگ فرادرس
^^












