فشار هیدرواستاتیک و محاسبه آن — به زبان ساده

در راستای تشریح مفاهیم مرتبط با مکانیک سیالات، در این مطلب میخواهیم در مورد محاسبه نیروی ناشی از فشار هیدرواستاتیک صحبت کنیم. البته قبل از مطالعه این مطلب، پیشنهاد میشود مطالب استاتیک سیالات، مفاهیم فشار و سینماتیک سیالات را مطالعه فرمایید.
فشار هیدرواستاتیک و نیرو
در ابتدا فرض کنید صفحهای به صورت عمودی در آب قرار داده شده و هدف محاسبه فشار هیدرواستاتیک وارد شده به صفحه از جانب آب است. توجه داشته باشید که در حالت کلی این صفحه میتواند دارای هر شکل دلخواهی باشد. از کاربردهای تحلیل چنین مسئلهای، محاسبه نیروی وارد شده به دریچههای قرار گرفته جلوی سد است.
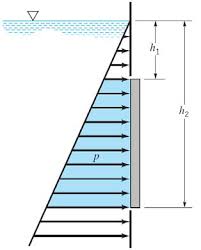
دو رابطه کلی به منظور محاسبه فشار وجود دارد. در ابتدا باید بگوییم که فشار در فاصله $$d$$، زیر سطح آزاد برابر است با:
$$ \large P = \rho g d $$
در رابطه فوق، $$\rho$$ چگالی سیال و $$g$$ شتاب گرانشی را نشان میدهند. فرض بر این است که سیال مورد استفاده، آب است. نهایتا چگالی و شتاب گرانشی را برای این مسئله به صورت زیر در نظر میگیریم.
$$\rho = 1000 {\mbox{ kg/} } { { \mbox{m}}^{\mbox{3}}} \hspace {0.25in} , \ \ \ \ \ g = 9.81 {\mbox{ m/} } { {\mbox{ s } } ^ {\mbox{2}}}$$
با فرض اینکه فشار هیدرواستاتیک و مساحت سطح صفحه به ترتیب برابر با $$P$$ و $$A$$ باشند، نیروی هیدرواستاتیک وارد به صفحه برابر است با:
$$ \large F = P A $$
توجه داشته باشید که به منظور محاسبه مجموع نیروی وارد به یک صفحه نمیتوان به طور مستقیم از رابطه فوق استفاده کرد. با توجه به تغییرات فشار در راستای عمودی باید با استفاده از انتگرال، نیروی کل وارد به صفحه را محاسبه کرد. در ادامه و در قالب مثال نحوه در نظر گرفتن دیفرانسیل مناسب به منظور محاسبه نیروی وارد به صفحه را توضیح خواهیم داد.
مثال ۱
مطابق با شکل زیر صفحهای مثلثی شکل در مخزنی از آب به ارتفاع $$4$$ متر قرار گرفته است. نیروی ناشی از فشار هیدرواستاتیک که به سطح وارد میشود، چقدر است؟
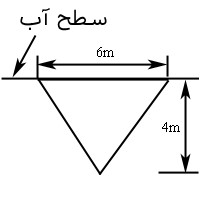
به منظور بدست آوردن نیروی هیدرواستاتیکی در اولین قدم باید محورهای دستگاه مختصات را مشخص کرد. از این رو در ادامه، شکل فوق به همراه محور $$x$$ نشان داده شده است.
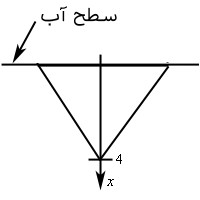
همانطور که در شکل نشان داده شده، جهت محور $$x$$ به سمت پایین در نظر گرفته شده و نقطه $$x=0$$ نشان دهنده سطح آب است. بنابراین نوک مثلث در مختصات $$x=4$$ قرار میگیرد. در مرحله بعد سطح را به $$n$$ قسمت با عرض $$\Delta x$$ تقسیمبندی میکنیم. همچنین فرض کنید که مختصات مرکز هریک از این نوارها را با $$ x ^ { * } _ i $$ نشان دهیم. در شکل زیر تقسیمبندی و نمادگذاری مذکور نشان داده شدهاند.
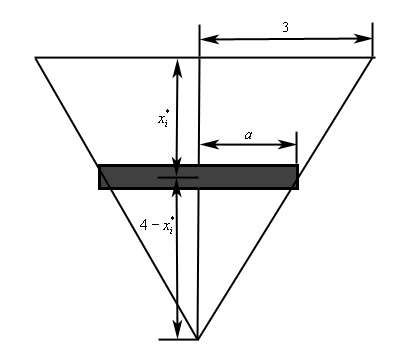
با توجه به شکل فوق، میتوان از قضیه تالس به منظور یافتن مقدار مجهول $$a$$ استفاده کرد. با استفاده از این قضیه داریم:
$$ \large \frac { 3 } { 4 } = \frac { a } {{ 4 - x _ i ^ * } } \ \ \Rightarrow \ \ a = 3 - \frac { 3 } { 4 } x _ i ^ * $$
رابطه کلی فشار با افزایش عمق را میتوان با استفاده از قانون هیدرواستاتیک و به صورت زیر بدست آورد.
$$\large { P _ i } = \rho g d = 1000 \left ( { 9.81 } \right) x _i ^ * = 9810 x _ i ^ * $$
بنابراین فشار روی هر نوار برابر است با:
$$ \large \begin {align*} { F _ i } & = { P _ i } \, A \\ & = { P_ i } \left ( { 2 a \Delta x } \right) = 9810 x _ i ^ * \left( 2 \right ) \left( {3 - \frac { 3 }{ 4 } x _ i ^ * } \right ) \Delta x \\ & = 19620 x _ i ^ * \left( {3 - \frac{3}{ 4 } x _ i ^ * } \right) \, \Delta x \end {align*} $$
بنابراین مقدار نیرو برابر با حاصل جمع نیرو روی هریک از نوارها است. در نتیجه میتوان گفت:
$$\large F \approx \sum \limits _ { i = 1 } ^ n { 19620x_i ^ * \left ( { 3 - \frac { 3 }{ 4 } x _ i ^ *} \right)} \, \Delta x$$
این مقدار زمانی دقیق خواهد بود که طولهای $$\Delta x$$ کوچک در نظر گرفته شوند. عدد فوق معادل با انتگرال زیر است.
$$\large F = \int _ { { \, 0 } }^ { { \, 4 } } {{ 19620 \left ( { 3 x - \frac { 3 } {4 } { x ^2 } } \right ) \, d x } } $$
بنابراین نیروی هیدرواستاتیک برابر است با:
$$\large \begin {align*} F &= \int_{{\,0}}^{{\,4}}{{19620\left( {3x - \frac { 3 } {4 } { x ^2 } } \right)\, d x } } \\ & = \left. {19620 \left ( { \frac { 3 }{ 2 } { x ^ 2 } - \frac { 1 } { 4 } { x ^3 } } \right)} \right| _ 0 ^ 4 \\ & = 156960 \, N \end{align*} $$
مثال ۲
نیروی هیدرواستاتیک وارد به دریچهای دیسکی شکل، به شعاع $$2$$ متر را بیابید. فرض کنید این دریچه در مخزنی به عمق $$6$$ متر قرار داده شده است.
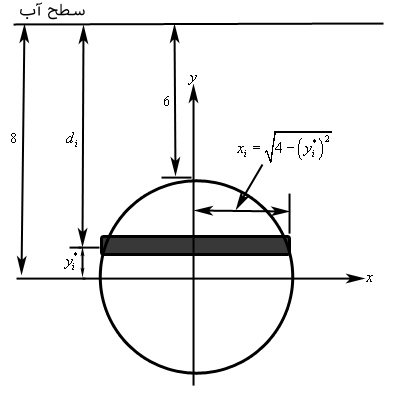
همانطور که در شکل نیز نشان داده شده، دیفرانسیلهای مستطیلی شکل در ارتفاع $$d_i$$ نسبت به سطح آزاد قرار گرفتهاند. این فاصله را میتوان بر حسب $$y ^ * _ i $$ به صورت زیر بیان کرد:
$$ \large { d _i } = 8 - y _ i ^ * $$
بنابراین فشار روی سطوح برابرند با:
$$\large { P _i } = \rho g { d _ i } = 9810 \left ( { 8 - y _ i ^ * } \right ) $$
از طرفی مساحت هریک از مستطیلها نیز مطابق با رابطه زیر محاسبه میشود.
$$\large { A _ i } = 2 \sqrt { 4 - { { \left ( { y _ i ^ * } \right ) }^2 } } \,\,\Delta y $$
با استفاده از دو رابطه فوق، فشار روی هر نوار یا همان مستطیل به صورت زیر بدست خواهد آمد.
$$\large \begin{align*} F & = \mathop { \lim }\limits_{n \to \infty } \sum \limits _ { i = 1 } ^ n {19620\left( {8 - y_i^*} \right)\sqrt {4 - {{\left( {y_i^*} \right)}^2}} \,\,\Delta y} \\ & = 19620 \int _ { { \, - 2} } ^ { { \,2}} { {\left( {8 - y} \right ) \sqrt { 4 - { y ^ 2 } } \, d y }} \end{align*}$$
برای بدست آوردن کل نیرو، باید جمع نیروها را روی تمامی نوارها محاسبه کنیم. بنابراین کل نیرو برابر است با:
$$ \large F = 19620\int_{{\, - 2} } ^ { { \,2 } }{ {8\sqrt {4 - { y ^2 } } \, d y } } - 19620\int_{{\, - 2 } } ^ { { \, 2 } } { { y \sqrt { 4 - { y ^2 }} \, d y } }$$
به منظور حل انتگرال اول باید از تغییر متغیر مثلثاتیِ $$ y = 2 \sin \theta $$ استفاده کنیم. همچنین انتگرال دوم را میتوان با استفاده از تغییر متغیر $$ v = 4 - { y ^ 2 } $$ حل کرد. پس از حل انتگرال فوق با استفاده از این تغییر متغیرها، نیروی $$F$$ به صورت زیر بدست خواهد آمد.
$$ \large \begin{align*}F & = 627840\int_{{\, - {\pi }/{2}\;}}^{{\,{\pi }/{2}\;}}{{{{\cos } ^2 } \theta \,d\theta }} + 9810\int_{{\,0} }^ { { \,0}}{{\sqrt v \,dv}}\\ & = 313920\int_{{\, - { \pi } /{2}\;} } ^ { { \,{\pi }/{2}\;}}{{1 + \cos \left( {2\theta } \right)\,d\theta }} + 0\\ & = 313920\left. {\left( {\theta + \frac{1}{2}\sin \left( {2\theta } \right)} \right)} \right|_{ - \frac { \pi } { 2 } } ^ { \frac { \pi } { 2 } } \\ & = 313920\pi \end{align*}$$
مثال ۳
نیروی ناشی از فشار هیدرواستاتیک را روی سطح زیر بدست آورید.
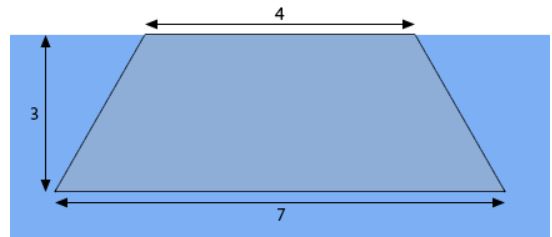
همانطور که در بالا نیز بیان شد در اولین قدم باید محور مختصات را به درستی تعیین کرد. در شکل زیر این محور نشان داده شده است.

با توجه به شکل فوق، نقطه $$x=0$$ نشان دهنده سطح آزاد مخزن است. دیفرانسیلها (یا همان مستطیلها) را نیز در شکل زیر میبینید.
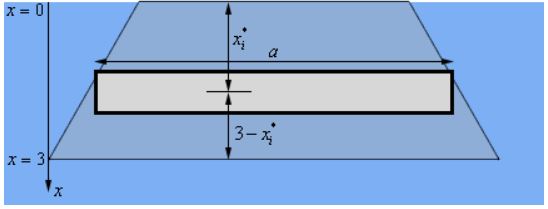
همانطور که در شکل نیز نشان داده شده، $$x_i^*$$ فاصله نوارها را از سطح آزاد نشان میدهد. قضیه تالس را میتوان مطابق با شکل زیر بیان کرده و با استفاده از آن مقدار $$b$$ را بدست آورد.
$$\large \frac { b } { { 3 - x _ i ^* } } = \frac { { 1.5 } } { 3 } \hspace {0.25in} \hspace{0.25in} \Rightarrow \ \ b = \frac { 1 } {2 } \left ( { 3 - x _ i ^ * } \right)$$
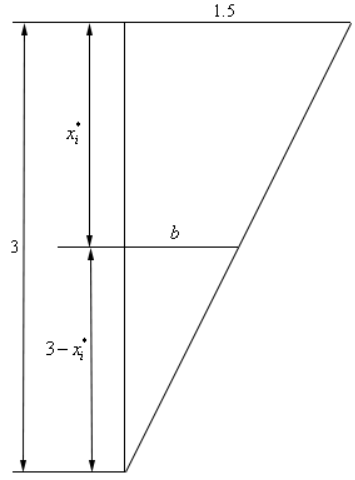
با بدست آمدن $$b$$، مقدار $$a$$ یا همان طول هریک از مستطیلها نیز به صورت زیر بدست میآید.
$$ \large a = 7 - 2 b = 7 - 2 \left ( { \frac { 1 } { 2 } } \right ) \left ( { 3 - x _ i ^ * } \right ) = 4 + x _ i ^ * $$
از طرفی اندازه فشار هیدرواستاتیک روی هریک از نوارها برابر است با:
$$ \large { P _ i } = \rho g { d _ i } = \left ( { 1000 } \right ) \left ( {9.81} \right) x _ i ^ * = 9810 x_ i ^ * $$
در نتیجه نیروی هیدرواستاتیک نیز روی هریک از نوارها مطابق با رابطه زیر بدست خواهد آمد.
$$ \large { F _ i } = { P _ i } { A_ i } = \left ( { 9810 x _ i ^ * } \right ) \left[ {\left ( { 4 + x _ i ^ * } \right ) \left ( { \Delta \, x } \right ) } \right] = 9810 \left[ { 4 x _ i ^ * + { { \left ( { x _ i ^ * } \right ) } ^ 2 } } \right] \Delta \, x $$
بدیهی است که نیروی وارد شده به کل سطح، برابر با حاصل جمع نیروی وارد به هریک از بخشها خواهد بود.
$$ \large { F \approx \sum \limits _ { i = 1 } ^ n { 9810 \left[ { 4 x _ i ^ * + { { \left ( { x _ i ^ * } \right ) } ^ 2 } } \right] \Delta \, x } } $$
به منظور بدست آوردن مقدار دقیق، باید حد نیروی $$F$$ را در بینهایت محاسبه کرد. در این صورت این نیرو را میتوان به صورت حد زیر بیان کرد:
$$ \large F = \mathop { \lim }\limits_{n \to \infty } \sum\limits _ { i = 1 } ^ n { 9810 \left[ { 4 x _ i ^ * + { { \left ( { x _ i ^ * } \right ) } ^ 2 } } \right] \Delta \, x } $$
نهایتا با استفاده از مفهوم انتگرال، مقدار نیرو برابر میشود با:
$$\large \begin {align*} F = \int _ { 0} ^{ 3 } { { 9810\left( {4 x + { x^ 2 } } \right ) d x } } & = \left. {9810\left ( { 2{ x ^2 } + \frac { 1 } {3 } {x ^ 3 } } \right ) } \right | _ 0 ^ 3 \\ & = { { 264,870N } } \end {align*} $$
همانطور که در مثالهای فوق نیز نشان داده شد، برای محاسبه مقدار نیروی ناشی از فشار هیدرواستاتیک وارد به سطح در ابتدا باید دیفرانسیلهای سطحی را در نظر گرفت؛ پس از آن فشار هیدرواستاتیک را روی هریک از سطوح محاسبه کرده و نهایتا با استفاده از انتگرالگیری مقدار کل نیرو را محاسبه میکنیم.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:











عالی مرسی از وقتتون