فرمول مساحت متوازی الاضلاع چیست؟ – تمامی فرمول ها + حل تمرین و مثال
فرمول مساحت متوازی الاضلاع «قاعده ضربدر ارتفاع» با عبارت جبری S=bh است. متوازیالاضلاع، یک چهارضلعی با ضلعهای موازی است. شکلهای هندسی شناخته شده نظیر مربع و مستطیل، از انواع خاص متوازیالاضلاع به شمار میآیند. در این آموزش از مجله فرادرس، انواع فرمول مساحت متوازی الاضلاع (با قاعده، ارتفاع، قطر و زاویه) را به همراه حل چند مثال معرفی کنیم.


مساحت متوازی الاضلاع چیست؟
در مطلب «مساحت متوازی الاضلاع چیست؟ — فیلم آموزش رایگان + حل تمرین و مثال» از مجله فرادرس، مساحت متوازیالاضلاع را تعریف کردیم.
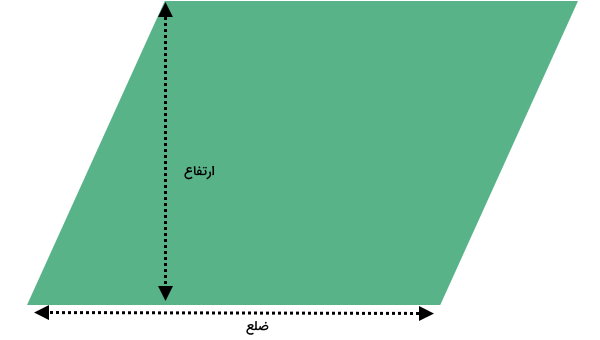
مساحت متوازیالاضلاع، اندازه سطح درون ضلعهای این شکل هندسی است. ناحیه زرد رنگ در تصویر زیر، مساحت یک متوازیالاضلاع را نمایش میدهد.

مساحت متوازی الاضلاع چگونه محاسبه میشود؟
مساحت متوازیالاضلاع با ضرب اندازه یکی از ضلعها در ارتفاع نظیر آن ضلع محاسبه میشود.
به عنوان مثال، اگر اندازه یکی از ضلعهای متوازیالاضلاع برابر 7 و ارتفاع نظیر ضلع برابر 3 باشد، مساحت آن برابر است با:
۲۱ = ۳ × ۷ = مساحت متوازیالاضلاع
فرمول مساحت متوازی الاضلاع چیست؟
فرمول مساحت متوازیالاضلاع به صورت زیر نوشته میشود:
ارتفاع × قاعده = مساحت متوازیالاضلاع
منظور از قاعده متوازیالاضلاع در فرمول بالا، ضلعی است که ارتفاع آن را داریم. با این وجود، معمولا ضلع پایینی متوازیالاضلاع به عنوان قاعده آن معرفی میشود.
مثال 1: محاسبه مساحت متوازی الاضلاع با قاعده و ارتفاع
تصویر زیر، یک متوازیالاضلاع و اندازه دو ضلع مجاور آن را نمایش میدهد. اگر ارتفاع نظیر طول متوازیالاضلاع، برابر ۳ باشد، مساحت آن چقدر خواهد بود؟
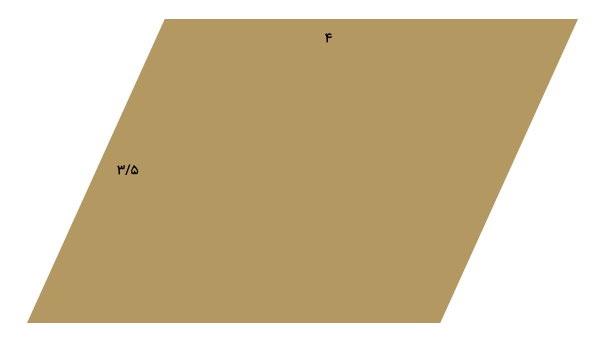
متوازیالاضلاع بالا، دارای دو ضلع به اندازههای 4 و 3/5 است. ضلع بزرگ این متوازیالاضلاع، به عنوان طول و ضلع کوچک آن، به عنوان عرض در نظر گرفته میشود. به منظور تعیین مساحت، فرمول آن را مینویسیم:
ارتفاع × قاعده = مساحت متوازیالاضلاع
مطابق با صورت سوال، ارتفاع نظیر طول متوازیالاضلاع را داریم. این اندازه برابر ۳ است. بنابراین، به جای قاعده در فرمول بالا، باید اندازه طول متوازیالاضلاع، یعنی 4 را قرار دهیم:
3 × 4 = مساحت متوازیالاضلاع
۱۲ = مساحت متوازیالاضلاع
در نتیجه، مساحت متوازیالاضلاع برابر 12 واحد سطح است. واحد سطح، معمولا به صورت طول مربع (سانتیمتر مربع، متر مربع، اینچ مربع و غیره) بیان میشود.
فرمول مساحت متوازی الاضلاع به صورت جبری
متوازیالاضلاع زیر را در نظر بگیرید. در این متوازیالاضلاع، اندازه قاعده و ارتفاع نظیر را با حروف انگلیسی h و b مشخص کردهایم.
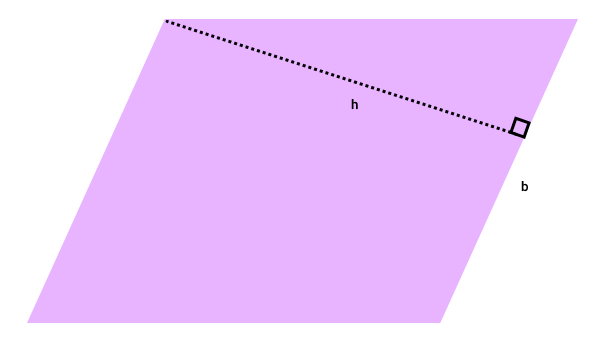
فرمول کلامی مساحت متوازیالاضلاع به صورت زیر نوشته میشود:
ارتفاع × قاعده = مساحت متوازیالاضلاع
به جای قاعده، حرف b و به جای ارتفاع، حرف h را قرار میدهیم:
b × h = مساحت متوازیالاضلاع
در اغلب فرمولهای ریاضی، از حرف S یا A برای نمایش مساحت استفاده میشود. بنابراین، میتوانیم عبارت جبری فرمول مساحت متوازیالاضلاع را به صورت زیر بنویسیم:
به فرم نوشتاری بالا، عبارت جبری میگویند. عبارتهای جبری، به منظور نمایش رابطه بین اندازههای مختلف توسط ثابتهای عددی، متغیرها (حروف انگلیسی یا یونانی) و عملهای ریاضی (جمع، ضرب و غیره) مورد استفاده قرار میگیرند.
مثال 2: محاسبه مساحت متوازی الاضلاع به صورت جبری
مساحت متوازیالاضلاعی زیر را حساب کنید.
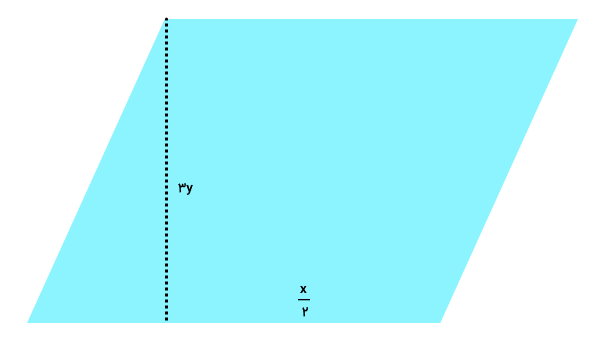
برای حل این مثال، فرمول مساحت متوازی الاضلاع به صورت جبری را مینویسیم:
- S: مساحت متوازیالاضلاع
- b: قاعده متوازیالاضلاع
- h: ارتفاع نظیر قاعده
اکنون، اندازههای داده شده را درون فرمول بالا قرار میدهیم:
مساحت متوازیالاضلاع به صورت جبری به دست آمد. در صورت مشخص بودن اندازه x و y، میتوانیم مقادیر عددی آنها را درون رابطه بالا قرار داده و مقدار مساحت را تعیین کنیم. در صورت تمایل به مشاهده مثالهای متنوع بیشتر در رابطه با مساحت متوازیالاضلاع، مطالعه مطلب «نمونه سوال مساحت متوازیالاضلاع با جواب — حل تمرینهای متنوع» از مجله فرادرس را به شما پیشنهاد میکنیم.
انواع فرمول های مساحت متوازی الاضلاع
مساحت متوازی الاضلاع، فرمولهای متنوعی دارد. در صورت مشخص بودن اندازه ضلعها، قطرها و زاویهها، امکان محاسبه مساحت متوازی الاضلاع بدون ارتفاع فراهم میشود. جدول زیر، انواع فرمول مساحت متوازی الاضلاع و اندازههای مورد نیاز برای استفاده از آنها را نمایش میدهد.
| عنوان فرمول | اندازههای مورد نیاز | عبارت جبری |
| مساحت با قاعده و ارتفاع | b: قاعده متوازیالاضلاع
h: ارتفاع نظیر قاعده | |
| مساحت با دو ضلع | a: یکی از ضلعها
b: ضلع مجاور a x: زاویه بین a و b | |
| مساحت با قطر | d1: قطر اول
d2: قطر دوم y: زاویه بین دو قطر | |
| مساحت با ضرب خارجی ضلعها | a: بردار یکی از ضلعها
b: بردار ضلع مجاور a | |
| مساحت با ضرب خارجی قطرها | d1: بردار قطر اول
d2: بردار قطر دوم |
مثال 3: محاسبه مساحت متوازی الاضلاع با دو ضلع
اندازه دو ضلع مجاور متوازیالاضلاعی برابر 12 و 5 سانتیمتر است. با فرض زاویه 30 درجه بین این دو ضلع، مساحت متوازیالاضلاع را به دست بیاورید.
به منظور حل این مسئله از فرمول مساحت متوازیالاضلاع با دو ضلع استفاده میکنیم:
- S: مساحت متوازیالاضلاع
- a: اندازه یک ضلع برابر 12 سانتیمتر
- b: اندازه ضلع مجاور a برابر 5 سانتیمتر
- x: زاویه بین a و b برابر 30 درجه
اندازههای معلوم را درون فرمول بالا قرار میدهیم:
سینوس زاویه 30 درجه برابر یکدوم است:
در نتیجه، مساحت متوازیالاضلاع برابر ۳۰ سانتیمتر مربع است.
مثال 4: محاسبه مساحت متوازی الاضلاع با دو قطر
متوازیالاضلاعی به قطرهای 7 و 13 متر را در نظر بگیرید. اگر دو قطر، همدیگر را با زاویههای 120 درجه و 60 درجه قطع کنند، مساحت متوازیالاضلاع چقدر خواهد بود؟
فرمول مساحت متوازیالاضلاع با قطر به صورت زیر نوشته میشود:
- S: مساحت متوازیالاضلاع
- d1: قطر اول برابر 7 متر
- d2: قطر دوم برابر 13 متر
- y: زاویه بین دو قطر برابر 120 یا 60 درجه
دقت کنید که در صورت قرار دادن هر یک از زاویههای 60 یا 120 در فرمول بالا، نتیجه تغییر نمیکند. در اینجا، زاویه 60 درجه را درون فرمول قرار میدهیم:
سینوس زاویه 60 درجه تقریبا برابر 0/87 است:
در نتیجه، مساحت متوازیالاضلاع برابر ۳۹/۵۸ متر مربع است.
سوالات متداول فرمول مساحت متوازی الاضلاع
در این بخش، به برخی از سوالات متداول در رابطه با فرمول مساحت متوازیالاضلاع، به طور خلاصه پاسخ میدهیم.
محاسبه مساحت متوازی الاضلاع چگونه است؟
مساحت متوازیالاضلاع، حاصلضرب قاعده در ارتفاع نظیر آن است.
رابطه مساحت متوازیالاضلاع چگونه نوشته میشود؟
رابطه کلامی مساحت متوازیالاضلاع، به صورت «ارتفاع × قاعده» نوشته میشود.
فرمول مساحت متوازیالاضلاع با عبارت جبری چیست؟
عبارت جبری مساحت متوازیالاضلاع، S=bh است.
آیا میتوان مساحت متوازیالاضلاع را بدون ارتفاع به دست آورد؟
بله. در صورت داشتن اندازههای دیگری نظیر دو قطر و زاویه بین آنها، دو ضلع و زاویه بین آنها یا بردارهای معرف ضلعها یا قطرها، امکان محاسبه مساحت متوازیالاضلاع فراهم میشود.
آزمون مساحت متوازیالاضلاع
۱. فرمول استاندارد مساحت متوازیالاضلاع با نمادگذاری ریاضی چگونه بیان میشود؟
A = d₁ × d₂ برای دو قطر
P = a × b برای طول دو ضلع مجاور
M = ab + cd برای جمع چهار ضلع
S = b × h برای قاعده (b) و ارتفاع (h)
فرمول معتبر و پذیرفته شده برای محاسبه مساحت متوازیالاضلاع "S = b × h" است که در آن b نمایانگر طول قاعده (base) و h نماد ارتفاع (height) است.
۲. کدام ویژگی باعث میشود مربع و مستطیل جزو حالتهای خاص متوازیالاضلاع باشند؟
همه اضلاع آنها موازی با یکدیگرند.
همه زاویههای آنها قائمه است.
هر دو دارای اضلاع برابر هستند.
هر دو مانند متوازیالاضلاع اضلاع روبهرو موازی دارند.
ویژگی مشترک مهم بین مربع، مستطیل و متوازیالاضلاع این است که اضلاع روبهرو در هر سه شکل موازی با یکدیگر هستند. این داشتن اضلاع روبهرو موازی، تعریف اصلی متوازیالاضلاع است و مستطیل و مربع را در ردهی حالتهای خاص آن قرار میدهد. در حالی که داشتن زاویه قائمه یا اضلاع برابر، ویژگیهای اضافی مربع و مستطیل هستند، نه ویژگی لازم برای متوازیالاضلاع بودن.
۳. اگر طول دو ضلع مجاور و اندازه زاویه بین آنها در یک متوازیالاضلاع مشخص باشد، برای محاسبه مساحت باید از کدام فرمول استفاده کرد؟
فرمول قاعده تقسیم بر نیمساز زاویه
فرمول دو ضلع و سینوس زاویه بینشان (S = ab sin(x))
فرمول قاعده ضربدر ارتفاع (S = bh)
فرمول قطرها و سینوس زاویه بینشان (S = 1/2 d₁d₂ sin(y))
هنگامی که اندازه دو ضلع مجاور و زاویه بین آنها معلوم باشد، بهترین روش استفاده از فرمول «دو ضلع و سینوس زاویه بینشان» یعنی S = ab sin(x) است. این فرمول نیازی به دانستن ارتفاع یا طول قطرها ندارد. روش «قاعده ضربدر ارتفاع» فقط زمانی مناسب است که مقدار ارتفاع داده شده باشد.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- متوازی الاضلاع چیست ؟ — تعریف و مفاهیم به زبان ساده
- محیط متوازی الاضلاع چیست ؟ — به زبان ساده + حل تمرین و مثال
- فرمول محیط متوازی الاضلاع چیست ؟ — معرفی انواع فرمول ها + حل مثال
- مساحت متوازی الاضلاع چطور محاسبه می شود؟ – جامع + مثال، تمرین و فیلم رایگان
- محاسبه قطر متوازی الاضلاع — فرمول های محاسبه + حل تمرین و مثال
- محیط متوازی الاضلاع به صورت جبری — فرمول های ریاضی + حل مثال
- فرمول مساحت متوازی الاضلاع چیست ؟ — تمامی فرمول ها + حل تمرین و مثال(همین مطلب)
- مساحت متوازی الاضلاع به صورت جبری — انواع فرمول ها + حل مثال
- نمونه سوال مساحت متوازی الاضلاع با جواب — حل تمرین های متنوع
- مساحت متوازی الاضلاع با قطر چگونه بدست می آید ؟ + حل مثال
- مساحت متوازی الاضلاع با سینوس — به زبان ساده + حل مثال













خیییییییییییییلی خوب