فرادرسضرب اعداد مخلوط — به زبان ساده + حل تمرین و مثال
در آموزش‌های قبلی مجله فرادرس، با اعداد مخلوط آشنا شدیم. همچنین، با روش جمع اعداد مخلوط و تفریق آن‌ها را بیان کردیم. در این آموزش، می‌خواهیم با نحوه ضرب اعداد مخلوط آشنا شویم. پیش از آن، مروری کوتاه بر اعداد مخلوط را بیان می‌کنیم. در انتها نیز مثال‌هایی را بررسی خواهیم.
عدد مخلوط چیست؟
کلمه «مخلوط» در لغت به‌معنی «آمیخته‌شده» و «درهم‌شده» است. از این معنی درمی‌یابیم که وقتی یک چیز مخلوط داریم یعنی دو چیز در کنار هم قرار دارند و یک چیز را ساخته‌اند. به همین ترتیب، عدد مخلوط عددی است که از دو عدد ساخته شده است: یکی از این دو عدد صحیح است و دیگری کسر سره (کسری که قدر مطلق مخرجش از قدر مطلق صورتش بزرگ‌تر است).
عدد مخلوط از عبارت انگلیسی "Mixed Number" گرفته شده که البته، فرهنگستان زبان و ادب فارسی، برابرنهاد «عدد آمیخته» را برای آن پیشنهاد کرده است. بنابراین، اگر جایی عبارت عدد آمیخته آمده را دیدید، منظور آن همان عدد مخلوط است.
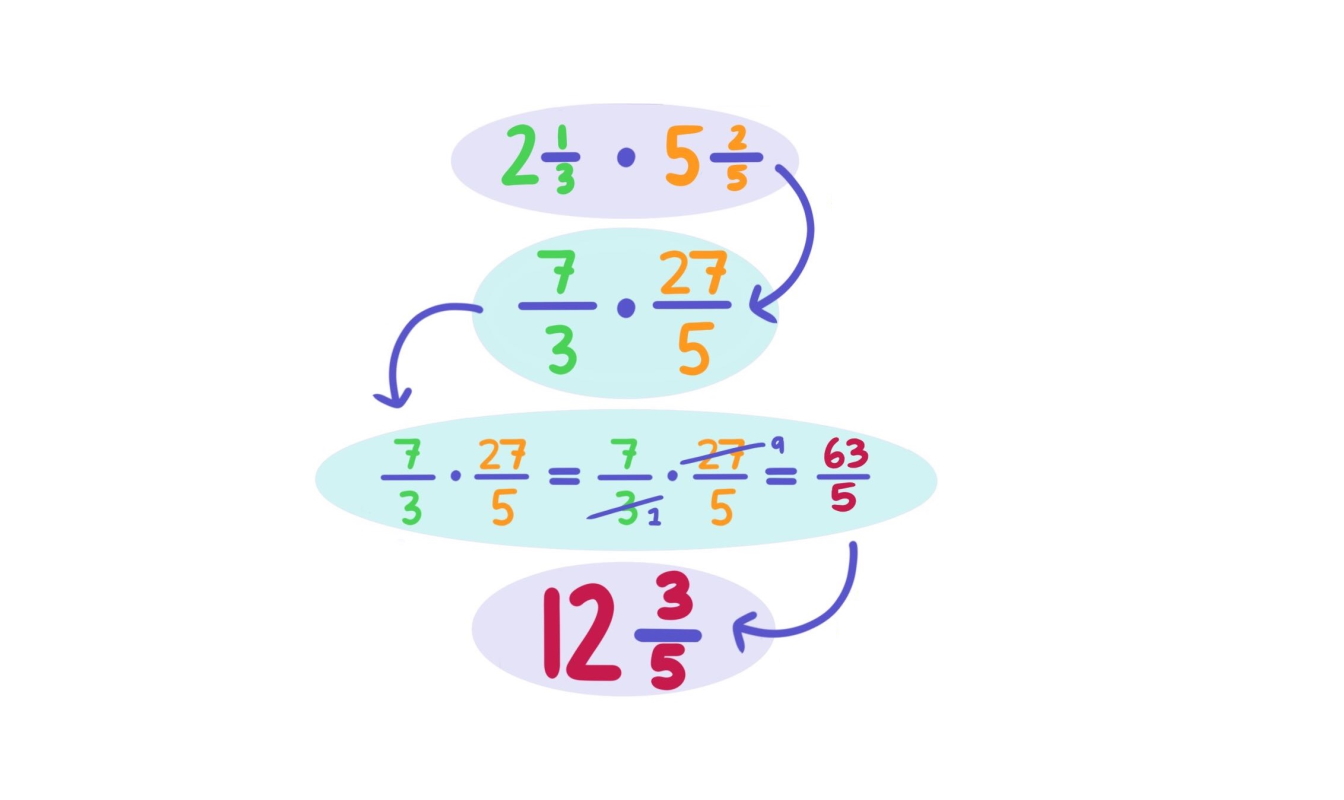
تصویر زیر یک کسر را نشان می‌دهد که بزرگ‌تر از ۱ کوچک‌تر از ۲ است. می‌بینیم که با یک عدد مخلوط مواجه هستیم، زیرا یک عدد صحیح و یک عدد کسری داریم. این یک نشان‌دهنده عدد صحیح و خرده‌ای همان عدد کسری است.
چند عدد مخلوط دیگر در زیر آورده شده‌اند:
$$ 3 \frac 12 , \; 2 \frac 35 , \; 5 \frac 35 , \; 4 \frac 15 $$
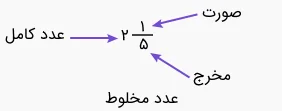
همان‌طور که در بالا گفتیم، یک عدد مخلوط دو بخش دارد: یک عدد صحیح یا کامل و یک عدد کسری. به عبارت دیگر، عدد مخلوط از سه عدد دیگر تشکل می‌شود: یکی عدد صحیح، یکی صورت کسر و یکی مخرج کسر.
شکل زیر سه بخش عدد مخلوط را نشان می‌دهد. این عدد را این‌گونه می‌خوانیم: دو و یک‌پنجم.
برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
تبدیل کسر به عدد مخلوط
کسر ناسره را می‌توان به عدد مخلوط تبدیل کرد. کسر ناسره به کسری میگویند که قدر مطلق صورتش از قدر مطلق مخرجش بزرگ‌تر است. از انجا که این کسر بزرگ‌تر از یک است می‌توان آن را به‌صورت یک عدد مخلوط نوشت. برای تبدیل کسر به عدد مخلوط می‌توان از روش‌های مختلفی استفاده کرد که در ادامه آن‌ها را معرفی می‌کنیم.
روش اول: تقسیم صورت بر مخرج
در این روش، باید گام‌های زیر را طی کنید:
- صورت را بر مخرج کسر تقسیم کنید.
- پس از انجام تقسیم، یک عدد به‌عنوان خارج قسمت خواهید داشت که همان عدد صحیح کسر مخلوط است.
- باقیمانده تقسیم صورت کسر عدد مخلوط است.
- مخرج کسر نیز همان مخرج عدد اصلی است.
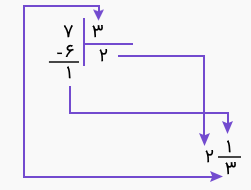
برای مثال، کسر $$ \frac 7 3 $$ را به یک عدد مخلوط تبدیل می‌کنیم:
- عدد $$7$$ را بر $$3 $$ تقسیم می‌کنیم.
- خارج قسمت را به‌عنوان عدد صحیح می‌نویسیم.
- باقیمانده را در صورت کسر و مقسوم‌علیه را در مخرج کسر می‌نویسیم.
مراحل بالا در شکل زیر نشان داده شده‌اند.
روش دوم: شکستن صورت کسر
در این روش، صورت کسر را می‌شکنیم که بخشی از آن به اندازه عدد مخرج کسر است. مثلاً عدد مخلوط $$ \frac {16}{5}$$ این‌گونه به عدد مخلوط تبدیل می‌شود:
$$ \frac {16}{5} = \frac {5+5+5+1}{5} = \frac 55 + \frac 55 +\frac 55 + \frac 15 =1+1+1+\frac 15=3\frac 15$$
برای آشنایی بیشتر با تبدیل کسر به عدد مخلوط، به آموزش «تبدیل کسر به عدد مخلوط — به زبان ساده + حل تمرین و مثال» مراجعه کنید.
تبدیل عدد مخلوط به کسر
تبدیل عدد مخلوط به کسر ساده است. برای این کار، ابتدا یک مخرج مشترک می‌گیریم، سپس عدد کامل را به‌صورت یک کسر می‌نویسیم که مخرج آن همان مخرج کسر مربوط به عدد مخلوط است. سپس آن را با کسر عدد مخلوط جمع می‌کنیم. برای مثال، عدد مخلوط $$3\frac 5 7 $$ را به کسر تبدیل می‌کنیم. ابتدا می‌توانیم عدد را این‌گونه:
$$ 3\frac 5 7 =3+\frac57$$
اکنون با در نظر گرفتن مخرج $$ 7$$، عدد $$3$$ را به یک کسر تبدیل می‌کنیم:
$$ 3 = \frac {3\times 7}{7} = \frac {21}{7}$$
بنابراین، عدد مخلوط به‌صورت زیر است:
$$ 3\frac 5 7 =3+\frac57= \frac {3\times 7}{7}+\frac 57 =\frac {21}{7}+\frac 57=\frac {21+5}{7}=\frac {26}{7}$$
جمع و تفریق اعداد مخلوط
جمع اعداد مخلوط به‌سادگی و با طی کردن مراحل ساده‌ای قابل انجام است. برای مثال، فرض کنید می‌خواهیم دو عدد $$5\frac 13 $$ و $$7 \frac 13$$ را با هم جمع کنیم.
برای این کار، ابتدا دو عدد مخلوط را به دو کسر تبدیل می‌کنیم که روش این کار را در بخش قبل گفتیم: $$5\frac 13 = \frac {16}{3}$$ و $$7\frac13=\frac{22}{3}$$.
در ادامه، دو عدد کسری را با هم جمع می‌کنیم: $$ \frac {16}{3}+\frac {22}{3}=\frac {38}{3}$$.
در نهایت، عدد کسری را به عدد مخلوط تبدیل می‌کنیم: $$ \frac {38}{3}=\frac {36+2}{3}=\frac {36}{3}+\frac23=12+\frac 23=12\frac 23$$.
تفریق اعداد مخلوط نیز مشابه جمع انجام می‌شود، با این تفاوت که در آن، عمل تفریق را انجام می‌دهیم.
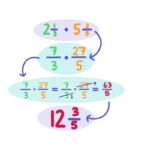
ضرب اعداد مخلوط
ضرب اعداد محلوط کار بسیار ساده‌ای است و برای انجام آن، کافی است ابتدا اعداد مخلوط را، مطابق آنچه در بخش‌های قبل آموختیم، به یک کسر تبدیل کنیم، سپس کسرها را در هم ضرب کنیم. برای ضرب کسرها نیز کافی است صورت را در صورت و مخرج را در مخرج ضرب کنیم. گاهی نیز صورت و مخرج بر هم بخش‌پذیر هستند و می‌توانیم آن‌ها را ساده کنیم.
آنچه را که گفتیم، با یک مثال شرح می‌دهیم. فرض کنید می‌خواهیم دو عدد مخلوط $$ 2 \frac 13 $$ و $$ 3 \frac 1 4 $$ را در هم ضرب کنیم. همان‌طور که گفتیم، ابتدا دو عدد مخلوط را به کسر تبیدل می‌کنیم.
برای عدد $$ 2 \frac 13 $$، داریم:
$$ 2 \frac 13 = \frac {2 \times 3 }{3 } + \frac 13 = \frac 63 +\frac 13 = \frac 7 3 $$
عدد $$ 3 \frac 1 4 $$ نیز این‌گونه به کسر تبدیل می‌شود:
$$ 3 \frac 1 4 = \frac { 3 \times 4 } {4} +\frac 14 = \frac {12} 4 +\frac 14 = \frac {13} 4 $$
اکنون ضرب $$ 2 \frac 13 \times 3 \frac 1 4 $$ به‌شکل زیر درآمده است:
$$ \frac 7 3 \times \frac {13} 4 $$
حال، برای انجام ضرب کافی است صورت را در صورت و مخرج را در مخرج ضرب کنیم:
$$ \frac 7 3 \times \frac {13} 4 = \frac {7 \times 13 } { 3 \times 4 } = \frac { 91 } { 12 } $$
اگر بخواهیم کسر $$ \frac { 91 } { 12 } $$ را به عدد مخلوط تبدیل کنیم، خواهیم داشت:
$$ \frac { 91 } { 12 } = \frac {84 + 7}{12} = \frac {12\times 7 + 7 }{12 } = \frac {12 \times 7 } { 12 } + \frac 7 {12} = 7 + \frac 7 {12} = 7 \frac 7 {12} $$
همان‌طور که مشاهده کردید، ضرب اعداد مخلوط را به‌سادگی انجام دادیم. در ادامه، به ارائه مثال‌هایی از ضرب اعداد مخلوط می‌پردازیم.
یک اشتباه رایج
دانش‌آموزان، هنگام ضرب اعداد ضرب اعداد مخلوط، معمولاً دچار اشتباه رایجی می‌شوند و آن این است که قبل از تبدیل اعداد مخلوط به کسر، بخش‌های صحیح یا همان عددهای کامل را در هم ضرب می‌کنند و برای بخش‌های کسری نیز چنین می‌کنند. برای مثال، فرض کنید می‌خواهیم ضرب دو عدد $$ 3\frac 57 $$ و $$ 4 \frac 12 $$ را انجام دهیم.
اشتباه رایج دانش‌آموزان که غلط است، این‌گونه است:
$$ 3\frac 57 \times 4 \frac 12 =( 3\times 4 )\frac 57 \times \frac 12 = 12 \frac 5 {14} $$
به‌عنوان یک مثال دیگر، برای ضرب $$ 2 \times 3 \frac 12 $$ نیز محاسبه زیر غلط است:
$$ 2 \times 3 \frac 12 =6 \frac 12 $$
دقت کنید که دچار این اشتباه نشوید و همان گام‌هایی را طی کنید که در بخش قبل گفتیم.
ضرب اعداد مخلوط با شکل (روش مساحتی)
یک راه دیگر برای ضرب اعداد مخلوط، استفاده از شکل است که به ن روش مساحتی نیز میگویند. در این روش، از مساحت مستطیل برای محاسبه ضرب استفاده می‌شود، زیرا مستطیل هم دوبعدی است و هم طول و عرض با اندازه غیریکسان دارد.
فرض کنید می‌خواهیم ضرب $$ 3 \frac 15 \times 2 \frac 23 $$ را انجام دهیم. برای محاسبه حاصل‌ضرب این دو عدد مخلوط، یک مستطیل رسم می‌کنیم که طول و عرض آن برابر بر هریک از دو عدد است. همان‌طور که مشاهده می‌کنید، اندازه هر ضلع برابر با مجموع بخش صحیح و بخش کسری عدد مخلوط است.
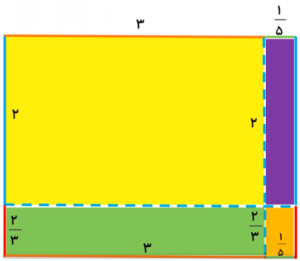
اما حاصل‌ضرب دو عدد مخلوط چگونه به‌دست می‌آید؟ همان‌طور که می‌دانیم، ضرب $$ 3 \frac 15 \times 2 \frac 23 $$ در واقع برابر با مساحت شکل بالاست. بنابراین، برای محاسبه حاصل‌ضرب، کافی است مساحت چهار مستطیل کوچک را به‌دست آوریم و آن‌ها را با هم جمع کنیم:
- مساحت مستطیل زرد: $$ 2 \times 3 = 6 $$
- مساحت مستطیل سبز: $$3\times \frac 23 =2$$
- مساحت مستطیل بنفش: $$2 \times \frac 15=\frac 25 $$
- مساحت مستطیل نارنجی: $$\frac 23 \times \frac 15 = \frac 2 {15}$$
اکنون، مساحت مستطیل بزرگ به‌راحتی قابل محاسبه است:
$$ \begin {align}6 + 2 + \frac 25 +\frac 2 {15} & =8+\frac 25+\frac 2 {15}= 8+\frac {2\times3}{5\times3}+\frac 2 {15}\\ &= 8+\frac 6{15}+\frac 2{15} =8+\frac 8 {15}=8\frac 8 {15}
\end{align}$$
بنابراین، حاصل‌ضرب برابر است با
$$ \begin {align}3 \frac 15 \times 2 \frac 23=8\frac 8 {15}
\end{align}$$
مثال‌های ضرب اعداد مخلوط
در این بخش، مثال‌های متنوعی از ضرب اعداد مخلوط را بیان می‌کنیم.
مثال اول ضرب اعداد مخلوط
دو عدد مخلوط $$ 1 \frac 2 5 $$ و $$ 3 \frac 23 $$ را در هم ضرب کنید.
حل: قبل از هر چیز، ابتدا دو عدد مخلوط را به عددهای کسری تبدیل می‌کنیم:
$$ \begin {align} 1 \frac 2 5 & = \frac {1 \times 5 } { 5 } +\frac 25 = \frac 55 + \frac 25 = \frac {5+2} 5 = \frac 75 \\
3 \frac 23 & = \frac { 3 \times 3 } {3 }+ \frac 2 3 = \frac 9 3 + \frac 23=\frac { 9 + 2 } { 3 } = \frac {11 }{3}
\end {align} $$
اکنون باید ضرب زیر را انجام دهیم:
$$ \frac 75+\frac {11 }{3}= \frac {7 \times 11} { 5 \times 3 } =\frac {77} {15} $$
این عدد را می‌توانیم به‌صورت زیر به یک عدد مخلوط تبدیل کنیم:
$$ \frac {77} {15} = \frac {75+ 2 }{15} = \frac {75}{15}+ \frac 2 {15} = 5 + \frac 2 {15} = 5 \frac 2 {15} $$
مثال دوم ضرب اعداد مخلوط
باغچه احمد $$4$$ و $$\frac 23$$ متر طول و $$1$$ و $$\frac 18 $$ متر عرض دارد. مساحت باغچه او چقدر است؟
حل: برای حل این مثال، باید این دو عدد مخلوط را ضرب کنیم تا مساحت به‌دست آید. بدین منظور، ابتدا هر عدد مخلوط را به کسر تبدیل می‌کنیم:
$$4 \frac { 2 } { 3 } = \frac { 1 4 } { 3 } , \; \;\; 1 \frac { 1 } { 8 } = \frac { 9 } { 8 } $$
سپس آن‌ها را ضرب می‌کنیم.
$$ \frac { 1 4 } { 3 } \times \frac { 9 } { 8 } = \frac { 1 4 \times 9 } { 3 \times 8 } = \frac { 1 4 \times 9 } { 3 \times 8 } = \frac { 7 \times 3 } { 1 \times 4 } = \frac { 2 1 } { 4 } = 5 \frac { 1 } { 4 } $$
بنابراین، مساحت باغچه $$5 \frac { 1 } { 4 } $$ متر مربع است.
مثال سوم ضرب اعداد مخلوط
ضرب $$ 6 \frac { 2 } { 3 } \times 3 \frac {3 } { 1 0 } $$ را انجام دهید.
حل: ابتدا دو عدد مخلوط را به کسر تبدیل می‌کنیم:
$$
6 \frac{2}{3}=\frac{20}{3} \text { , } \;\;\;3 \frac{3}{10}=\frac{33}{10}
$$
سپس آن‌ها را ضرب می‌کنیم:
$$ \frac { 2 0 } { 3 } \times \frac { 3 3 } { 1 0 } = \frac { 2 0 \times 3 3 } { 3 \times 1 0 } = \frac { 2 0 \times 3 3 } { 3 \times 1 0 } = \frac { 2 \times 1 1 } { 1 \times 1 } = \frac { 2 2 } { 1 } = 2 2 $$
دقت کنید که $$ 33 $$ و $$ 3 $$ و همچنین $$ 10 $$ و $$ 20 $$ با هم ساده شده‌اند.
مثال چهارم ضرب اعداد مخلوط
ضرب $$ 4\frac 12 $$ و $$ 7 \frac 14 $$ را به روش مساحتی انجام دهید.
حل: قبل از هر چیز، می‌دانیم که باید یک مستطیل رسم کنیم که طول آن $$ 7 \frac 14 $$ یا $$ 7 + \frac 14 $$ و عرضش $$ 4 \frac 12 $$ یا $$ 4 + \frac 12 $$ است. این شکل در ادامه آورده شده است.
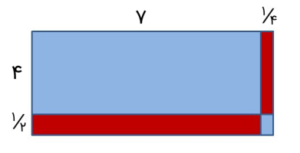
حاصل‌ضرب نیز برابر با جمع چهار مساحت شکل است:
$$
\begin{aligned}
4\frac 12 \times 7 \frac 14 &=(4 \times 7)+(\frac 12 \times 7)+(4 \times \frac 14 )+(\frac 12 \times \frac 14 ) \\
& =28+\frac {7 } 2+1+\frac 1 8 \\ & = 28 + 3\frac 12 + 1 + \frac 18 \\ & = 28+ 3+\frac 12 + 1 + \frac 18 \\ & = 28 + 3+ 1 + \frac 12 + \frac 18 \\ & = 32+\frac 4 8 + \frac 18 \\ & = 32+\frac 58 = 32 \frac 58
\end{aligned}
$$
مثال پنجم ضرب اعداد مخلوط
حاصل جمع و ضرب دو عدد مخلوط $$ 3 \frac 14 $$ و $$2 \frac 13 $$ را محاسبه کنید.
حل: ابتدا جمع دو عدد را محاسبه می‌کنیم:
$$ 3 \frac 14 + 2 \frac 13 $$
برای جمع دو عدد، ابتدا دو عدد صحیح را جمع می‌کنیم:
$$ 3+2 = 5 $$
اکنون نوبت کسرهاست که آن‌ها را با هم جمع کنیم:
$$ \frac 14 + \frac 13 $$
چون که مخرج کسرها یکسان نیست، باید مخرج مشترک بگیریم و آن‌ها را جمع کنیم. کوچک‌ترین مضرب مشترک دو عدد $$3$$ و $$4$$، عدد $$12$$ است که می‌شود مخرج مشترک دو کسر. پس، جمع دو کسر به‌شکل زیر انجام می‌شود:
$$ \frac 14 + \frac 13= \frac {1\times 3}{12}+\frac{1\times 4} {12} = \frac {3+4}{12}= \frac{7}{12}$$
اکنون هم جمع دو عدد صحیح را داریم و هم حاصل‌جمع دو کسر را. بنابراین، جواب نهایی جمع دو عدد مخلوط به‌شکل زیر است:
$$ 3\frac 14 + 2\frac 13= (3+2)+ (\frac 14+\frac 13)= 5 + \frac {7}{12}=5\frac{7}{12}$$
می‌توانیم عدد مخلوط جواب را به یک عدد کسری تبدیل کنیم:
$$ 5\frac{7}{12}=5+\frac {7}{12}=\frac {5\times 12}{12}+\frac {7}{12}=\frac {60}{12}+\frac {7}{12}=\frac {67}{12}$$
حال، ضرب این دو عدد مخلوط را محاسبه می‌کنیم. دقت کنید که ضرب را با جمع اشتباه نگیرید و اعداد صحیح را در هم ضرب نکنید. تنها از روشی استفاده کنید که بیان کردیم. ابتدا دو عدد مخلوط را به کسر تبدیل کنید:
$$ \begin {align} 3 \frac 14 & = \frac {3\times 4}{4}
+ \frac 14 = \frac {12}4 + \frac 14 = \frac {12+1} 4 = \frac {13 } 4 \\ 2 \frac 13 & =\frac {2 \times 3}{3 }+\frac 13 = \frac 6 3 +\frac 1 3 = \frac {6 + 1 } 3 = \frac 7 3 \end {align} $$
در ادامه، این دو کسر را در هم ضرب می‌کنیم:
$$ \begin {align} \frac {13 } 4 \times \frac 7 3 = \frac {13 \times 7 } { 4 \times 3 } = \frac {91}{12}\end {align} $$
اگر بخواهیم کسر $$ \frac { 91 } { 12 } $$ را به عدد مخلوط تبدیل کنیم، خواهیم داشت:
$$ \frac { 91 } { 12 } = \frac {84 + 7}{12} = \frac {12\times 7 + 7 }{12 } = \frac {12 \times 7 } { 12 } + \frac 7 {12} = 7 + \frac 7 {12} = 7 \frac 7 {12} $$
مثال ششم ضرب اعداد مخلوط
ضرب $$ 9 \frac{1}{6} \times 12 \frac{3}{5} $$ را انجام دهید.
حل: ابتدا دو عدد را به کسر تبدیل می‌کنیم:
$$ 9 \frac { 1 } { 6} = \frac{55}{6} \text { , } \;\;\; 12 \frac{3} { 5 } = \frac { 6 3 } { 5 } $$
سپس، ضرب را انجام می‌دهیم:
$$ \frac { 5 5 } { 6 } \times \frac { 6 3 } { 5 } = \frac { 5 5 \times 6 3 } { 6 \times 5 } = \frac { 1 1 \times 2 1 } { 2 \times 1 } = \frac { 2 31 } { 2 } = 115 \frac { 1 } { 2 } $$
مثال هفتم ضرب اعداد مخلوط
ضرب $$ 12 \times 1 \frac{6}{7} $$ را انجام دهید.
حل: دقت کنید که نباید مستقیماً عدد $$ 12$$ را در عدد $$ 1 \frac 6 7 $$ ضرب کنید. ابتدا باید دو عدد را به کسر تبدیل کنیم:
$$ 1 \frac{6}{7} = \frac {1 \times 7 + 6 } {7} = \frac {13} 7 , \;\;\; 12 = \frac {12} 1 $$
در نهایت، ضرب دو کسر را انجام می‌دهیم:
$$
12 \times 1 \frac { 6 } { 7 } = \frac { 1 2 } { 1 } \times \frac { 1 3 } { 7 } = \frac { 1 5 6 } { 7 } = 2 2 \frac{2}{7}
$$
مثال هشتم ضرب اعداد مخلوط
حاصل ضرب زیر را به‌دست آورید:
$$ \frac {1 1 } { 8 } \times 4 \frac { 1 } { 2 } \times 3 \frac { 1 }{ 3 } $$
حل: ابتدا دو عدد مخلوط $$4 \frac { 1 } { 2 } $$ و $$3 \frac { 1 }{ 3 } $$ را به کسر تبدیل می‌کنیم:
$$ 4 \frac { 1 } { 2 } = \frac 9 2 , \;\;\; 3 \frac { 1 }{ 3 } = \frac {10} 3 $$
در ادامه، ضرب را انجام می‌دهیم:
$$ \frac { 1 1 } { 8 } \times 4 \frac { 1 } { 2 } \times 3 \frac { 1 } { 3 } = \frac { 1 1 \times 9 \times 1 0 } { 8 \times 2 \times 3 } = \frac { 1 1 \times 3 \times 5 } { 8 \times 1 \times 1 } = \frac { 1 6 5 } { 8 } = 2 0 \frac { 5 } { 8 } $$
تمرین
در ادامه، چند مورد از ضرب اعداد مخلوط و جواب نهایی آن‌ها را آورده‌ایم. سعی کنید طبق آنچه درباره روش انجام ضرب اعداد مخلوط گفتیم، مراحل را طی کنید و جوابتان را به آنچه آورده‌ایم مقایسه کنید:
$$\begin {aligned}
& 1 \frac { 5 } { 8 } \times 5 \frac { 3 } { 4 } = \frac { 2 9 9 }{ 3 2 } = 9 \frac { 1 1 } { 3 2 } \\
& 1 \frac { 1 } { 4 } \times 2 \frac { 1 } { 3 } = \frac { 3 5 } { 1 2 } = 2 \frac { 1 1 } { 1 2 } \\
& 4 \frac { 3 } { 7 } \times 3 \frac { 3 } { 5 } = \frac { 5 5 8 } { 3 5 } = 1 5 \frac { 3 3 } { 3 5 } \\
& 5 \frac { 1 } { 3 } \times 1 \frac { 3 } { 4 } = \frac { 1 1 2 } { 1 2 } = \frac { 2 8 } { 3 } = 9 \frac { 1 } { 3 } \\
& 2 \frac { 3 } { 5 } \times 2 \frac { 1 } { 7 } = \frac { 1 9 5 } { 3 5 } = \frac { 3 9 } { 7 } = 5 \frac { 4 } { 7 } \\
& 4 \frac { 3 } { 4 } \times 1 \frac { 1 } { 6 } = \frac { 1 3 3 } { 2 4 } = 5 \frac { 1 3 } { 2 4 } \\
& 5 \frac { 1 } { 2 } \times 1 \frac { 1 } { 4 } = \frac { 5 5 } { 8 } = 6 \frac { 7 } { 8 } \\
& 1 \frac { 1 } { 2 } \times 1 \frac { 5 } { 6 } = \frac { 3 3 }{ 1 2 } = \frac { 1 1 } { 4 } = 2 \frac { 3 } { 4 } \\
& 5 \frac { 7 } { 8 } \times 1 \frac { 2 } { 3 } = \frac { 2 3 5 } { 2 4 } = 9 \frac { 1 9 } { 2 4 } \\
& 2 \frac { 4 } { 9 } \times 2 \frac { 5 } { 9 } = \frac { 5 06 } { 8 1 } = 6 \frac { 2 0 } { 8 1 }
\end {aligned} $$
معرفی فیلم آموزش ریاضی پایه هفتم
برای آشنایی بیشتر با مباحث درس ریاضی پایه هفتم، پیشنهاد می‌کنیم فیلم آموزش ریاضی پایه هفتم فرادرس را مشاهده کنید که در ۱۳ ساعت و ۳ دقیقه تدوین شده و همه مباحث 14 درس کتاب درسی را به‌طور کامل پوشش می‌دهد. در فصل یکم این آموزش، راهبردهای حل مسئله معرفی می‌شود. فصل دوم درباره عددهای صحیح است. فصل سوم درباره جبر و معادله است. در فصل چهارم به هندسه و استدلال پرداخته شده است. موضوع فصل ششم سطح و حجم است. در فصل هفتم به توان و جذر پرداخته شده است. فصل هشتم به بردار و مختصات اختصاص یافته است و در نهایت، آمار و احتمال در فصل نهم معرفی می‌شود.
- برای مشاهده فیلم آموزش ریاضی پایه هفتم + اینجا کلیک کنید.
جمع‌بندی
در این آموزش، با روش ضرب اعداد مخلوط آشنا شدیم و مثال‌های متنوعی را حل کردیم.
