زاویه محاطی چیست؟ – اثبات قضیه + حل تمرین و مثال های متنوع
به زاویهای که راس آن بر روی محیط دایره قرار داشته باشد و ضلعهای آن، وترهای دایره را تشکیل دهند، زاویه محاطی میگویند. زاویههای محاطی، برای بسیاری از قضایای هندسی (تالس، قوت یک نقطه و غیره) مورد استفاده قرار میگیرد. این زاویهها، در هنر و معماری نیز کاربرد بسیار گستردهای دارند. در این مقاله، به معرفی زاویه محاطی و محاسبات مرتبط با آن به همراه حل چندین مثال میپردازیم. علاوه بر این، قضیه زاویه محاطی را برای سه حالت مختلف اثبات میکنیم.
زاویه و انواع آن چیست؟
زاویه، شکلی شامل دو نیمخط (ضلع) است که یکدیگر را در یک نقطه (راس) قطع میکنند. یکی از معیارهای تقسیمبندی انواع زاویه، وضعیت قرارگیری اجزای آن (راس و ضلعهای زاویه) نسبت به دایره است.

بر این اساس، زاویهها به انواع زیر تقسیم میشوند:
- زاویه مرکزی
- زاویهای که راس آن، مرکز دایره و ضلعهای آن، دو شعاع دایره است.
- زاویه داخلی
- زاویهای که راس و ضلعهای آن درون دایره قرار دارند.
- زاویه خارجی
- زاویهای که راس آن، خارج از دایره قرار دارد و هر یک از ضلعهای آن، محیط دایره را در دو نقطه قطع میکنند.
- زاویه محیطی
- زاویهای که ضلعهای آن، مماسهای دایره هستند و راس آن، خارج دایره قرار دارد.
- زاویه ظلی
- زاویهای که راس آن روی دایره قرار دارد. یکی از ضلعهای این زاویه، مماس بر دایره و ضلع دیگر آن شامل وتری از دایره میشود.
- زاویه محاطی
در صورت علاقه به یادگیری بیشتر در مورد انواع زاویهها، مطالعه مطلب «انواع زاویه چیست؟ — معرفی تمام زاویهها — به زبان ساده» را به شما پیشنهاد میکنیم.
زاویه محاطی چیست؟
«زاویه محاطی» (Inscribed Angle)، زاویهای است که راس آن، بر روی کمان دایره قرار میگیرد و ضلعهای آن، دو وتر دایره را تشکیل میدهد.
تصویر زیر، نمونهای از یک زاویه محاطی و زاویه مرکزی متناظر را نمایش میدهد. از آنجایی که این دو زاویه، مقابل به کمان AB قرار دارند، اندازه آنها، با توجه به اندازه این کمان مشخص میشود.
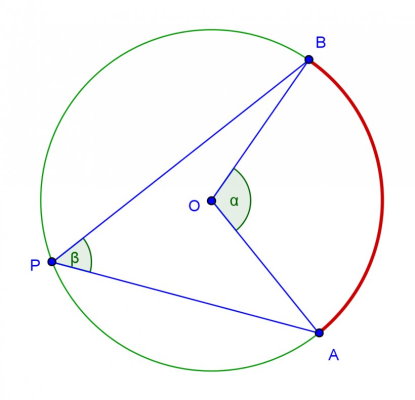
بر اساس تعریف، زاویه APB، یک زاویه محاطی است؛ چراکه راس آن در نقطه P بر روی محیط دایره قرار گرفته و ضلعهای آن، دایره را در نقاط A و B قطع میکنند. اندازه زاویه محاطی بالا برابر با β و اندازه زاویه مرکزی متناظر با آن برابر با α است. این دو اندازه، یک رابطه مشخص با یکدیگر دارند که در بخشهای بعدی، به معرفی و اثبات آن خواهیم پرداخت.
اجزای زاویه محاطی چه هستند؟
زاویههای محاطی نیز مانند دیگر انواع زاویهها، از یک راس و دو ضلع تشکیل میشوند. نکته متمایز در اینجا، کمان مقابل به زاویه محاطی است. تصویر زیر را در نظر بگیرید. این تصویر، چهار پارهخط (وتر) و چهار نقطه بر روی یک دایره را نمایش میدهد.
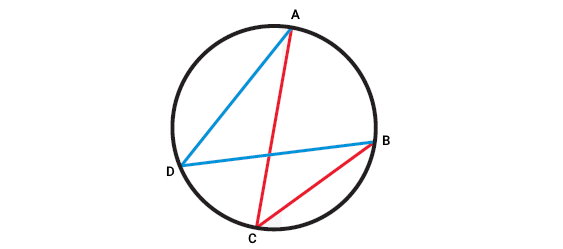
در تصویر بالا، چهار زاویه محاطی وجود دارد. این زاویهها و اجزای آنها عبارت هستند از:
- زاویه CAD
- راس A
- ضلع AD
- ضلع AC
- زاویه CBD
- راس B
- ضلع BD
- ضلع BC
- زاویه ADB
- راس D
- ضلع DA
- ضلع DB
- زاویه ACB
- راس C
- ضلع CA
- ضلع CB
همانطور که مشاهده میکنید، زاویههای CAD و CBD، در مقابل کمان DC قرار میگیرند. به DC، کمان مقابل به زاویه محاطی CAD و CBD میگویند. زاویههای ADB و ACB نیز در مقابل کمان AB قرار دارند. به عبارت دیگر، AB، کمان مقابل به این زاویههای محاطی است.
مثال ۱: تعیین زاویه های محاطی
زاویههای محاطی مقابل به کمان AE را نام ببرید.
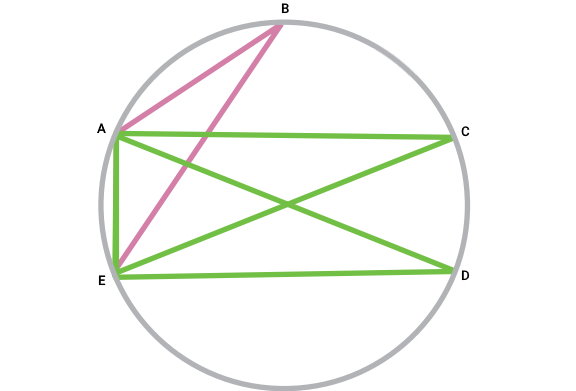
به منظور یافتن زاویههای محاطی، از تعریف آنها کمک میگیریم. در تصویر بالا، پنج نقطه بر روی دایره مشخص شده است. از میان این نقاط، ابتدا باید راسهای زاویههای مورد نظر را پیدا کنیم. A و E، نقاط انتهایی کمان AE هستند و نمیتوان آنها را به عنوان راس زاویه مقابل به کمان AE در نظر گرفت.
به این ترتیب، راسهای C ،B و D باقی میمانند. در ادامه، وضعیت هر یک از این راسها را تشریح میکنیم:
- راس B، توسط پارهخطهای BA و BE به دو انتهای کمان AE متصل شده است. بنابراین، ABE، یک زاویه محاطی مقابل به کمان AE محسوب میشود.
- راس C، توسط پارهخطهای CA و CE به دو انتهای کمان AE متصل شده است. بنابراین، زاویه ACE نیز یک زاویه محاطی به شمار میرود.
- راس D، توسط پارهخطهای DA و DE، به دو انتهای کمان AE متصل میشود. به این ترتیب، زاویه ADE نیز مانند دو زاویه دیگر، محاطی است.
در نتیجه، سه زاویه ACE ،ABE و ADE، زاویههای محاطی مقابل به کمان AE هستند. بر اساس خواص زاویههای محاطی، به دلیل مشترک بودن کمان مقابل این سه زاویه، اندازه آنها نیز با یکدیگر برابر است.
رسم زاویه محاطی چگونه انجام میشود؟
رسم زاویه محاطی، با استفاده از سه نقطه بر روی محیط دایره انجام میگیرد. به این منظور، ابتدا، توسط یک پرگار، دایرهای به مرکز C و شعاع دلخواه رسم میکنیم.
سه نقطه از محیط را به عنوان نقاط تقاطع زاویه محاطی با دایره در نظر میگیریم. پس از علامتگذاری نقاط، آنها را مانند زیر نامگذاری میکنیم (نقاط B ،A و P).
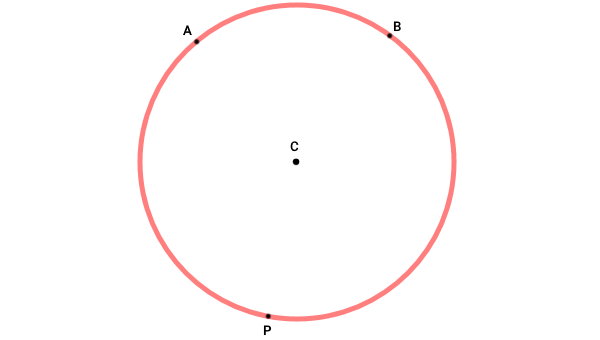
نقطه P را به عنوان راس زاویه محاطی در نظر میگیریم. بهمنظور تشکیل ضلعهای این زاویه، از روی نقطه P، دو پارهخط تا نقاط A و B رسم میکنیم.

با این کار، زاویه APB به وجود میآید. راس این زاویه بر روی محیط دایره قرار دارد. ضلعهای آن نیز محیط دایره را قطع میکنند. از برخورد ضلعهای APB با دایره، کمان AB تشکیل میشود. بنابراین، زاویه APB، یک زاویه محاطی مقابل به کمان AB است. در صورت تمایل به یادگیری نحوه اندازهگیری زاویهها، مطالعه مطالب زیر را به شما پیشنهاد میکنیم:
مثال ۲: رسم چندین زاویه محاطی مقابل به یک کمان
سه زاویه محاطی مقابل به کمان AB رسم کنید.
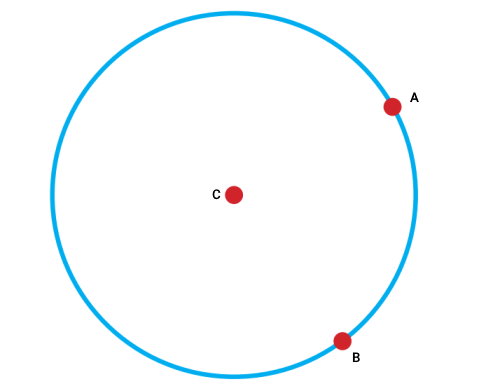
به منظور رسم زاویههای محاطی مقابل به کمان AB، در ابتدا، باید راس هر زاویه را بر روی محیط دایره مشخص کنیم. محل قرارگیری راس میتواند هر نقطهای به غیر از A و B باشد. از اینرو، یک نقطه مانند P را در نظر میگیریم.
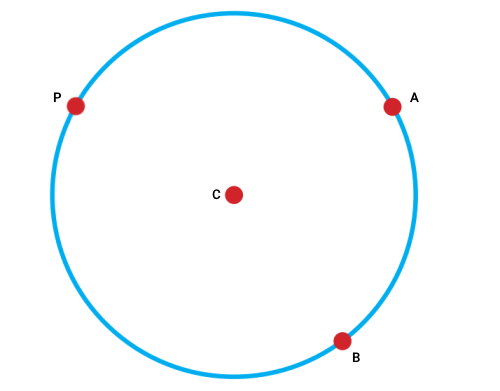
از نقطه P، دو پارهخط تا نقاط A و B رسم میکنیم.
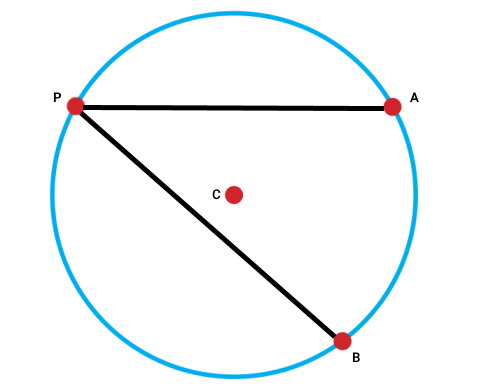
به این ترتیب، یکی از زاویههای محاطی مقابل به کمان AB با عنوان APB ایجاد میشود. دو نقطه دیگر مانند Q و S را مانند تصویر زیر در موقعیتهای دلخواه انتخاب میکنیم.
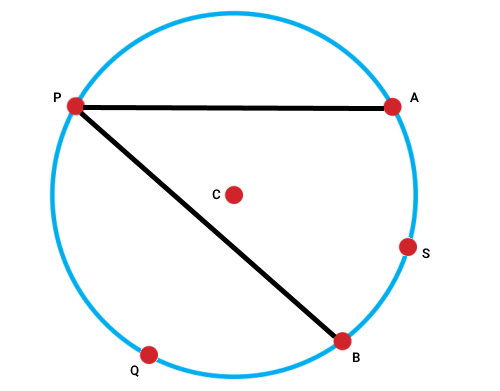
نقاط Q و S را نیز با رسم پارهخط به A و B اتصال میدهیم.
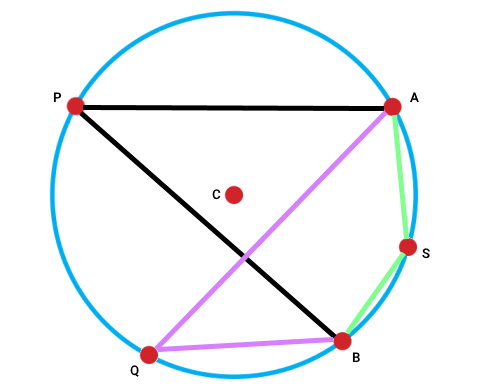
زاویههای AQB و ASB، دیگر زاویههای محاطی مقابل به کمان AB هستند. اکنون سه زاویه محاطی مقابل به کمان AB را داریم. به غیر از این زاویهها، بینهایت زاویه دیگر میتوانیم رسم کنیم که محاطی و روبهروی AB باشند. به نظر شما، اندازه زاویههای مقابل به کمان AB، با یکدیگر ارتباط دارند؟ پاسخ این سوال را در بخش بعدی خواهید یافت.
خواص زاویه های محاطی چه هستند ؟
از خواص و ویژگی های مهم زوایای محاطی میتوان به موارد زیر اشاره کرد:
- زاویههای محاطی مقابل به یک کمان، هماندازه هستند.
- اندازه هر زاویه محاطی، نصف زاویه مرکزی متناظر با آن است.
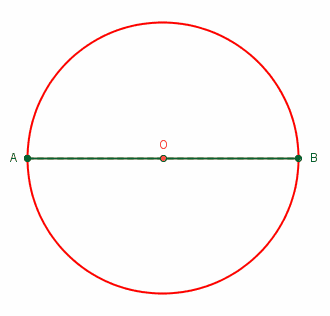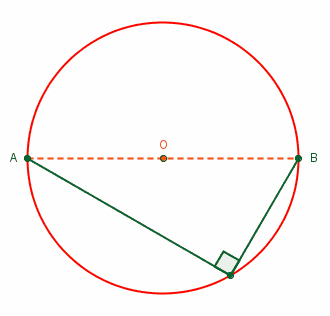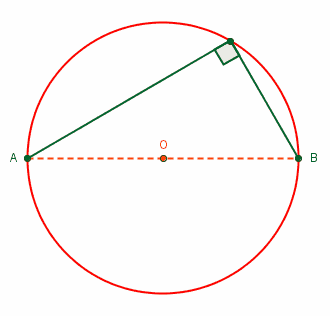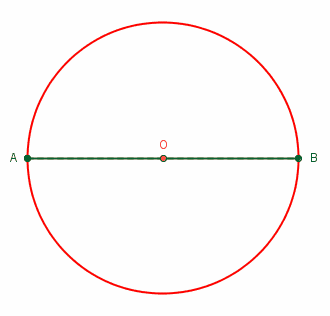
- زاویههای محاطی نیمدایره برابر با ۹۰ درجه هستند.
- جمع دو زاویه داخلی روبهرویی در یک چهارضلعی محاطی، در حالت کلی برابر با ۱۸۰ درجه میشود (اما در حالت خاص ممکن است با هم برابر شوند).
مثال ۳: تعیین زاویه محاطی از روی دیگر زوایای محاطی
اگر زاویه ABE برابر با ۳۰ درجه باشد، اندازه زاویههای ACE و ADE چقدر است؟
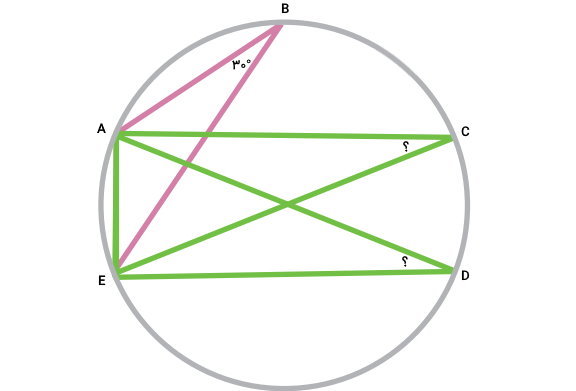
زاویههای ACE ،ABE و ADE، زاویههای محاطی مقابل به کمان AE هستند. بر اساس خواص این ویژگیهای این زاویهها، اندازه آنها با یکدیگر برابر است. بنابراین، اگر زاویه ABE برابر با ۳۰ درجه باشد، اندازه زاویههای ACE و ADE نیز برابر با ۳۰ درجه خواهد بود.
چند ضلعی محاطی چیست ؟
به یک چندضلعی که تمام راسهای آن از روی محیط دایره عبور میکنند، چندضلعی محاطی میگویند. تمام راسهای این نوع چندضلعی، به عنوان یک زاویه محاطی در نظر گرفته میشوند. اگر یک چهارضلعی، محاط در یک دایره باشد، زاویههای روبهرویی آن، هماندازه خواهند بود.
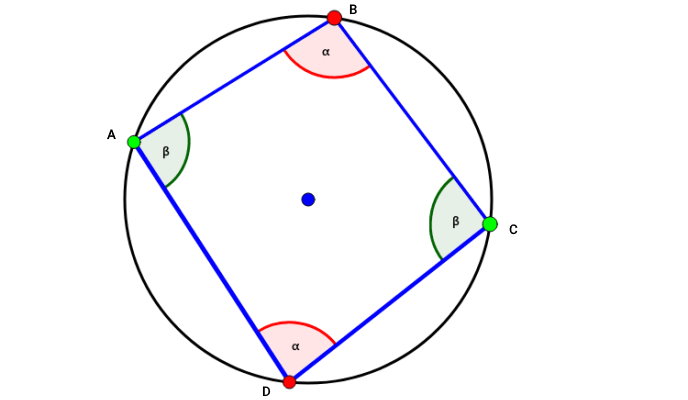
تصویر بالا، نمونهای از یک چهارضلعی محاطی را نمایش میدهد. زاویههای محاطی ABC و CDA، مقابل به کمان AC هستند. بنابراین، اندازه این دو زاویه با هم برابر میشود. بر اساس همین استدلال میتوانیم بگوئیم که اندازه زاویههای BCD و DAB (زاویههای محاطی مقابل به کمان BD) نیز با هم برابرند.
مثال ۴: تعیین زاویه چهارضلعی محاطی
اندازه تمام زاویههای چهارضلعی محاطی زیر را به دست بیاورید.
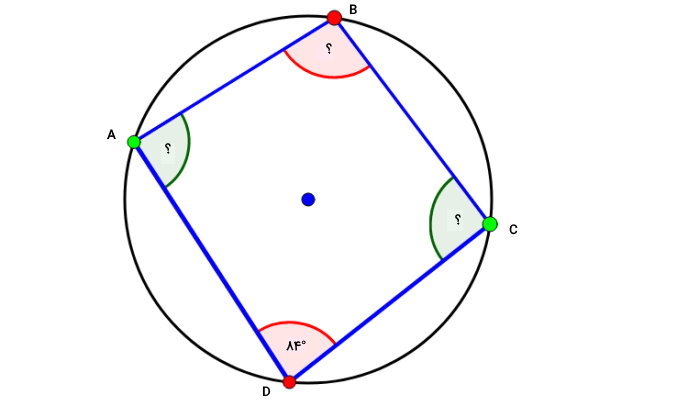
مطابق با شکل بالا، یکی از زاویههای این چهار ضلعی محاطی (زاویه CDA)، برابر با ۸۴ درجه است. بنابراین زاویه مقابل به آن (ABC) نیز برابر با ۸۴ درجه خواهد بود. نکته مهم در محاسبه دو زاویه دیگر، آشنایی با فرمول مجموع زوایای داخلی چندضلعیها است. بر اساس این فرمول، جمع زاویههای یک n ضلعی برابر است با:
- S: مجموع زوایای داخلی
- n: تعداد ضلعها برابر با ۴
بنابراین، مجموع زوایای داخلی چهارضلعی محاطی بالا برابر با ۳۶۰ درجه است. به عبارت دیگر:
اندازه زاویههای معلوم را درون رابطه بالا قرار میدهیم:
زاویههای BCD و DAB مقابل هم هستند. بنابراین، این دو زاویه نیز اندازه برابر دارند. بنابراین، میتوانیم به جای هر یک از این زاویهها، دیگری را در رابطه بالا بنویسیم:
در نتیجه، زاویه BCD و DAB برابر با ۹۶ درجه هستند.
زاویه مرکزی چیست؟
در بخشهای قبلی، با تعریف زاویههای محاطی و رسم آنها آشنا شدیم. مفهوم این نوع زاویه، تفاوتها و شباهتهایی با مفهوم زاویه مرکزی دارد.
«زاویه مرکزی» (Central Angle)، زاویهای است که راس آن بر روی مرکز دایره قرار دارد و ضلعهای آن، شعاع دایره محسوب میشوند.
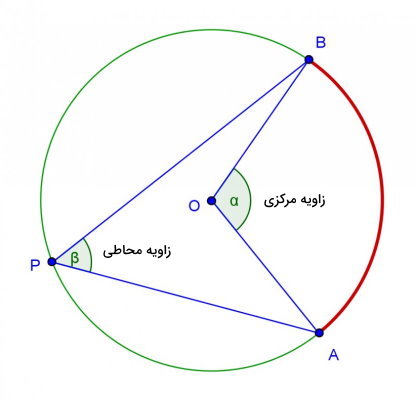
اندازه زاویه مرکزی مقابل به یک کمان، دو برابر زاویه محاطی مقابل به همان کمان است. در تصویر بالا، هر دو زاویه α و β، مقابل به کمان AB هستند. برای این زاویهها داریم:
α = ۲β
به عبارت دیگر، رابطه بین این دو زاویه را میتوان به صورت زیر نوشت:
۲ ÷ β = α
دیگر مطالب مرتبط با انواع زاویهها:
قضیه زاویه محاطی چیست؟
اندازه کمان دایره، هم بر اساس واحد طول و هم بر اساس واحد زاویه بیان میشود. بین زاویه محاطی و کمان روبهروی آن، رابطهای وجود دارد که به آن، «قضیه زاویه محاطی» میگویند. بر اساس این قضیه، اندازه هر زاویه محاطی، برابر با نصف کمان مقابل به آن است.
رابطه بین زاویه کمان دایره و زاویه محاطی مقابل به آن، دقیقا مشابه با رابطه بین زاویه بین زاویه محاطی و زاویه مرکزی متناظر آن است. در بخشهای بعدی، به اثبات خواص زاویه محاطی، از جمله قضیه مربوط به آن خواهیم پرداخت.
مثال ۵: محاسبه زاویه محاطی
تصویر زیر، دایرهای با دو قطر AB و CD و یک وتر AC را نمایش میدهد. اگر زاویه مرکزی مقابل به کمان AC برابر با ۱۰۰ درجه باشد، اندازه زاویههای محاطی BAC و DCA چقدر است؟
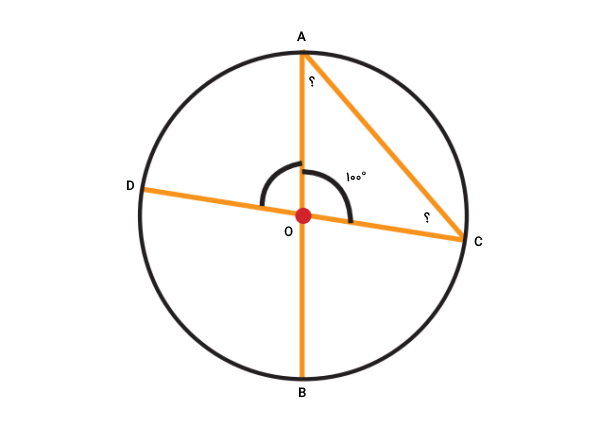
زاویه محاطی DCA، روبهروی کمان AD قرار دارد. بنابراین، اندازه این زاویه، برابر با نصف اندازه زاویه مرکزی روبهروی کمان AD یا همان زاویه AOD است.
از تصویر بالا میتوان دریافت که زاویههای AOC و AOD، مکمل یکدیگر هستند. به عبارت دیگر، جمع این دو زاویه برابر با ۱۸۰ درجه میشود:
اندازه زاویه AOC را درون فرمول بالا قرار میدهیم و آن را برای به دست آوردن زاویه AOD حل میکنیم:
اندازه زاویه مرکزی AOD برابر با ۸۰ درجه است. از اینرو، اندازه کمان مقابل به آن نیز برابر با ۸۰ درجه خواهد بود.
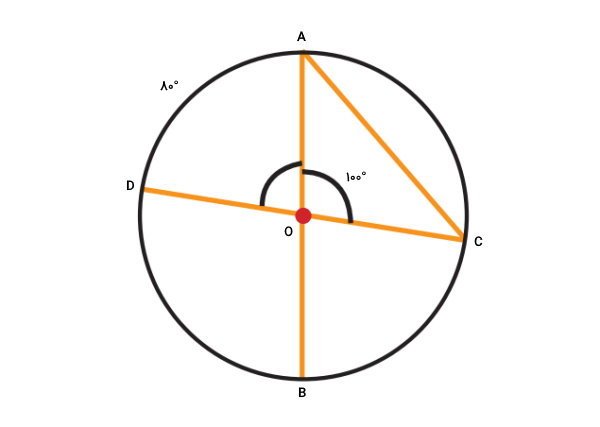
بر اساس رابطه بین زاویه محاطی و کمان مقابل به آن، داریم:
۲ ÷ زاویه کمان = زاویه محاطی
به این ترتیب:
۲ ÷ ۸۰° = زاویه ACD
۴۰° = زاویه ACD
در شکل سوال، یک مثلث به اسم AOC وجود دارد. یکی از زاویههای این مثلث برابر با ۱۰۰ درجه و زاویه دوم آن برابر با ۴۰ درجه است. زاویه OAC یا همان زاویه محاطی BAC، زاویه سوم مثلث AOC محسوب میشود. اندازه این زاویه بر اساس قضیه مجموع زوایای داخلی مثلث به دست میآید:
در نتیجه، اندازه زاویه محاطی BAC برابر با ۴۰ درجه است. البته اگر به شکل مثلث AOC دقت کنید، متوجه خواهید شد که دو ضلع این مثلث، شعاعهای دایره و با اندازههای برابر هستند. بنابراین، زاویههای بین قاعده (AC) و ساقهای این مثلث (OA و OC)، هماندازهاند. در واقع، نیازی به استفاده از قضیه مجموع زوایای داخلی برای تعیین زاویه محاطی BAC نیست.
اثبات رابطه بین زاویه مرکزی و محاطی
اندازه زاویه مرکزی، دو برابر اندازه زاویه محاطی است. این رابطه با عنوان «قضیه زاویه محاطی» (Inscribed Angle Theorem) شناخته میشود. اثبات قضیه زاویه محاطی را برای سه حالت زیر انجام میدهیم:
- قطر دایره، یکی از ضلعهای زاویه محاطی را تشکیل میدهد.
- قطر دایره، بین دو ضلع زاویه محاطی قرار میگیرد.
- قطر دایره، خارج از محدوده ضلعهای زاویه محاطی است.
حالت اول اثبات قضیه زاویه محاطی
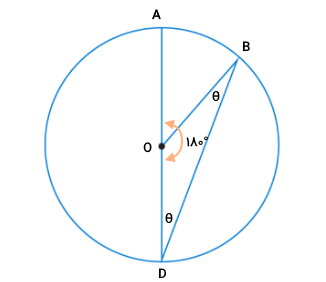
دایرهای به مرکز O را در نظر بگیرید. از روی نقطه A، یکی از قطرهای دایره را رسم میکنیم. این قطر را با عنوان AD نمایش میدهیم. از نقطه D، پارهخطی را به گونهای رسم میکنیم که دایره را در نقطه B قطع کند. زاویه ADB، یک زاویه محاطی مقابل به کمان AB است.
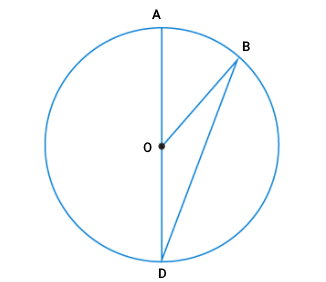
از مرکز دایره در نقطه O، یک پارهخط تا نقطه B میکشیم. این پارهخط، یکی از شعاعهای دایره خواهد بود. زاویه AOB، یک زاویه مرکزی مقابل به کمان AB است. در اینجا قصد داریم ثابت کنیم که زاویه AOB، دو برابر زاویه ADB میشود:
به منظور اثبات رابطه بالا، مثلث OBD را در نظر بگیرید

این مثلث، از نوع متساویالساقین است؛ چراکه ضلعهای OD و OB، شعاع دایره محسوب میشوند و اندازههای برابر دارند:
در مثلثهای متساویالساقین، دو زاویه بین ساق و قاعده، اندازه برابر دارند. به عبارت دیگر، زاویههای ODB و DBO، هماندازه هستند. این زاویهها را با متغیر θ نمایش میدهیم.
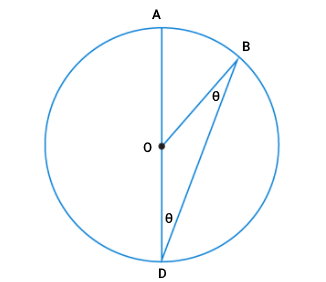
قطر AD، یک زاویه نیمصفحه است. بنابراین، جمع دو زاویه AOB و BOD برابر با ۱۸۰ درجه میشود.
این رابطه را به صورت زیر مینویسیم:
زاویه AOB را برابر با متغیر x در نظر میگیریم:
بر اساس قضیه جمع زوایای داخلی مثلث، مجموع زاویههای مثلث OBD برابر با ۱۸۰ درجه میشود:
به جای عنوان هر یک از زاویهها، متغیرهای مربوط به آنها را در رابطه بالا جایگزین میکنیم:
با سادهسازی رابطه بالا، به نتیجه زیر میرسیم:
x زاویه مرکزی AOB و θ، زاویه محاطی ODB است. بنابراین، در این حالت، ثابت کردیم که اندازه زاویه مرکزی، دو برابر زاویه محاطی میشود.
حالت دوم اثبات قضیه زاویه محاطی
دایرهای به مرکز C را در نظر بگیرید. از روی نقطهای به اسم D، دو وتر دایره را به گونهای رسم میکنیم که قطر دایره در بین دو وتر قرار گیرد. یکی از وترها را با عنوان AD و وتر دیگر را با عنوان BD مشخص میکنیم.
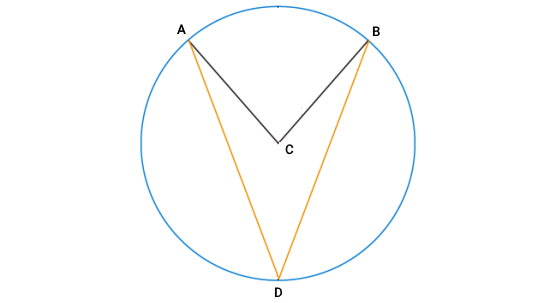
سپس، دو شعاع دایره را از نقطه C تا نقاط A و B میکشیم. به این ترتیب، شعاعهای AC و BC ایجاد میشوند. زاویه ACB، یک زاویه مرکزی مقابل به کمان AB و زاویه ADB، یک زاویه محاطی مقابل به کمان AB است. از آنجایی که هر دوی این زاویهها، روبهرویی کمان AB قرار دارند، میخواهیم اثبات کنیم که اندازه زاویه ACB، دو برابر زاویه ADB است. به این منظور، از روی نقطه D، قطر دایره را رسم میکنیم.
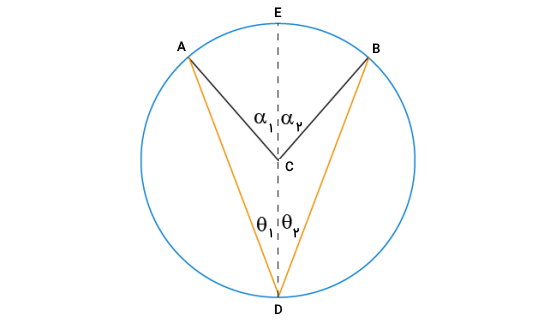
قطر DE، زاویه مرکزی ACB را به دو زاویه α۱ و α۲ تقسیم میکند. به همین ترتیب، زاویه محاطی ADB نیز به دو زاویه β۱ و β۲ تقسیم میشود. بر اساس حالت اول اثبات قضیه زاویه محاطی، میدانیم:
دو رابطه بالا را با هم جمع میکنیم:
در نتیجه، زاویه مرکزی ACB، دو برابر زاویه محاطی ADB است.
حالت سوم اثبات قضیه زاویه محاطی
دایرهای به مرکز C را در نظر بگیرید. از روی نقطهای به نام D، دو وتر دایره را به گونهای رسم میکنیم که قطر گذرنده از نقطه D، خارج از محدوده این دو وتر قرار داشته باشد. وترهای رسم شده را با عنوان AD و BC مشخص میکنیم. زاویه ADB، زاویه محاطی مقابل به کمان AB است.
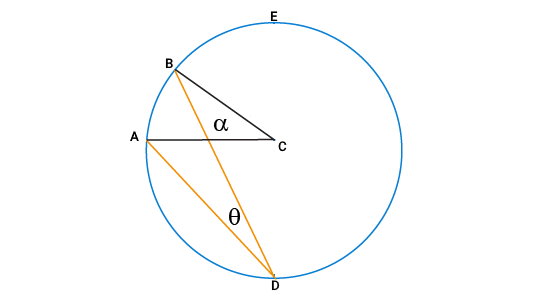
از مرکز دایره، دو شعاع گذرنده از نقاط A و B را رسم میکنیم. به این ترتیب، زاویه مرکزی ACB تشکیل میشود. این زاویه، روبهروی کمان AB قرار دارد. اندازه زاویه محاطی ABD را با حرف θ و اندازه زاویه مرکز ACB را با حرف α مشخص میکنیم. قصد داریم اثبات کنیم که α، دو برابر θ است. به این منظور، قطر دایره را از نقطه D میکشیم.
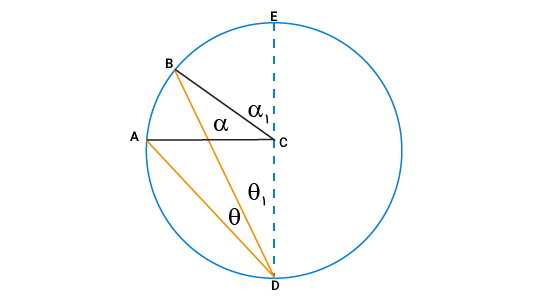
زاویه مرکزی ECB و زاویه محاطی EDB، مقابل به کمان EB قرار دارند. بر اساس حالت اول اثبات قضیه زاویههای محاطی، داریم:
زاویه مرکزی ACE و زاویه محاطی ADE نیز مقابل به کمان AE قرار دارند. از اینرو، رابطه بین اندازه آنها به صورت زیر نوشته میشود:
این رابطه را باز میکنیم:
به جای α۱، معادل آن (۲θ۱) را قرار میدهیم:
۲θ۱ در هر دو طرف معادله قرار دارد. بنابراین، میتوانیم آن را از هر دو طرف حذف کنیم. با این کار، به رابطه زیر میرسیم:
در نتیجه، زاویه مرکزی ACB، دو برابر زاویه محاطی ADB است.
سوالات متداول در رابطه با زاویه محاطی
در این بخش، به تعدادی از پرسشهای پرتکرار در رابطه با زاویههای محاطی به طور مختصر پاسخ میدهیم.
تعریف زاویه محاطی در هندسه چیست ؟
زاویه محاطی، زاویهای است که راس آن روی دایره و اضلاع آن شامل دو وتر از دایره باشند.
اندازه هر زاویه محاطی برابر با چیست ؟
اندازه هر زاویه محاطی برابر با نصف کمان روبهروی آن است.
اندازه کمان روبروی زاویه محاطی چند است ؟
اندازه کمان روبروی زاویه محاطی، دو برابر اندازه آن زاویه است.
چند زاویه محاطی می توان درون یک دایره رسم کرد؟
بیشمار.
زاویه محاطی روبروی قطر چند درجه است ؟
۹۰ درجه. زاویه محاطی روبهروی قطر با عنوان زاویه محاطی قائمه نیز شناخته میشود.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «زاویه ها و انواع آن ها – هر آنجه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- زاویه چیست؟ — تعریف، انواع و اندازه گیری
- انواع زاویه چیست ؟ — معرفی تمام زاویه ها — به زبان ساده
- راس زاویه چیست ؟ — به زبان ساده + حل مثال تصویری
- زاویه حاده چیست ؟ — به زبان ساده + حل مثال های متنوع تصویری
- زاویه باز چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه قائمه چیست ؟ — به زبان ساده + حل مثال های تصویری
- زاویه مکمل چیست ؟ — به زبان ساده + حل تمرین و مثال
- زاویه متمم چیست ؟ — به زبان ساده
- زاویه متقابل به راس چیست ؟ — به زبان ساده + حل تمرین و مثال
- زاویه های مکمل و متمم در هندسه — به زبان ساده
- زاویه نیمصفحه و تعریف آن در هندسه — به زبان ساده
- زاویه محاطی چیست ؟ — اثبات قضیه + حل تمرین و مثال های متنوع(همین مطلب)
- نیمساز چیست ؟ — به زبان ساده
- اندازه گیری زاویه با نقاله — به زبان ساده + مثال های تصویری
- اندازه گیری زاویه با گونیا — به زبان ساده + مثال های تصویری













در مورد زوایای روبرو در چهارضلعی محاطی اشتباه میکنید، در حالت خاص باهم برابرند در حالت کلی مجموع زاوایای روبرو به هم ۱۸۰ درجه خواهد بود
با سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات لازم در متن اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
اندازه زاویه های روبروی یک چهارضلعی محیطی مکمل هم هستند نه برابر!
با سلام و وقت بخیر؛
در این مقاله، زاویههای روبهرویی چهارضلعی محاطی مورد بحث قرار گرفتهاند.
از همراهی شما با مجله فرادرس سپاسگزاریم