حل معادله درجه دو به روش دلتا با مثال و تمرین – به زبان ساده

معادلات درجه دو، از مهم‌ترین معادلات ریاضی هستند برای اهمیت و کاربرد بسیار گسترده‌ای در دنیای واقعی دارند. به دلیل اهمیت بالای این معادلات، تا کنون روش‌های مختلفی برای محاسبه آن‌ها ارائه شده است. یکی از این روش‌ها، روش دلتا نام دارد. حل معادله درجه دو به روش دلتا، با استفاده ضرایب ثابت معادله و یک فرمول مخصوص انجام می‌شود. برخلاف روش‌های دیگر نظیر فاکتورگیری، در روش دلتا، نیازی به تغییر معادله و به‌کارگیری خلاقیت نیست. در این مطلب از مجله فرادرس، نحوه حل معادله درجه دو به روش دلتا را به طور کامل و به همراه چندین مثال و تمرین متنوع آموزش می‌دهیم. علاوه بر این، به معرفی یک روش مشابه با عنوان روش دلتا پریم می‌پردازیم.

معادله درجه دو چیست؟

«معادله درجه دو» (Second-Degree Equation) یا «معادله مربعی» (Quadratic Equation)، یکی از انواع چندجمله‌ای‌ها است که به فرم زیر نوشته می‌شود:

$$ a x ^ ۲ + b x + c = ۰ $$

در این معادله، b ،a و c، ثابت‌های عددی هستند. شرط درجه بودن معادله بالا، صفر نبودن ثابت a یا $$ a \ne ۰ $$ است.

معادله‌های درجه دو، از مهم‌ترین معادلات ریاضی به شمار می‌روند برای توصیف روابط فیزیکی، مطالعه رفتار اشیا و طراحی وسایل در دنیای واقعی مورد استفاده قرار می‌گیرند. به همین دلیل، روش‌های حل این نوع معادله، معمولا در دوران دبیرستان به دانش‌آموزان رشته‌های مختلف آموزش داده می‌شود.

روش های حل معادله درجه دو چه هستند؟

منظور از حل معادله درجه دو، به دست آوردن ریشه‌های این معادله است. در واقع، با حل معادله درجه دو، مقادیری از متغیر x را محاسبه می‌کنیم که به ازای آن‌ها، جواب معادله برابر با صفر می‌شود. روش‌های مختلفی برای حل معادله درجه دو وجود دارد که از متداول‌ترین آن‌ها می‌توان به موارد زیر اشاره کرد:

• حل معادله درجه دو به روش دلتا و ریشه گیری
• حل معادله درجه دو به روش مربع کامل
• حل معادله درجه دو به روش هندسی
• حل معادله درجه دو به روش فاکتورگیری و تجزیه
• حل معادله درجه دو با استفاده از ماشین‌حساب آنلاین

روش دلتا و ریشه‌گیری، یکی از پرکاربردترین و رایج‌ترین روش‌های حل معادله درجه دو به شمار می‌رود. در ادامه این مطلب از مجله فرادرس، این روش را به طور کامل و به همراه حل چندین مثال متنوع آموزش می‌دهیم.

آموزش حل معادله درجه دو به روش دلتا و ریشه گیری

برای یادگیری حل معادله درجه ۲ به روش دلتا، ابتدا فرم کلی معادلات درجه دو را در نظر بگیرید:

$$ a x ^ ۲ + b x + c = ۰ $$

به منظور تعیین ریشه‌های معادله بالا می‌توانیم از فرمول زیر استفاده کنیم:

$$
x = \frac { - b \pm \sqrt { b ^ ۲ - ۴ a c } }{ ۲ a }
$$

به عبارت زیر رادیکال در فرمول بالا، «دلتا» (Delta) می‌گویند و آن را با حرف یونانی دلتا نمایش می‌دهند:

$$ \Delta = b ^ ۲ - ۴ a c $$

با توجه به رابطه بالا می‌توانیم فرمول محاسبه ریشه‌های معادله درجه دو را به صورت زیر بازنویسی کنیم:

$$
x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a }
$$

علامت دلتا، اهمیت بالایی در تشخیص ماهیت معادلات درجه دو و امکان حل آن‌ها دارد. در مجموع، اگر ضرایب ثابت در یک معادله درجه دو را داشته باشیم، می‌توانیم ریشه‌های آن را با استفاده از فرمول‌های بالا به دست بیاوریم. البته یک حالت خاص وجود دارد که در بخش‌های بعدی به معرفی آن خواهیم پرداخت.

مثال ۱: محاسبه ریشه های معادله درجه ۲

می‌خواهیم ریشه‌های معادله درجه دو $$ ۲ x ^ ۲ + ۵ x - ۳ = ۰ $$ را محاسبه کنیم. به این منظور، ابتدا فرمول حل معادله درجه ۲ به روش دلتا را می‌نویسیم:

$$
x = \frac { - b \pm \sqrt { b ^ ۲ - ۴ a c } }{ ۲ a }
$$

بر اساس این فرمول، داریم:

$$ a = ۲ $$

$$ b = ۵ $$

$$ c = - ۳ $$

مقادیر بالا را درون فرمول قرار می‌دهیم:

$$
x = \frac { - ۵ \pm \sqrt { ۵ ^ ۲ - ( ۴ \times ۲ \times - ۳ ) } }{ ۲ \times ۲ }
$$

$$
x = \frac { - ۵ \pm \sqrt { ۲۵ - ( - ۲۴ ) } }{ ۴ }
$$

$$
x = \frac { - ۵ \pm \sqrt { ۴۹ } }{ ۴ }
$$

به دلیل وجود علامت مثبت و منفی، رابطه بالا را یک بار برای $$ x _ ۱ $$ با علامت مثبت و یک بار برای $$ x _ ۲ $$ با علامت منفی حل می‌کنیم:

$$
x _ ۱ = \frac { - ۵ + \sqrt { ۴۹ } }{ ۴ }
$$

$$
x _ ۲ = \frac { - ۵ - \sqrt { ۴۹ } }{ ۴ }
$$

$$
x _ ۱ = \frac { - ۵ + ۷}{ ۴ }
$$

$$
x _ ۲ = \frac { - ۵ - ۷ }{ ۴ }
$$

$$
x _ ۱ = \frac { ۲ }{ ۴ }
$$

$$
x _ ۲ = \frac { - ۱۲ }{ ۴ }
$$

$$
x _ ۱ = \frac { ۱ }{ ۲ }
$$

$$
x _ ۲ = - ۳
$$

به این ترتیب، ریشه‌های معادله درجه دو $$ ۲ x ^ ۲ + ۵ x - ۳ = ۰ $$، برابر با $$ \frac { ۱ }{ ۲ } $$ و $$ - ۳ $$ شد. در این این مثال، یک نکته مهم وجود داشت. همان‌طور که مشاهده کردید، عدد زیر رادیکال در حین محاسبه ریشه‌ها، یک عدد مثبت بود (دلتا، یک عدد حقیقی مثبت بود). شاید برایتان این سوال پیش بیاید که اگر عدد زیر رادیکال برابر با صفر یا یک عدد منفی می‌بود، روش حل معادله چگونه می‌شد. در بخش بعدی، با بررسی حالت‌های مختلف حل معادله درجه ۲، به این سوال پاسخ می‌دهیم.

حالت های مختلف حل معادله درجه دو به روش دلتا

یکی از مهم‌ترین نکاتی که باید در حین حل معادله درجه به روش دلتا به آن دقت داشته باشید، علامت عدد زیر رادیکال یا همان علامت دلتا است. علامت دلتا، باعث به وجود آمدن حالت‌های مختلف برای حل معادله درجه ۲ می‌شود.

برای بررسی این حالت‌ها، فرم کلی معادله درجه و فرمول حل آن را در نظر بگیرید:

$$ a x ^ ۲ + b x + c = ۰ $$

$$
x = \frac { - b \pm \sqrt { b ^ ۲ - ۴ a c } }{ ۲ a }
$$

در این روابط، چند نکته وجود دارد. برای جواب داشتن فرمول محاسبه ریشه‌های معادله درجه دو، مخرج آن نباید برابر با صفر باشد. به عبارت دیگر:

$$ ۲ a \ne ۰ \to a \ne ۰ $$

بر اساس تعریف ارائه شده در ابتدای مقاله، می‌دانیم که ضریب $$ a $$ در معادله درجه دو، یک عدد غیرصفر است. زیر اگر این ضریب برابر با صفر باشد، معادله، دیگر درجه دو نخواهد بود. بنابراین، این شرط (غیرصفر بودن مخرج کسر) همواره برقرار است.

شرط دوم برای جواب داشتن فرمول محاسبه ریشه‌های معادله درجه دو، غیرمنفی بودن عدد زیر رادیکال یا همان دلتا است. اگر دلتا برابر با یک عدد منفی باشد، خروجی رادیکال، یک عدد موهومی یا عدد مختلط خواهد بود. بنابراین، قوانین محاسبه اعداد حقیقی در آن صدق نمی‌کند.

به طور کلی، دلتا می‌تواند یکی از سه حالت زیر را داشته باشد:

• دلتای مثبت ($$ \Delta \gt ۰ $$): معادله درجه ۲، دو ریشه حقیقی دارد.
• دلتای صفر ($$ \Delta = ۰ $$): معادله درجه ۲، یک ریشه حقیقی (ریشه مضاعف) دارد.
• دلتای منفی ($$ \Delta \lt ۰ $$): معادله درجه ۲، ریشه حقیقی ندارد اما دو ریشه مختلط با اعداد موهومی دارد.

در ادامه، حل معادله درجه دو به روش دلتا را برای هر یک از حالت‌های بالا، با حل مثال بررسی می‌کنیم.

مثال ۲: حل معادله درجه دو با دلتای مثبت

حالت کلی و عمومی حل معادله درجه ۲ به روش دلتا، زمانی است که علامت عبارت $$ b ^ ۲ - ۴ a c $$، مثبت شود. اگر دلتا مثبت باشد، می‌توانیم دو جواب حقیقی را به عنوان ریشه‌های معادله درجه دو به دست بیاوریم. به عنوان مثال، معادله $$ x ^ ۲ - x - ۶ = ۰ $$ را در نظر بگیرید. پیش از شروع ریشه گیری از این معادله درجه دو، مقدار دلتا را محاسبه می‌کنیم:

$$ \Delta = b ^ ۲ - ۴ a c $$

برای این مثال، داریم:

$$ a = ۱ $$

$$ b = - ۱ $$

$$ c = ۶ $$

بنابراین:

$$
\Delta = ( - ۱ ) ^ ۲ - ( ۴ \times ۱ \times - ۶ )
$$

$$
\Delta = ۱ - ( -۲۴ )
$$

$$
\Delta = ۱ + ۲۴
$$

$$
\Delta = ۲۵
$$

همان‌طور که مشاهده می‌کنید، دلتا، یک عدد با علامت مثبت است. بنابراین، معادله $$ x ^ ۲ - x - ۶ = ۰ $$، دو ریشه حقیقی خواهد داشت. این ریشه‌ها، با استفاده از فرمول زیر تعیین می‌شوند:

$$ x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a } $$

$$
x = \frac { - ( - ۱ ) \pm \sqrt { ۲۵ } }{ ۲ \times ۱ }
$$

$$
x = \frac { ۱ \pm ۵ }{ ۲ }
$$

$$
x _ ۱ = \frac { ۱ + ۵ }{ ۲ } = \frac { ۶ }{ ۲ } =۳
$$

$$
x _ ۲ = \frac { ۱ - ۵ }{ ۲ } = \frac { - ۴ }{ ۲ } = - ۲
$$

در نتیجه، ریشه‌های معادله درجه دو $$ x ^ ۲ - x - ۶ = ۰ $$ برابر با دو عدد حقیقی $$ ۳ $$ , $$ - ۲ $$ است. اگر کنجکاو هستید بدانید در صورت صفر بودن دلتا، چه تغییری در محاسبه ریشه‌های معادله درجه دو رخ می‌دهد، مثال بعدی را مطالعه کنید.

مثال ۳: حل معادله درجه دو با دلتای صفر

در صورت صفر شدن دلتای یک معادله درجه دو، عبارت رادیکالی از صورت فرمول محاسبه ریشه‌های معادله حذف می‌شود. به این ترتیب، علامت مثبت و منفی پشت رادیکال، دیگر تاثیری بر روی محاسبات نمی‌گذارد. بنابراین، تنها یک جواب حقیقی به دست می‌آید. به عنوان مثال، معادله $$ x ^ ۲ - ۶ x + ۹ = ۰ $$ را در نظر بگیرید. دلتای این معادله برابر است با:

$$ \Delta = b ^ ۲ - ۴ a c $$

$$ a = ۱ $$

$$ b = - ۶ $$

$$ c = ۹ $$

$$
\Delta = ( - ۶ ) ^ ۲ - ( ۴ \times ۱ \times ۹ )
$$

$$
\Delta = ۳۶ - ۳۶
$$

$$
\Delta = ۰
$$

دلتای معادله مورد نظر برابر با صفر شد. از این‌رو، انتظار داریم این معادله، فقط یک ریشه حقیقی داشته باشد. برای اثبات این موضوع، ریشه‌های معادله را با استفاده از فرمول زیر به دست می‌آوریم:

$$ x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a } $$

$$
x = \frac { - ( - ۶ ) \pm \sqrt { ۰ } }{ ۲ \times ۱ }
$$

$$
x = \frac { ۶ \pm ۰ }{ ۲ }
$$

$$
x = \frac { ۶}{ ۲ }
$$

$$
x = ۳
$$

در نتیجه، جواب معادله درجه دو $$ x ^ ۲ - ۶ x + ۹ = ۰ $$ برابر با عدد $$ ۳ $$ شد. در این معادله ریشه دومی وجود نداشت. به عبارت دیگر، ریشه اول و دوم با یکدیگر برابر شدند. در معادله‌های درجه دویی که مانند این مثال، تنها یک ریشه حقیقی داشته باشند، معادله درجه دو با «ریشه مضاعف» (Double Root) می‌گویند. تا به اینجای این مطلب از مجله فرادرس، حل معادله درجه دو به روش دلتا را برای دو حالت بررسی کردیم. در بخش بعدی، آخرین و پیچیده‌ترین حالت از حل معادلات درجه ۲ به روش دلتا را آموزش می‌دهیم.

مثال ۴: حل معادله درجه دو با دلتای منفی

در مجموعه اعداد حقیقی، هیچ عددی را نمی‌توان پیدا کرد که حاصل‌ضرب آن در خودش برابر با یک عدد منفی شود. بنابراین و بر اساس سیستم اعداد حقیقی، رادیکال یک عدد منفی، هیچ جوابی ندارد. به عنوان مثال، رادیکال زیر را در نظر بگیرید:

$$ \sqrt { - ۴ } $$

به دلیل عدم وجود جواب حقیقی برای این رادیکال، ریاضی‌دانان، مفهومی با عنوان «عدد موهومی» (Imaginary Number) را ارائه کردند که به صورت زیر تعریف می‌شود:

$$ i = \sqrt { - ۱ } $$

بر اساس مفهوم عدد موهومی داریم:

$$
\sqrt { - ۴ } = \sqrt { ۴ \times - ۱ } = \sqrt { ۴ } \times \sqrt { - ۱ } = ۲ i
$$

با این پیش‌زمینه، به سراغ حل مثال معادله درجه دو با دلتای منفی می‌رویم. معادله $$ x ^ ۲ + ۴x + ۵ = ۰ $$ را در نظر بگیرید. دلتای این معادله برابر است با:

$$ \Delta = b ^ ۲ - ۴ a c $$

$$ a = ۱ $$

$$ b = ۴ $$

$$ c = ۵ $$

$$ \Delta = ۴ ^ ۲ - ( ۴ \times ۱ \times ۵ ) $$

$$
\Delta = ۱۶ - ( ۲۰ )
$$

$$
\Delta = - ۴
$$

دلتای معادله مورد نظر، عددی با علامت منفی است. بنابراین، این معادله، هیچ جواب حقیقی نخواهد داشت. البته، بر اساس مفهوم اعداد موهومی می‌توانیم ریشه‌های آن را به صورت زیر محاسبه کنیم:

$$ x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a } $$

$$
x = \frac { - ۴ \pm \sqrt { - ۴ } }{ ۲ \times ۱ }
$$

$$
x = \frac { - ۴ \pm ۲ i }{ ۲ }
$$

$$
x _ ۱ = \frac { - ۴ + ۲ i }{ ۲ } = \frac { ۲ ( - ۲ + i ) }{ ۲ } = - ۲ + i
$$

$$
x _ ۲ = \frac { - ۴ - ۲ i }{ ۲ } = \frac { ۲ ( - ۲ - i ) }{ ۲ } = - ۲ - i
$$

به این ترتیب، دو ریشه غیرحقیقی معادله درجه دو $$ x ^ ۲ + ۴x + ۵ = ۰ $$ را به دست آوریم. این دو ریشه ($$ - ۲ + i $$ و $$ - ۲ - i $$)، اعداد مختلط هستند.

حل آنلاین معادله درجه دو به روش دلتا

ابزارهای آنلاین زیادی برای حل معادله درجه دو به روش دلتا وجود دارند. از بهترین وب‌سایت‌های موجود برای انجام این کار می‌توان به موارد زیر اشاره کرد:

• • «ولفرام آلفا» (Wolfram Alpha) (+)
  • «سیمبولب» (Symbolab) (+)
  • «مَث سالور» (Math Solver) (+)

• «مَث‌وِی» (Mathway) (+)

تمام ابزارهای معرفی شده، از بهترین ابزارهای حل مسائل ریاضی با هوش مصنوعی به شمار می‌روند. به عنوان مثال، وب‌سایت سیمبولب را در نظر بگیرید. پس از ورود به صفحه اصلی این وب‌‌سایت، با رابط کاربری زیر روبه‌رو می‌شوید.

در این صفحه، کادری برای نوشتن معادله وجود دارد. البته با کلیک بر روی آیکون کیبورد در انتهای سمت راست این کادر، کلیدهای کمکی برای نوشتن راحت‌تر معادلات به نمایش درمی‌آیند.

برای شروع، معادله درجه دو $$ x ^ ۲ + ۲ x - ۳ = ۰ $$ را درون کادر مربوطه می‌نویسیم.

با کلیک بر روی دکمه «Go» یا فشردن کلید «Enter»، سیبمولب، معادله درجه دو را به روش دلتا حل می‌کند و ریشه‌های آن را به همراه روش حل نمایش می‌دهد.

همان‌طور که مشاهده می‌کنید، معادله $$ x ^ ۲ + ۲ x - ۳ = ۰ $$ دارای دو ریشه حقیقی $$ ۱ $$ و $$ - ۳ $$‌ است. از قابلیت‌های جذاب و کاربردی سیمبولب می‌توان به امکان انتخاب روش حل اشاره کرد. برای حل این مثال، گزینه مقابل «Solve by» بر روی «Quadratic formula» قرار داشت. بنابراین، روش حل نمایش داده شده، همان روش دلتا بود. سیمبولب، امکان حل معادله درجه دو به روش‌های مربع کامل و فاکتورگیری را نیز فراهم کرده است. علاوه بر این قابلیت‌ها، اگر به انتهای مراحل حل بروید، می‌توانید نمودار معادله را نیز مشاهده کنید.

به منظور نمایش بیشتر قابلیت ابزارهای آنلاین در حل معادله درجه دو به روش دلتا، معادله $$ x ^ ۲ - ۴x + ۴ = ۰ $$ را درون کادر تایپ فرمول می‌نویسیم و کلید Enter را فشار می‌دهیم.

همان‌طور که مشاهده می‌کنید، معادله $$ x ^ ۲ - ۴x + ۴ = ۰ $$، فقط یک ریشه حقیقی یا ریشه مضاعف دارد که برابر با $$ ۲ $$ است. اکنون، معادله درجه دو $$ x ^ ۲ - ۲ x + ۷ = ۰ $$ را در نظر بگیرید. دلتای این معادله، برابر با یک عدد منفی است. می‌خواهیم ببینیم آیا ابزارهای آنلاین، قادر به محاسبه ریشه‌های مختلط و غیرحقیقی معادلات درجه دو هستند. به این منظور، معادله مورد نظر را در کادر مربوطه می‌نویسیم و دکمه Go را انتخاب می‌کنیم.

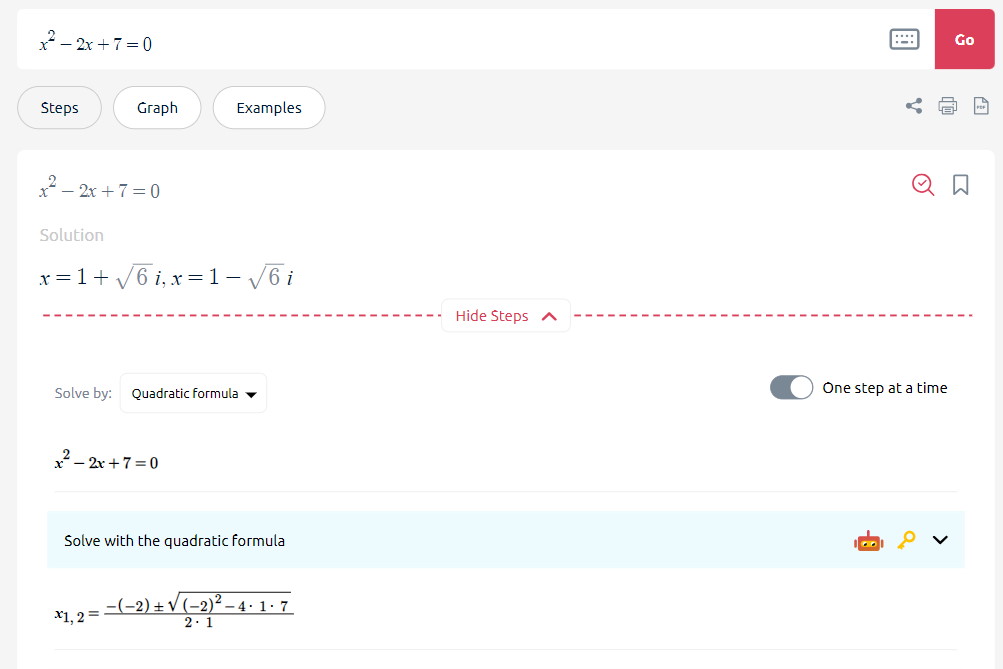
همان‌طور که مشاهده می‌کنید، جواب معادله $$ x ^ ۲ - ۲ x + ۷ = ۰ $$ به صورت اعداد مختلط به دست آمد. در نتیجه، محدودیتی در قابلیت‌های حل معادلات درجه دو توسط ابزارهای آنلاین و هوش مصنوعی وجود ندارد.

حل معادله درجه دو به روش دلتا پریم

روش دلتا پریم، یکی از روش‌های حل معادله درجه دو است که شباهت زیادی به روش دلتا دارد. در این روش، به جای ثابت $$ b $$ و پارامتر $$ \Delta $$، از پارامترهای $$ b ' $$ و $$ \Delta ' $$ (دلتا پریم) استفاده می‌شود. البته در روش دلتا پریم، $$ b $$ باید یک عدد زوج باشد.

برای آشنایی با فرمول‌های این روش، فرم کلی معادله درجه دو را در نظر بگیرید:

$$ a x ^ ۲ + b x + c = ۰ $$

فرمول حل این معادله به روش دلتا عبارت است از:

$$
x = \frac { - b \pm \sqrt { b ^ ۲ - ۴ a c } }{ ۲ a }
$$

$$ \Delta = b ^ ۲ - ۴ a c $$

در روش دلتا پریم، به جای $$ b $$ و $$ \Delta $$، پارامترهای زیر را تعیین می‌کنیم:

$$
b ^ { ' } = \frac { b } { ۲ }
$$

$$
\Delta ^ { ' } = b ^ { ' ۲ } - a c
$$

به این ترتیب، فرمول محاسبه ریشه‌های معادله درجه دو به روش دلتا پریم عبارت است از:

$$
x = \frac { - b ' \pm \sqrt { \Delta ' } }{ a }
$$

مثال ۵: ریشه گیری از معادله درجه ۲ به روش دلتا پریم

در این مثال، قصد داریم ریشه‌های معادله درجه دو $$ ۳ x ^ ۲ - ۶ x + ۲ = ۰ $$ را به روش دلتا پریم محاسبه کنیم. از آنجایی که $$ b = ۶ $$، یک عدد زوج است، برای حل این معادله می‌توانیم از روش دلتا پریم استفاده کنیم. به این منظور، ابتدا پارامترهای $$ b ' $$ و $$ \Delta ' $$ را به دست می‌آوریم:

$$ a = ۳ $$

$$ b = - ۶ $$

$$ c = ۲ $$

$$
\Delta ^ { ' } = b ^ { ' ۲ } - a c
$$

$$
\Delta ^ { ' } = b ^ { ' ۲ } - a c
$$

$$
\Delta ^ { ' } = ( - ۳ ) ^ { ۲ } - (۳ \times ۲ ) = ۹ - ۶ = ۳
$$

در نتیجه:

$$
x = \frac { - b ' \pm \sqrt { \Delta ' } }{ a }
$$

$$
x = \frac { - ( - ۳ ) \pm \sqrt { ۳ } }{ ۳ }
$$

$$
x _ ۱ = \frac {۳ + \sqrt { ۳ } }{ ۳ }
$$

$$
x _ ۲ = \frac {۳ - \sqrt { ۳ } }{ ۳ }
$$

حل تمرین حل معادله درجه دو به روش دلتا

در بخش‌های قبلی، به ارائه توضیحات ابتدایی در زمینه حل معادله درجه دو به روش دلتا و حل چندین مثال دستی و آنلاین پرداختیم. در این بخش، برای آشنایی بیشتر و بهتر با این موضوع، چند تمرین متنوع را حل می‌کنیم.

تمرین ۱

معادله درجه دو $$ ۳ x ^ ۲ + ۸ x - ۴ = ۰ $$ چند جواب حقیقی دارد؟

برای تعیین تعداد جواب‌های حقیقی یک معادله درجه دو، کافی است مقدار دلتای آن را به دست بیاوریم. به این منظور، از فرمول زیر استفاده می‌کنیم:

$$ \Delta = b ^ ۲ - ۴ a c $$

با توجه به ضرایب معادله مورد سوال، داریم؛

$$ a = ۳ $$

$$ b = ۸ $$

$$ c = - ۴ $$

این مقادیر را درون فرمول دلتا قرار می‌دهیم:

$$ \Delta = ۸ ^ ۲ - ۴ ( ۳ ) ( - ۴ ) $$

$$ \Delta = ۶۴ - ۴۸ $$

$$ \Delta = ۱۱۲ $$

دلتا، یک عدد مثبت است. بنابراین، معادله $$ ۳ x ^ ۲ + ۸ x - ۴ = ۰ $$، دارای دو جواب حقیقی خواهد بود.

تمرین ۲

تعداد جواب‌های حقیقی معادله درجه دو $$ ۵ x ^ ۲ + ۳ x + ۱ = ۰ $$ را مشخص کنید.

تعداد جواب‌های حقیقی یک معادله درجه ۲، با تعیین علامت دلتای آن معادله انجام می‌شود. فرمول محاسبه دلتای معادله درجه دو عبارت است از:

$$ \Delta = b ^ ۲ - ۴ a c $$

با توجه به ضرایب معادله مورد سوال، پارامترهای مورد نیاز برای محاسبه دلتا را می‌نویسیم:

$$ a = ۵ $$

$$ b = ۳ $$

$$ c = ۱ $$

این مقادیر را درون فرمول دلتا قرار می‌دهیم:

$$ \Delta = ۳ ^ ۲ - ۴ ( ۵ ) ( ۱ ) $$

$$ \Delta = ۹ - ۲۰ $$

$$ \Delta = -۱۱ $$

دلتا، یک عدد با علامت منفی است. به همین دلیل، معادله $$ ۵ x ^ ۲ + ۳ x + ۱ = ۰ $$، هیچ جواب حقیقی ندارد. البته جواب‌های این معادله، دو عدد مختلط خواهند بود.

تمرین ۳

معادله $$ ۶ x ^ ۲ + ۵ x - ۱ = ۰ $$ را حل کنید.

برای حل معادله درجه دو مورد سوال، از روش دلتا استفاده می‌کنیم. فرمول این روش به صورت زیر نوشته می‌شود:

$$
x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a }
$$

$$
x = \frac { - b \pm \sqrt { b ^ ۲ - ۴ a c } }{ ۲ a }
$$

بر اساس ضرایب معادله $$ ۲ x ^ ۲ + ۵ x - ۳ = ۰ $$، داریم:

$$ a = ۶ $$

$$ b = ۵ $$

$$ c = - ۱ $$

به این ترتیب، دلتا برابر است با:

$$ \Delta = ۵ ^ ۲ - ۴ ( ۶ ) ( - ۱ ) $$

$$ \Delta = ۲۵ + ۲۴ = ۴۹ $$

دلتا را به همراه دیگر مقادیر معلوم، درون فرمول محاسبه ریشه‌های معادله درجه ۲ قرار می‌دهیم:

$$
x = \frac { - ۵ \pm \sqrt { ۴۹ } }{ ۲ \times ۶ }
$$

$$
x = \frac { - ۵ \pm ۷ }{ ۱۲ }
$$

$$
x _ ۱ = \frac { - ۵ + ۷ }{ ۱۲ } = \frac { ۲ }{ ۱۲ } = \frac { ۱ }{ ۶ }
$$

$$
x _ ۲ = \frac { - ۵ - ۷ }{ ۱۲ } = \frac { -۱۲ }{ ۱۲ } = - ۱
$$

تمرین ۴

ریشه‌های معادله $$ x ^ ۲- ۶ x + ۹ = ۰ $$ را به دست بیاورید.

برای تعیین ریشه‌های معادله مورد سوال، از فرمول‌های روش دلتا استفاده می‌کنیم. این فرمول‌ها به صورت زیر نوشته می‌شوند:

$$
x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a }
$$

$$
\Delta ^ { ' } = b ^ { ' ۲ } - a c
$$

مقادیر زیر را برای استفاده در فرمول‌های بالا داریم:

$$ a = ۱ $$

$$ b = - ۶ $$

$$ c = ۹ $$

این مقادیر را در فرمول‌های حل معادله درجه دو جایگذاری می‌کنیم:

$$
\Delta = ( - ۶ ) ^ { ۲ } - ۴ ( ۱ ) ( ۹ ) = ۳۶ - ۳۶
$$

$$
\Delta = ۰
$$

مقدار دلتا برابر با صفر شد. بنابراین، با قطعیت می‌توانیم بگوییم که معادله مورد سوال، فقط یک ریشه (ریشه مضاعف) دارد که از رابطه زیر به دست می‌آید:

$$
x = \frac { - ( - ۶ ) }{ ۲ \times ۱ }
$$

$$
x = \frac { ۶ }{ ۲ }
$$

$$
x = ۳
$$

ریشه مضاعف معادله $$ x ^ ۲- ۶ x + ۹ = ۰ $$ برابر با $$ ۳ $$ است.

تمرین ۵

ریشه‌های معادله $$ ۵ x ^ ۲ - ۲ x = ۰ $$ چه هستند؟

برای به دست آوردن ریشه‌های یک معادله مورد سوال، از فرمول‌های زیر استفاده می‌کنیم:

$$
x = \frac { - b \pm \sqrt { \Delta } }{ ۲ a }
$$

$$ \Delta = b ^ ۲ - ۴ a c $$

پارامترهای موجود در این فرمول‌ها، ضرایب معادله درجه دو هستند. برای این تمرین، داریم:

$$ a = ۵ $$

$$ b = -۲ $$

$$ c = ۰ $$

بر اساس این مقادیر، مقدار دلتا برابر خواهد بود با:

$$ \Delta = ( - ۲ ) ^ ۲ - ۴ ( ۵ ) ( ۰ ) $$

$$ \Delta = ۴ - ۰ $$

$$ \Delta = ۴ $$

مقدار دلتا و دیگر پارامترهای معلوم را درون فرمول محاسبه ریشه‌های معادله درجه دو قرار می‌دهیم:

$$ x = \frac { - ( - ۲ ) \pm \sqrt { ۴ } }{ ۲ ( ۵ ) } $$

$$ x = \frac { ۲ \pm ۲ }{ ۱۰ } $$

$$ x _ ۱ = \frac { ۲ + ۲ }{ ۱۰ } = \frac { ۴ }{ ۱۰ } = \frac { ۲ }{ ۵ } $$

$$
x _ ۱ = \frac { ۲ - ۲ }{ ۱۰ } = \frac { ۰ }{ ۱۰ } = ۰
$$

تمرین ۶

معادله $$ - ۶ x ^ ۲ + ۴ x - ۱ = ۰ $$ را به روش دلتا پریم حل کنید.

برای حل یک معادله درجه دو به روش دلتا پریم، ابتدا زوج بودن ضریب $$ b $$ (ضریب متغیر $$ x $$) را بررسی می‌کنیم. در این تمرین، $$ b $$ برابر با یک عدد زوج است. بنابراین می‌توانیم روابط حل معادله درجه ۲ به روش دلتا پریم را بنویسیم. این روابط عبارت هستند از:

$$
b ^ { ' } = \frac { b } { ۲ }
$$

$$
\Delta ^ { ' } = b ^ { ' ۲ } - a c
$$

$$
x = \frac { - b ' \pm \sqrt { \Delta ' } }{ a }
$$

بر اساس ضرایب ثابت معادله، داریم:

$$ a = - ۶ $$

$$ b = ۴ $$

$$ c = - ۱ $$

با قرار دادن این مقادیر در روابط نوشته شده، خواهیم داشت:

$$
b ^ { ' } = \frac { ۴ } { ۲ } = ۲
$$

$$
\Delta ^ { ' } = ۲ ^ { ۲ } - ( - ۶ ) ( - ۱ ) = ۴ - ۶ = - ۲
$$

$$
x = \frac { - ۲ \pm \sqrt { -۲ } }{ - ۶ }
$$

همان‌طور که مشاهده می‌کنید، دلتا پریم (عبارت زیر رادیکال)، منفی شده است. بنابراین، این معادله، ریشه‌های حقیقی ندارد. البته امکان محاسبه ریشه‌های مختلط معادله وجود خواهد داشت. برای این کار، ابتدا رادیکال منفی را به صورت زیر بازنویسی می‌کنیم:

$$
\sqrt { -۲ } = \sqrt {- ۱} \sqrt { ۲ } = i\sqrt { ۲ }
$$

این عدد موهومی را درون فرمول ریشه‌های معادله قرار می‌دهیم:

$$
x = \frac { - ۲ \pm i \sqrt { ۲ } }{ - ۶ }
$$

$$
x _ ۱ = \frac { ۱ }{ ۳ } - i \frac { \sqrt { ۲ } }{ ۶ }
$$

$$
x _ ۲ = \frac { ۱ }{ ۳ } + i \frac { \sqrt { ۲ } }{ ۶ }
$$

به این ترتیب، ریشه‌های مختلط معادله مورد سوال را به دست آوردیم. حل معادله دو، روش‌های مختلفی دارد. روش دلتا، یکی از متداول‌ترین روش‌ها برای انجام این کار است. شاید در نگاه اول، استفاده از این فرمول کمی پیچیده به نظر بیاید. با این وجود، با حل مثال و تمرین‌های مختلف، می‌توان بر روی آن تسلط پیدا کرد.

سوالات متداول در رابطه با حل معادله درجه دو به روش دلتا

در بخش آخر این مطلب از مجله فرادرس، به برخی از پرتکرارترین سوالات مرتبط با مبحث حل معادله درجه دو به روش دلتا به صورت مختصر پاسخ می‌دهیم.

روش دلتا در حل معادله درجه دو چیست؟

روش دلتا، روشی است که ریشه‌های معادله درجه دو را با استفاده از یک فرمول مخصوص به دست می‌آورد.

کاربرد دلتا در حل معادله درجه دو چیست؟

دلتا، پارامتری است که امکان تعیین تعداد (یک یا دو) و نوع (حقیقی یا مختلط بودن) ریشه‌های معادله درجه دو را فراهم می‌کند.

ریشه مضاعف در حل معادله درجه دو چیست؟

اگر معادله درجه دو، فقط یک ریشه داشته باشد، می‌گوییم معادله دارای ریشه مضاعف است.

چه زمانی ریشه معادله درجه دو مضاعف می شود؟

زمانی که معادله درجه دو، محور افقی دستگاه مختصات را فقط در یک نقطه قطع کند، ریشه مضاعف به وجود می‌آید.

از کجا بفهمیم معادله درجه دو چند جواب دارد؟

با محاسبه دلتا و تعیین علامت آن، تعداد جواب‌های معادله درجه دو مشخص می‌شود. مثبت بودن دلتا، نشان‌دهنده وجود دو جواب حقیقی است. صفر شدن دلتا، وجود جواب مضاعف (یک ریشه حقیقی) را نمایش می‌دهد. در صورت منفی بودن دلتا، معادله درجه دو، هیچ ریشه حقیقی نخواهد داشت.

آیا ریشه های معادله درجه دو همیشه حقیقی هستند؟

خیر. اگر دلتای معادله درجه دو برابر با یک عدد منفی شود، ریشه‌های معادله، دو عدد مختلط خواهند بود.

روش دلتا پریم در حل معادله درجه دو چیست؟

روش دلتا پریم، روشی مشابه روش دلتا است که برای حل سریع‌تر معادله‌های درجه دو مورد استفاده قرار می‌گیرد. شرط استفاده از این روش، زوج بودن ضریب ایکس در معادله است.