تانژانت و کتانژانت – نسبت‌های مثلثاتی به زبان ساده

در مطلب دیگر مجله فرادرس با عنوان دایره مثلثاتی — به زبان ساده و سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده با نسبت‌های مثلثاتی آشنا شده‌اید. از آنجایی که این نسبت‌ها از هندسه وارد ریاضیات شده‌اند، در این نوشتار سعی می‌کنیم که ارتباط بین این نسبت‌ها، بخصوص تانژانت و کتانژانت را از نگاه هندسی بررسی کنیم. نسبت‌های مثلثاتی نقش مهمی در ریاضیات پایه و فیزیک و رشته‌های دیگر مهندسی دارند بنابراین آشنایی بیشتر با آن‌ها، درک مفاهیم در فیزیک و رشته‌های مهندسی را ساده‌تر می‌کند. پیش از هر چیز یادآور می‌شویم که سینوس را با نماد sin، کسینوس را با cos، تانژانت را با tan و کتانژانت را با cot نشان می‌دهیم.

تانژانت و کتانژانت روی محورهای دایره مثلثاتی

همه چیز از دایره مثلثاتی شروع شده است. دایره‌ای که شعاع آن برابر با واحد است. ممکن است شعاع این دایره یک متر، ۱ سانتی‌متر و حتی ۱۵ میلیمتر باشد ولی در این حالت نیز ۱۵ میلیمتر را به عنوان واحد اندازه‌گیری طول در نظر می‌گیریم. مرکز این دایره مثلثاتی روی نقطه مرکز مختصات دکارتی قرار گرفته است. پس مختصات این نقطه (0,0) است.

محور افقی در این مختصات محور کسینوس‌ها (Cos) و محور عمودی نیز سینوس (Sin) نامیده می‌شود. در تصویر زیر یک نمونه از دایره مثلثاتی دیده می‌شود. زاویه $$\theta$$ نیز در دایره مثلثاتی مشخص شده.

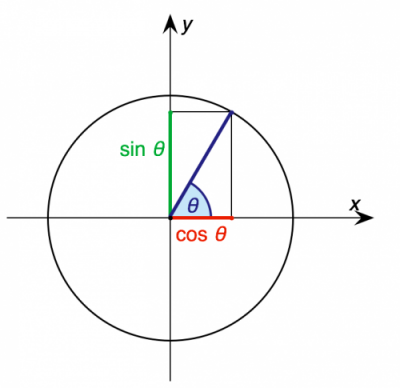
می‌دانیم که اگر خط مربوط به این زاویه را ادامه دهیم و از محل برخورد آن با دایره، خطی عمود به محور افقی ترسیم کنیم، می‌توانیم مقدار Cos را محاسبه کنیم. فاصله مرکز دایره تا محل برخورد خط عمود مقدار Cos زاویه $$\theta$$ را نشان می‌دهد. همچنین اگر از محل برخورد زاویه یا دایره، خطی عمود بر محور عمودی ترسیم کنیم، فاصله محل برخورد تا مرکز دایره نیز مقدار سینوس زاویه $$\theta$$ را نشان می‌دهد. این اندازه‌ها در تصویر بالا به خوبی نمایش داده شده‌اند.

محور تانژانت‌ها

حال به دستگاه مختصات یک محور دیگر اضافه می‌کنیم. از محل برخورد دایره با محور افقی، یک محور جدید موازی با محور عمودی ترسیم می‌کنیم. در نتیجه این محور عمود بر محور افقی است. در اینجا این محور را تانژانت می‌نامیم.

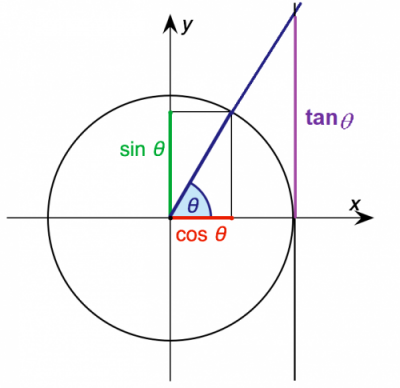
اگر خط مربوط به زاویه $$\theta$$ را ادامه دهیم تا این محور را قطع کند، طولی که روی این محور تا محور افقی ساخته می‌شود به نام تانژانت زوایه $$\theta$$ خوانده می‌شود. بنابراین برای هر زاویه به جز زاویه ۹۰ و ۹۰- درجه که تانژانت برایشان تعریف نشده، می‌توان تانژانت را از طریق اندازه‌گیری روی دایره مثلثاتی بدست آورد.

ولی از طرفی براساس روابط بین نسبت‌های مثلثاتی می‌دانیم که تانژانت هر زاویه برابر است با نسبت سینوس به کسینوس آن زاویه. به بیان ریاضی می‌توان نوشت:

$$\large \tan \theta =\dfrac{\sin \theta}{\cos \theta}$$

ولی با توجه به شکل چگونه می‌شود این رابطه را اثبات کرد؟ بهتر است از مهم‌ترین قضیه در هندسی که به قضیه تالس شهرت دارد کمک بگیریم. ابتدا صورت این قضیه را مرور می‌کنیم.

هرگاه چند خط موازی با استفاده از دو خط مورب، قطع شوند، نسبت‌های ایجاد شده روی آن‌ها با هم برابر‌ند.

بر این اساس خطوط ایجاد شده روی محورها و دایره مثلثاتی را نام‌گذاری می‌کنیم تا تصویر زیر حاصل شود. مشخص است که در اینجا خطوط BC و DE موازی بوده و خطوط AB, AC, AD و AE آن‌ها را قطع کرده‌اند.

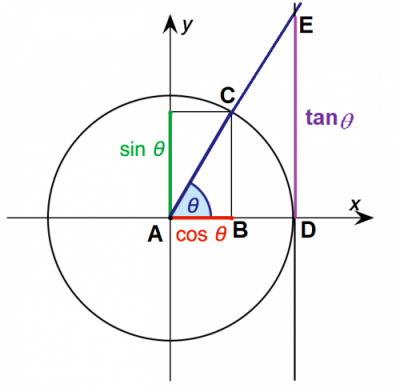
براساس قضیه تالس نسبت‌ خطوط مشابه ایجاد شده، با یکدیگر مساوی هستند. یعنی در این حالت می‌توان نوشت:

$$\large \dfrac{AC}{AE}=\dfrac{AB}{AD}$$

از آنجایی که AD و AC‌ هر دو شعاع دایره مثلثاتی هستند، طولشان برابر با ۱ است. در نتیجه رابطه بالا به شکل ساده‌تری در می‌آید و می‌توان بین AB و AE به رابطه زیر رسید:

$$\large \dfrac{1}{AE}=\dfrac{AB}{1} \rightarrow AE=\dfrac{1}{AB}$$

از طرفی طبق قضیه فیثاغورس در مثلث قائم‌الزاویه ADE (زاویه D قائمه است) که AE وتر است، داریم:

$$\large AE^2=AD^2+DE^2 \rightarrow AE^2-AD^2=AE^2-1=DE^2$$

نکته: به یاد دارید که AD شعاع دایره مثلثاتی است پس طول آن ۱ است.

حال اگر مقدار AE را با مقداری که در رابطه قبلی پیدا کردیم جایگزین کنیم به تساوی زیر خواهیم رسید:

$$\large \dfrac{1}{AB^2}-1=DE^2 \rightarrow \dfrac{1-AB^2}{AB^2}=DE^2$$

از طرفی می‌دانیم که در دایره ABC که قائم‌الزاویه نیز هست مربع طول ضلع BC برابر است با $$1-AB^2$$ پس رابطه بالا به شکل ساده‌تری در خواهد آمد.

$$\large \dfrac{‌BC^2}{AB^2}=DE^2 \rightarrow \dfrac{BC}{AB}=DE$$

نکته: از آنجایی که AC شعاع دایره است، طول آن برابر با ۱ است.

مشخص است که در آخر با استفاده از جذر تساوی را ساده‌تر کردیم. از آنجایی که همه طول‌ها مثبت هستند احتیاجی به استفاده از قدرمطلق یا علامت منفی هنگام جذرگیری نداریم. براساس دایره مثلثاتی می‌دانیم که DE همان $$\tan \theta$$ و $$BC$$ هم $$\sin \theta$$ و $$AB$$ نیز $$\cos \theta$$ است. بنابراین به کمک روش هندسی نشان دادیم که:

$$\large \tan \theta =\dfrac{\sin \theta}{\cos \theta}$$

به بیان دیگر می‌توان گفت که تانژانت یک زاویه در مثلث قائم‌الزاویه برابر با تقسیم «طول ضلع مقابل به زاویه» بر «طول ضلع مجاور به زاویه» است.

محور کتانژانت‌ها

می‌توان به مختصات دکارتی نیز یک محور جدید اضافه کرد تا روی آن مقدار کتانژانت زاویه اندازه‌گیری شود. این محور از محل برخورد دایره با محور عمودی و موازی محور افقی رسم می‌شود.

فیلم آموزش مثلثات– تناوب و تانژانت در حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک (رایگان) در فرادرس

کلیک کنید

در تصویر زیر محور کتانژانت در مختصات دکارتی و دایره مثلثاتی نمایش داده شده است. حال اگر زاویه $$\theta$$ را ادامه دهیم تا محور کتانژانت را قطع کند، طول حاصل از محل برخورد تا مرکز محور کتانژانت مقدار کتانژانت زاویه $$\theta$$ را نشان می‌دهد.

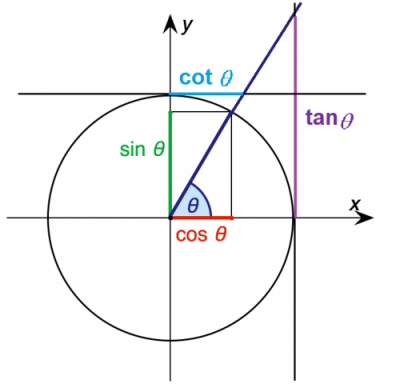
البته به همان ترتیبی که برای تانژانت ثابت کردیم می‌توان نشان داد کتانژانت هر زاویه برابر است با نسبت کسینوس به سینوس آن زاویه. به بیان ریاضی می‌نویسیم:

$$\large \cot \theta = \dfrac{\cos \theta}{\sin \theta}$$

در نتیجه رابطه بین تانژانت و کتانژانت زوایه $$\theta$$ به صورت زیر نوشته خواهد شد:

$$\large \cot \theta = \dfrac{1}{\tan \theta}$$

به بیان دیگر می‌توان گفت که کتانژانت یک زاویه در مثلث قائم‌الزاویه برابر با تقسیم «طول ضلع مجاور به زاویه» بر «طول ضلع مقابل به زاویه» است.

نکته: می‌دانیم که سینوس یک زاویه نیز برابر با تقسیم ضلع مقابل به وتر مثلث قائم‌الزاویه است. همچنین کسینوس نیز از تقسیم ضلع مجاور به زاویه بر وتر حاصل می‌شود.

جدول زیر به مقایسه مقدار سینوس، کسینوس، تانژانت و کتانژانت چند زاویه (از ۱۵ درجه تا ۹۰درجه) پرداخته است.

همانطور که دیده می‌شود، اگر زاویه $$\theta$$ برابر با 45 درجه یا همان $$\frac{\pi}{4}$$ باشد، مقدار تانژانت و کتانژانت برابر با ۱ هستند ولی در ۹۰ درجه یا $$\frac{\pi}{2}$$ تانژانت بی‌نهایت و کتانژانت صفر است. همینطور در صفر درجه نیز کتانژانت بی‌نهایت ولی تانژانت صفر است. در تصویر زیر، نمودار مربوط به تانژانت و کتانژانت با یکدیگر مقایسه شده‌اند.

تانژانت و کتانژانت مجموع دو زاویه

فرض کنید $$\alpha$$ و $$\beta$$ دو زاویه باشند. رابطه‌ای که برای محاسبه تانژانت و کتانژانت مجموع این دو زاویه وجود دارد به صورت زیر است:

$$\large \tan(\alpha+\beta)=\dfrac{\tan a\alpha+\tan \beta}{1-\tan \alpha \tan\beta}$$

$$\large \cot(\alpha+\beta)=\dfrac{\cot\alpha\cot\beta-1}{\cot \alpha +\cot\beta}$$

برای اثبات این رابطه‌ها بهتر است ابتدا رابطه سینوس و کسینوس جمع دو زاویه را یادآوری کنیم. برای دو زاویه $$\alpha$$ و $$\beta$$ می‌توان فرمول‌ زیر را برای سینوس اثبات کرد.

$$\large \sin (\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$$

همچنین رابطه‌ای برای کسینوس مجموع دو زاویه نیز وجود دارد:

$$\large \cos (\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta$$

با توجه به این رابطه‌ها، برای نشان دادن صحت رابطه اول برای تانژانت، کافی است مراحل زیر را طی کنیم.

$$\large \tan(\alpha+\beta)=\dfrac{\sin (\alpha+\beta)}{\cos (\alpha +\beta)}$$

براساس قاعده‌ای که برای سینوس و کسینوس جمع دو زاویه داریم، رابطه بالا را ساده می‌کنیم. در این حالت خواهیم داشت:

$$\large \tan (\alpha+\beta)= \dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta}$$

صورت و مخرج کسر را به $$\cos \alpha \cos \beta$$ تقسیم می‌کنیم.

$$\large \tan (\alpha+\beta)= \dfrac{\dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{{\cos \alpha \cos \beta}}}$$

به این ترتیب نتیجه حاصل خواهد شد.

$$\large \tan (\alpha+\beta)= \dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta}=\dfrac{\tan \alpha +\tan \beta}{1-\tan \alpha\tan\beta}$$

برای اثبات رابطه کتانژانت نیز کافی است رابطه مربوط به جمع کسینوس و سینوس دو زاویه را به $$\sin \alpha \sin \beta$$ تقسیم کنیم تا با کمی محاسبات نتیجه حاصل شود.