ارتعاشات آزاد با میراگر اصطکاکی – به زبان ساده

قبلاً در مجله فرادرس در مورد ارتعاشات آزاد در سیستم های نامیرا و ارتعاشات آزاد با میراگر ویسکوز، بحث و معادلات آن را ارائه کردیم. در این مقاله به بررسی ارتعاشات آزاد با میراگر اصطکاکی خواهیم پرداخت. در بسیاری از سیستم‌های مکانیکی، انواع میراگر اصطکاکی (Dry-Friction Damper) یا کلمب (Coulomb Damper) به دلیل سادگی، کاربرد فراوانی دارند. در سازه‌های ارتعاشی، هر زمان دو قسمت روی هم بلغزند، میرایی اصطکاکی درونی اتفاق افتاده است. بنا به قانون کلمب در حالت‌های اصطکاکی، هنگامی که دو جسم با هم در تماس هستند، نیروی مورد نیاز برای ایجاد لغزش، با نیروی قائم به صفحه تماس متناسب است. از این رو نیروی $$\large F$$ به صورت زیر خواهد بود.

$$\large F\:=\: \mu N\:=\: \mu W\:=\: \mu mg$$

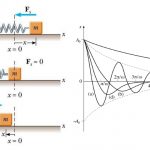
در رابطه بالا، $$\large N$$ نیروی قائم و برابر با وزن ($$\large W=mg$$)‌ است. ضریب $$\large \mu$$ نیز ضریب اصطکاک لغزشی یا جنبشی را نشان می‌دهد. بزرگی ضریب اصطکاک به جنس ماده‌های در حال تماس و وضعیت آن سطح بستگی دارد. مثلاً دو فلز مختلف را در نظر بگیرید که باهم در تماس باشند. در حالتی که سطوح تماس، روغن‌کاری شده باشد، ضریب اصطکاک برابر $$\large \mu \cong0.1$$ و در صورتی که روغن‌کاری انجام نشده باشد، ضریب اصطکاک برابر $$\large \mu \cong0.3$$ است. همچنین اگر تماس بین لاستیک و فلز انجام شود، مقدار این ضریب تقریباً به عدد یک خواهد رسید. نیروی اصطکاک در خلاف جهت حرکت وارد می‌شود. میراگر اصطکاکی تحت عنوان میراگر ثابت (Constant Damper) نیز شناخته می‌شود. زیرا این نیرو، به جابجایی و سرعت وابسته نبوده و فقط تحت تأثیر نیروی قائم $$\large N$$ است که بین سطوح تماس وارد می‌شود.

معادله حرکت در ارتعاشات آزاد با میراگر اصطکاکی

سیستم یک درجه آزادی با میراگر اصطکاکی را مطابق شکل زیر در نظر بگیرید. از آنجایی که نیروی اصطکاک با جهت سرعت تغییر می‌کند، دو حالت زیر را در نظر می‌گیریم.

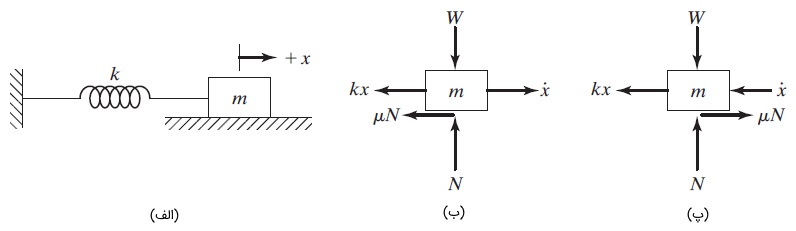
حالت اول: هنگامی که $$\large x$$، مثبت یا منفی و $$\large \frac {\text {d} x}{ \text {d}t}$$ حتماً مثبت باشد. این حالت با نیمی از سیکل، متناظر است که جرم از چپ به راست حرکت می‌کند. معادله حرکت با میراگر اصطکاکی را می‌توانیم با کمک قانون دوم نیوتن به دست آوریم (شکل ب).

$$\large m\ddot {x} \:+\:k x\:=\:-\: \mu N$$

(رابطه ۱)

رابطه بالا، معادله دیفرانسیل مرتبه دوم غیرهمگن بوده و پاسخ این معادله به صورت زیر است.

$$\large x(t)\: =\:A_1 \cos \omega _nt\: +\:A_2 \sin \omega _nt\:-\:\frac {\mu N} {k}$$

(رابطه 2)

در اینجا، $$\large \omega_n\: =\:\sqrt {k/m}$$ فرکانس ارتعاش است و ثابت‌های $$\large A_1$$ و $$\large A_2$$، براساس شرایط اولیه در این نیمه سیکل، به دست می‌آیند.

حالت دوم: در حالت دوم، $$\large x$$ مثبت یا منفی است و $$\large \frac {\text {d} x}{ \text {d}t}$$ مقداری منفی دارد. این حالت با نیمه دیگر سیکل متناظر است که در آن، جرم از راست به چپ حرکت می‌کند (شکل پ). معادله حرکت به صورت زیر نوشته می‌شود.

$$\large m\ddot {x}\:+\: kx\:=\: \mu N$$

(رابطه ۳)

پاسخ معادله دیفرانسیل بالا به صورت زیر است.

$$\large x(t)\: =\:A_3 \cos \omega _nt\: +\:A_4 \sin \omega _nt\:+\:\frac {\mu N} {k}$$

(رابطه 4)

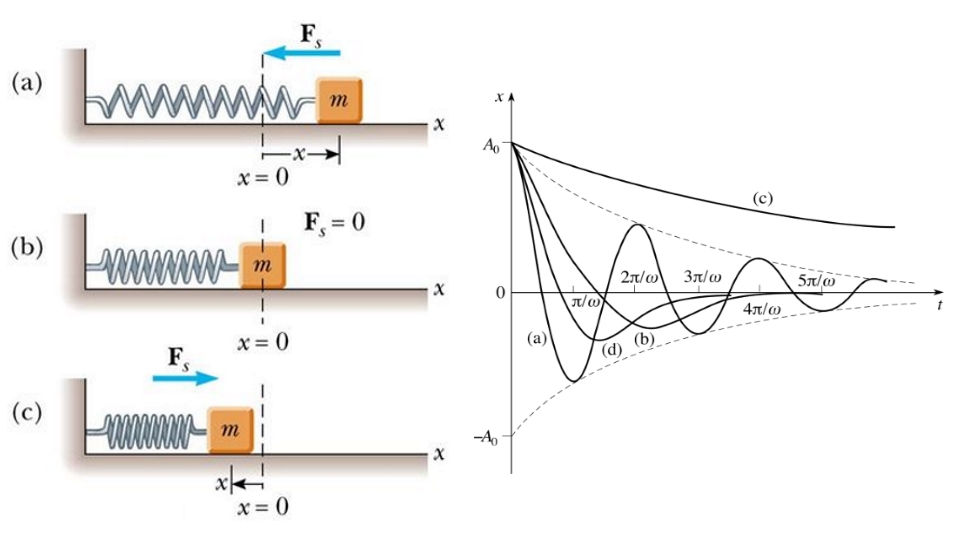
$$\large A_3$$ و $$\large A_4$$ ثابت‌های این معادله هستند که با توجه به شرایط اولیه به دست‌ می‌آیند. عبارت $$\large \frac {\mu N} {k}$$ که در هر دو رابطه ۲ و ۴ ظاهر شده است، مقدار ثابتی دارد و جابجایی مجازی فنر را تحت نیروی $$\large \mu N$$ و در شرایطی نشان می‌دهد که این نیرو به عنوان یک نیروی استاتیک وارد می‌شد. رابطه‌های ۲ و ۴ نشان می‌دهند که حرکت در هر کدام از نیمه‌های سیکل، هارمونیک است و موقعیت تعادل در هر نیمه، از $$\large \frac {\mu N} {k}$$ به $$\large -\:\frac {\mu N} {k}$$ تغییر می‌کند. این موضوع در شکل زیر نشان داده شده است.

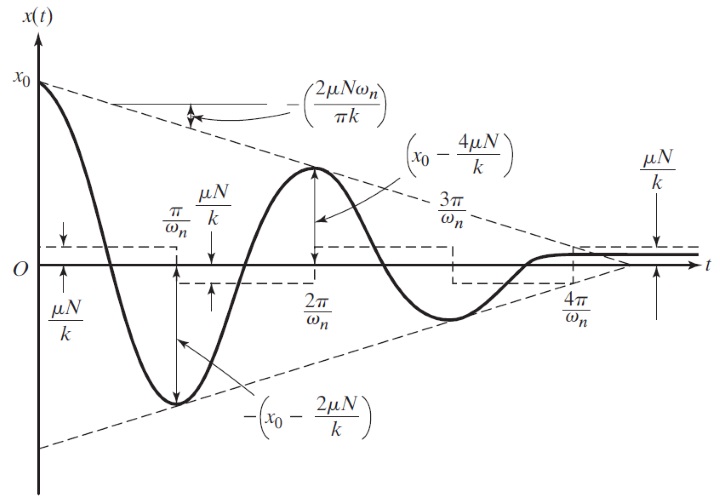
همچنین می‌توانیم رابطه‌های ۱ و ۳ را در قالب یک رابطه و به شیوه زیر بازنویسی کنیم.

$$\large m\ddot {x}\: +\:\mu mg\: \text {sgn}\: +\:kx \:=\:0$$

(رابطه ۵)

در رابطه اخیر، از تابع علامت استفاده کردیم که به صورت زیر تعریف می‌شود.

$$\large \text{sgn} (y)\:=\: \begin{cases}-1 & x < 0 \\ 0 & x = 0\\+1 & x > 0\end{cases}$$

رابطه شماره ۵، معادله دیفرانسیلی غیرخطی است که پاسخ تحلیلی ساده‌ای نمی‌توان برای آن یافت و باید از روش‌های عددی بدین منظور استفاده کرد. اما اگر محور زمان به بازه‌هایی شکسته شود که با خط $$\large \dot{x}=0$$ جدا شده باشد، می‌توانیم محاسباتمان را پیش ببریم. در نقاط $$\large \dot{x}=0$$، جهت حرکت تغییر می‌کند. برای یافتن پاسخ، شرایط اولیه را به صورت زیر فرض می‌کنیم.

$$\large x(t\:= \:0)\: =\:x_0 \\~\\ \large \dot {x}(t\: =\:0) \:=\:0$$

به عبارت دیگر، سیستم در زمان $$\large t=0$$، از نقطه $$\large x_0$$ و با سرعت صفر شروع به حرکت می‌کند. می‌توان نتیجه گرفت که در شروع، حرکت از راست به چپ است. دامنه‌های حرکت در نیم‌سیکل‌های متوالی را با $$\large x_0$$، $$\large x_1$$، $$\large x_2$$ و ... نشان می‌دهیم. با کمک رابطه شماره ۴ و شرایط اولیه، ثابت‌های $$\large A_3$$ و $$\large A_4$$ محاسبه می‌شوند.

$$\large A_3\:=\: x_0\:-\: \frac {\mu N} {k} \\~\\ \large A_4 \:=\:0$$

به این ترتیب، رابطه ۴ را به صورت زیر می‌نویسیم.

$$\large x(t)\: =\:(x_0 \:-\: \frac {\mu N} {k}) \cos \omega_nt\:+\: \frac {\mu N} {k}$$

(رابطه ۶)

این پاسخ فقط برای نیمی از سیکل و بازه $$\large 0\leq t\leq \pi/ \omega_n$$ معتبر است. هنگامی که $$\large t=\pi/ \omega_n$$ باشد، جرم به دورترین موقعیت خود در سمت چپ می‌رسد و جابجایی آن به شکل زیر نوشته می‌شود.

$$\large -\:x_1\:= \:x(t\: =\:\frac {\pi} {\omega _n})\:= \:(x_0\:-\: \frac {\mu N} {k}) \cos \pi\:+\:\frac {\mu N} {k}\:= \:-\:(x_ 0\:-\:\frac {2\mu N} {k})$$

از آنجایی که حرکت از نقطه $$\large x=x_0$$ آغاز شد و پس از نیمی از سیکل، مقدارش به $$\large -[x_0 - (2\mu N/k)]$$ رسیده است، کاهش مقدار $$\large x$$ در بازه زمانی $$\large \pi/ \omega_n$$ برابر $$\large 2\mu N/k$$ است. در نیمه دوم سیکل، جهت حرکت از چپ به راست است و باید از رابطه ۲ استفاده کرد. اکنون، شرایط اولیه را برای این نیمه از سیکل به دست می‌آوریم. برای محاسبه $$\large x(t\:=\:0)$$ و $$\large \dot{x}(t\:=\:0)$$، باید به ترتیب مقدار $$\large x$$ و $$\large \dot{x}$$ را در لحظه $$\large t=\pi/ \omega_n$$ و با کمک رابطه ۶ مشخص کنیم.

$$\large x(t\: =\:0)\:=\:-\: (x_0 \:-\:\frac {2\mu N} {k}) \\~\\ \large \dot{x}\:=\:-\:\omega_n(x_0\:-\:\frac{\mu n} {k} \sin \omega _nt) \\~\\ \large \Rightarrow ~~~\dot{x}(t\: =\:0)\:=\:0$$

به این ترتیب حالا می‌توانیم ثابت‌های رابطه ۲ را تعیین کنیم.

$$\large A_1\:=\: x_0\:-\: \frac{3 \mu N} {k} \\~\\ \large A_2\:=\:0$$

بازنویسی رابطه ۲ با ثابت‌های به دست آمده به شکل زیر خواهد بود.

$$\large x(t)\:=\: (x_0\:-\: \frac {3\mu N} {k}) \cos \omega _nt\:-\: \frac {\mu N} {k}$$

(رابطه ۷)

رابطه بالا فقط برای نیمه دوم سیکل و بازه زمانی $$\large \pi/\omega_n\:\leq t\leq 2\pi/ \omega_n$$ معتبر است. در انتهای این بازه، برای محاسبه $$\large x(t\:= \:\frac {2\pi} {\omega_n})$$ و $$\large \dot{x}(t\:= \:\frac {2\pi} {\omega_n})$$، باید به ترتیب مقدار $$\large x$$ و $$\large \dot{x}$$ را در لحظه $$\large t=2\pi/ \omega_n$$ و با کمک رابطه ۶ مشخص کنیم.

$$\large x(t\:= \:\frac {2\pi} {\omega_n})\:=\: x_0\:-\: \frac {4\mu N} {k} \\~\\ \large \dot{x}(t\:= \:\frac {2\pi} {\omega_n})\:=\: 0$$

این مقادیر، شرایط اولیه حرکت در نیم‌سیکل سوم هستند و به این ترتیب، تا زمان توقف، حرکت ادامه‌دار خواهد بود. در موقعیتی که $$\large x_n\leq\mu N/k$$ باشد، نیروی فنر ($$\large kx$$) از نیروی اصطکاک $$\large \mu N$$ کمتر است و در نتیجه، در این نقطه، جرم متوقف می‌شود. از این رو، تعداد نیم‌سیکل‌هایی ($$\large r$$) که پیش از توقف سپری می‌شود، به صورت زیر قابل تعریف است.

$$\large x_0\:-\: r\frac {2\mu N} {k} \:\leq\: \frac {\mu N} {k} \\~\\ \large r\:\geq [\frac {x_0\:-\: \frac {\mu N} {k}} {\frac {2\mu N} {k}}]$$

برخی از مشخصه‌های یک سیستم با میراگر اصطکاکی را ادامه مرور می‌کنیم.

• معادله حرکت در ارتعشات آزاد با میراگر ویسکوز، خطی بود ولی در مورد ارتعاشات آزاد با میراگر اصطکاکی غیر خطی است.
• فرکانس طبیعی سیستم با اضافه شدن میراگر اصطکاکی بدون تغییر باقی می‌ماند؛ ولی در ارتعاشات با میرایی ویسکوز، فرکانس طبیعی کاهش می‌یابد.
• در هنگام استفاده از میراگر اصطکاکی، حرکت به صورت تناوبی است ولی در مورد میراگر لزجی، ممکن است سیستم نوسان نداشته باشد (مانند حالت فوق میرایی).
• سیستمی که با میراگر اصطکاکی در حال ارتعاش است، پس از سپری شدن مدت زمان کمی متوقف می‌شود ولی از نظر تئوری، می‌تواند با میراگر ویسکوز تا زمان بینهایت به نوسان ادامه دهد.
• در ارتعاشات آزاد با میراگر اصطکاکی دامنه به صورت خطی کاهش پیدا می‌کند ولی در میراگر ویسکوز، این نسبت به صورت نمایی است. در هر دو سیکل متوالی، دامنه حرکت به اندازه $$\large 4\mu N/k$$ کوچکتر می‌شود. بنابراین، رابطه بین هر دو سیکل متوالی و همچنین، شیب خط گذرنده از دو قله مجاور، به صورت زیر است.

$$\large X_m\:=\: X_{m-1}\:-\: \frac {4\mu N} {k}\\~\\ \large -\:( \frac {4\mu N} {k})/( \frac {2\pi} {\omega _n})\:=\:-\:(\frac {2\mu N \omega _n} {\pi k})$$

ارتعاشات آزاد پیچشی با میراگر اصطکاکی

اگر یک گشتاور ثابت اصطکاکی به یک سیستم پیچشی وارد شود، معادله نوسان زاویه‌ای سیستم، مشابه رابطه‌های ۱ و ۳ و به صورت یکی از عبارت‌های زیر خواهد بود.

$$\large J_0 \ddot{ \theta} \:+\: k_t \theta \:=\:-\:T \\~\\ \large J_0 \ddot{ \theta} \:+\: k_t \theta \:=\:T$$

در دو رابطه بالا، $$\large T$$ گشتاور میرایی ثابت را نشان می‌دهد و با $$\large \mu N$$ در ارتعاشات خطی متناظر است. پاسخ این معادلات نیز مانند حالت خطی به دست می‌آید و فرکانس ارتعاشات برابر با $$\large \omega_n\:=\:\sqrt{\frac{k_t} {J_0}}$$ است. دامنه حرکت در انتهای $$\large r$$ اُمین نیمه از سیکل به شیوه زیر به دست می‌آید.

$$\large \theta_r\:=\: \theta_0\:-\: r\frac {2T} {k_t}$$

جابجایی زاویه‌ای اولیه در لحظه $$\large t=0$$ با $$\large \theta_0$$ نشان داده شده است. این حرکت، زمانی متوقف می‌شود که رابطه زیر برقرار باشد.

$$\large r\:\geq\: (\frac {\theta _0\:-\: \frac {T} {k_t}} {\frac {2T} {k_t}})$$

مثال ۱: محاسبه ضریب اصطکاک از روی موقعیت جرم

سؤال: یک بلوک فلزی که روی سطح زبر قرار دارد، به یک فنر متصل شده است. جابجایی اولیه این بلوک نسبت به موقعیت تعادلش، برابر با $$\large 10\: cm$$ است. پس از سپری شدن پنج سیکل نوسان در مدت $$\large 2\:s$$، بلوک فلزی در موقعیت نهایی $$\large 1\: cm$$ قرار می‌گیرد. ضریب اصطکاک بین سطح و بلوک فلزی را بیابید.

پاسخ: از آنجایی که پنج سیکل در مدت $$\large 2\:s$$ انجام شده است، دوره نوسان برابر $$\large \tau= 2/5= 0.4s$$ بوده و در نتیجه، فرکانس نوسان به صورت زیر محاسبه می‌شود.

$$\large \omega_n\:=\: \sqrt{ \frac {k} {m}}\:=\: \frac {2\pi} {\tau _n}\:=\: \frac {2\pi} {0.4} \:=\:15.708\: rad/s$$

کاهش دامنه نوسان در هر سیکل، از رابطه زیر تبعیت می‌کند. از این رو، کاهش دامنه را برای پنج سیکل، به شیوه زیر محاسبه می‌کنیم.

$$\large \frac {4\mu N} {k} \:=\:\frac {4\mu mg} {k} \\~\\ \large 5(\frac {4\mu mg} {k})\:=\: 0.10 \:-\: 0.01 \:=\: 0.09\:m \\~\\ \large \mu\:=\: \frac {0.09\:k} {20\:mg} \:=\: \frac {0.09\: \omega _n^2} {20\:g} \:=\: \frac {0.09 (15.708)^2} {20 (9.81)} \:=\: 0.1132$$

مثال ۲: قرقره در معرض میراگر اصطکاکی

سؤال: یک شفت فولادی به طول $$\large 1\:m$$ و قطر $$\large 50\:mm$$ را در نظر بگیرید. یک طرف این شفت، ثابت شده و در انتهای دیگرش، قرقره‌ای با ممان اینرسی $$\large 25\:kg.m^2$$ قرار گرفته است. یک نوار ترمزی طوری دور تا دور قرقره بسته شده تا گشتاور اصطکاکی ثابتی به اندازه $$\large 400N.m$$ ایجاد کند. اگر قرقره به اندازه $$\large 6^\circ$$ جابجا و سپس رها شود، الف) تعداد سیکل‌هایی که قرقره نوسان می‌کند تا متوقف شود و ب) موقعیت قرقره در توقف نهایی را محاسبه کنید.

پاسخ: الف) تعداد نیم‌سیکل‌هایی که طول می‌کشد تا حرکت زاویه‌ای قرقره متوقف شود، از رابطه زیر به دست می‌آید.

$$\large r\:\geq\: (\frac {\theta _0\:-\: \frac {T} {k_t}} {\frac {2T} {k_t}})$$

جابجایی اولیه $$\large \theta_0$$ در رابطه بالا برابر $$\large 6^\circ= 0.10472\:rad$$ است. برای محاسبه ثابت فنر پیچشی شفت، به طریق زیر عمل می‌کنیم.

$$\large k_t\:=\: \frac {GJ} {l}\:=\: \frac {(8\times 10^{10}) [\frac {\pi} {32} (0.05)^4]} {1}\:=\: 49,087.5 \:Nm/ rad$$

اکنون می‌تونیم تعداد نیم‌سیکل‌ها را به دست آوریم.

$$\large r\:\geq\: \frac {0.10472\:-\: (\frac {400} {49,087.5})} {(\frac {800} {49,087.5})} \:=\:5.926$$

بنابراین، شش نیم‌سیکل و در واقع، سه سیکل طول می‌کشد تا حرکت متوقف شود.

ب) برای محاسبه جابجایی زاویه‌ای پس از سپری شدن شش نیم‌سیکل، از رابطه زیر استفاده می‌کنیم.

$$\large \theta \:=\: \theta_0 \:-\: r(\frac {2T} {k_t}) \\~\\ \large \theta \:=\: 0.10472 \:-\: 6(\frac {2 \times 400} {49,087.5}) \:=\: 0.006935 \:rad \:=\: 0.39734 ^\circ$$

در نتیجه، قرقره در موقعیت $$\large 0.39734 ^\circ$$ و در همان سمتی که جابجایی اولیه داشت، متوقف خواهد شد.

اگر به مباحث مرتبط در زمینه مکانیک و ارتعاشات علاقه‌مند هستید، آموزش‌های زیر به شما پیشنهاد می‌شوند:

• ژیروسکوپ – از صفر تا صد
• ارتعاشات آزاد در سیستم های نامیرا – از صفر تا صد
• ارتعاشات مکانیکی — بخش سوم: سیستم‌های دو درجه آزادی

^^