آمار توصیفی چیست؟ – هر آنچه باید بدانید

اگر مدت زمان زیادی را صرف تجزیه و تحلیل دیتاست‌ها کرده باشید، حتما می‌دانید که در نهایت به علم آمار نیاز پیدا می‌کنید. آمار زیرشاخه‌ای از علم ریاضیات است که شامل جمع‌آوری، طبقه‌بندی، تحلیل، تفسیر و ارائه حقایق و اطلاعات عددی می‌شود و بسیار مناسب مسائلی است که با جمعیت‌های بالا و یا معیارهای اندازه‌گیری پیچیده سر و کار دارند. با بهره‌گیری از علم آمار می‌توان تنها با در اختیار داشتن نمونه کوچکی از دیتاست، به اطلاعات و نتایج مهمی دست یافت. در این میان، آمار توصیفی به رویکردی اشاره دارد که ویژگی‌های یک دیتاست را خلاصه و مرتب می‌کند. در این مطلب از مجله فرادرس یاد می‌گیریم آمار توصیفی چیست، چه کاربردی دارد و از چه انواعی تشکیل شده است. بخشی از علم آمار و احتمال که نقش مهمی در توصیف صفات یک متغیر یا ارتباط میان دو متغیر ایفا می‌کند.

در این مطلب ابتدا یاد می‌گیریم آمار توصیفی چیست، چه کاربردی داشته و از چه انواعی تشکیل شده است. سپس به بررسی تفاوت میان داده‌های تک متغیر و دو متغیره می‌پردازیم. در انتها این مطلب از مجله فرادرس به نقش تکنیک‌های مصورسازی و نمونه‌های پرت در آمار توصیفی اشاره داشته و از تفاوت آمار استنباطی با آمار توصیفی می‌گوییم.

تعریف آمار توصیفی چیست؟

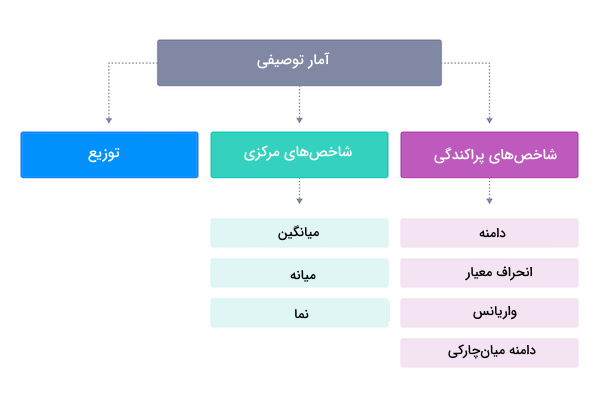
زیرشاخه‌ای از علم آمار که به خلاصه‌سازی، سامان‌دهی و ارائه معنادار داده‌ها می‌پردازد. تمرکز آمار توصیفی بر شرح و بررسی ویژگی‌های اصلی یک دیتاست بدون هیچ‌گونه تعمیم به جامعه آماری بزرگ‌تر است. به بیان ساده، هدف از آمار توصیفی را می‌توان در ارائه خلاصه‌ای قابل فهم از داده‌ها، فراهم کردن امکان تجزیه و تحلیل و درک الگوها و توزیع دیتاست تعریف کرد. چکیده یا خلاصه‌ای که متشکل از «شاخص‌های مرکزی» (Central Tendency) همچون میانگین، میانه و نما، «شاخص‌های پراکندگی» (Variability) مانند دامنه، واریانس و انحراف معیار و همچنین شکل توزیع از جمله «چولگی» (Skewness) و «کشیدگی» (Kurtosis) است.

فیلم آموزش آمار توصیفی با نرم افزار StatPlus (رایگان) در فرادرس

کلیک کنید

از طرف دیگر، در آمار توصیفی از شمایل گرافیکی مانند نمودار، گراف و جدول برای مصورسازی و تفسیر دقیق‌تر اطلاعات استفاده می‌شود. به عنوان برخی از تکنیک‌های گرافیکی رایج می‌توان به نمودار هیستوگرام، «میله‌ای» (Bar chart)، «دایره‌ای» (Pie chart)، «نقطه‌ای» (Scatter plot) و «جعبه‌ای» (Box plot) اشاره داشت. محققان با بهره‌گیری از آمار توصیفی می‌توانند علاوه بر درک بهتر داده‌ها، فرایند تصمیم‌گیری را تسهیل و میان اجزا کلیدی دیتاست ارتباط برقرار کنند. حالا که می‌دانیم منظور از آمار توصیفی چیست، در بخش بعد یاد می‌گیریم که اغلب در چه مواردی از آمار توصیفی استفاده می‌شود.

کاربرد آمار توصیفی

همان‌طور که پیش‌تر نیز توضیح دادیم، آمار توصیفی با ارائه خلاصه‌ای کوتاه از نمونه‌های داده، به شرح و بررسی موثر ویژگی‌های یک دیتاست کمک می‌کند. شناخته شده‌ترین انواع آمار توصیفی را شاخص‌های مرکزی تشکیل می‌دهند. برای مثال سه معیار میانگین، میانه و نما در اغلب سطوح ریاضی و آمار کاربرد داشته و در تعریف و همچنین توصیف مجموعه داده نقش دارند. برای محاسبه معیار میانگین ابتدا مجموع داده‌ها به‌دست آمده و سپس نتیجه بر تعداد کل نمونه‌های دیتاست تقسیم می‌شود. در دیتاستی با عناصر ۲، ۳، ۴، ۵ و ۶، مجموع ۲۰ و میانگین برابر با ۴ است.

فیلم آموزش آزمون های فرض میانگین جامعه در اس پی اس اس SPSS در فرادرس

کلیک کنید

از طرفی نما یا Mode به مقداری با بیشترین تکرار گفته می‌شود و میانه عنصری است که مقادیر دامنه بالا و پایین دیتاست را از هم جدا کرده و در میانه دیتاست قرار دارد. علاوه بر این موارد، شاخص‌های مهم دیگری نیز وجود دارند که کمتر شناخته شده هستند. عمده استفاده از آمار توصیفی در ساده‌سازی الگوهای پیچیده و کمی دیتاست خلاصه می‌شود. نقشی که به عنوان مثال معدل دانش‌آموزان در توصیف سطح علمی آن‌ها ایفا می‌کند. در حقیقت ایده معدل به این شرح است که از نمرات دروس مختلف میانگین گرفته شده و درک جامعی از عملکرد تحصیلی دانش‌آموزش به‌دست می‌آید.

چگونه مصورسازی داده را با فرادرس یاد بگیریم؟

همان‌طور که تا اینجا یاد گرفتیم، آمار توصیفی شاخه‌ای از علم آمار است که به توصیف و خلاصه‌سازی مجموعه داده‌ها می‌پردازد. این شاخه با استفاده از روش‌های مختلف مانند محاسبه میانگین، میانه، دامنه و انحراف معیار، ویژگی‌های اصلی داده‌ها را مشخص می‌کند. هدف اصلی آمار توصیفی، ارائه تصویری کلی و قابل فهم از دیتاست‌های پیچیده است. در این میان، مصورسازی داده‌ها نقش حیاتی در آمار توصیفی ایفا می‌کند. مصورسازی، فرایند تبدیل داده‌های خام به شمایل گرافیکی مانند نمودار و جدول است. این روش به ما امکان می‌دهد تا الگوها و ارتباطات پنهان میان داده‌ها را به سرعت شناسایی کنیم.

در همین جهت، پایتون به عنوان یکی از مهم‌ترین و پرکاربردترین ابزارها برای مصورسازی داده‌ها شناخته می‌شود. این زبان برنامه‌نویسی با کتابخانه‌های قدرتمندی مانند Seaborn و PyQtGraph، امکانات گسترده‌ای را برای ایجاد انواع نمودارها و گراف‌های پیشرفته فراهم می‌کند.

اگر علاقه‌مند به یادگیری مصورسازی داده‌ها هستید، مجموعه فیلم‌های آموزش مصورسازی فرادرس که لینک آن در بخش زیر قرار گرفته است، می‌تواند نقطه شروع بسیار خوبی باشد. این دوره‌ها با رویکردی عملی و کاربردی، شما را با اصول مصورسازی داده‌ها و نحوه استفاده از ابزارهای پایتون برای این منظور آشنا می‌کنند. از مفاهیم پایه تا تکنیک‌های پیشرفته، با کمک این مجموعه آموزشی می‌توانید مهارت‌های لازم را برای تبدیل داده‌های پیچیده به تصاویر گویا و جذاب کسب کنید:

• مجموعه فیلم‌های آموزش مصورسازی داده با پایتون فرادرس

انواع آمار توصیفی

تا اینجا یاد گرفتیم آمار توصیفی چیست و به چه منظور مورد استفاده قرار می‌گیرد. با این حال، همان‌طور که پیش‌تر نیز به آن اشاره شد، آمار توصیفی را می‌توان به سه دسته شاخص‌های پراکندگی، شاخص‌های مرکزی و توزیع تقسیم کرد. در ادامه این بخش، توضیحات بیشتری در مورد هر کدام از این شاخص‌ها ارائه می‌دهیم.

شاخص های پراکندگی

در این روش، میزان پراکندگی توزیع داده‌ها مورد سنجش و بررسی قرار می‌گیرد. به عنوان مثال، شاخص‌های مرکزی نمی‌توانند شکل توزیع داده‌ها را توصیف کنند. بنابراین اگر میانگین ۶۵ از ۱۰۰ باشد، همچنان امکان وجود نقاط داده با مقادیری همچون ۱ و ۱۰۰ وجود دارد. شاخص‌های پراکندگی با توصیف شکل و گستردگی دیتاست به رفع این مشکل کمک می‌کنند. دامنه، چارک، واریانس و انحراف مطلق، همه مثال‌هایی از شاخص‌های پراکندگی هستند.

دیتاستی با مقادیر ۵، ۱۹، ۲۴، ۶۲، ۹۱ و ۱۰۰ را در نظر بگیرید. دامنه این دیتاست برابر با حاصل تفاضل کوچک‌ترین عنصر یعنی ۵ از بزرگ‌ترین عنصر مجموعه داده یعنی ۱۰۰ است.

شاخص های مرکزی

تمرکز شاخص‌های مرکزی بر میانگین یا مقادیر مرکزی دیتاست است. به‌طور کلی شاخص‌های پراکندگی و مرکزی از نمودارها و جداول برای درک عمیق‌تر نتایج تجزیه و تحلیل‌های آماری استفاده می‌کنند. شاخص‌های مرکزی به شرح موقعیت مرکزی توزیع داده می‌پردازند. یک فرد متخصص میزان تکرار هر کدام از نمونه‌ها را در مجموعه داده تحلیل و با معیارهایی مانند میانگین، میانه یا مد توصیف می‌کند. به این صورت، رایج‌ترین الگوهای مجموعه داده اندازه‌گیری می‌شوند.

توزیع

منظور از توزیع یا توزیع فراوانی، تعداد دفعات تکرار یک نمونه است. از سوی دیگر، گاهی میزان عدم وقوع و تکرار یک نمونه نیز به عنوان توزیع آن در نظر گرفته می‌شود. دیتاستی را تصور کنید که شامل مقادیر مرد، مرد، زن، زن، زن و دیگر است. توزیع این دیتاست را می‌توان مانند زیر خلاصه کرد:

• تعداد مردها: ۲
• تعداد زن‌ها: ۳
• تعداد افرادی که جنسیت خود را مشخص نکرده‌اند: ۱
• تعداد غیر مردها: ۴

پس از آنکه یاد گرفتیم آمار توصیفی چیست و با انواع آن نیز آشنا شدیم، در ادامه این مطلب از مجله فرادرس به مقایسه دو مورد از رایج‌ترین نوع داده یعنی تک متغیره و دو متغیره می‌پردازیم. در مطلب دیگری از مجله فرادرس به‌طور ویژه و تخصصی درباره شاخص‌های آمار توصیفی توضیح داده‌ایم که از طریق لینک زیر قابل مطالعه است:

تک متغیره و دو متغیره

در آمار توصیفی،‌ از داده‌های تک متغیره برای شناسایی تک ویژگی‌ها استفاده می‌شود و کاربردی در تحلیل روابط میان نمونه‌ها ندارد. برای مثال، اتاقی پر از دانش‌آموزان دبیرستانی را تصور کنید. هدف شما گردآوری میانگین سن دانش‌آموزان است. معیاری که برای محاسبه تنها به یک متغیر یعنی سن نیاز دارد. اما هدف از داده‌های دو متغیره، یافتن همبستگی و برقراری ارتباط میان دو متغیر است. از این رویکرد با عنوان «چند متغیره» (Multivariate) نیز یاد می‌شود. برای آشنایی بیشتر با نحوه تحلیل کاربردی داده‌های چند متغیره، می‌توانید فیلم آموزش آنالیز داده‌های چند متغیره فرادرس را از لینک زیر مشاهده کنید:

فیلم آموزش آنالیز داده های چند متغیره با نرم افزار Unscrambler X در فرادرس

کلیک کنید

در ادامه مثال قبل، می‌خواهیم بر اساس نتایج امتحانی سراسری، عملکرد دانش‌آموزان بزرگ‌تر را -از نظر سن- نسبت به دانش‌آموزان جوان‌تر بسنجیم. با جمع‌آوری نمرات و همچنین سن دانش‌آموزان، می‌توان ارتباط میان این دو متغیر را تحلیل و همچنین ترسیم کرد. توجه داشته باشید که در تحلیل دو متغیره و به‌منظور کشف تفاوت‌ها، همزمان میزان تکرار و پراکندگی دو متغیر بررسی می‌شود.

مصورسازی در آمار توصیفی

تا اینجا به‌خوبی می‌دانیم آمار توصیفی چیست، شامل چه انواعی شده و با دو نوع از داده‌های تک متغیره و دو متغیر آشنا شدیم. علاوه بر این موارد، نمایش گرافیکی و مصورسازی نیز جنبه مهمی در آمار توصیفی داشته و به چند روش مختلف که در ادامه توضیح می‌دهیم قابل انجام است.

فیلم آموزش مصورسازی داده یا Data Visualization در نرم افزار R با بسته ggplot2 در فرادرس

کلیک کنید

نمودار نقطه ای

نموداری که ارتباط میان دو یا سه متغیر را نشان می‌دهد. در نمودار نقطه‌ای، یک متغیر بر محور افقی ($$x$$) و متغیر دیگر بر محور عمودی ($$y$$) تصویر می‌شود. همچنین ترسیم نمونه‌ها به شکل نقاطی پراکنده در نمودار است.

نمودار هیستوگرام

ابزاری برای نمایش توزیع داده‌های عددی است. در این نمودار برای هر نمونه و تعداد مرتبه‌ای که تکرار شده است دسته مجزایی در نظر گرفته می‌شود. با کمک نمودار هیستوگرام می‌توان شکل توزیع، شاخص‌های مرکزی و همچنین پراکندگی داده‌ها را به‌دست آورد.

نمودار جعبه ای

این نمودار با عنوان «جعبه و خط» (Box and Whisker) نیز شناخته می‌شود و با تاکید بر معیارهای آماری چون میانه (خط وسط جعبه)، چارک (گوشه‌های جعبه) و نمونه‌های پرت (نقاط بیرونی)، خلاصه دقیقی از توزیع داده‌ها ارائه می‌دهد. نمودار جعبه‌ای میزان پراکندگی داده‌ها را به تصویر کشیده و مناسب زمانی است که بخواهیم توزیع داده‌ها را بر اساس چند دسته یا متغیر با یک‌دیگر مقایسه کنیم.

آمار توصیفی و نمونه های پرت

بدون اشاره به نمونه‌های پرت نمی‌توان گفت آمار توصیفی چیست و چگونه کار می‌کند. نمونه‌های پرت به نقاط دور افتاده‌ای در دیتاست گفته می‌شود که بیانگر خطا، ناهنجاری یا رخدادهای نادر هستند. شناسایی و مدیریت این نمونه‌ها قدمی مهم در آمار توصیفی برای مطمئن شدن از دقت تجزیه و تحلیل است. برای این منظور، بهره‌گیری از تکنیک‌های گرافیکی مانند نمودار نقطه‌ای یا جعبه‌ای و همچنین روش‌های آماری مانند Z-score و «دامنه میان چارکی» (Interquartile Range | IQR) پیشنهاد می‌شود.

فیلم آموزش تشخیص داده های پرت یا Outlier Detection – رایگان در فرادرس

کلیک کنید

وجود داده‌های پرت تاثیر بسیاری بر نتایج، نحوه تفسیر داده‌ها و به‌طور کلی آمار توصیفی می‌گذارد. بنابراین ممکن است شاخص‌های مرکزی مانند میانگین تحت تاثیر قرار گرفته و به سمت «مقادیر حدی» (Extreme Values) میل کنند. به عنوان مثال میانگین دیتاستی با عناصر ۱، ۱، ۱ و ۹۹۷ برابر با ۲۵۰ است که نمی‌تواند معرف خوبی برای مجموعه داده باشد. چنین خطاهایی ممکن است به نتیجه‌گیری نادرست درباره وضعیت و توزیع دیتاست منجر شوند.

بسته به نوع محتوا، می‌توان داده‌های پرت نامرتبط و پرخطا را از دیتاست حذف کرد. اما شاید این قبیل از داده‌ها شامل اطلاعات ارزشمندی باشند که حذف آن‌ها را ناممکن می‌سازد. در نتیجه هنگام تجزیه و تحلیل اطلاعات، باید به میزان اهمیت و مشارکت داده‌های پرت در محاسبات آمار توصیفی توجه داشته باشید.

تفاوت آمار استنباطی و آمار توصیفی چیست؟

تفاوت آمار توصیفی با آمار استنباطی در دیتاست‌هایی است که از آن‌ها برای تصمیم‌گیری استفاده می‌شود. شرکتی را در نظر بگیرید که در زمینه فروش سس تند فعالیت دارد. این شرکت اطلاعاتی همچون تعداد فروش، میانگین تعداد خرید به‌ازای هر تراکنش و میانگین فروش در هر روز هفته را جمع‌آوری می‌کند. همه این اطلاعات توصیفی بوده و روایت‌گر داستانی از رویدادهای گذاشته هستند.

حالا همین شرکت قصد رونمایی از سس تند جدیدی را دارد. مجدد شروع به جمع‌آوری همان اطلاعات، اما این‌بار به هدف پیش‌بینی حجم فروش محصول می‌کند. در نتیجه، دیگر نیازی به خلاصه‌سازی داده‌ها نبوده و پیش‌بینی‌ها نسبت به محصول جدید و صرف‌نظر از نمونه‌های قبلی صورت می‌گیرند. رویکردی که با عنوان آمار استنباطی از آن یاد می‌شود. به بیان دیگر، در حالی که آمار توصیفی به خلاصه‌سازی ویژگی‌های دیتاست می‌پردازد، آمار استنباطی امکان آزمایش فرضیه‌ها یا قابلیت تعمیم داده را به جوامع آماری بزرگ‌تر مهیا می‌کند.

آمار استنباطی به ما اجازه می‌دهد تا با استفاده از داده‌های نمونه به نتایجی درباره‌ی کل توزیع برسیم و فرضیات آماری را مورد بررسی و آزمایش قرار دهیم. پلتفرم فرادرس فیلم‌های آموزشی جامعی را از مباحث تئوری تا کاربردی در زمینه آمار استنباطی و به‌ویژه علوم انسانی تهیه و تولید کرده است که مشاهده آن‌ها را از طریق لینک‌های زیر به شما پیشنهاد می‌کنیم:

• فیلم آموزش رایگان آمار استنباطی فرادرس
• فیلم آموزش آمار استنباطی برای مدیریت و علوم انسانی فرادرس
• فیلم آموزش رایگان کاربرد رگرسیون و همبستگی در آمار استنباطی برای مدیریت و علوم انسانی فرادرس

جمع‌بندی

تجزیه و تحلیل، خلاصه‌سازی و اشتراک‌گذاری صفات مجموعه داده از جمله کارکردهای آمار توصیفی است. در این مطلب از مجله فرادرس به این پرسش پاسخ دادیم که آمار توصیفی چیست، چه کاربردی داشته و با انواع مختلف آن آشنا شدیم. رویکردی که اگرچه برای تصمیم‌گیری و پیش‌بینی نهایی چندان مفید نبوده، اما کاربرد زیادی در استخراج اطلاعات سطح بالا همچون میانگین، واریانس و دامنه داشته و دید خوبی از توزیع و شکل کلی داده‌ها در اختیار ما قرار می‌دهد.