کار خازن چیست؟ — به زبان ساده

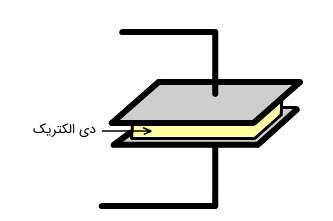
در این مطلب قصد داریم کار خازن را بررسی کنیم. یک خازن از دو صفحه فلزی تشکیل شده است که توسط ماده‌ای نارسانا یا دی‌ الکتریک جدا می‌شود. در این مطلب کار خازن را در دو حالت ولتاژ ثابت و بار الکتریکی ثابت بررسی کرده‌ایم.

خازن

اگرچه از هر ماده غیر رسانایی می‌توان به عنوان دی الکتریک استفاده کرد اما در عمل برخی مواد خاص مانند پرسلن، مایلار، تفلون، میکا، سلولز و غیره بدین منظور مورد استفاده قرار می‌گیرند. یک خازن با توجه به نوع دی الکتریک انتخاب شده تعریف می‌شود و همچنین نوع دی الکتریک در کاربرد خازن نیز موثر است.

فیلم آموزش فیزیک – پایه یازدهم در فرادرس

کلیک کنید

با توجه به اندازه و نوع دی الکتریک مورد استفاده از خازن می‌توان برای اهداف کاربردی با ولتاژ بالا و همچنین ولتاژ پایین استفاده کرد.

برای کاربردهای متفاوت مواد مختلف به عنوان دی الکتریک مورد استفاده قرار می‌گیرند. به عنوان مثال در مدارهای تنظیم رادیویی هوا، در مدارهای زمان‌سنج مایلار، برای کاربردهایی با ولتاژ بالا شیشه و برای استفاده در دستگاه‌های اشعه ایکس و MRI سرامیک بیشتر به عنوان دی الکتریک استفاده می‌شوند.

صفحات فلزی خازن با فاصله $$d$$ از هم جدا می‌شوند و یک ماده دی الکتریک در بین این صفحات قرار می‌گیرد.

دی الکتریک ماده اصلی در خازن است که به ذخیره انرژی الکتریکی کمک می‌کند. ثابت دی الکتریک مواد مختلف برابر با $$K\epsilon_{0}$$ است که $$\epsilon_{0}$$ ثابت دی الکتریک هوا است.

کاربرد خازن

متداول‌ترین کاربرد برای خازن‌ها ذخیره انرژی است. موارد دیگر شامل استفاده در دستگاه‌های تهویه الکتریکی، اتصال یا قطع سیگنال‌های الکتریکی، فیلترهای صوتی الکترونیکی و سنجش از راه دور است. به دلیل کاربردهای متنوع، خازن‌ها در طیف وسیعی از صنایع مورد استفاده قرار می‌گیرند و به بخشی حیاتی از زندگی روزمره تبدیل شده‌اند.

کاربرد خازن‌ها در ذخیره انرژی

از اواخر قرن هجدهم از خازن‌ها برای ذخیره انرژی الکتریکی استفاده می‌شود. بنجامین فرانکلین اولین کسی بود که عبارت باتری را برای تعدادی از خازن‌ها در یک دستگاه ذخیره انرژی به کار برد. خازن‌های منفرد به طور کلی انرژی زیادی را ذخیره نمی‌کنند و فقط نیروی کافی برای استفاده از دستگاه‌های الکترونیکی در هنگام قطع موقتی برق یا در صورت نیاز دستگاه‌های الکترونیکی به برق اضافی را تأمین می‌کنند. به عنوان مثال خازن‌های بزرگی در سیستم‌های صوتی اتومبیل گنجانده شده‌اند تا در صورت لزوم صدای بیشتری تولید کنند.

کاربرد خازن‌ها در دستگاه‌های تهویه مطبوع

یکی از کاربردهای مهم خازن‌ها در منبع تغذیه دستگاه‌های تهویه مطبوع است. در این دستگاه‌ها در هنگام شارژ شدن خازن‌ها اجازه عبور سیگنال‌های AC را می‌دهند اما سیگنال‌های DC را مسدود می‌کنند.

این خازن‌ها می‌توانند به طور موثر این دو نوع سیگنال را تقسیم کرده و منبع تغذیه را تمیز كنند. این اثر برای جدا کردن قسمت‌های مختلف مدارهای الکتریکی برای کاهش نویز مورد استفاده قرار می‌گیرد ولی این روش می‌تواند منجر به کاهش کارایی دستگاه شود.

کاربرد خازن‌ها به عنوان سنسور

خازن‌ها به عنوان سنسور برای اندازه‌گیری موارد مختلف از جمله رطوبت هوا، سطح سوخت و فشار مکانیکی استفاده می‌شوند. ظرفیت یک دستگاه به ساختار آن بستگی دارد. تغییرات در ساختار یک دستگاه را می‌توان به عنوان کاهش یا افزایش ظرفیت اندازه‌گیری کرد.

در سنسورها از دو ویژگی خازن می‌توان بهره جست فاصله بین صفحات خازن و ماده دی الکتریک بین آن‌ها.

از تغییر فاصله صفحات خازن برای تشخیص تغییرات مکانیکی مانند شتاب و فشار و استفاده می‌شود. همچنین تغییرات جزئی در مواد بین صفحات خازن می‌تواند منجر به تغییر ظرفیت خازن شود که از این ویژگی می‌توان برای سنجش رطوبت هوا استفاده کرد.

کاربرد خازن‌ها در پردازش سیگنال

کاربرد فزاینده خازن‌ها در فن‌آوری اطلاعات بر هیچ کس پوشیده نیست. دستگاه‌های حافظه پویا (DRAM) از خازن‌ها برای نمایش اطلاعات باینری به عنوان بیت استفاده می‌کنند. این دستگاه‌ها هنگام شارژ خازن یک مقدار و هنگام تخلیه مقدار دیگری را می‌خواند.

CCD یا دستگاه جفت کنندهٔ بار که یک حسگر تصویربرداری است و از یک مدار یکپارچه تشکیل شده که شامل آرایه‌ای از اتصالات یا خازن‌های حساس است، از خازن به صورت آنالوگ استفاده می‌کند.

همچنین از خازن‌ها به همراه سلف‌ها برای تنظیم مدار با فرکانس‌های خاص استفاده می‌شود. این اثر در گیرنده‌های رادیویی، بلندگوها و اکولایزرهای آنالوگ مشاهده می‌شود.

محاسبه کار خازن

خازن شبیه یک باتری است. اگرچه این دو به روش‌های کاملاً متفاوتی کار می‌کنند اما خازن‌ها و باتری‌ها هر دو انرژی الکتریکی را ذخیره می‌کنند. اگر با نحوه کار باتری‌ها آشنایی داشته باشید می‌دانید که یک باتری دو ترمینال دارد. در داخل باتری واکنش‌های شیمیایی باعث تولید الکترون در یک ترمینال و جذب الکترون در ترمینال دیگر می‌شوند. خازن بسیار ساده‌تر از باتری است زیرا نمی‌تواند الکترون‌های جدید جذب کند و فقط آن‌ها را ذخیره می‌کند.

در داخل خازن ترمینال‌ها به دو صفحه فلزی متصل می‌شوند که توسط یک ماده نارسانا یا دی الکتریک جدا شده‌اند. به راحتی می‌توانید از دو قطعه فویل آلومینیوم و یک کاغذ خازن درست کنید. این خازن از نظر ظرفیت ذخیره سازی خازن خوبی نخواهد بود اما کار می‌کند.

کاری که توسط خازن صفحه موازی انجام می‌شود در حالتی که فاصله بین صفحات تغییر ‌کند قابل محاسبه است. در این مطلب دو حالت در نظر گرفته شده است: 1) بار خازن ثابت باشد. 2) ولتاژ دو سر خازن ثابت باشد.

کار خالص زمانی محاسبه می‌شود که دستگاه در نمودار بار الکتریکی-ولتاژ یک مساحت بسته را طی کند. در این حالت مساحت زیر نمودار برابر با کار مکانیکی انجام شده توسط خازن است.

اگر به فکر انجام کار مکانیکی با باتری هستیم بلافاصله یک موتور الکتریکی به ذهن خطور می‌کند زیرا این روش معمول تبدیل انرژی الکتروشیمیایی ذخیره شده در باتری به کار مکانیکی است.

در این مطلب یک خازن صفحه موازی را در نظر می‌گیریم که فاصله بین صفحات آن با هوا پر شده باشد و کار خازن را در این حالت بررسی می کنیم. واضح است که اگر فاصله بین صفحات خازن با ماده دیگری غیر از هوا پر شده باشد در معادلات ارائه شده در این مطلب به جای $$\epsilon_{0}$$ از $$K \epsilon_{0}$$ استفاده خواهد شد که $$K$$ ثابت دی الکتریک ماده است. بدین ترتیب روش‌های به کار رفته در این مطلب قابل تعمیم به هر خازن دیگری است.

مساحت صفحات خازن $$A$$ است، شکاف بین آن‌ها پر از هوا و فاصله بین صفحات برابر با $$x$$ است. بنابراین نفوذ پذیری دی الکتریک برابر با $$\epsilon_{0}$$ است.

اولین حالتی که در این مطلب بررسی می‌کنیم کار انجام شده توسط یک خازن با بار ذخیره شده ثابت است که فاصله بین صفحات آن تغییر می‌کند.

در این حالت یک خازن را در نظر می‌گیریم که در ابتدا بدون بار است و فاصله بین صفحات آن $$x_{i}$$ است. یک باتری با ولتاژ $$v_{i}$$ به خازن متصل شده و آن را به اندازه $$q$$ باردار می‌کند. بعد از آن خازن از باتری جدا می‌شود اما همچنان بار آن ثابت است.

فضای بین صفحات خازن از $$x_{i}$$ به $$x_{f}$$ تغییر می‌کند و برای جبران تغییر فاصله بین صفحات، خازن کار انجام می‌دهد. هدف ما محاسبه کار $$W_{q}$$ است که اندیس $$q$$ به معنای وجود سیستم با بار ثابت است.

برای محاسبه کار خازن باید تغییرات در پتانسیل خازن را بررسی کرد.

از مطلب انرژی خازن می‌دانیم انرژی ذخیره شده در خازن برابر با $$U=\frac{q}{2C}$$ است که $$C$$ نشان‌دهنده ظرفیت خازن است. برای یک خازن صفحه موازی که فاصله بین صفحات آن با هوا پر شده است ظرفیت برابر با $$C=\frac{\epsilon_{0}A}{d}$$ است و می توان نوشت:

$$\large W_{q}=E_{f}-E_{i}$$
$$\large \Rightarrow \frac{1}{2}\frac{q^{2}}{C_{f}}-\frac{1}{2}\frac{q^{2}}{C_{i}}$$
$$\large \Rightarrow = \frac{1}{2}\frac{q^{2}}{\epsilon_{0}A}(x_{f}-x_{i})$$

فیلم آموزش فیزیک الکتریسیته + مفاهیم کلیدی در فرادرس

کلیک کنید

معادل بالا صریحاً نشان می‌دهد که بار ذخیره شده در روند انجام کار ثابت است. با این حال نوشتن معادله بالا بر حسب ولتاژ نیز مفید است همان طور که در مطالب مربوط به خازن گفته شد رابطه بین ظرفیت خزان، بار الکتریکی و ولتاژ به صورت $$C=\frac{q}{V}$$ است. در نتیجه کار خازن در یک خازن صفحه موازی در حالتی که فاصله بین صفحات خازن تغییر کند برابر است با:

$$\large W_{q} =\frac{\epsilon_{0}AV_i^2}{2x_i^2}(x_{f}-x_{i})$$

در معادله بالا از رابطه ظرفیت بر حسب سطح مقطع و فاصله بین صفحات استفاده کرده‌ایم. بدین ترتیب کار انجام شده توسط یک خازن صفحه موازی را پیدا کردیم که به یک باتری متصل شده است که ولتاژ آن $$V_{i}$$ است. بعد از مدتی خازن بار الکتریکی $$q$$ را به دست آورده و از باتری جدا می‌شود. در این حالت فاصله بین صفحات خازن از $$x_{i}$$ به $$x_{f}$$ تغییر می‌کنند در حالی که بار روی خازن ثابت است. یعنی داریم:

$$\large q=C_{i}V_{i}=C_{f}V_{f}$$

بدین ترتیب نسبت زیر بین ولتاژ و فاصله بین صفحات خازن برقرار است.

$$\large \frac{V_{i}}{x_{i}}=\frac{V_{f}}{x_{f}}$$

برای به دست آوردن این نسبت از رابطه ظرفیت بر حسب سطح مقطع و فاصله بین صفحات استفاده کردیم.

مرحله بعدی محاسبه کار انجام شده توسط خازن در هنگام ثابت بودن ولتاژ است. خازن به ولتاژ $$V$$ به یک باتری متصل می‌شود و فاصله بین صفحات خازن از $$x_{i}$$ به $$x_{f}$$ تغییر می‌کند. از طرفی می‌دانیم رابطه بین نیرو و انرژی به صورت زیر است و داریم:

$$\large F=-\frac{\partial E}{\partial x}$$
$$\large \rightarrow = -\frac{\partial}{\partial x}(\frac{1}{2}\frac{\epsilon_{0}AV^{2}}{x})$$
$$\large \rightarrow F=\frac{\epsilon_{0}AV^{2}}{2x^{2}}$$

کار لازم برای تغییر فاصله بین صفحات خازن موازی در ولتاژ ثابت به صورت زیر قابل محاسبه است:

$$\large W_{V}=\int_i^fF\ dx$$
$$\large \rightarrow =\int_i^f\frac{\epsilon_{0}AV^{2}}{2x^{2}}$$
$$\large \Rightarrow W_{V}=\frac{\epsilon_{0}AV^{2}}{2}(\frac{1}{x_{i}}-\frac{1}{x_{f}})$$

اندیس $$V$$ به این معنی است که فرایند در ولتاژ ثابت انجام شده است. باید گفت که روش آسانتر محاسبه کار در این حالت استفاده از رابطه کار و انرژی پتانسیل در خازن است. می‌دانیم که منفی تغییرات انرژی پتانسیل برابر با کار انجام شده در خازن است، یعنی داریم:

$$\large -\Delta U=W$$

و بدین ترتیب به رابطه‌ای مشابه برای کار خازن در ولتاژ ثابت خواهیم رسید. در یک خازن تمام پارامترهای لازم را برای انجام کار مکانیکی موجود است.

خازن باید چرخه نشان داده شده در شکل (۲) را دنبال کند. شباهت این چرخه با چرخه‌های ترمودینامیکی موتورهای حرارتی منجر به استفاده از اصطلاحاتی همچون انبساط یا فشرده کردن می‌شود که از این اصطلاحات معمولاً برای گازها استفاده می‌شود.

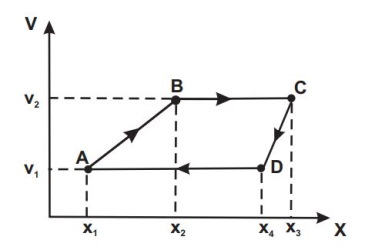
خازن از حالت A با مختصات $$(x_{1},V_{1})$$ شروع می‌شود و با بار ثابت به حالت B با مختصات $$(x_{2},V_{2})$$ می‌رسد. سپس در ولتاژ ثابت از B با مختصات $$(x_{2},V_{2})$$ به نقطه C با مختصات $$(x_{3},V_{2})$$ می‌رود. در مرحله بعد از نقطه C در حالت بار الکتریکی ثابت به نقطه D با مختصات $$(x_{4},V_{1})$$ می‌رسد. در مرحله آخر این چرخه سیستم دوباره به نقطه A با مختصات $$(x_{1},V_{1})$$ می‌رسد.

در این مرحله می‌توانیم کار مکانیکی در هر مرحله را که توسط خازن انجام می‌شود محاسبه کنیم و کار کل خازن برابر با مجموع این کارها در یک چرخه کامل است.

• از A تا B کار در حالی که بار الکتریکی ثابت است برابر است با:

$$\large W_{A,B} =\frac{\epsilon_{0}AV_1^2}{2x_1^2}(x_{2}-x_{1})$$

• از B تا C سیستم در ولتاژ ثابت است و طبق آن کار روی سیستم برابر است با:

$$\large W_{B,C}=\frac{\epsilon_{0}AV_{2}^{2}}{2}(\frac{1}{x_{2}}-\frac{1}{x_{3}})$$

• در فرآیند صورت گرفته بین C به D بار ثابت است و با استفاده از رابطه کار در بار ثابت داریم:

$$\large W_{C,D} =\frac{\epsilon_{0}AV_1^2}{2x_3^2}(x_{4}-x_{3})$$

• در نهایت از D به A کار انجام شده در ولتاژ ثابت برابر است با:

$$\large W_{D,A}=\frac{\epsilon_{0}AV_{1}^{2}}{2}(\frac{1}{x_{4}}-\frac{1}{x_{1}})$$

بدین ترتیب کار خالص روی سیستم برابر با مجموع کار انجام شده در هر مرحله است و داریم:

$$\large W_{net} =\epsilon_{0}A(\frac{V_1}{x_1}-\frac{V_2}{x_3})(V_{2}-V_{1})$$

در معادله بالا از تناسب‌های بین ولتاژ و $$x$$ استفاده کردیم. همان‌طور که پیش‌تر نشان دادیم:

$$\large x_{2} =\frac{x_{1}V_2}{V_1}$$

$$\large x_{4} =\frac{x_{3}V_1}{V_2}$$

کار خالص در یک چرخه که به دست آوردیم نشان می‌دهد که کار حالص یک خازن در یک چرخه بسته غیر صفر است. اگر نمودار بار‌ الکتریکی بر حسب ولتاژ را رسم کنیم، نموداری به صورت زیر خواهیم داشت:

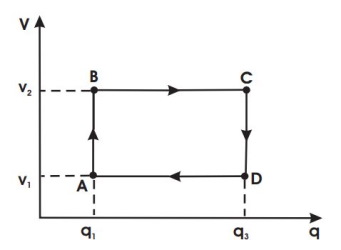
در این فضا نمودار چرخه به صورت یک مستطیل است و محاسبه فضای محصور شده آسان است و داریم:

$$\large q_1=C_1V_1=\frac{\epsilon_0A}{x_1}V_1$$
$$\large q_3=C_3V_3=C_3V_2=\frac{\epsilon_0A}{x_1}V_1$$

در نتیجه مساحت مستطیل برابر است با:

$$\large Area =\epsilon_{0}A(\frac{V_2}{x_3}-\frac{V_1}{x_1})(V_{2}-V_{1})$$

مساحت محصور در مستطیل کار خالصی است که توسط سیستم ضربدر یک علامت منفی انجام می‌شود.

اگر بخواهیم شرایط را به حالت واقع بینانه‌تر نزدیک کنیم بهتر است که مقاومت سیم را نیز در نظر گرفته و گرمای منتشر شده را نیز محاسبه کنیم. با این وجود ارزیابی این حالت به دلیل تغییر جریان الکتریکی بین باتری و خازن دشوار است زیرا ظرفیت خازن با تغییر فاصله صفحات خازن تغییر می‌کند. برای محاسبه تغییرات ظرفیت خازن بر حسب فاصله بین صفحات خازن باید بدانیم که این تغییرات با چه آهنگی صورت می‌گیرد، در حقیقت باید معادله مربوط به $$x(t)$$ را بدانیم.

به طور خلاصه ممکن است یک موتور الکتریکی از دو باتری با پتانسیل $$V_1$$ و $$V_2$$ و یک خازن ساخته شده باشد.

مثال کار خازن

مثال: یک خازن با ظرفیت C که در ابتدا بدون بار است به یک باتری متصل می‌شود. گرمای پخش شده در مدار را در حین باردار شدن خازن به دست آورید.

فیلم آموزش فیزیک عمومی 2 – حل مساله در فرادرس

کلیک کنید

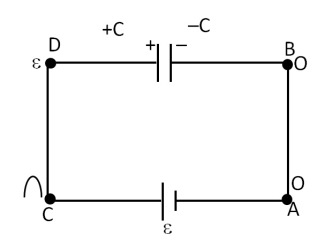
پاسخ: فرض کنید پتانسیل در نقطه A صفر است، در نتیجه در نقطه B نیز پتانسیل صفر است و در نقاط C و D پتانسیل برابر با $$\epsilon$$ است. همچنین ظرفیت خازن برابر است با:

$$\large Q=\epsilon C$$

می‌دانیم نیروی محرکه یک باتری برابر است با:

$$\large \epsilon=\frac{dW}{dq}$$

این رابطه انرژی لازم در یک باتری را برای جابه‌جایی بار الکتریکی فراهم می‌کند. در نتیجه کار انجام شده توسط باتری برابر است با:

$$\large dW=\epsilon\ dq$$

از طرفی می‌دانیم $$dq=I dt$$، در نتیجه داریم:

$$\large W= \int \epsilon I\ dt$$
$$\large \Rightarrow \int \epsilon I\ dt= \int qC\times \frac{dq}{dt}\times dt$$
$$\large \rightarrow C\int_0^Q qdq=\frac{Q^{2}}{2C}$$
$$\large W=\frac{\epsilon^{2}C}{2}$$

در نتیجه می‌توان گرمای پخش شده در مدار را به دست آورد که با پتانسیل دو سر باتری و ظرفیت خازن متناسب است.