چرخ دنده مخروطی – از صفر تا صد

قبلاً در مقاله چرخ دنده - به زبان ساده، به معرفی انواع پرکاربرد چرخ دنده در صنعت پرداختیم. یکی از انواع چرخ دنده‌ها، چرخ دنده مخروطی است که وظیفه انتقال نیرو بین دو محور متقاطع را به عهده دارد. همان‌طور که قبلاً هم گفتیم، دندانه‌های این چرخدنده می‌تواند مستقیم، مارپیچ یا هیپوئیدی باشد. روش‌های ساخت این چرخ دنده با دندانه مستقیم در حال منسوخ شدن است. همچنین از طرف دیگر، این نوع دندانه‌ها در هنگام درگیر شدن، سر و صدای زیادی ایجاد می‌کنند. همین دو عامل کافیست تا موجب محبوبیت دندانه‌های مارپیچ در آینده‌ای نزدیک شود. غیر از نوع دندانه، چرخ دنده‌ها را می‌توان براساس گام دندانه، تکنیک ساخت، صیقل دادن یا ندادن، جنس چرخ دنده و غیره دسته‌بندی کرد. چرخ دنده مخروطی، عموماً در محل تقاطع محورها به کار می‌رود. از آنجایی که نوع درگیر شدن این چرخ دنده، از نوع تماس غلتشی است، راندمان آن بالا و در بازه $$\large 93$$ تا $$\large 99$$ درصد خواهد بود. در شکل زیر، کاربرد چرخ دنده مخروطی در یک نمونه‌ آسیاب قدیمی نشان داده شده است.

چرخ دنده مخروطی با دندانه مستقیم

چرخ دنده‌های مخروطی، ظاهری مخروطی شکل دارند و برای انتقال نیرو بین دو محور متقاطع به کار می‌روند. ساده‌ترین نوع این چرخ دنده، دندانه مستقیم دارد. امتداد این دندانه‌ها به رأس مخروط فرضی می‌رسد. فرآیند ساخت این دندانه‌ها راحت‌تر است و هیچ نیروی تراستی هم ایجاد نمی‌کنند. در سوی مقابل، نقطه ضعف این نوع دندانه‌ها این است که بعد از گرم‌کاری، امکان سنگ زدن دندانه‌ها وجود ندارد. دندانه‌های مستقیم به دو روش «گلیسون» (Gleason) و استاندارد ساخته می‌شود. در روش گلیسون، انتهای دندانه‌ها دارای انحنایی به سمت داخل است. حتی اگر اشتباه‌های کوچکی در تراز بودن محورها هم رخ داده باشد، این چرخ دنده‌ها قادر به تحمل آن هستند. دندانه‌های مستقیم، معمولاً در کاربردهایی با سرعت پایین (کمتر از دو متر بر ثانیه سرعت محیطی) مورد استفاده قرار می‌گیرند. کاربرد اصلی آنها در ماشین ابزار، دستگاه چاپ و دیفرانسیل خودرو است. همچنین برای انتقال نیروهای بزرگ، به ندرت به کار می‌روند.

فیلم آموزش شبیه سازی حرکتی - چرخ دنده مخروطی در کتیا (رایگان) در فرادرس

کلیک کنید

چرخ دنده مخروطی با دندانه مارپیچ

دندانه‌های این نوع چرخ دنده به صورت منحنی‌های مارپیچ هستند. برخلاف نوع مستقیم، این دندانه‌ها به صورت آرام آرام و یکنواخت با هم درگیر می‌شوند. از هر دو روش ساخت گلیسون و استاندارد در این مدل هم استفاده می‌شود. ولی نوع گلیسون، کاربرد بیشتری دارد. در این نوع چرخ دنده‌ها، امکان سنگ زدن دندانه‌ها بعد از گرم‌کاری وجود دارد. همین امر، امکان تولید چرخ دنده‌های دقیق‌تری را فراهم می‌سازد.

نسبت تماس دندانه در این مدل نسبت به دندانه مستقیم بیشتر است. در نتیجه نویز و ارتعاش کمتری ایجاد می‌شود. از این رو، این نوع چرخ دنده در کاربردهایی با سرعت بالاتر مناسب است. از طرف دیگر، قدرت تحمل بار هم در این نوع چرخ دنده بیشتر است. اما در سوی مقابل، ساخت این نوع دندانه‌ها دشوارتر از نوع مستقیم است. همچنین باید به جهت نیروی تراست و وابستگی آن به چرخش و زاویه پیچش، توجه زیادی کرد. کاربرد این چرخ دنده‌ها عموماً برای کاهش سرعت و در ماشین‌های ابزار است.

پارامترهای هندسی چرخ دنده مخروطی

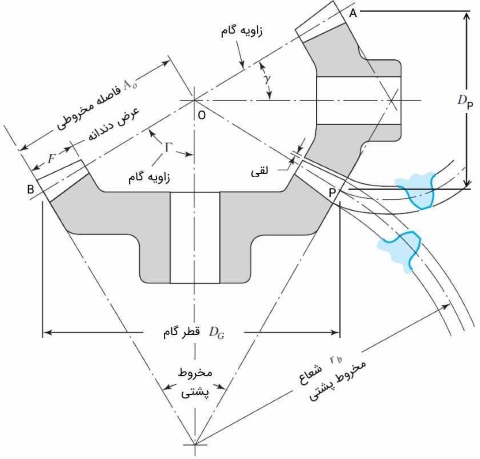
پارامترهای هندسی چرخ دنده مخروطی در شکل زیر نشان داده شده‌اند. بسیاری از پارامترهایی که در چرخ دنده ساده مطرح هستند، در اینجا به شکلی متفاوت به چشم می‌خورند. گام چرخ دنده در لبه بزرگتر اندازه‌گیری می‌شود. قطر گام مانند چرخ دنده ساده محاسبه می‌شود و لقی، یکنواخت است. زاویه گام را می‌توان مطابق رابطه‌های زیر و با استفاده از تعداد دندانه‌ها به دست آورد. تعداد دندانهای پینیون با $$N_P$$ و تعداد دندانه‌های چرخ دنده با $$N_G$$ بیان شده است.

$$\large \tan\gamma = \frac{N_P}{N_G}\\~\\ \large \tan \Gamma= \frac{N_G}{N_P}$$

تصویر بالا نشان می‌دهد وقتی دندانه‌های چرخ دنده مخروطی روی محیط مخروط پشتی تصویر شود، ظاهری شبیه دندانه‌های چرخ دنده ساده دارد. مطابق این فرضیه که «ترِدگلد» (TredGold) نامیده می‌شود، تعداد دندانه‌های چرخ دنده فرضی از رابطه زیر به دست می‌آید. شعاع مخروط پشتی را با $$r_b$$ نشان داده‌ایم. در واقع، کار با پروفایل واقعی دندانه دشوار است. زیرا دندانه‌ها روی سطح کروی قرار گرفته‌اند. به همین دلیل، از چنین تقریبی استفاده می‌کنیم.

$$\large N^\prime=\frac{2\pi r_b}{p}$$

در شکل قبل، برشی از یک جفت چرخ دنده مخروطی نشان داده شده است. خطوط $$\large AOP$$ و $$\large BOP$$ مخروط‌های گام هستند. برای اینکه در تمام مسیر خط $$\large OP$$ حرکت غلتشی داشته باشیم، مخروط‌ها باید دارای رأس مشترک $$\large O$$ باشند. متداول‌ترین زاویه بین محور دو مخروط، ۹۰ درجه است. قطرهای گام با $$\large D_G$$ و $$\large D_P$$ نشان داده شده‌اند و با قطر مخروط‌های گام در لبه بزرگ‌تر برابرند. گام دایره‌ای $$\large p$$، مدول $$\large m$$ و گام قطری $$\large P$$ در چرخ دنده مخروطی، همانند چرخ دنده ساده و به طریق زیر به دست می‌آیند.

$$\large p = \frac {\pi D}{N}, ~~~ m \ \frac {D}{N}, ~~~ p=\pi m, ~~~ P=\frac {N}{D}, ~~~ pP=\pi$$

همچنین، بین سرعت‌های زاویه‌ای و قطرهای گام نیز رابطه زیر برقرار است. معمولاً در انواع مختلف این نوع چرخ دنده، نسبت سرعت، بین $$\large 3:2$$ و $$\large 5:1$$ است.

$$\large \frac {\omega_G}{\omega_P} = \frac {D_P}{D_G} = \frac {N_P}{N_G}$$

محاسبه نیروها در چرخ دنده مخروطی

هنگام تعیین نیروهای وارد به محور و یاتاقان، از نیروی مماسی یا انتقالی استفاده می‌شود. وقتی تمام نیروها به وسط دندانه وارد شود، می‌توان از این فرض استفاده کرد. اما در واقعیت، برآیند نیروها در نقطه‌ای بین وسط دندانه و لبه بزرگتر آن وارد می‌شود. که البته خطای ناچیزی ایجاد می‌کند. همانند چرخ دنده ساده، نیروی انتقالی با استفاده از رابطه زیر به دست می‌آید.

$$\large W_t=\frac{T}{r_{av}}$$

فیلم آموزش چرخ دنده ها در طراحی اجزا 2 - استراتژی حل مساله با حل نمونه سوال (رایگان) در فرادرس

کلیک کنید

در این رابطه، $$\large T$$ گشتاور و $$\large {r_{av}}$$ شعاع گام در نقطه وسط دندانه مورد نظر است. در شکل زیر، محل ورود نیروها را در وسط دندانه فرض کردیم. نیروی برآیند $$\large W$$ سه مولفه دارد: یکی در جهت مماسی که با $$W_t$$ نشان داده شده، دیگری $$W_r$$ که نیروی شعاعی است و بالاخره $$W_a$$ که در راستای محوری وارد می‌شود. با توجه به زاویه‌های مشخص شده در شکل، رابطه‌های زیر برقرار است.

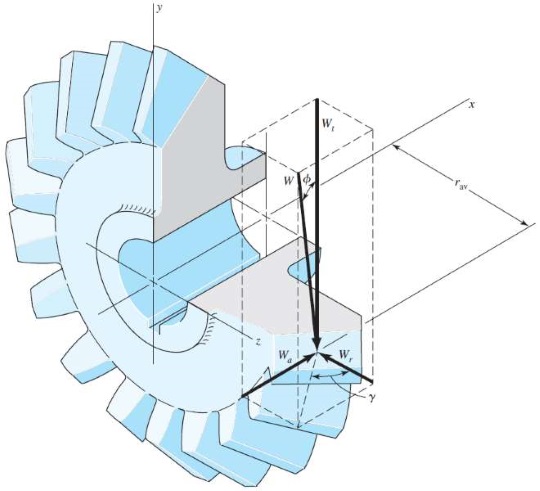
$$\large W_r=W_t\tan\phi\:\cos\gamma\\~\\ \large W_a=W_t\tan\phi\:\sin\gamma$$

مثال

سؤال: پینیون مخروطی شکل زیر با $$\large 15$$ دندانه و سرعت $$600\:rev/min$$ در جهت نشان داده شده در حال چرخش است. در نتیجه این چرخش، توان $$\large 5$$ اسب بخار به چرخ دنده‌ای با $$\large 45$$ دندانه منتقل می‌شود. اندازه‌های مختلف روی تصویر مشخص شده و اندازه‌ها به اینچ است. نیروی تراست وارد به یاتاقان‌های $$A$$ و $$B$$ را بیابید.

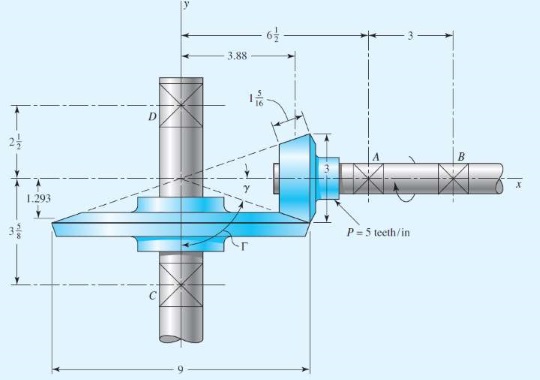
پاسخ: ابتدا زاویه‌های گام را محاسبه می‌کنیم.

$$\large \gamma = \tan^{-1}(\frac{3}{9})=18.4^\circ~~~~~ \Gamma = \tan^{-1}(\frac{9}{3})=71.6^\circ$$

فیلم آموزش استراتژی حل مساله در طراحی اجزای ماشین 1 در فرادرس

کلیک کنید

برای به دست آوردن سرعت خطی متناظر با شعاع متوسط دایره گام، به شیوه زیر عمل می‌کنیم.

$$\large V= \frac{2\pi r_pn}{12}=\frac{2 \pi (1.293)(600)}{12}=406\:ft/min$$

در نتیجه، نیروی انتقالی با کمک رابطه زیر به دست می‌آید.

$$\large W_t=\frac{33000\times H}{V} =\frac{33000\times 5}{406} =406\:lbf$$

با استفاده از رابطه‌هایی که در متن مقاله به دست آمد، نیروهای شعاعی و محوری به صورت زیر محاسبه می‌شوند.

$$\large W_r= W_t\tan\phi\:\cos\Gamma =406\tan20^\circ\:\cos71.6^\circ=46.6\:lbf\\~\\ \large W_a= W_t\tan\phi\:\sin\Gamma =406\tan20^\circ\:\sin71.6^\circ=140\:lbf$$

در اینجا $$W_t$$ در جهت مثبت $$z$$، $$W_r$$ در جهت منفی $$x$$ و $$W_a$$ در جهت منفی $$y$$ وارد شده است. جهت این نیروها را در شکل زیر مشاهده می‌کنید. در این شکل نمودار جسم آزاد سیستم رسم شده است.

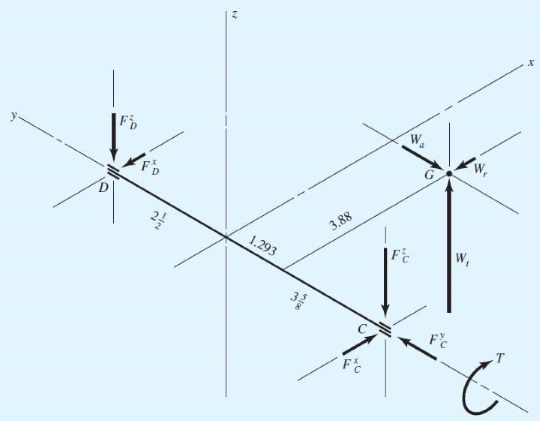
برآیند گشتاورها را حول نقطه $$D$$ نوشته و برابر صفر قرار می‌دهیم.

$$\large R_G=3.88i-(2.5+1.293)j=3.88i-3.793j\\~\\ \large R_C=-(2.5+3.625)j=-6.125j\\~\\ \large R_G\times W +R_C\times F_C + T=0\\~\\ \large F_C = F_C^xi +F_C^yj +F_C^zk\\~\\ \large (3.88i-3.793j)\times(-46.6i -140j +406k)\\ \large +(-6.125j)\times(F_C^xi +F_C^yj +F_C^zk)+Tj=0\\~\\ \large (-1540i -1575j -720k) + (-6.125\:F_C^zi + 6.125F_C^xk) + Tj = 0\\~\\ \large \Rightarrow \begin{cases}T=1575j\:lbf.in \\F_C^x=118\:lbf \\F_C^z=-251\:lbf \end{cases}$$

اکنون مطابق قوانین استاتیک، برآیند نیروها را برابر صفر قرار می‌دهیم.

$$\large F_D + F_C +W=0\\~\\ \large (F_D^x\:i\:+F_D^x\:k)+(118\:i\:+F_C^y\:j\:-251\:k)+(-46.6\:i\:-140\:j\:+406\:k)=0\\~\\ \large \Rightarrow\begin{cases} F_C=118\:i\:+140\:j\:-251\:k\:\:lbf \\ F_D=-71.4\:i\:-155\:k\:\:lbf \end{cases}$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزش‌های زیر نیز پیشنهاد می‌شوند:

• چرخ دنده – به زبان ساده
• چرخ دنده حلزونی – از صفر تا صد
• نسبت چرخ دنده — به زبان ساده
• حرکت دایره ای – به زبان ساده

^^